numpy.random.Generator.gumbel

метод

random.Generator.Гумбеля(loc=0.0, scale=1.0, размер=None)

Генерировать выборки из распределения Гумбеля.

Извлечение выборок из распределения Гумбеля с указанным положением и масштабом. Для получения дополнительной информации о распределении Гумбеля см. Примечания и Ссылки ниже.

Параметры:

locfloat или array_like из floats, необязательный

Расположение моды распределения. По умолчанию равно 0.

scalefloat или array_like из floats, необязательный

Параметр масштаба распределения. По умолчанию равен 1. Должен быть неотрицательным.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если loc и scale оба являются скалярами. В противном случае, np.broadcast(loc, scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные выборки из параметризованного распределения Гумбеля.

Смотрите также

scipy.stats.gumbel_l

scipy.stats.gumbel_r

scipy.stats.genextreme

weibull

Примечания

Распределение Гумбеля (или Наименьшее Экстремальное Значение (SEV) или Наименьшее Экстремальное Значение Типа I) является одним из класса Обобщенных Экстремальных Значений (GEV) распределений, используемых при моделировании задач экстремальных значений. Гумбель — это частный случай распределения Экстремального Значения Типа I для максимумов из распределений с «экспоненциально-подобными» хвостами.

Плотность вероятности для распределения Гумбеля равна

\[p(x) = \frac{e^{-(x - \mu)/ \beta}}{\beta} e^{ -e^{-(x - \mu)/ \beta}},\]

где \(\mu\) это мода, параметр положения, и \(\beta\) является параметром масштаба.

Распределение Гумбеля (названо в честь немецкого математика Эмиля Юлиуса Гумбеля) использовалось очень рано в гидрологической литературе для моделирования возникновения паводковых событий. Оно также используется для моделирования максимальной скорости ветра и интенсивности осадков. Это распределение с 'тяжелыми хвостами' — вероятность события в хвосте распределения больше, чем если бы использовалось гауссово распределение, отсюда удивительно частое возникновение 100-летних паводков. Паводки изначально моделировались как гауссов процесс, который недооценивал частоту экстремальных событий.

Это один из класса распределений экстремальных значений, обобщенных распределений экстремальных значений (GEV), который также включает Вейбулла и Фреше.

Функция имеет среднее значение \(\mu + 0.57721\beta\) и дисперсия \(\frac{\pi^2}{6}\beta^2\).

Ссылки

[1]

Гумбель, Э. Дж., «Статистика экстремальных значений», Нью-Йорк: Издательство Колумбийского университета, 1958.

[2]

Райсс, Р.-Д. и Томас, М., "Статистический анализ экстремальных значений из страхования, финансов, гидрологии и других областей", Базель: Birkhauser Verlag, 2001.

Примеры

Попробуйте в вашем браузере!

Извлечь выборки из распределения:

>>> rng = np.random.default_rng()
>>> mu, beta = 0, 0.1 # location and scale
>>> s = rng.gumbel(mu, beta, 1000)

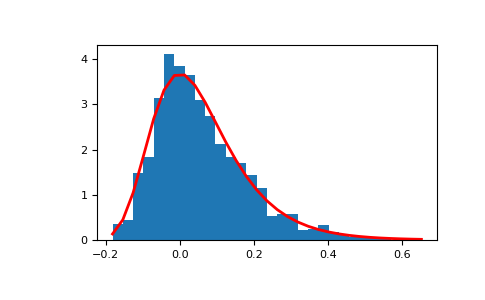
Отображение гистограммы выборок вместе с функцией плотности вероятности:

>>> import matplotlib.pyplot as plt
>>> count, bins, _ = plt.hist(s, 30, density=True)
>>> plt.plot(bins, (1/beta)*np.exp(-(bins - mu)/beta)
...          * np.exp( -np.exp( -(bins - mu) /beta) ),
...          linewidth=2, color='r')
>>> plt.show()

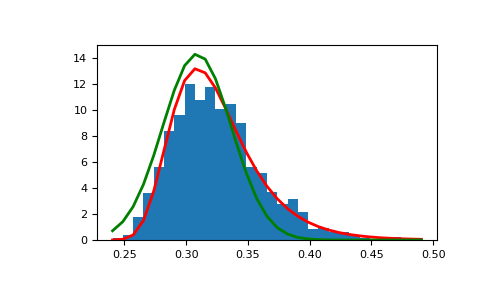
Показать, как распределение экстремальных значений может возникнуть из гауссовского процесса и сравнить с гауссовским:

>>> means = []
>>> maxima = []
>>> for i in range(0,1000) :
...    a = rng.normal(mu, beta, 1000)
...    means.append(a.mean())
...    maxima.append(a.max())
>>> count, bins, _ = plt.hist(maxima, 30, density=True)
>>> beta = np.std(maxima) * np.sqrt(6) / np.pi
>>> mu = np.mean(maxima) - 0.57721*beta
>>> plt.plot(bins, (1/beta)*np.exp(-(bins - mu)/beta)
...          * np.exp(-np.exp(-(bins - mu)/beta)),
...          linewidth=2, color='r')
>>> plt.plot(bins, 1/(beta * np.sqrt(2 * np.pi))
...          * np.exp(-(bins - mu)**2 / (2 * beta**2)),
...          linewidth=2, color='g')
>>> plt.show()

НазадОткрыть во вкладке