numpy.random.Generator.wald#

метод

random.Generator.wald(mean, scale, размер=None)#

Генерация выборок из распределения Вальда или обратного гауссовского распределения.

По мере приближения масштаба к бесконечности распределение становится более похожим на гауссово. Некоторые источники утверждают, что распределение Вальда является обратным гауссовым со средним, равным 1, но это отнюдь не универсально.

Обратное распределение Гаусса впервые было изучено в связи с броуновским движением. В 1956 году М.К.К. Твиди использовал название обратное Гауссово, потому что существует обратная зависимость между временем покрытия единичного расстояния и расстоянием, покрытым за единицу времени.

Параметры:
meanfloat или array_like из float

Среднее распределения, должно быть > 0.

scalefloat или array_like из float

Параметр масштаба, должен быть > 0.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если mean и scale оба являются скалярами. В противном случае, np.broadcast(mean, scale).size выбираются образцы.

Возвращает:
выходndarray или скаляр

Выбранные образцы из параметризованного распределения Вальда.

Примечания

Функция плотности вероятности для распределения Вальда

\[P(x;mean,scale) = \sqrt{\frac{scale}{2\pi x^3}}e^ \frac{-scale(x-mean)^2}{2\cdotp mean^2x}\]

Как отмечалось выше, обратное распределение Гаусса впервые возникло из попыток моделирования броуновского движения. Оно также является конкурентом распределению Вейбулла для использования в моделировании надежности, моделировании доходности акций и процессов процентных ставок.

Ссылки

[2]

Чхикара, Радж С., и Фолкс, Дж. Лерой, «Обратное гауссовское распределение: теория, методология и приложения», CRC Press, 1988.

[3]

Википедия, "Обратное гауссовское распределение" https://en.wikipedia.org/wiki/Inverse_Gaussian_distribution

Примеры

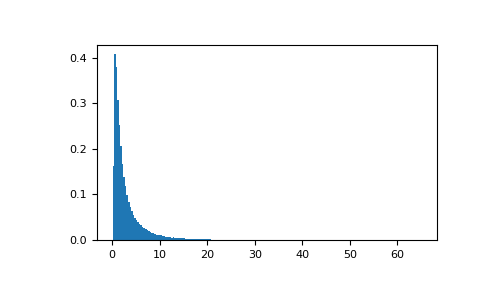
Извлечь значения из распределения и построить гистограмму:

>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> h = plt.hist(rng.wald(3, 2, 100000), bins=200, density=True)
>>> plt.show()
../../../_images/numpy-random-Generator-wald-1.png
На этой странице