numpy.random.Generator.exponential

метод

random.Generator.экспоненциальный(scale=1.0, размер=None)

Извлечение выборок из экспоненциального распределения.

Его функция плотности вероятности

\[f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta}),\]

для x > 0 и 0 в других местах. \(\beta\) является параметром масштаба, который является обратным параметру скорости \(\lambda = 1/\beta\). Параметр rate является альтернативной, широко используемой параметризацией экспоненциального распределения [3].

Экспоненциальное распределение является непрерывным аналогом геометрического распределения. Оно описывает многие распространенные ситуации, такие как размер капель дождя, измеренный во многих дождях [1], или время между запросами страниц в Википедии [2].

Параметры:

scalefloat или array_like из float

Параметр масштаба, \(\beta = 1/\lambda\). Должно быть неотрицательным.

размерint или кортеж ints, опционально

Форма вывода. Если заданная форма, например, (m, n, k), затем m * n * k образцы извлекаются. Если size равен None (по умолчанию), возвращается единственное значение, если scale является скаляром. В противном случае, np.array(scale).size выбираются образцы.

Возвращает:

выходndarray или скаляр

Выбранные выборки из параметризованного экспоненциального распределения.

Ссылки

[1]

Пейтон З. Пиблс мл., «Вероятность, случайные величины и принципы случайных сигналов», 4-е изд., 2001, стр. 57.

[2]

Википедия, «Пуассоновский процесс», https://en.wikipedia.org/wiki/Poisson_process

[3]

Википедия, «Экспоненциальное распределение», https://en.wikipedia.org/wiki/Exponential_distribution

Примеры

Попробуйте в вашем браузере!

Предположим, что компания имеет 10000 агентов поддержки клиентов, а время между звонками клиентов распределено экспоненциально, и среднее время между звонками клиентов составляет 4 минуты.

>>> scale, size = 4, 10000
>>> rng = np.random.default_rng()
>>> time_between_calls = rng.exponential(scale=scale, size=size)

Какова вероятность того, что клиент позвонит в следующие 4-5 минут?

>>> x = ((time_between_calls < 5).sum())/size
>>> y = ((time_between_calls < 4).sum())/size
>>> x - y
0.08  # may vary

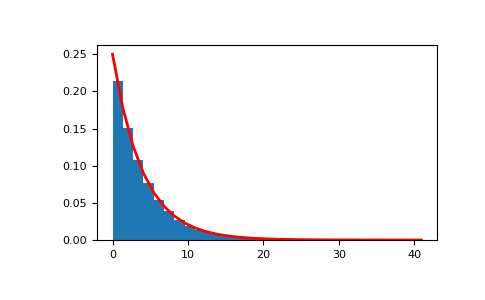
Соответствующее распределение можно визуализировать следующим образом:

>>> import matplotlib.pyplot as plt
>>> scale, size = 4, 10000
>>> rng = np.random.default_rng()
>>> sample = rng.exponential(scale=scale, size=size)
>>> count, bins, _ = plt.hist(sample, 30, density=True)
>>> plt.plot(bins, scale**(-1)*np.exp(-scale**-1*bins), linewidth=2, color='r')
>>> plt.show()

НазадОткрыть во вкладке