2.9. Модели нейронных сетей (без учителя)#
2.9.1. Ограниченные машины Больцмана#
Ограниченные машины Больцмана (RBM) — это неконтролируемые нелинейные обучатели признаков, основанные на вероятностной модели. Признаки, извлечённые RBM или иерархией RBM, часто дают хорошие результаты при подаче в линейный классификатор, такой как линейный SVM или перцептрон.
Модель делает предположения относительно распределения входных данных. В настоящее время
scikit-learn предоставляет только BernoulliRBM, который предполагает, что входные данные являются либо двоичными значениями, либо значениями от 0 до 1, каждое из которых кодирует вероятность того, что конкретный признак будет включен.
реализует алгоритм многослойного перцептрона (MLP), который обучается с использованиемСтохастическое максимальное правдоподобие) предотвращает отклонение представлений далеко от входных данных, что позволяет им захватывать интересные закономерности, но делает модель менее полезной для небольших наборов данных и обычно не полезной для оценки плотности.
Метод стал популярным для инициализации глубоких нейронных сетей с весами независимых RBM. Этот метод известен как неконтролируемое предварительное обучение.

Примеры
2.9.1.1. Графическая модель и параметризация#
Графическая модель RBM - это полностью связный двудольный граф.
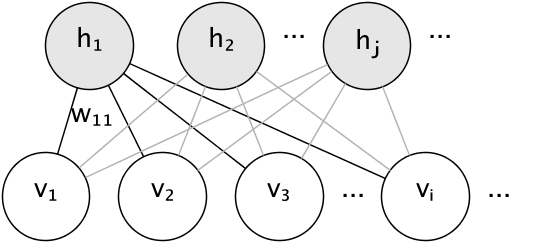
Узлы являются случайными величинами, состояния которых зависят от состояний других узлов, к которым они подключены. Модель параметризуется весами соединений, а также одним свободным членом (смещением) для каждого видимого и скрытого узла, опущенным на изображении для простоты.
Функция энергии измеряет качество совместного назначения:
В формуле выше, \(\mathbf{b}\) и \(\mathbf{c}\) являются векторами смещения для видимого и скрытого слоев соответственно. Совместная вероятность модели определяется через энергию:
Слово ограниченный относится к двудольной структуре модели, которая запрещает прямое взаимодействие между скрытыми единицами или между видимыми единицами. Это означает, что предполагаются следующие условные независимости:
Двудольная структура позволяет использовать эффективную блочную выборку Гиббса для вывода.
2.9.1.2. Машины Больцмана с ограничениями Бернулли#
В BernoulliRBM, все единицы являются бинарными стохастическими единицами. Это
означает, что входные данные должны быть либо бинарными, либо вещественными в диапазоне от 0 до
1, обозначающими вероятность включения или выключения видимой единицы. Это
хорошая модель для распознавания символов, где интерес представляет, какие
пиксели активны, а какие нет. Для изображений естественных сцен она больше не
подходит из-за фона, глубины и тенденции соседних пикселей принимать одинаковые значения.
Условное распределение вероятностей каждого узла задается логистической сигмоидальной функцией активации от получаемого входа:
где \(\sigma\) является логистической сигмоидной функцией:
2.9.1.3. Стохастическое обучение по методу максимального правдоподобия#
Алгоритм обучения, реализованный в BernoulliRBM известен как
Стохастическое максимальное правдоподобие (SML) или Персистентная контрастная дивергенция
(PCD). Оптимизация максимального правдоподобия напрямую неосуществима из-за
формы правдоподобия данных:
Для простоты уравнение выше записано для одного обучающего примера. Градиент по весам состоит из двух членов, соответствующих приведенным выше. Обычно они известны как положительный градиент и отрицательный градиент из-за их соответствующих знаков. В этой реализации градиенты оцениваются по мини-пакетам выборок.
При максимизации логарифма правдоподобия положительный градиент заставляет модель предпочитать скрытые состояния, совместимые с наблюдаемыми обучающими данными. Из-за двудольной структуры RBM это можно вычислить эффективно. Однако отрицательный градиент не поддается вычислению. Его цель — снизить энергию совместных состояний, которые предпочитает модель, тем самым заставляя ее оставаться верной данным. Его можно аппроксимировать методом Монте-Карло по цепи Маркова, используя блочную выборку Гиббса, итеративно выбирая каждый из \(v\) и \(h\) при условии другого, пока цепь не смешается. Сгенерированные таким образом выборки иногда называют фантазийными частицами. Это неэффективно, и трудно определить, смешивается ли цепь Маркова.
Метод контрастивной дивергенции предлагает остановить цепь после небольшого количества итераций, \(k\)Однако удаление одной категории нарушает симметрию исходного представления и поэтому может вызвать смещение в последующих моделях, например, для штрафованной линейной классификации или регрессионных моделей.
Устойчивое контрастное расхождение решает эту проблему. Вместо того чтобы запускать новую цепь каждый раз, когда требуется градиент, и выполнять только один шаг выборки Гиббса, в PCD мы сохраняем несколько цепей (фантазийные частицы), которые обновляются \(k\) шагов Гиббса после каждого обновления весов. Это позволяет частицам более тщательно исследовать пространство.
Ссылки
“A fast learning algorithm for deep belief nets”, Г. Хинтон, С. Осиндеро, Ю.-В. Те, 2006
“Обучение ограниченных машин Больцмана с использованием аппроксимаций градиента правдоподобия”, T. Tieleman, 2008