2.1. Гауссовские смеси моделей

sklearn.mixture — это пакет, который позволяет изучать Гауссовские смеси моделей (поддерживаются диагональные, сферические, связанные и полные ковариационные матрицы), выбирать их и оценивать их по данным. Также предоставляются средства для определения подходящего количества компонентов.

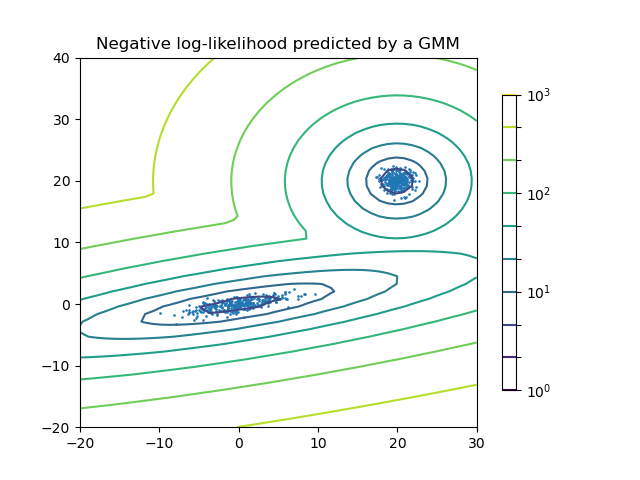
Двухкомпонентная гауссовская смесь: точек данных и поверхности равной вероятности модели.

Гауссова смесь — это вероятностная модель, которая предполагает, что все точки данных генерируются из смеси конечного числа гауссовых распределений с неизвестными параметрами. Можно рассматривать модели смесей как обобщение k-средних кластеризации, включающее информацию о ковариационной структуре данных, а также о центрах скрытых гауссовых распределений.

Scikit-learn реализует различные классы для оценки гауссовых смесей, которые соответствуют различным стратегиям оценки, подробно описанным ниже.

2.1.1. Гауссова смесь

The GaussianMixture объект реализует алгоритм максимизации ожидания (EM) алгоритм для подгонки моделей смеси Гауссов. Он также может рисовать доверительные эллипсоиды для многомерных моделей и вычислять байесовский информационный критерий для оценки количества кластеров в данных. A GaussianMixture.fit метод предоставляется, который обучает гауссову смесь моделей на обучающих данных. Для тестовых данных он может присвоить каждому образцу гауссову компоненту, к которой он, скорее всего, принадлежит, используя GaussianMixture.predict метод.

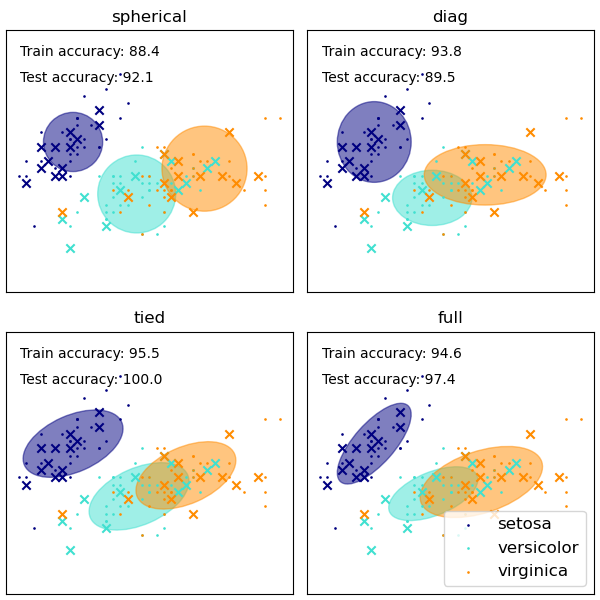
The GaussianMixture предоставляет различные варианты ограничения ковариации оценённых классов: сферическая, диагональная, связанная или полная ковариация.

Примеры

• См. Ковариации GMM для примера использования гауссовой смеси в качестве кластеризации на наборе данных iris.

• См. Оценка плотности для гауссовской смеси для примера построения оценки плотности.

Плюсы и минусы класса GaussianMixture

Преимущества

Скорость:

Это самый быстрый алгоритм для обучения смешанных моделей

Агностический:

Поскольку этот алгоритм максимизирует только правдоподобие, он не будет смещать средние значения к нулю или смещать размеры кластеров к определенным структурам, которые могут или не могут применяться.

Недостатки

Сингулярности:

Когда точек на смесь недостаточно, оценка ковариационных матриц становится сложной, и алгоритм может расходиться и находить решения с бесконечным правдоподобием, если не регуляризовать ковариации искусственно.

Количество компонент:

Этот алгоритм всегда будет использовать все компоненты, к которым у него есть доступ, требуя отложенные данные или информационно-теоретические критерии, чтобы решить, сколько компонентов использовать при отсутствии внешних сигналов.

Выбор количества компонент в классической модели гауссовской смеси

Критерий BIC может быть использован для эффективного выбора количества компонент в гауссовой смеси. Теоретически он восстанавливает истинное количество компонент только в асимптотическом режиме (т.е. если доступно много данных и предполагается, что данные фактически были сгенерированы независимо и одинаково распределены из смеси гауссовых распределений). Обратите внимание, что использование Вариационный байесовский гауссовский смесь избегает указания количества компонент для гауссовской смеси.

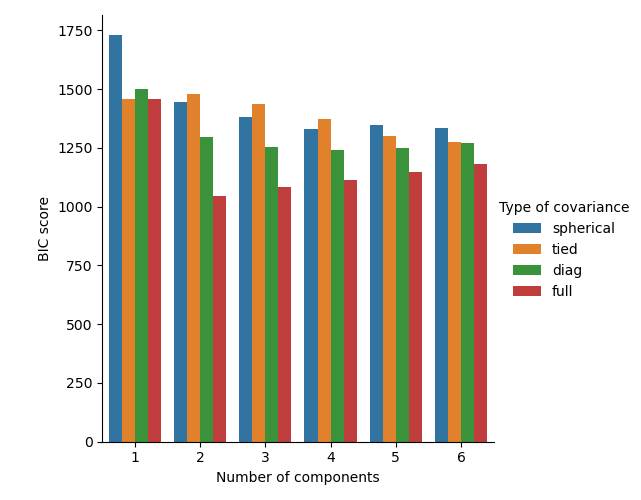
Примеры

• См. Выбор модели гауссовской смеси для примера выбора модели, выполненного с классической гауссовской смесью.

Алгоритм оценки: максимизация ожидания

Основная сложность в обучении моделей гауссовых смесей на немаркированных данных заключается в том, что обычно неизвестно, какие точки принадлежат какому латентному компоненту (если есть доступ к этой информации, становится очень легко подогнать отдельное гауссово распределение к каждому набору точек). Ожидание-максимизация является статистически обоснованным алгоритмом для обхода этой проблемы с помощью итеративного процесса. Сначала предполагаются случайные компоненты (случайно центрированные на точках данных, обученные с помощью k-means, или даже просто нормально распределенные вокруг начала координат) и вычисляется для каждой точки вероятность быть сгенерированной каждым компонентом модели. Затем параметры настраиваются для максимизации правдоподобия данных при этих назначениях. Повторение этого процесса гарантированно всегда сходится к локальному оптимуму.

Выбор метода инициализации

Существует выбор из четырех методов инициализации (а также возможность ввода пользовательских начальных средних) для генерации начальных центров компонентов модели:

k-means (по умолчанию)

Это применяет традиционный алгоритм кластеризации k-means. Это может быть вычислительно затратно по сравнению с другими методами инициализации.

k-means++

Это использует метод инициализации кластеризации k-means: k-means++. Первый центр выбирается случайным образом из данных. Последующие центры будут выбираться из взвешенного распределения данных, отдавая предпочтение точкам, находящимся дальше от существующих центров. k-means++ является методом инициализации по умолчанию для k-means, поэтому он будет быстрее, чем полный запуск k-means, но все же может занимать значительное количество времени для больших наборов данных со многими компонентами.

random_from_data

Это выберет случайные точки данных из входных данных в качестве начальных центров. Это очень быстрый метод инициализации, но может давать не сходящиеся результаты, если выбранные точки слишком близки друг к другу.

random

Центры выбираются как небольшое отклонение от среднего значения всех данных. Этот метод прост, но может привести к тому, что модель будет сходиться дольше.

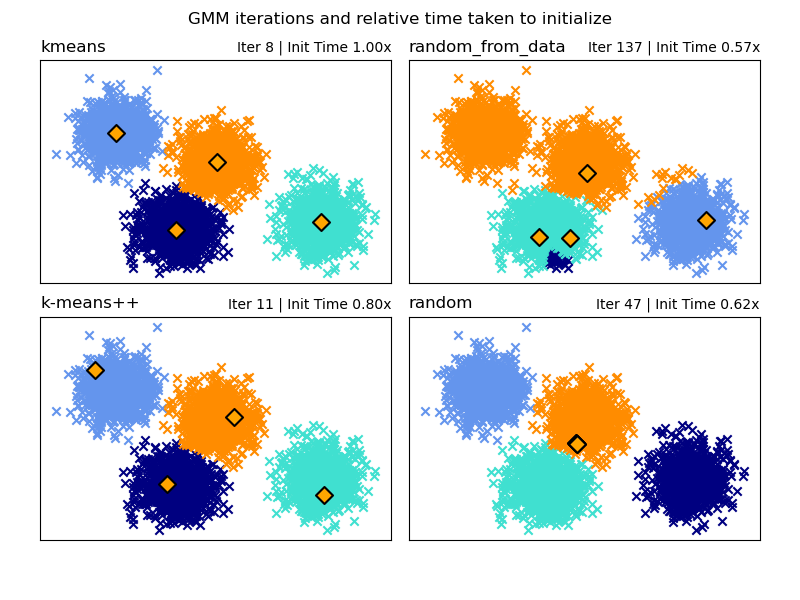
Примеры

• См. Методы инициализации GMM для примера использования различных инициализаций в гауссовской смеси.

2.1.2. Вариационный байесовский гауссовский смесь

The BayesianGaussianMixture объект реализует вариант гауссовской смеси с алгоритмами вариационного вывода. API похож на определённый GaussianMixture.

Алгоритм оценки: вариационный вывод

Вариационный вывод — это расширение алгоритма максимизации ожидания, которое максимизирует нижнюю границу для правдоподобия модели (включая априорные распределения) вместо правдоподобия данных. Принцип вариационных методов такой же, как у алгоритма максимизации ожидания (то есть оба являются итеративными алгоритмами, которые чередуют нахождение вероятностей для каждой точки быть сгенерированной каждой смесью и подгонку смеси к этим назначенным точкам), но вариационные методы добавляют регуляризацию, интегрируя информацию из априорных распределений. Это позволяет избежать сингулярностей, часто встречающихся в решениях алгоритма максимизации ожидания, но вносит некоторые тонкие смещения в модель. Вывод часто заметно медленнее, но обычно не настолько, чтобы сделать использование непрактичным.

Из-за байесовской природы вариационному алгоритму требуется больше гиперпараметров, чем алгоритму максимизации ожидания, наиболее важным из которых является параметр концентрации weight_concentration_prior. Указание низкого значения для априорной концентрации заставит модель распределить большую часть веса на несколько компонентов и установить веса оставшихся компонентов очень близкими к нулю. Высокие значения априорной концентрации позволят большему числу компонентов быть активными в смеси.

Реализация параметров BayesianGaussianMixture класс предлагает два типа априорного распределения для распределения весов: конечную смешанную модель с распределением Дирихле и бесконечную смешанную модель с процессом Дирихле. На практике алгоритм вывода процесса Дирихле аппроксимируется и использует усечённое распределение с фиксированным максимальным числом компонент (называемое представлением разбиения палки). Число фактически используемых компонент почти всегда зависит от данных.

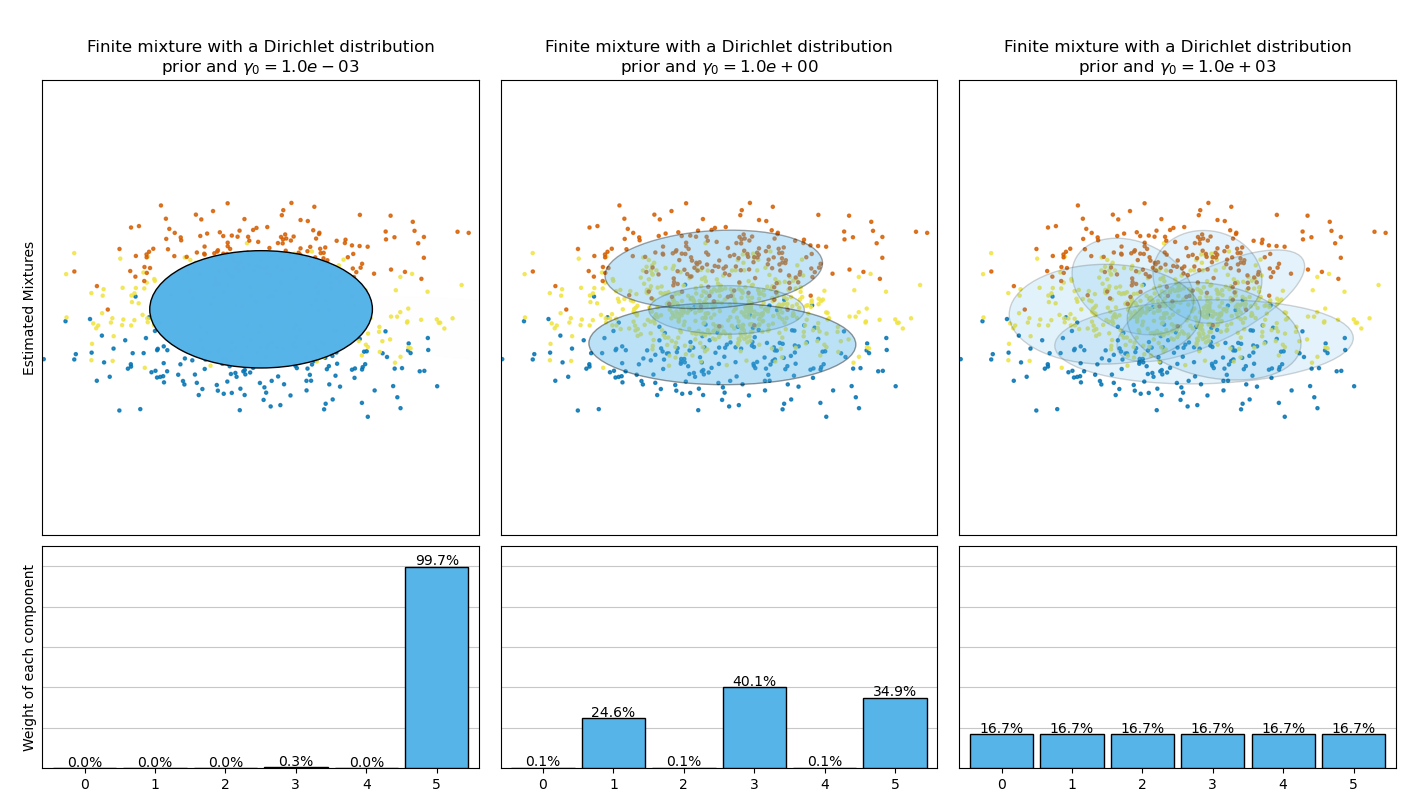
Следующий рисунок сравнивает результаты, полученные для различных типов априорного распределения концентрации весов (параметр weight_concentration_prior_type) для разных значений weight_concentration_prior. Здесь мы можем увидеть значение weight_concentration_prior параметр имеет сильное влияние на эффективное количество полученных активных компонентов. Мы также можем заметить, что большие значения для априорного веса концентрации приводят к более равномерным весам, когда тип априорного распределения - 'dirichlet_distribution', в то время как это не обязательно верно для типа 'dirichlet_process' (используемого по умолчанию).

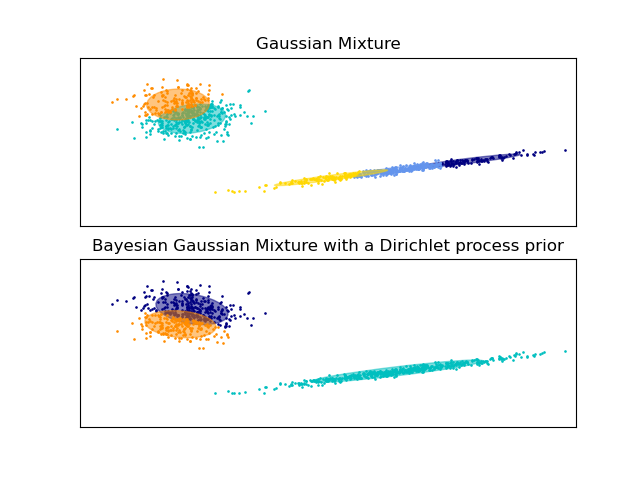
Примеры ниже сравнивают модели гауссовских смесей с фиксированным числом компонентов с вариационными моделями гауссовских смесей с априорным распределением Дирихле. Здесь классическая гауссовская смесь обучается с 5 компонентами на наборе данных, состоящем из 2 кластеров. Мы видим, что вариационная гауссовская смесь с априорным распределением Дирихле способна ограничиться только 2 компонентами, тогда как гауссовская смесь обучает данные с фиксированным числом компонентов, которое должно быть задано пользователем априори. В этом случае пользователь выбрал n_components=5 что не соответствует истинному генеративному распределению этого игрушечного набора данных. Обратите внимание, что при очень малом количестве наблюдений вариационные гауссовские смеси моделей с априорным распределением Дирихле могут занимать консервативную позицию и подгонять только одну компоненту.

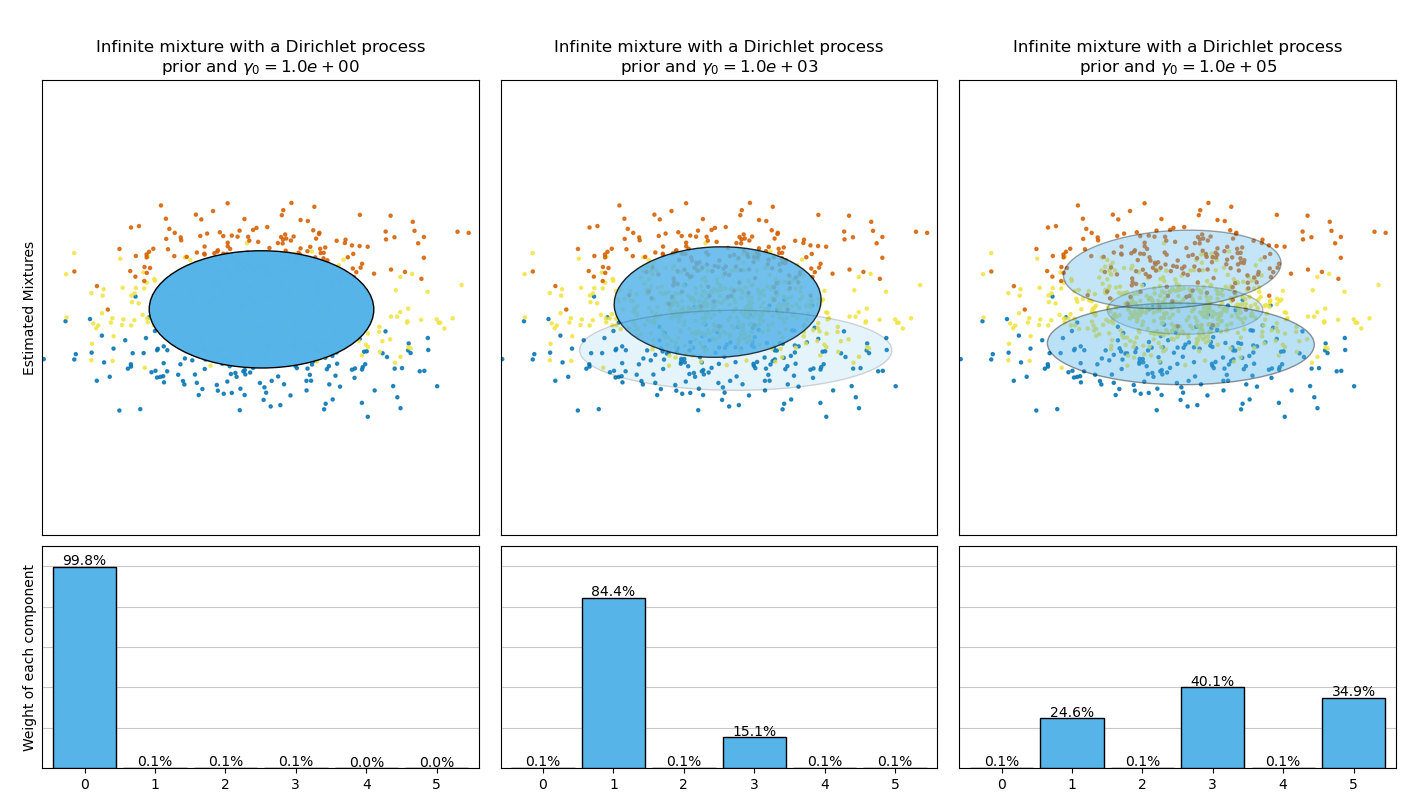
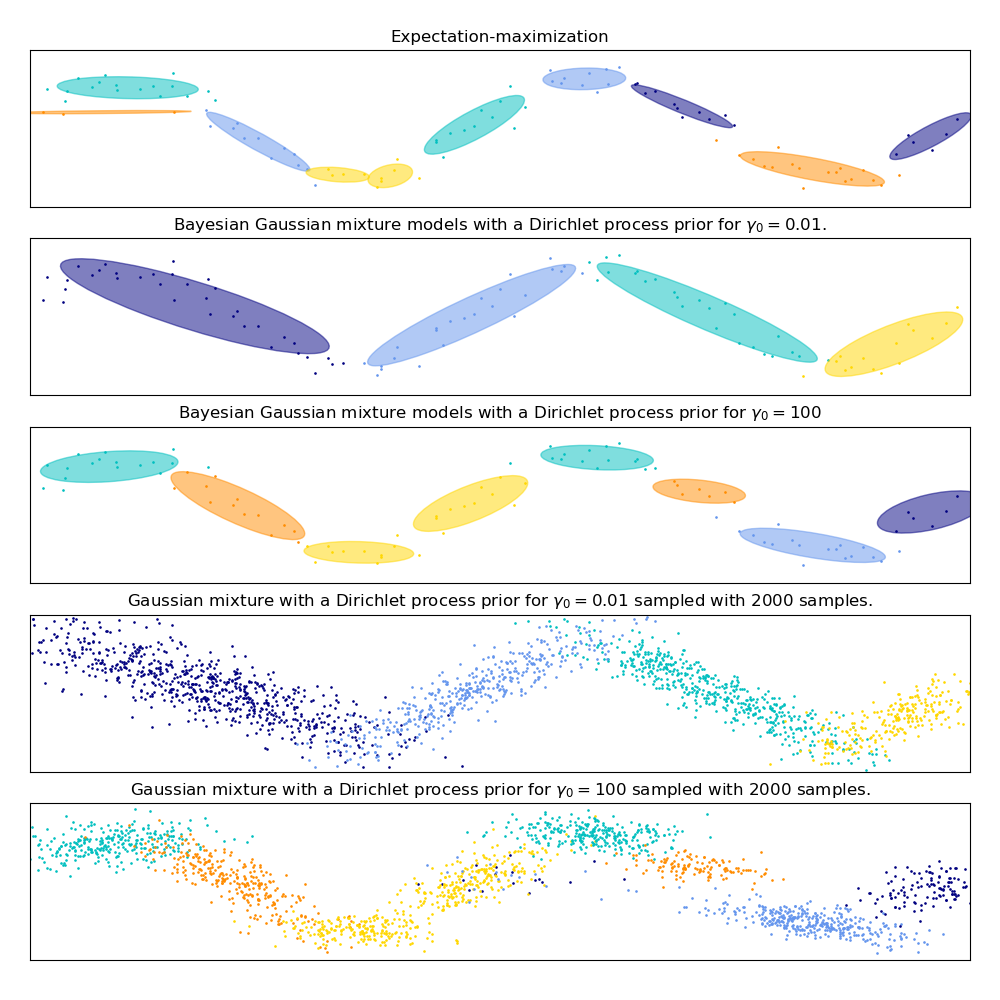
На следующем рисунке мы обучаем набор данных, который плохо описывается гауссовой смесью. Настройка weight_concentration_prior, параметр BayesianGaussianMixture управляет количеством компонентов, используемых для обучения этих данных. Мы также представляем на последних двух графиках случайную выборку, сгенерированную из двух полученных смесей.

Примеры

• См. Эллипсоиды гауссовской смеси для примера по построению доверительных эллипсоидов для обоих GaussianMixture и BayesianGaussianMixture.

• Гауссова смесь моделей синусоидальной кривой показывает использование GaussianMixture и BayesianGaussianMixture для подгонки синусоидальной волны.

• См. Анализ вариации байесовской гауссовой смеси с априорным типом концентрации для примера построения доверительных эллипсоидов для BayesianGaussianMixture с разными weight_concentration_prior_type для различных значений параметра weight_concentration_prior.

Преимущества и недостатки вариационного вывода с BayesianGaussianMixture

Преимущества

Автоматический выбор:

Когда weight_concentration_prior достаточно мал и n_components больше, чем необходимо модели, вариационная байесовская смесь моделей имеет естественную тенденцию устанавливать некоторые веса смеси близкими к нулю. Это позволяет модели автоматически выбирать подходящее количество эффективных компонентов. Требуется указать только верхнюю границу этого числа. Однако обратите внимание, что «идеальное» количество активных компонентов сильно зависит от конкретного приложения и обычно плохо определено в контексте исследования данных.

Меньшая чувствительность к количеству параметров:

В отличие от конечных моделей, которые почти всегда используют все компоненты настолько, насколько могут, и поэтому дают сильно различающиеся решения для разного количества компонентов, вариационный вывод с априорным распределением Дирихле (weight_concentration_prior_type='dirichlet_process') не сильно изменится при изменении параметров, что обеспечивает большую стабильность и требует меньше настройки.

Регуляризация:

Благодаря включению априорной информации, вариационные решения имеют менее патологические частные случаи, чем решения, полученные методом максимизации ожидания.

Недостатки

Скорость:

Дополнительная параметризация, необходимая для вариационного вывода, делает вывод медленнее, хотя и не намного.

Гиперпараметры:

Этому алгоритму нужен дополнительный гиперпараметр, который может потребовать экспериментальной настройки с помощью перекрестной проверки.

Смещение:

Существует много неявных смещений в алгоритмах вывода (а также в процессе Дирихле, если используется), и когда есть несоответствие между этими смещениями и данными, может быть возможно построить лучшие модели, используя конечную смесь.

2.1.2.1. Процесс Дирихле

Здесь мы описываем алгоритмы вариационного вывода для смеси Дирихле. Процесс Дирихле является априорным распределением вероятностей на кластеризации с бесконечным, неограниченным количеством разделовВариационные методы позволяют нам включать эту априорную структуру в модели гауссовских смесей практически без потерь во времени вывода по сравнению с конечной моделью гауссовской смеси.

Важный вопрос заключается в том, как процесс Дирихле может использовать бесконечное, неограниченное количество кластеров и при этом оставаться согласованным. Хотя полное объяснение не помещается в это руководство, можно думать о его процесс ломания палочки аналогия для помощи в понимании. Процесс ломания палочки - это генеративная история для процесса Дирихле. Мы начинаем с палочки единичной длины и на каждом шаге отламываем часть оставшейся палочки. Каждый раз мы связываем длину куска палочки с долей точек, попадающих в группу смеси. В конце, чтобы представить бесконечную смесь, мы связываем последний оставшийся кусок палочки с долей точек, которые не попадают во все другие группы. Длина каждого куска - случайная величина с вероятностью, пропорциональной параметру концентрации. Меньшие значения концентрации разделят единичную длину на более крупные куски палочки (определяя более концентрированное распределение). Большие значения концентрации создадут более мелкие куски палочки (увеличивая количество компонентов с ненулевыми весами).

Методы вариационного вывода для процесса Дирихле все еще работают с конечным приближением к этой бесконечной смесевой модели, но вместо необходимости заранее указывать, сколько компонентов нужно использовать, достаточно указать параметр концентрации и верхнюю границу на количество компонентов смеси (эта верхняя граница, предполагая, что она выше "истинного" количества компонентов, влияет только на алгоритмическую сложность, а не на фактическое количество используемых компонентов).