1.6. Ближайшие соседи

sklearn.neighbors предоставляет функциональность для неконтролируемых и контролируемых методов обучения на основе соседей. Неконтролируемые ближайшие соседи являются основой многих других методов обучения, особенно обучения многообразиям и спектральной кластеризации. Контролируемое обучение на основе соседей бывает двух видов: классификация для данных с дискретными метками, и регрессия для данных с непрерывными метками.

Принцип методов ближайших соседей заключается в нахождении предопределенного числа обучающих выборок, ближайших по расстоянию к новой точке, и предсказании метки на их основе. Количество выборок может быть задано пользователем константой (обучение методом k ближайших соседей) или варьироваться в зависимости от локальной плотности точек (обучение на основе радиуса соседей). Расстояние, как правило, может быть любой метрической мерой: стандартное евклидово расстояние является наиболее распространенным выбором. Методы на основе соседей известны как не обобщающие методы машинного обучения, поскольку они просто 'запоминают' все свои тренировочные данные (возможно, преобразованные в быструю структуру индексации, такую как Ball Tree или KD Tree).

Несмотря на свою простоту, метод ближайших соседей оказался успешным в большом количестве задач классификации и регрессии, включая распознавание рукописных цифр и сцен спутниковых изображений. Будучи непараметрическим методом, он часто успешен в ситуациях классификации, где граница решения очень нерегулярна.

Классы в sklearn.neighbors может обрабатывать либо массивы NumPy, либо scipy.sparse матрицы в качестве входных данных. Для плотных матриц поддерживается большое количество возможных метрик расстояния. Для разреженных матриц произвольные метрики Минковского поддерживаются для поиска.

Существует множество алгоритмов обучения, основанных на ближайших соседях. Один из примеров — оценка плотности ядра, обсуждается в оценка плотности раздел.

1.6.1. Неконтролируемые ближайшие соседи

NearestNeighbors реализует обучение ближайших соседей без учителя. Он действует как единый интерфейс к трем различным алгоритмам ближайших соседей: BallTree, KDTree, и алгоритм полного перебора, основанный на процедурах в sklearn.metrics.pairwise. Выбор алгоритма поиска соседей контролируется через ключевое слово 'algorithm', который должен быть одним из ['auto', 'ball_tree', 'kd_tree', 'brute']. Когда значение по умолчанию 'auto' передан, алгоритм пытается определить лучший подход на основе обучающих данных. Для обсуждения сильных и слабых сторон каждого варианта см. Алгоритмы ближайших соседей.

Предупреждение

Что касается алгоритмов ближайших соседей, если два соседа \(k+1\) и \(k\) имеют одинаковые расстояния, но разные метки, результат будет зависеть от порядка обучающих данных.

1.6.1.1. Поиск ближайших соседей

Для простой задачи поиска ближайших соседей между двумя наборами данных, неконтролируемые алгоритмы в sklearn.neighbors может быть использован:

>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)
>>> distances
array([[0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356],
       [0.        , 1.        ],
       [0.        , 1.        ],
       [0.        , 1.41421356]])

Поскольку тестовое множество совпадает с обучающим, ближайший сосед каждой точки — это сама точка на расстоянии ноль.

Также можно эффективно создать разреженный граф, показывающий соединения между соседними точками:

>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
       [1., 1., 0., 0., 0., 0.],
       [0., 1., 1., 0., 0., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 1., 1., 0.],
       [0., 0., 0., 0., 1., 1.]])

Набор данных структурирован таким образом, что точки, близкие по порядку индекса, близки в пространстве параметров, что приводит к приблизительно блочно-диагональной матрице K-ближайших соседей. Такая разреженная графовая структура полезна в различных ситуациях, использующих пространственные отношения между точками для обучения без учителя: в частности, см. Isomap, LocallyLinearEmbedding, и SpectralClustering.

1.6.1.2. Классы KDTree и BallTree

В качестве альтернативы можно использовать KDTree или BallTree классы напрямую для поиска ближайших соседей. Это функциональность, обёрнутая NearestNeighbors класс, использованный выше. Ball Tree и KD Tree имеют одинаковый интерфейс; мы покажем пример использования KD Tree здесь:

>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
       [1, 0],
       [2, 1],
       [3, 4],
       [4, 3],
       [5, 4]]...)

См. KDTree и BallTree документация класса для получения дополнительной информации о доступных опциях поиска ближайших соседей, включая спецификацию стратегий запросов, метрик расстояния и т.д. Для списка допустимых метрик используйте KDTree.valid_metrics и BallTree.valid_metrics:

>>> from sklearn.neighbors import KDTree, BallTree
>>> KDTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity']
>>> BallTree.valid_metrics
['euclidean', 'l2', 'minkowski', 'p', 'manhattan', 'cityblock', 'l1', 'chebyshev', 'infinity', 'seuclidean', 'mahalanobis', 'hamming', 'canberra', 'braycurtis', 'jaccard', 'dice', 'rogerstanimoto', 'russellrao', 'sokalmichener', 'sokalsneath', 'haversine', 'pyfunc']

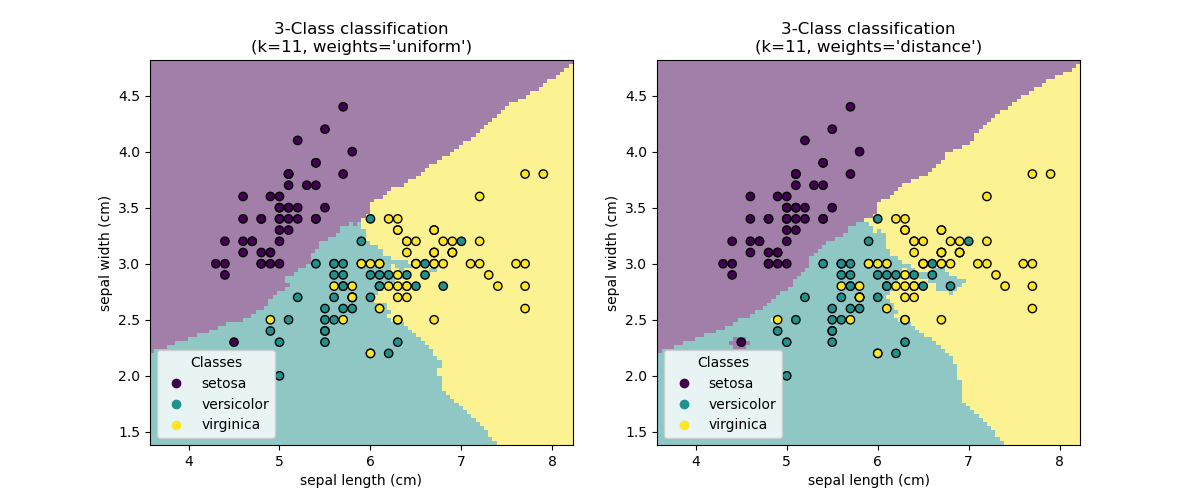
1.6.2. Классификация методом ближайших соседей

Классификация на основе соседей — это тип обучение на основе экземпляров или необобщающее обучение: он не пытается построить общую внутреннюю модель, а просто хранит экземпляры обучающих данных. Классификация вычисляется на основе простого большинства голосов ближайших соседей каждой точки: запрашиваемая точка назначается классу данных, который имеет наибольшее количество представителей среди ближайших соседей точки.

scikit-learn реализует два различных классификатора ближайших соседей: KNeighborsClassifier реализует обучение на основе \(k\) ближайшие соседи каждой точки запроса, где \(k\) является целочисленным значением, указанным пользователем. RadiusNeighborsClassifier реализует обучение на основе количества соседей в пределах фиксированного радиуса \(r\) каждой точки обучения, где \(r\) является значением с плавающей точкой, заданным пользователем.

The \(k\)-ближайших соседей в классификации KNeighborsClassifier является наиболее часто используемой техникой. Оптимальный выбор значения \(k\) сильно зависит от данных: в общем случае большее \(k\) подавляет эффекты шума, но делает границы классификации менее чёткими.

В случаях, когда данные не равномерно распределены, классификация соседей по радиусу в RadiusNeighborsClassifier может быть лучшим выбором. Пользователь указывает фиксированный радиус \(r\), так что точки в более разреженных окрестностях используют меньше ближайших соседей для классификации. Для высокоразмерных пространств параметров этот метод становится менее эффективным из-за так называемого «проклятия размерности».

Базовая классификация ближайших соседей использует равномерные веса: то есть значение, присвоенное точке запроса, вычисляется из простого большинства голосов ближайших соседей. В некоторых обстоятельствах лучше взвесить соседей так, чтобы более близкие соседи вносили больший вклад в подгонку. Это может быть достигнуто через weights ключевое слово. Значение по умолчанию, weights = 'uniform', присваивает равные веса каждому соседу. weights = 'distance' назначает веса, пропорциональные обратному расстоянию от точки запроса. Альтернативно, пользовательская функция расстояния может быть предоставлена для вычисления весов.

Примеры

• Классификация методом ближайших соседей: пример классификации с использованием ближайших соседей.

1.6.3. Регрессия методом ближайших соседей

Регрессия на основе соседей может использоваться в случаях, когда метки данных являются непрерывными, а не дискретными переменными. Метка, назначенная точке запроса, вычисляется на основе среднего значения меток ее ближайших соседей.

scikit-learn реализует два различных регрессора ближайших соседей: KNeighborsRegressor реализует обучение на основе \(k\) ближайшие соседи каждой точки запроса, где \(k\) является целочисленным значением, указанным пользователем. RadiusNeighborsRegressor реализует обучение на основе соседей в пределах фиксированного радиуса \(r\) точки запроса, где \(r\) является значением с плавающей точкой, заданным пользователем.

Базовый метод ближайших соседей для регрессии использует равномерные веса: то есть, каждая точка в локальной окрестности вносит равномерный вклад в классификацию запрашиваемой точки. В некоторых обстоятельствах может быть выгодно взвешивать точки так, чтобы ближайшие точки вносили больший вклад в регрессию, чем удаленные точки. Это может быть достигнуто с помощью weights ключевое слово. Значение по умолчанию, weights = 'uniform'присваивает равные веса всем точкам. weights = 'distance' назначает веса, пропорциональные обратному расстоянию от точки запроса. В качестве альтернативы может быть предоставлена пользовательская функция расстояния, которая будет использоваться для вычисления весов.

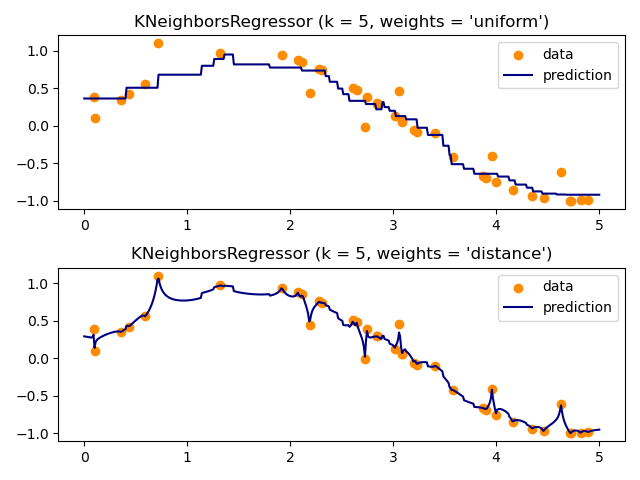
Использование многомерных ближайших соседей для регрессии демонстрируется в Завершение лица с помощью многоканальных оценщиков. В этом примере входы X — пиксели верхней половины лиц, а выходы Y — пиксели нижней половины этих лиц.

Примеры

• Регрессия методом ближайших соседей: пример регрессии с использованием ближайших соседей.

• Завершение лица с помощью многоканальных оценщиков: пример многомерной регрессии с использованием ближайших соседей.

1.6.4. Алгоритмы ближайших соседей

1.6.4.1. Brute Force

Быстрое вычисление ближайших соседей - это активная область исследований в машинном обучении. Самая наивная реализация поиска соседей включает вычисление расстояний между всеми парами точек в наборе данных методом грубой силы: для \(N\) образцы в \(D\) размерностей, этот подход масштабируется как \(O[D N^2]\). Эффективный поиск ближайших соседей полным перебором может быть очень конкурентоспособным для небольших выборок данных. Однако по мере увеличения количества образцов \(N\) растёт, метод полного перебора быстро становится неосуществимым. В классах внутри sklearn.neighbors, поиск соседей методом грубой силы указывается с помощью ключевого слова algorithm = 'brute', и вычисляются с использованием процедур, доступных в sklearn.metrics.pairwise.

1.6.4.2. K-D Tree

Для решения проблемы вычислительной неэффективности полного перебора было изобретено множество древовидных структур данных. В общем случае эти структуры пытаются уменьшить необходимое количество вычислений расстояний, эффективно кодируя агрегированную информацию о расстояниях для выборки. Основная идея заключается в том, что если точка \(A\) очень удалён от точки \(B\), и точка \(B\) очень близко к точке \(C\), тогда мы знаем, что точки \(A\) и \(C\) очень далеки, без необходимости явного вычисления их расстояния. Таким образом, вычислительная стоимость поиска ближайших соседей может быть уменьшена до \(O[D N \log(N)]\) или лучше. Это значительное улучшение по сравнению с полным перебором для больших \(N\).

Ранний подход к использованию этой агрегированной информации был KD-дерево структура данных (сокращение от K-мерное дерево), который обобщает двумерные Квадродеревья и 3-мерные Окт-деревья до произвольного числа измерений. KD-дерево — это бинарная древовидная структура, которая рекурсивно разделяет пространство параметров вдоль осей данных, деля его на вложенные ортотропные области, в которые помещаются точки данных. Построение KD-дерева очень быстрое: поскольку разделение выполняется только вдоль осей данных, не требуется \(D\)-мерные расстояния должны быть вычислены. После построения ближайший сосед точки запроса может быть определён только с помощью \(O[\log(N)]\) вычисления расстояний. Хотя подход KD-дерева очень быстр для низкоразмерных (\(D < 20\)) поиск соседей становится неэффективным, так как \(D\) становится очень большим: это одно из проявлений так называемого "проклятия размерности". В scikit-learn поиск соседей по KD-дереву задается с помощью ключевого слова algorithm = 'kd_tree', и вычисляются с использованием класса KDTree.

Ссылки

• “Многомерные двоичные деревья поиска, используемые для ассоциативного поиска”, Bentley, J.L., Communications of the ACM (1975)

1.6.4.3. Ball Tree

Чтобы устранить неэффективность KD-деревьев в более высоких измерениях, ball tree была разработана структура данных. В то время как KD-деревья разделяют данные вдоль декартовых осей, ball trees разделяют данные в серии вложенных гиперсфер. Это делает построение дерева более затратным, чем для KD-дерева, но приводит к структуре данных, которая может быть очень эффективной для высокоструктурированных данных, даже в очень высоких размерностях.

Дерево шаров рекурсивно делит данные на узлы, определенные центроидом \(C\) и радиус \(r\), так что каждая точка в узле лежит внутри гиперсферы, определенной \(r\) и \(C\). Количество кандидатов для поиска соседей уменьшается за счет использования неравенство треугольника:

\[|x+y| \leq |x| + |y|\]

При такой настройке одного вычисления расстояния между тестовой точкой и центроидом достаточно, чтобы определить нижнюю и верхнюю границы расстояния до всех точек внутри узла. Из-за сферической геометрии узлов ball tree он может превзойти KD-tree в высоких размерностях, хотя фактическая производительность сильно зависит от структуры обучающих данных. В scikit-learn поиск соседей на основе ball-tree задается с помощью ключевого слова algorithm = 'ball_tree', и вычисляются с использованием класса BallTree. Альтернативно, пользователь может работать с BallTree класс напрямую.

Ссылки

• "Пять алгоритмов построения Balltree", Omohundro, S.M., International Computer Science Institute Technical Report (1989)

Выбор алгоритма ближайших соседей

Оптимальный алгоритм для данного набора данных — сложный выбор, который зависит от ряда факторов:

• количество выборок \(N\) (т.е. n_samples) и размерность \(D\) (т.е. n_features).

  • Метод грубой силы время запроса растёт как \(O[D N]\)

  • Ball tree время запроса растёт примерно как \(O[D \log(N)]\)

  • KD-дерево время запроса изменяется с \(D\) таким образом, что это трудно точно охарактеризовать. Для малых \(D\) (менее 20 или около того) стоимость приблизительно \(O[D\log(N)]\), и запрос к KD-дереву может быть очень эффективным. Для больших \(D\), стоимость возрастает почти до \(O[DN]\), и накладные расходы из-за древовидной структуры могут привести к запросам, которые медленнее, чем полный перебор.

  Для небольших наборов данных (\(N\) Определяет генератор псевдослучайных чисел для перемешивания данных. Передайте целое число для воспроизводимых результатов при множественных вызовах функции. См. \(\log(N)\) сопоставим с \(N\), и алгоритмы полного перебора могут быть эффективнее чем подход на основе дерева. Оба KDTree и BallTree решает эту проблему, предоставляя размер листа параметр: это контролирует количество выборок, при котором запрос переключается на полный перебор. Это позволяет обоим алгоритмам приближаться к эффективности полного перебора для малых \(N\).

• структура данных: внутренняя размерность данных и/или разреженность данных. Внутренняя размерность относится к размерности \(d \le D\) многообразия, на котором лежат данные, которое может быть линейно или нелинейно вложено в пространство параметров. Разреженность относится к степени, в которой данные заполняют пространство параметров (это следует отличать от концепции, используемой в "разреженных" матрицах. Матрица данных может не иметь нулевых записей, но структура может всё ещё быть "разреженным" в этом смысле).

  • Метод грубой силы время запроса не изменяется структурой данных.

  • Ball tree и KD-дерево время запросов может сильно зависеть от структуры данных. В целом, более разреженные данные с меньшей внутренней размерностью приводят к более быстрому времени запросов. Поскольку внутреннее представление KD-дерева выровнено по осям параметров, оно обычно не показывает такого же улучшения, как ball tree для произвольно структурированных данных.

  Наборы данных, используемые в машинном обучении, как правило, очень структурированы и очень хорошо подходят для запросов на основе деревьев.

• количество соседей \(k\) запрошено для точки запроса.

  • Метод грубой силы время запроса в значительной степени не зависит от значения \(k\)

  • Ball tree и KD-дерево время запроса будет замедляться по мере \(k\) увеличивается. Это связано с двумя эффектами: во-первых, больший \(k\) приводит к необходимости поиска большей части пространства параметров. Во-вторых, использование \(k > 1\) требует внутренней очереди результатов при обходе дерева.

  Поскольку \(k\) становится большим по сравнению с \(N\), способность обрезать ветви в запросе на основе дерева снижается. В этой ситуации запросы методом грубой силы могут быть более эффективными.

• количество запрашиваемых точек. И ball tree, и KD Tree требуют фазы построения. Стоимость этого построения становится незначительной при усреднении по многим запросам. Однако если будет выполнено только небольшое количество запросов, построение может составлять значительную часть общей стоимости. Если требуется очень мало запрашиваемых точек, метод грубой силы лучше, чем метод на основе дерева.

В настоящее время, algorithm = 'auto' выбирает 'brute' если выполняется любое из следующих условий:

• входные данные разрежены

• metric = 'precomputed'

• \(D > 15\)

• \(k >= N/2\)

• effective_metric_ не находится в VALID_METRICS список для любого из 'kd_tree' или 'ball_tree'

В противном случае выбирается первый из 'kd_tree' и 'ball_tree' который имеет effective_metric_ в его VALID_METRICS список. Эта эвристика основана на следующих предположениях:

• количество точек запроса по крайней мере того же порядка, что и количество точек обучения

• leaf_size близко к значению по умолчанию 30

• когда \(D > 15\), внутренняя размерность данных обычно слишком высока для методов на основе деревьев

Эффект leaf_size

Как отмечено выше, для небольших размеров выборки поиск методом грубой силы может быть более эффективным, чем запрос на основе дерева. Этот факт учитывается в ball tree и KD tree путем внутреннего переключения на поиск методом грубой силы внутри листовых узлов. Уровень этого переключения может быть указан с помощью параметра leaf_size. Этот выбор параметра имеет множество эффектов:

время построения

Большее leaf_size приводит к более быстрому времени построения дерева, потому что нужно создавать меньше узлов

время запроса

Как большое, так и маленькое leaf_size может привести к субоптимальной стоимости запроса. Для leaf_size При приближении к 1, накладные расходы на обход узлов могут значительно замедлить время выполнения запросов. leaf_size приближаясь к размеру обучающей выборки, запросы становятся по сути полным перебором. Хороший компромисс между ними — leaf_size = 30, значение по умолчанию параметра.

память

Поскольку leaf_size увеличивается, память, необходимая для хранения древовидной структуры, уменьшается. Это особенно важно в случае ball tree, который хранит \(D\)-мерный центроид для каждого узла. Необходимое пространство хранения для BallTree приблизительно 1 / leaf_size раз размер обучающей выборки.

leaf_size не используется для запросов методом грубой силы.

Допустимые метрики для алгоритмов ближайших соседей

Список доступных метрик см. в документации DistanceMetric класс и метрики, перечисленные в sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS. Обратите внимание, что метрика "cosine" использует cosine_distances.

Список допустимых метрик для любого из вышеуказанных алгоритмов можно получить, используя их valid_metric атрибут. Например, допустимые метрики для KDTree может быть сгенерировано:

>>> from sklearn.neighbors import KDTree
>>> print(sorted(KDTree.valid_metrics))
['chebyshev', 'cityblock', 'euclidean', 'infinity', 'l1', 'l2', 'manhattan', 'minkowski', 'p']

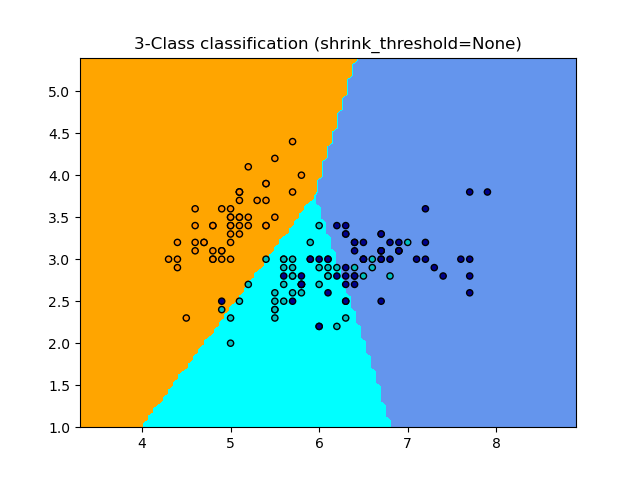
1.6.5. Классификатор ближайшего центроида

The NearestCentroid классификатор — это простой алгоритм, который представляет каждый класс центроидом его элементов. По сути, это делает его похожим на фазу обновления меток в KMeans алгоритм. Он также не имеет параметров для выбора, что делает его хорошим базовым классификатором. Однако он страдает на невыпуклых классах, а также когда классы имеют сильно различающиеся дисперсии, поскольку предполагается равная дисперсия во всех измерениях. См. Линейный дискриминантный анализ (LinearDiscriminantAnalysis) и квадратичный дискриминантный анализ (QuadraticDiscriminantAnalysis) для более сложных методов, которые не делают это предположение. Использование значения по умолчанию NearestCentroid просто:

>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]

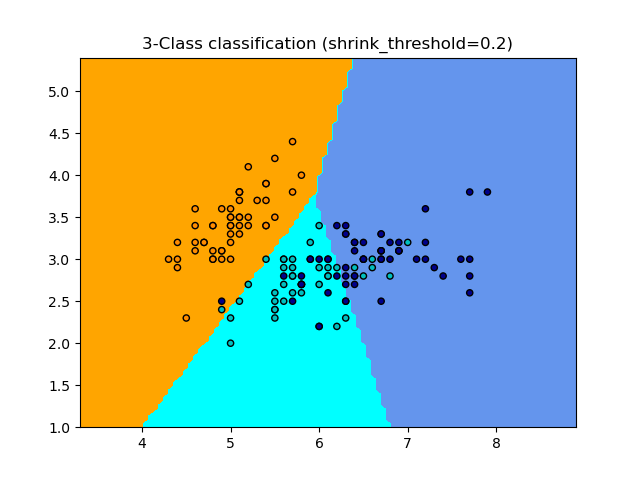
1.6.5.1. Ближайший сжатый центроид

The NearestCentroid классификатор имеет shrink_threshold параметр, который реализует классификатор ближайшего сжатого центроида. По сути, значение каждого признака для каждого центроида делится на внутриклассовую дисперсию этого признака. Затем значения признаков уменьшаются на shrink_thresholdНаиболее заметно, что если конкретное значение признака пересекает ноль, оно устанавливается в ноль. По сути, это удаляет признак из влияния на классификацию. Это полезно, например, для удаления шумных признаков.

В примере ниже использование небольшого порога сжатия увеличивает точность модели с 0.81 до 0.82.

Примеры

• Классификация по ближайшему центроиду: пример классификации с использованием ближайшего центроида с разными порогами сжатия.

1.6.6. Трансформер ближайших соседей

Многие оценщики scikit-learn полагаются на ближайших соседей: несколько классификаторов и регрессоров, таких как KNeighborsClassifier и KNeighborsRegressor, но также некоторые методы кластеризации, такие как DBSCAN и SpectralClustering, и некоторые вложения многообразий, такие как TSNE и Isomap.

Все эти оценщики могут вычислять ближайших соседей внутренне, но большинство из них также принимают предварительно вычисленных ближайших соседей разреженный граф, как дано kneighbors_graph и radius_neighbors_graph. С режимом mode='connectivity', эти функции возвращают разреженный граф смежности в двоичном формате, как требуется, например, в SpectralClustering. В то время как с mode='distance', они возвращают разреженный граф расстояний, как требуется, например, в DBSCAN. Чтобы включить эти функции в конвейер scikit-learn, можно также использовать соответствующие классы KNeighborsTransformer и RadiusNeighborsTransformer. Преимущества этого API разреженного графа многочисленны.

Во-первых, предвычисленный граф может использоваться многократно, например, при изменении параметра оценщика. Это можно сделать вручную пользователем или с использованием свойств кэширования конвейера scikit-learn:

>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir()  # we use a temporary folder here
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
...     KNeighborsTransformer(mode='distance'),
...     Isomap(n_components=3, metric='precomputed'),
...     memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)

Во-вторых, предварительное вычисление графа может дать более тонкий контроль над оценкой ближайших соседей, например, позволяя использовать многопроцессорность через параметр n_jobs, который может быть недоступен во всех оценщиках.

Наконец, предварительные вычисления могут быть выполнены пользовательскими оценщиками для использования различных реализаций, таких как методы приближенных ближайших соседей или реализации с особыми типами данных. Предварительно вычисленные соседи разреженный граф должен быть отформатирован как в radius_neighbors_graph вывод:

• матрица CSR (хотя COO, CSC или LIL также принимаются).

• явно хранит только ближайшие окрестности каждого образца относительно обучающих данных. Это должно включать те, что находятся на нулевом расстоянии от точки запроса, включая диагональ матрицы при вычислении ближайших окрестностей между обучающими данными и самими собой.

• каждой строки data должны хранить расстояние в порядке возрастания (опционально. Несортированные данные будут стабильно отсортированы, добавляя вычислительные накладные расходы).

• все значения в данных должны быть неотрицательными.

• не должно быть дубликатов indices в любой строке (см. scipy/scipy#5807).

• если алгоритму, которому передаётся предвычисленная матрица, требуется k ближайших соседей (в отличие от окрестности по радиусу), в каждой строке должно храниться не менее k соседей (или k+1, как объяснено в следующем примечании).

Примечание

Когда запрашивается определенное количество соседей (с использованием KNeighborsTransformer), определение n_neighbors неоднозначен, поскольку он может либо включать каждую обучающую точку как своего собственного соседа, либо исключать их. Ни один из вариантов не идеален, поскольку включение приводит к разному количеству несоседних точек во время обучения и тестирования, а исключение приводит к различию между fit(X).transform(X) и fit_transform(X), что противоречит API scikit-learn. В KNeighborsTransformer мы используем определение, которое включает каждую обучающую точку как своего собственного соседа в подсчёте n_neighbors. Однако, по причинам совместимости с другими оценщиками, которые используют другое определение, один дополнительный сосед будет вычислен, когда mode == 'distance'. Для максимальной совместимости со всеми оценщиками безопасным выбором является всегда включать одного дополнительного соседа в пользовательском оценщике ближайших соседей, поскольку ненужные соседи будут отфильтрованы последующими оценщиками.

Примеры

• Приближенные ближайшие соседи в TSNE: пример конвейеризации KNeighborsTransformer и TSNE. Также предлагает два пользовательских оценщика ближайших соседей, основанных на внешних пакетах.

• Кэширование ближайших соседей: пример конвейеризации KNeighborsTransformer и KNeighborsClassifier для включения кэширования графа соседей во время поиска по сетке гиперпараметров.

1.6.7. Анализ компонентов соседства

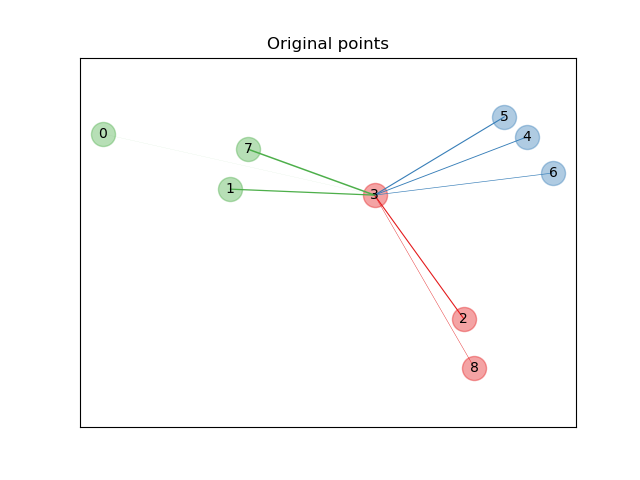
Анализ компонентов соседства (NCA, NeighborhoodComponentsAnalysis) — это алгоритм обучения метрики расстояния, который направлен на повышение точности классификации ближайших соседей по сравнению со стандартным евклидовым расстоянием. Алгоритм напрямую максимизирует стохастический вариант оценки leave-one-out k-ближайших соседей (KNN) на обучающем наборе. Он также может изучать низкоразмерную линейную проекцию данных, которую можно использовать для визуализации данных и быстрой классификации.

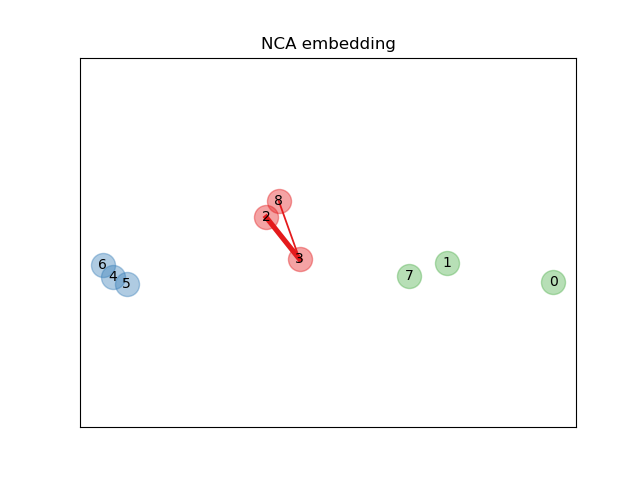
На приведенном выше иллюстративном рисунке мы рассматриваем некоторые точки из случайно сгенерированного набора данных. Мы фокусируемся на стохастической классификации KNN точки № 3. Толщина связи между образцом 3 и другой точкой пропорциональна их расстоянию и может рассматриваться как относительный вес (или вероятность), который стохастическое правило предсказания ближайших соседей присвоило бы этой точке. В исходном пространстве у образца 3 много стохастических соседей из различных классов, поэтому правильный класс не очень вероятен. Однако в проецируемом пространстве, изученном NCA, единственные стохастические соседи с незначительным весом принадлежат тому же классу, что и образец 3, гарантируя, что последний будет хорошо классифицирован. См. математическая формулировка для получения дополнительной информации.

1.6.7.1. Классификация

В сочетании с классификатором ближайших соседей (KNeighborsClassifier), NCA привлекателен для классификации, поскольку он естественным образом обрабатывает многоклассовые задачи без увеличения размера модели и не вводит дополнительные параметры, требующие тонкой настройки пользователем.

Классификация NCA показала хорошие результаты на практике для наборов данных различного размера и сложности. В отличие от связанных методов, таких как линейный дискриминантный анализ, NCA не делает никаких предположений о распределениях классов. Классификация ближайшего соседа может естественным образом создавать сильно нерегулярные границы решений.

Чтобы использовать эту модель для классификации, необходимо объединить NeighborhoodComponentsAnalysis экземпляр, который изучает оптимальное преобразование с KNeighborsClassifier экземпляр, который выполняет классификацию в проецируемом пространстве. Вот пример с двумя классами:

>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...

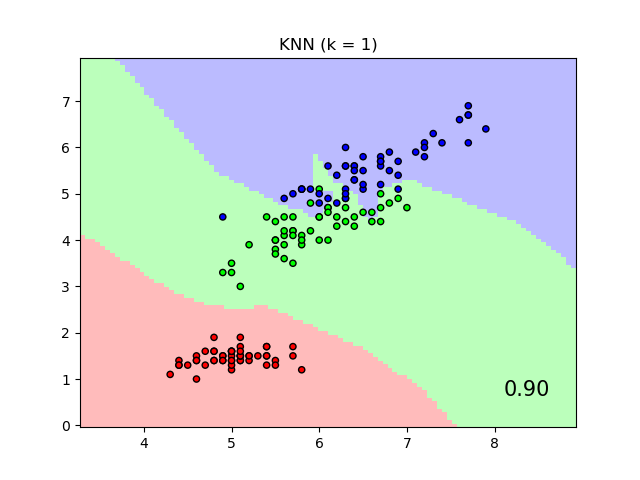
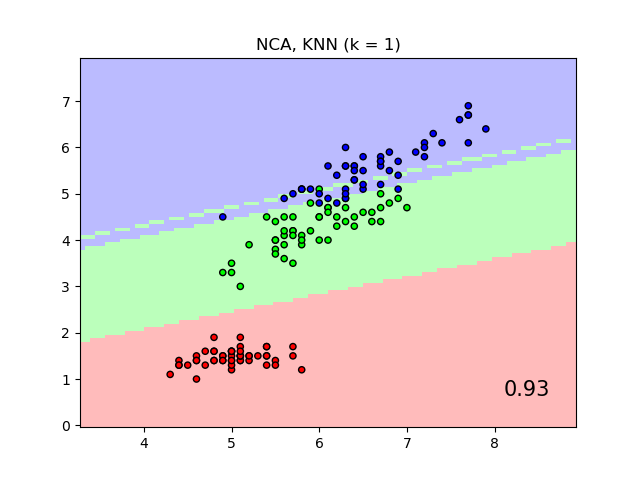
График показывает границы решений для классификации ближайших соседей и классификации Neighborhood Components Analysis на наборе данных iris, когда обучение и оценка выполняются только по двум признакам для целей визуализации.

1.6.7.2. Снижение размерности

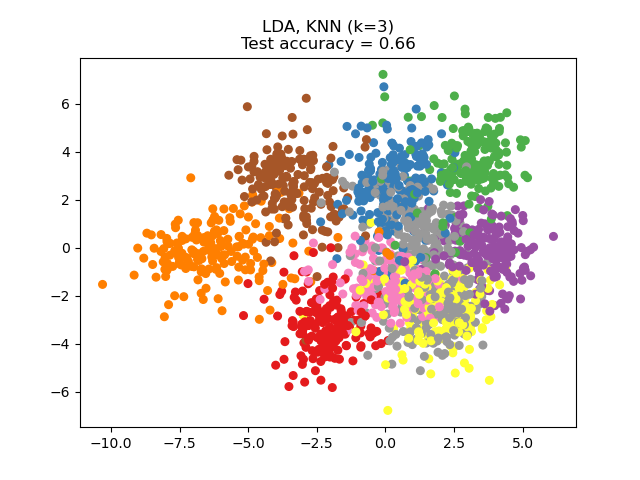
NCA может использоваться для контролируемого понижения размерности. Входные данные проецируются на линейное подпространство, состоящее из направлений, которые минимизируют целевую функцию NCA. Желаемую размерность можно задать с помощью параметра n_components. Например, следующий рисунок показывает сравнение снижения размерности с методом главных компонент (PCA), Линейный дискриминантный анализ (LinearDiscriminantAnalysis) и Анализ компонентов соседства (NeighborhoodComponentsAnalysis) на наборе данных Digits, наборе данных размером \(n_{samples} = 1797\) и \(n_{features} = 64\). Набор данных разделяется на обучающую и тестовую выборки равного размера, затем стандартизируется. Для оценки вычисляется точность классификации по 3 ближайшим соседям на 2-мерных спроецированных точках, найденных каждым методом. Каждый образец данных принадлежит одному из 10 классов.

Примеры

• Сравнение ближайших соседей с анализом компонент соседства и без него

• Снижение размерности с помощью анализа компонентов соседства

• Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap…

1.6.7.3. Математическая формулировка

Цель NCA — изучить оптимальную матрицу линейного преобразования размера (n_components, n_features), который максимизирует сумму по всем выборкам \(i\) вероятности \(p_i\) что \(i\) правильно классифицирован, т.е.:

\[\underset{L}{\arg\max} \sum\limits_{i=0}^{N - 1} p_{i}\]

с \(N\) = n_samples и \(p_i\) вероятность образца \(i\) правильно классифицируются согласно стохастическому правилу ближайших соседей в изученном вложенном пространстве:

\[p_{i}=\sum\limits_{j \in C_i}{p_{i j}}\]

где \(C_i\) является множеством точек того же класса, что и выборка \(i\), и \(p_{i j}\) это softmax по евклидовым расстояниям во вложенном пространстве:

\[p_{i j} = \frac{\exp(-||L x_i - L x_j||^2)}{\sum\limits_{k \ne i} {\exp{-(||L x_i - L x_k||^2)}}} , \quad p_{i i} = 0\]

Расстояние Махаланобиса

NCA можно рассматривать как обучение (квадратичной) метрике расстояния Махаланобиса:

\[|| L(x_i - x_j)||^2 = (x_i - x_j)^TM(x_i - x_j),\]

где \(M = L^T L\) является симметричной положительно полуопределённой матрицей размера (n_features, n_features).

1.6.7.4. Реализация

Эта реализация следует тому, что объяснено в оригинальной статье [1]. Для метода оптимизации в настоящее время используется L-BFGS-B из scipy с полным вычислением градиента на каждой итерации, чтобы избежать настройки скорости обучения и обеспечить стабильное обучение.

См. примеры ниже и строку документации NeighborhoodComponentsAnalysis.fit для получения дополнительной информации.

1.6.7.5. Сложность

1.6.7.5.1. Обучение

NCA хранит матрицу попарных расстояний, занимая n_samples ** 2 память. Временная сложность зависит от количества итераций, выполненных алгоритмом оптимизации. Однако можно установить максимальное количество итераций с помощью аргумента max_iter. Для каждой итерации временная сложность составляет O(n_components x n_samples x min(n_samples, n_features)).

1.6.7.5.2. Преобразование

Здесь transform операция возвращает \(LX^T\), поэтому его временная сложность равна n_components * n_features * n_samples_test. В операции не добавляется дополнительная сложность по памяти.

Ссылки

[1]

«Анализ компонентов соседства», J. Goldberger, S. Roweis, G. Hinton, R. Salakhutdinov, Advances in Neural Information Processing Systems, Vol. 17, May 2005, pp. 513-520.

• Запись в Википедии о Neighborhood Components Analysis