1.1. Линейные модели

Следующие методы предназначены для регрессии, в которой целевое значение ожидается как линейная комбинация признаков. В математической нотации, если \(\hat{y}\) является предсказанным значением.

\[\hat{y}(w, x) = w_0 + w_1 x_1 + ... + w_p x_p\]

Во всем модуле мы обозначаем вектор \(w = (w_1, ..., w_p)\) как coef_ и \(w_0\) как intercept_.

Для выполнения классификации с обобщенными линейными моделями см. Логистическая регрессия.

1.1.1. Метод наименьших квадратов

LinearRegression обучает линейную модель с коэффициентами \(w = (w_1, ..., w_p)\) чтобы минимизировать остаточную сумму квадратов между наблюдаемыми целями в наборе данных и целями, предсказанными линейной аппроксимацией. Математически он решает задачу вида:

\[\min_{w} || X w - y||_2^2\]

LinearRegression принимает в своих fit аргументы метода X, y, sample_weight и сохраняет коэффициенты \(w\) линейной модели в ее coef_ и intercept_ атрибуты:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])
>>> reg.intercept_
0.0

Оценки коэффициентов для метода наименьших квадратов зависят от независимости признаков. Когда признаки коррелированы и некоторые столбцы матрицы плана \(X\) имеют приблизительно линейную зависимость, матрица плана становится близкой к вырожденной, и в результате оценка методом наименьших квадратов становится высокочувствительной к случайным ошибкам в наблюдаемой целевой переменной, что приводит к большой дисперсии. Эта ситуация мультиколлинеарность может возникнуть, например, когда данные собираются без экспериментального дизайна.

Примеры

• Метод наименьших квадратов и гребневая регрессия

1.1.1.1. Неотрицательные наименьшие квадраты

Можно ограничить все коэффициенты, чтобы они были неотрицательными, что может быть полезно, когда они представляют некоторые физические или естественно неотрицательные величины (например, частотные подсчеты или цены товаров). LinearRegression принимает булево значение positive параметр: при установке в True Неотрицательные наименьшие квадраты затем применяются.

Примеры

• Метод наименьших квадратов с неотрицательными ограничениями

1.1.1.2. Сложность метода наименьших квадратов

Решение методом наименьших квадратов вычисляется с использованием сингулярного разложения \(X\). Если \(X\) является матрицей формы (n_samples, n_features) этот метод имеет стоимость \(O(n_{\text{samples}} n_{\text{features}}^2)\), предполагая, что \(n_{\text{samples}} \geq n_{\text{features}}\).

1.1.2. Ридж-регрессия и классификация

1.1.2.1. Регрессия

Ridge . То есть, мы будем считать две модели практически эквивалентными, если они отличаются менее чем на 1% по своей производительности. Метод наименьших квадратов путём наложения штрафа на размер коэффициентов. Коэффициенты гребня минимизируют штрафную сумму квадратов остатков:

\[\min_{w} || X w - y||_2^2 + \alpha ||w||_2^2\]

Параметр сложности \(\alpha \geq 0\) управляет степенью сжатия: чем больше значение \(\alpha\), тем больше степень сжатия и, следовательно, коэффициенты становятся более устойчивыми к коллинеарности.

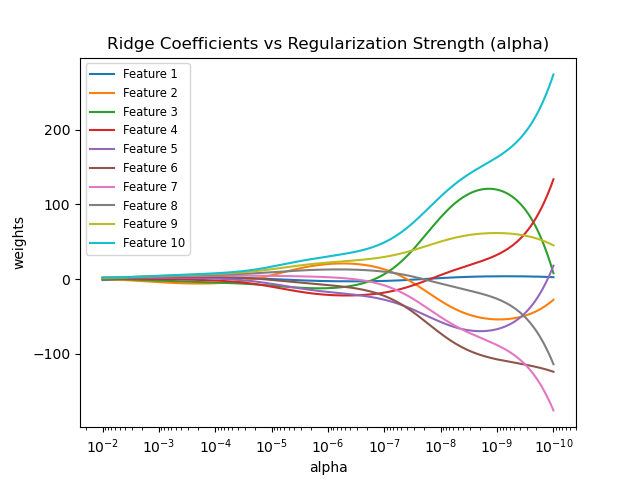
Как и в других линейных моделях, Ridge будет принимать в своем fit метод массивы X, y и будет хранить коэффициенты \(w\) линейной модели в её coef_ член:

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
np.float64(0.13636)

Обратите внимание, что класс Ridge позволяет пользователю указать, что решатель будет автоматически выбран путем установки solver="auto". Когда эта опция указана, Ridge будет выбирать между "lbfgs", "cholesky", и "sparse_cg" солверы. Ridge начнет проверять условия, показанные в следующей таблице, сверху вниз. Если условие истинно, выбирается соответствующий решатель.

Решатель	Условие
'lbfgs'	The positive=True опция указана.
‘cholesky’	Входной массив X не является разреженным.
‘sparse_cg’	Ни одно из вышеуказанных условий не выполнено.

Примеры

• Метод наименьших квадратов и гребневая регрессия

• Построение коэффициентов Ridge как функции регуляризации

• Распространённые ошибки в интерпретации коэффициентов линейных моделей

• Коэффициенты Ridge как функция L2-регуляризации

1.1.2.2. Классификация

The Ridge регрессор имеет вариант классификатора: RidgeClassifier. Этот классификатор сначала преобразует бинарные цели в {-1, 1} и затем рассматривает задачу как регрессионную, оптимизируя ту же целевую функцию, что и выше. Предсказанный класс соответствует знаку предсказания регрессора. Для многоклассовой классификации задача рассматривается как многомерная регрессия, и предсказанный класс соответствует выходу с наибольшим значением.

Может показаться сомнительным использовать (регуляризованную) функцию потерь наименьших квадратов для обучения классификационной модели вместо более традиционных логистических или hinge функций потерь. Однако на практике все эти модели могут приводить к схожим кросс-валидационным оценкам с точки зрения точности или precision/recall, в то время как регуляризованная функция потерь наименьших квадратов, используемая RidgeClassifier позволяет очень разный выбор численных решателей с различными профилями вычислительной производительности.

The RidgeClassifier может быть значительно быстрее, чем, например, LogisticRegression с большим количеством классов, так как может вычислять матрицу проекции \((X^T X)^{-1} X^T\) только один раз.

Этот классификатор иногда называют Машина опорных векторов методом наименьших квадратов с линейным ядром.

Примеры

• Классификация текстовых документов с использованием разреженных признаков

1.1.2.3. Сложность Ridge

Этот метод имеет тот же порядок сложности, что и Метод наименьших квадратов.

1.1.2.4. Установка параметра регуляризации: перекрестная проверка с исключением по одному

RidgeCV и RidgeClassifierCV реализуют ridge регрессию/классификацию со встроенной кросс-валидацией параметра alpha. Они работают так же, как GridSearchCV за исключением того, что по умолчанию используется эффективный метод Leave-One-Out кросс-валидация. При использовании значения по умолчанию кросс-валидация, alpha не может быть 0 из-за формулы, используемой для вычисления ошибки Leave-One-Out. См. [RL2007] подробности.

Пример использования:

>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
      1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
np.float64(0.01)

Указание значения cv атрибут вызовет использование кросс-валидации с GridSearchCV, например cv=10 для 10-кратной кросс-валидации, а не для Leave-One-Out Cross-Validation.

Ссылки

[RL2007]

“Заметки о регуляризованном методе наименьших квадратов”, Рифкин и Липперт (технический отчет, слайды курса).

1.1.3. Lasso

The Lasso является линейной моделью, которая оценивает разреженные коэффициенты, т.е., она способна устанавливать коэффициенты точно в ноль. Это полезно в некоторых контекстах из-за её тенденции предпочитать решения с меньшим количеством ненулевых коэффициентов, эффективно уменьшая количество признаков, от которых зависит данное решение. По этой причине Lasso и его варианты являются фундаментальными для области сжатого зондирования. При определённых условиях он может восстановить точный набор ненулевых коэффициентов (см. Компрессионное зондирование: реконструкция томографии с априорным распределением L1 (Lasso)).

Математически это линейная модель с добавленным регуляризационным членом. Целевая функция для минимизации:

\[\min_{w} P(w) = {\frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha ||w||_1}\]

Оценка лассо, таким образом, решает задачу наименьших квадратов с добавленным штрафом \(\alpha ||w||_1\), где \(\alpha\) является константой и \(||w||_1\) является \(\ell_1\)-норма вектора коэффициентов.

Реализация в классе Lasso использует координатный спуск в качестве алгоритма для подбора коэффициентов. См. Least Angle Regression для другой реализации:

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])

Функция lasso_path полезен для задач более низкого уровня, так как вычисляет коэффициенты вдоль всего пути возможных значений.

Примеры

• Модели на основе L1 для разреженных сигналов

• Компрессионное зондирование: реконструкция томографии с априорным распределением L1 (Lasso)

• Распространённые ошибки в интерпретации коэффициентов линейных моделей

• Выбор модели Lasso: AIC-BIC / перекрёстная проверка

Примечание

Выбор признаков с помощью Lasso

Поскольку регрессия Лассо дает разреженные модели, она может использоваться для выполнения отбора признаков, как подробно описано в Отбор признаков на основе L1.

Ссылки

Следующие ссылки объясняют происхождение Lasso, а также свойства задачи Lasso и вычисление двойственного разрыва, используемого для контроля сходимости.

• Robert Tibshirani. (1996) Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol., 58(1):267-288

• “Метод внутренней точки для крупномасштабных L1-регуляризованных наименьших квадратов,” С. Дж. Ким, К. Ко, М. Лустиг, С. Бойд и Д. Гориневский, в IEEE Journal of Selected Topics in Signal Processing, 2007 (Статья)

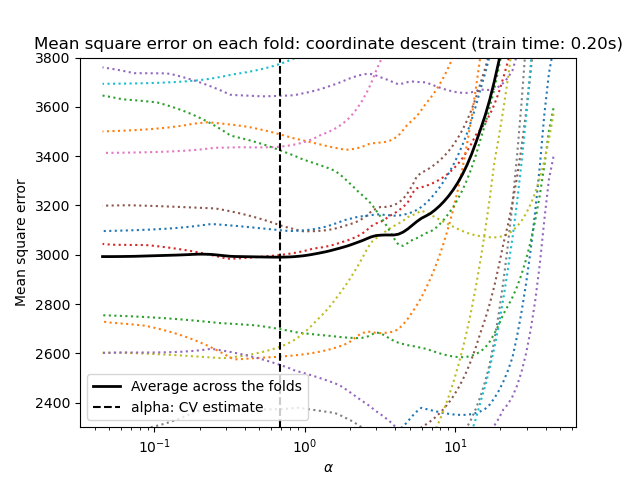
1.1.3.1. Координатный спуск с правилами безопасного отсечения по зазору

Координатный спуск (CD) — это стратегия решения задачи минимизации, которая рассматривает один признак \(j\) за раз. Таким образом, задача оптимизации сводится к одномерной задаче, которую легче решить:

\[\min_{w_j} {\frac{1}{2n_{\text{samples}}} ||x_j w_j + X_{-j}w_{-j} - y||_2 ^ 2 + \alpha |w_j|}\]

с индексом \(-j\) означает все признаки, кроме \(j\). Решение состоит в

\[w_j = \frac{S(x_j^T (y - X_{-j}w_{-j}), \alpha)}{||x_j||_2^2}\]

с функцией мягкого порога \(S(z, \alpha) = \operatorname{sign}(z) \max(0, |z|-\alpha)\). Обратите внимание, что функция мягкого порога точно равна нулю всякий раз, когда \(\alpha \geq |z|\). Затем решатель CD циклически перебирает признаки, выбирая один за другим в порядке, заданном X (selection="cyclic"), или путем случайного выбора признаков (selection="random"). Останавливается, если двойственный зазор меньше заданного допуска tol.

Математические детали

Двойственный разрыв \(G(w, v)\) является верхней границей разницы между текущей целевой функцией Лассо в прямой форме, \(P(w)\), и его минимум \(P(w^\star)\), т.е. \(G(w, v) \geq P(w) - P(w^\star)\). Это задается \(G(w, v) = P(w) - D(v)\) с двойной целевой функцией

\[D(v) = \frac{1}{2n_{\text{samples}}}(y^Tv - ||v||_2^2)\]

при условии \(v \in ||X^Tv||_{\infty} \leq n_{\text{samples}}\alpha\). В оптимальном случае дуальный разрыв равен нулю, \(G(w^\star, v^\star) = 0\) (свойство, называемое сильной двойственностью). С (масштабированной) двойственной переменной \(v = c r\), текущий остаток \(r = y - Xw\) и двойное масштабирование

\[\begin{split}c = \begin{cases} 1, & ||X^Tr||_{\infty} \leq n_{\text{samples}}\alpha, \\ \frac{n_{\text{samples}}\alpha}{||X^Tr||_{\infty}}, & \text{otherwise} \end{cases}\end{split}\]

критерий остановки

\[\text{tol} \frac{||y||_2^2}{n_{\text{samples}}} < G(w, cr)\,.\]

Умный метод для ускорения алгоритма координатного спуска заключается в отсеивании признаков таким образом, чтобы в оптимуме \(w_j = 0\). Правила безопасного отсечения (gap safe screening rules) — это такой инструмент. В любой момент алгоритма оптимизации они могут сказать, какой признак можно безопасно исключить, т.е. установить в ноль с уверенностью.

Ссылки

Первая ссылка объясняет решатель координатного спуска, используемый в scikit-learn, остальные рассматривают правила безопасного отсечения по зазору.

• Friedman, Hastie & Tibshirani. (2010). Regularization Path For Generalized linear Models by Coordinate Descent. J Stat Softw 33(1), 1-22

• О. Ферко, А. Грамфор, Дж. Салмон. (2015). Учитывайте дуальный разрыв: более безопасные правила для Lasso. Proceedings of Machine Learning Research 37:333-342, 2015.

• E. Ndiaye, O. Fercoq, A. Gramfort, J. Salmon. (2017). Gap Safe Screening Rules for Sparsity Enforcing Penalties. Journal of Machine Learning Research 18(128):1-33, 2017.

1.1.3.2. Установка параметра регуляризации

The alpha параметр управляет степенью разреженности оцененных коэффициентов.

1.1.3.2.1. Используя перекрестную проверку

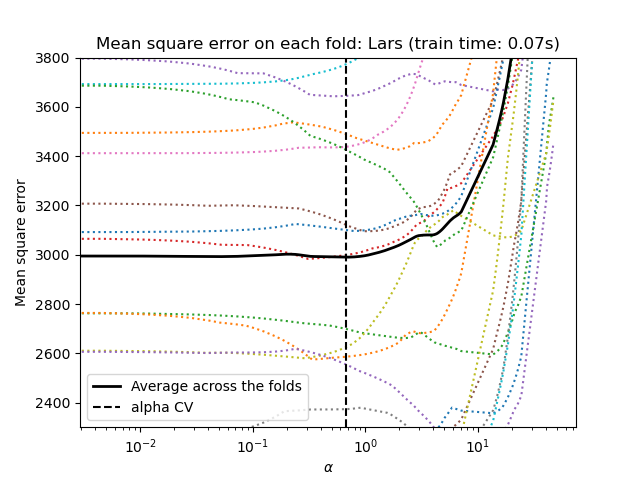
scikit-learn предоставляет объекты, которые устанавливают Lasso alpha параметр с помощью перекрестной проверки: LassoCV и LassoLarsCV. LassoLarsCV основан на Least Angle Regression алгоритм, объясненный ниже.

Для высокоразмерных наборов данных с множеством коллинеарных признаков, LassoCV чаще всего предпочтительнее. Однако, LassoLarsCV имеет преимущество в исследовании более релевантных значений alpha параметр, и если количество образцов очень мало по сравнению с количеством признаков, он часто быстрее, чем LassoCV.

1.1.3.2.2. Выбор модели на основе информационных критериев

В качестве альтернативы, оценщик LassoLarsIC предлагает использовать информационный критерий Акаике (AIC) и байесовский информационный критерий (BIC). Это более дешевая в вычислительном отношении альтернатива для нахождения оптимального значения alpha, так как путь регуляризации вычисляется только один раз вместо k+1 раз при использовании k-кратной перекрестной проверки.

Действительно, эти критерии вычисляются на обучающем наборе данных. Короче говоря, они штрафуют излишне оптимистичные оценки различных моделей Lasso за их гибкость (см. раздел «Математические детали» ниже).

Однако такие критерии требуют правильной оценки степеней свободы решения, выводятся для больших выборок (асимптотические результаты) и предполагают, что исследуемая модель верна. Они также могут давать сбои, когда задача плохо обусловлена (например, признаков больше, чем образцов).

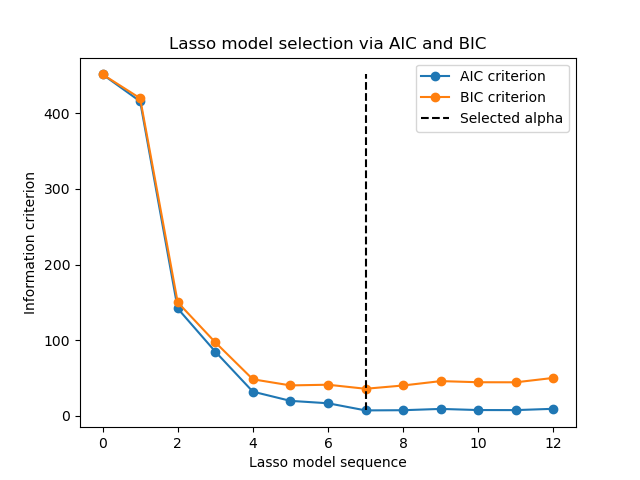
Примеры

• Выбор модели Lasso: AIC-BIC / перекрёстная проверка

• Выбор модели Lasso с помощью информационных критериев

1.1.3.2.3. Критерии AIC и BIC

Определение AIC (и, следовательно, BIC) может различаться в литературе. В этом разделе мы предоставляем дополнительную информацию о критерии, вычисляемом в scikit-learn.

Математические детали

Критерий AIC определяется как:

\[AIC = -2 \log(\hat{L}) + 2 d\]

где \(\hat{L}\) является максимальным правдоподобием модели и \(d\) это количество параметров (также называемых степенями свободы в предыдущем разделе).

Определение BIC заменяет константу \(2\) by \(\log(N)\):

\[BIC = -2 \log(\hat{L}) + \log(N) d\]

где \(N\) это количество образцов.

Для линейной гауссовской модели максимальное правдоподобие определяется как:

\[\log(\hat{L}) = - \frac{n}{2} \log(2 \pi) - \frac{n}{2} \log(\sigma^2) - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{2\sigma^2}\]

где \(\sigma^2\) является оценкой дисперсии шума, \(y_i\) и \(\hat{y}_i\) соответственно истинные и предсказанные цели, и \(n\) это количество образцов.

Подстановка максимального правдоподобия в формулу AIC даёт:

\[AIC = n \log(2 \pi \sigma^2) + \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sigma^2} + 2 d\]

Первый член приведенного выше выражения иногда отбрасывается, поскольку он является константой, когда \(\sigma^2\) предоставляется. Кроме того, иногда утверждается, что AIC эквивалентен \(C_p\) статистика [12]. В строгом смысле, однако, это эквивалентно только с точностью до некоторой константы и мультипликативного коэффициента.

Наконец, мы упомянули выше, что \(\sigma^2\) является оценкой дисперсии шума. В LassoLarsIC когда параметр noise_variance не предоставлен (по умолчанию), дисперсия шума оценивается с помощью несмещенного оценщика [13] определяется как:

\[\sigma^2 = \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n - p}\]

где \(p\) — это количество признаков, а \(\hat{y}_i\) предсказанная целевая переменная с использованием обычной регрессии методом наименьших квадратов. Обратите внимание, что эта формула действительна только когда n_samples > n_features.

Ссылки

[12]

Zou, Hui, Trevor Hastie, and Robert Tibshirani. "On the degrees of freedom of the lasso." The Annals of Statistics 35.5 (2007): 2173-2192.

[13]

Черкасский, Владимир, и Юньцянь Ма. «Сравнение выбора модели для регрессии». Нейронные вычисления 15.7 (2003): 1691-1714.

1.1.3.2.4. Сравнение с параметром регуляризации SVM

Эквивалентность между alpha и параметром регуляризации SVM, C задается формулой alpha = 1 / C или alpha = 1 / (n_samples * C), в зависимости от оценщика и точной целевой функции, оптимизируемой моделью.

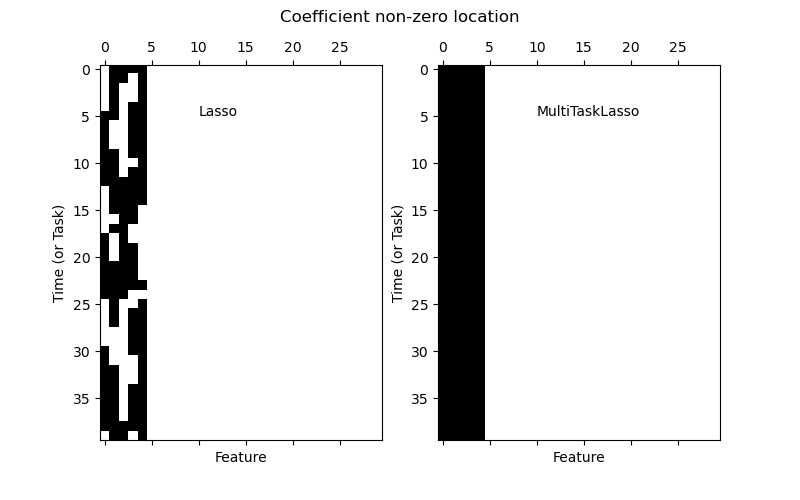
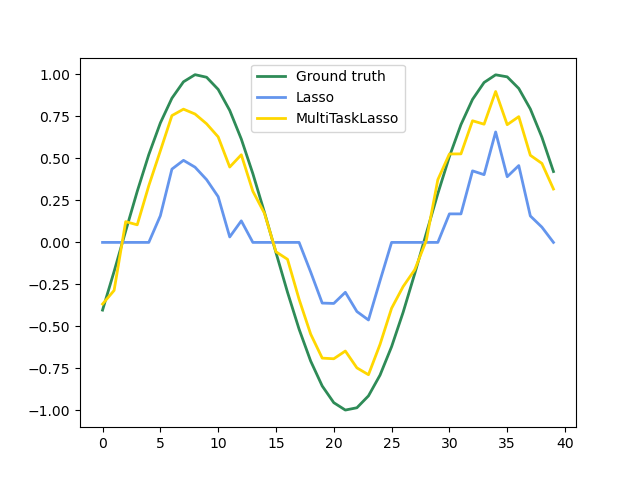
1.1.4. Многозадачный Lasso

The MultiTaskLasso является линейной моделью, которая оценивает разреженные коэффициенты для множественных задач регрессии совместно: y является двумерным массивом формы (n_samples, n_tasks). Ограничение состоит в том, что выбранные признаки одинаковы для всех задач регрессии, также называемых заданиями.

Следующий рисунок сравнивает расположение ненулевых элементов в матрице коэффициентов W, полученной с помощью простого Lasso или MultiTaskLasso. Оценки Lasso дают разрозненные ненулевые элементы, в то время как ненулевые элементы MultiTaskLasso представляют собой полные столбцы.

Обучение модели временных рядов с требованием, чтобы любой активный признак был активен всё время.

Примеры

• Совместный отбор признаков с многозадачным Lasso

Математические детали

Математически он состоит из линейной модели, обученной со смешанным \(\ell_1\) \(\ell_2\)-норма для регуляризации. Целевая функция для минимизации:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}} ^ 2 + \alpha ||W||_{21}}\]

где \(\text{Fro}\) обозначает норму Фробениуса

\[||A||_{\text{Fro}} = \sqrt{\sum_{ij} a_{ij}^2}\]

и \(\ell_1\) \(\ell_2\) читает

\[||A||_{2 1} = \sum_i \sqrt{\sum_j a_{ij}^2}.\]

Реализация в классе MultiTaskLasso использует координатный спуск в качестве алгоритма для подгонки коэффициентов.

1.1.5. Elastic-Net

ElasticNet — это модель линейной регрессии, обученная с использованием как \(\ell_1\) и \(\ell_2\)-норма регуляризации коэффициентов. Эта комбинация позволяет обучать разреженную модель, где немногие из весов ненулевые, как Lasso, сохраняя при этом регуляризационные свойства Ridge. Мы управляем выпуклой комбинацией \(\ell_1\) и \(\ell_2\) используя l1_ratio параметр.

Elastic-net полезен, когда есть несколько коррелирующих друг с другом признаков. Lasso, вероятно, выберет один из них случайным образом, в то время как elastic-net, вероятно, выберет оба.

Практическое преимущество компромисса между Lasso и Ridge заключается в том, что он позволяет Elastic-Net унаследовать некоторую стабильность Ridge при вращении.

Целевая функция для минимизации в этом случае

\[\min_{w} { \frac{1}{2n_{\text{samples}}} ||X w - y||_2 ^ 2 + \alpha \rho ||w||_1 + \frac{\alpha(1-\rho)}{2} ||w||_2 ^ 2}\]

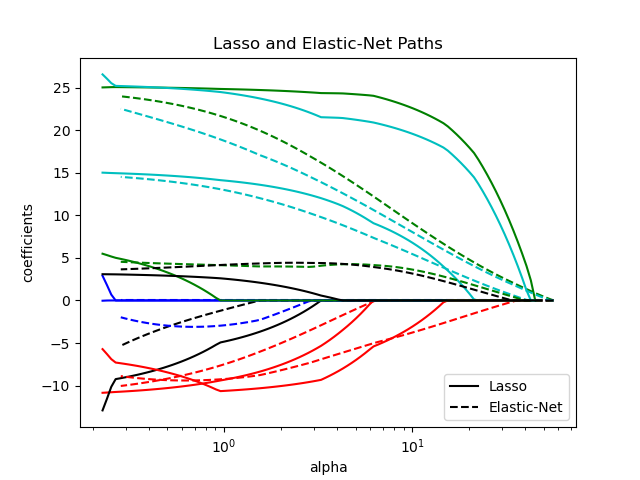
Класс ElasticNetCV можно использовать для установки параметров alpha (\(\alpha\)) и l1_ratio (\(\rho\)) с помощью перекрёстной проверки.

Примеры

• Модели на основе L1 для разреженных сигналов

• Пути Lasso, Lasso-LARS и Elastic Net

• Обучение Elastic Net с предвычисленной матрицей Грама и взвешенными выборками

Ссылки

Следующие две ссылки объясняют итерации, используемые в решателе координатного спуска scikit-learn, а также вычисление двойственного разрыва, используемое для контроля сходимости.

• “Регуляризационный путь для обобщенных линейных моделей методом координатного спуска”, Фридман, Хасти и Тибширани, J Stat Softw, 2010 (Статья).

• “Метод внутренней точки для крупномасштабных L1-регуляризованных наименьших квадратов,” С. Дж. Ким, К. Ко, М. Лустиг, С. Бойд и Д. Гориневский, в IEEE Journal of Selected Topics in Signal Processing, 2007 (Статья)

1.1.6. Многозадачный Elastic-Net

The MultiTaskElasticNet — это модель elastic-net, которая совместно оценивает разреженные коэффициенты для множественных задач регрессии: Y является двумерным массивом формы (n_samples, n_tasks). Ограничение состоит в том, что выбранные признаки одинаковы для всех задач регрессии, также называемых заданиями.

Математически он состоит из линейной модели, обученной со смешанным \(\ell_1\) \(\ell_2\)-норма и \(\ell_2\)-норма для регуляризации. Целевая функция для минимизации:

\[\min_{W} { \frac{1}{2n_{\text{samples}}} ||X W - Y||_{\text{Fro}}^2 + \alpha \rho ||W||_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||_{\text{Fro}}^2}\]

Реализация в классе MultiTaskElasticNet использует координатный спуск как алгоритм для подгонки коэффициентов.

Класс MultiTaskElasticNetCV можно использовать для установки параметров alpha (\(\alpha\)) и l1_ratio (\(\rho\)) с помощью перекрёстной проверки.

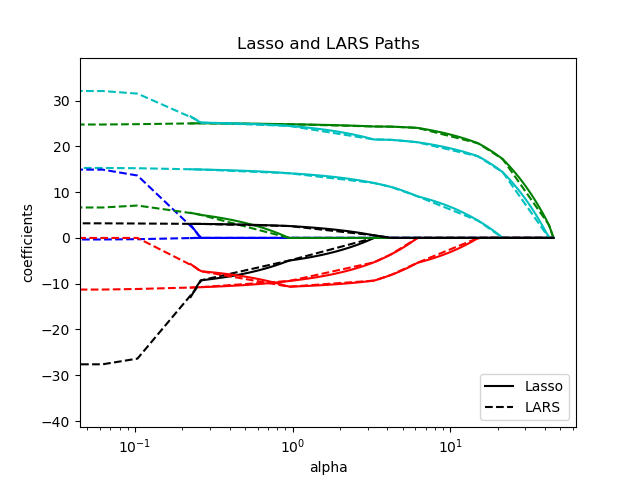
1.1.7. Least Angle Regression

Регрессия с наименьшими углами (LARS) — это алгоритм регрессии для данных высокой размерности, разработанный Брэдли Эфроном, Тревором Хасти, Иэном Джонстоном и Робертом Тибширани. LARS похож на пошаговую регрессию вперёд. На каждом шаге он находит признак, наиболее коррелированный с целью. Когда есть несколько признаков с одинаковой корреляцией, вместо продолжения вдоль того же признака он движется в направлении, равноугольном между признаками.

Преимущества LARS:

• Он численно эффективен в контекстах, где количество признаков значительно больше количества образцов.

• Вычислительно так же быстра, как прямой отбор, и имеет тот же порядок сложности, что и обычный метод наименьших квадратов.

• Он создает полный кусочно-линейный путь решения, что полезно при перекрестной проверке или подобных попытках настройки модели.

• Если две функции почти одинаково коррелируют с целью, то их коэффициенты должны увеличиваться примерно с одинаковой скоростью. Алгоритм ведет себя так, как ожидает интуиция, а также является более стабильным.

• Его легко модифицировать для получения решений для других оценщиков, таких как Lasso.

Недостатки метода LARS включают:

• Поскольку LARS основан на итеративном переобучении остатков, он, по-видимому, особенно чувствителен к эффектам шума. Эта проблема подробно обсуждается Вайсбергом в разделе обсуждения статьи Эфрона и др. (2004) в Annals of Statistics.

Модель LARS может быть использована через оценщик Larsили его низкоуровневая реализация lars_path или lars_path_gram.

1.1.8. LARS Lasso

LassoLars — это модель лассо, реализованная с использованием алгоритма LARS, и в отличие от реализации на основе покоординатного спуска, это дает точное решение, которое является кусочно-линейным как функция от нормы его коэффициентов.

>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1)
>>> reg.coef_
array([0.6, 0.        ])

Примеры

• Пути Lasso, Lasso-LARS и Elastic Net

Алгоритм LARS предоставляет полный путь коэффициентов вдоль параметра регуляризации практически бесплатно, поэтому обычная операция — получить путь с помощью одной из функций lars_path или lars_path_gram.

Математическая формулировка

Алгоритм похож на пошаговую прямую регрессию, но вместо включения признаков на каждом шаге, расчетные коэффициенты увеличиваются в направлении, равноугольном корреляциям каждого из них с остатком.

Вместо возврата векторного результата, решение LARS представляет собой кривую, обозначающую решение для каждого значения \(\ell_1\) норма вектора параметров. Полный путь коэффициентов хранится в массиве coef_path_ формы (n_features, max_features + 1)Первый столбец всегда равен нулю.

Ссылки

• Оригинальный алгоритм подробно описан в статье Least Angle Regression от Hastie et al.

1.1.9. Ортогональное согласованное преследование (OMP)

OrthogonalMatchingPursuit и orthogonal_mp реализует алгоритм OMP для аппроксимации соответствия линейной модели с ограничениями, наложенными на количество ненулевых коэффициентов (т.е. \(\ell_0\) псевдонорма).

Будучи методом прямого отбора признаков, таким как Least Angle Regression, ортогональный жадный поиск может аппроксимировать оптимальный вектор решения с фиксированным количеством ненулевых элементов:

\[\underset{w}{\operatorname{arg\,min\,}} ||y - Xw||_2^2 \text{ subject to } ||w||_0 \leq n_{\text{nonzero_coefs}}\]

В качестве альтернативы, ортогональный поиск по совпадениям может нацеливаться на конкретную ошибку вместо конкретного количества ненулевых коэффициентов. Это можно выразить как:

\[\underset{w}{\operatorname{arg\,min\,}} ||w||_0 \text{ subject to } ||y-Xw||_2^2 \leq \text{tol}\]

OMP основан на жадном алгоритме, который на каждом шаге включает атом, наиболее сильно коррелированный с текущим остатком. Он похож на более простой метод поиска совпадений (MP), но лучше тем, что на каждой итерации остаток пересчитывается с использованием ортогональной проекции на пространство ранее выбранных элементов словаря.

Примеры

• Orthogonal Matching Pursuit

Ссылки

• https://www.cs.technion.ac.il/~ronrubin/Publications/KSVD-OMP-v2.pdf

• Matching pursuits with time-frequency dictionaries, S. G. Mallat, Z. Zhang, 1993.

1.1.10. Байесовская регрессия

Байесовские методы регрессии могут использоваться для включения параметров регуляризации в процедуру оценки: параметр регуляризации не устанавливается жестко, а настраивается на основе данных.

Это можно сделать, введя неинформативные априорные распределения по гиперпараметрам модели. Класс \(\ell_{2}\) регуляризация, используемая в Ридж-регрессия и классификация эквивалентно нахождению оценки максимального апостериорного распределения при гауссовском априорном распределении над коэффициентами \(w\) с точностью \(\lambda^{-1}\). Вместо установки lambda вручную, возможно рассматривать его как случайную переменную, которую нужно оценить по данным.

Чтобы получить полностью вероятностную модель, выход \(y\) предполагается распределённым по Гауссу вокруг \(X w\):

\[p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha^{-1})\]

где \(\alpha\) снова рассматривается как случайная величина, которую нужно оценить по данным.

Преимущества байесовской регрессии:

• Он адаптируется к имеющимся данным.

• Это может использоваться для включения параметров регуляризации в процедуру оценки.

Недостатки байесовской регрессии включают:

• Вывод модели может быть трудоёмким.

Ссылки

• Хорошее введение в байесовские методы дано в C. Bishop: Pattern Recognition and Machine Learning.

• Оригинальный алгоритм подробно описан в книге Байесовское обучение для нейронных сетей от Radford M. Neal.

1.1.10.1. Байесовская гребневая регрессия

BayesianRidge оценивает вероятностную модель регрессионной задачи, как описано выше. Априорное распределение для коэффициента \(w\) задаётся сферическим гауссовым распределением:

\[p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}_{p})\]

Априорные распределения над \(\alpha\) и \(\lambda\) выбираются для гамма распределения, сопряженный априор для точности Гаусса. Полученная модель называется Байесовская гребневая регрессия, и похож на классический Ridge.

Параметры \(w\), \(\alpha\) и \(\lambda\) оцениваются совместно во время обучения модели, параметры регуляризации \(\alpha\) и \(\lambda\) оценивается путём максимизации логарифм маргинального правдоподобия. Реализация scikit-learn основана на алгоритме, описанном в Приложении A (Tipping, 2001), где обновление параметров \(\alpha\) и \(\lambda\) выполняется как предложено в (MacKay, 1992). Начальное значение процедуры максимизации может быть установлено с помощью гиперпараметров alpha_init и lambda_init.

Есть еще четыре гиперпараметра, \(\alpha_1\), \(\alpha_2\), \(\lambda_1\) и \(\lambda_2\) гамма-априорных распределений над \(\alpha\) и \(\lambda\). Обычно они выбираются как неинформативный. По умолчанию \(\alpha_1 = \alpha_2 = \lambda_1 = \lambda_2 = 10^{-6}\).

Байесовская гребневая регрессия используется для регрессии:

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()

После обучения модель может использоваться для предсказания новых значений:

>>> reg.predict([[1, 0.]])
array([0.50000013])

Коэффициенты \(w\) модели может быть доступен:

>>> reg.coef_
array([0.49999993, 0.49999993])

Из-за байесовского подхода найденные веса немного отличаются от найденных с помощью Метод наименьших квадратовОднако байесовская гребневая регрессия более устойчива к некорректно поставленным задачам.

Примеры

• Аппроксимация кривой с использованием байесовской гребневой регрессии

Ссылки

• Раздел 3.3 в Christopher M. Bishop: Pattern Recognition and Machine Learning, 2006

• David J. C. MacKay, Байесовская интерполяция, 1992.

• Michael E. Tipping, Разреженное байесовское обучение и релевантная векторная машина, 2001.

1.1.10.2. Автоматическое определение релевантности - ARD

Автоматическое определение релевантности (как реализовано в ARDRegression) — это вид линейной модели, который очень похож на Байесовская гребневая регрессия, но это приводит к более разреженным коэффициентам \(w\) [1] [2].

ARDRegression предполагает другой априор над \(w\): он заменяет сферическое гауссовское распределение на центрированное эллиптическое гауссовское распределение. Это означает, что каждый коэффициент \(w_{i}\) может быть взят из гауссовского распределения, центрированного на нуле и с точностью \(\lambda_{i}\):

\[p(w|\lambda) = \mathcal{N}(w|0,A^{-1})\]

с \(A\) является положительно определенной диагональной матрицей и \(\text{diag}(A) = \lambda = \{\lambda_{1},...,\lambda_{p}\}\).

В отличие от Байесовская гребневая регрессия, каждая координата \(w_{i}\) имеет собственное стандартное отклонение \(\frac{1}{\lambda_i}\). Априорное распределение по всем \(\lambda_i\) выбирается таким же гамма-распределением, заданным гиперпараметрами \(\lambda_1\) и \(\lambda_2\).

может казаться бинарным. Разреженное байесовское обучение и Машина опорных векторов релевантности [3] [4].

См. Сравнение линейных байесовских регрессоров для подробного сравнения между ARD и Байесовская гребневая регрессия.

См. Модели на основе L1 для разреженных сигналов для сравнения различных методов - Lasso, ARD и ElasticNet - на коррелированных данных.

Ссылки

[1]

Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 7.2.1

[2]

Дэвид Випф и Шрикантан Нагараджан: Новый взгляд на автоматическое определение релевантности

[3]

Michael E. Tipping: Разреженное байесовское обучение и релевантная векторная машина

[4]

Тристан Флетчер: Объяснение машин опорных векторов релевантности

1.1.11. Логистическая регрессия

Логистическая регрессия реализована в LogisticRegression. Несмотря на своё название, он реализован как линейная модель для классификации, а не регрессии, в терминах номенклатуры scikit-learn/ML. Логистическая регрессия также известна в литературе как регрессия logit, классификация с максимальной энтропией (MaxEnt) или log-linear классификатор. В этой модели вероятности, описывающие возможные исходы одного испытания, моделируются с использованием логистической функции.

Эта реализация может обучать бинарную, One-vs-Rest или мультиномиальную логистическую регрессию с опциональным \(\ell_1\), \(\ell_2\) или регуляризация Elastic-Net.

Примечание

Регуляризация

Регуляризация применяется по умолчанию, что распространено в машинном обучении, но не в статистике. Еще одно преимущество регуляризации — улучшение численной устойчивости. Отсутствие регуляризации эквивалентно установке C в очень большое значение.

Примечание

Логистическая регрессия как частный случай обобщённых линейных моделей (GLM)

Логистическая регрессия — это частный случай Обобщенные линейные модели с биномиальным / бернуллиевским условным распределением и логит-связью. Числовой вывод логистической регрессии, который является предсказанной вероятностью, может использоваться как классификатор путём применения порога (по умолчанию 0.5) к нему. Именно так это реализовано в scikit-learn, поэтому он ожидает категориальную цель, делая логистическую регрессию классификатором.

Примеры

• L1-штраф и разреженность в логистической регрессии

• Регуляризационный путь L1-логистической регрессии

• Границы решений мультиномиальной и логистической регрессии One-vs-Rest

• Многоклассовая разреженная логистическая регрессия на 20newsgroups

• Классификация MNIST с использованием мультиномиальной логистической регрессии + L1

• Построить график вероятности классификации

1.1.11.1. Бинарный случай

Для удобства обозначений предположим, что целевая переменная \(y_i\) принимает значения в множестве \(\{0, 1\}\) для точки данных \(i\). После обучения, predict_proba метод LogisticRegression предсказывает вероятность положительного класса \(P(y_i=1|X_i)\) как

\[\hat{p}(X_i) = \operatorname{expit}(X_i w + w_0) = \frac{1}{1 + \exp(-X_i w - w_0)}.\]

Как задача оптимизации, бинарная логистическая регрессия с регуляризационным членом \(r(w)\) минимизирует следующую функцию стоимости:

(1)\[\min_{w} \frac{1}{S}\sum_{i=1}^n s_i \left(-y_i \log(\hat{p}(X_i)) - (1 - y_i) \log(1 - \hat{p}(X_i))\right) + \frac{r(w)}{S C}\,,\]

где \({s_i}\) соответствует весам, назначенным пользователем для конкретной обучающей выборки (вектор \(s\) формируется поэлементным умножением весов классов и весов образцов), и сумма \(S = \sum_{i=1}^n s_i\).

В настоящее время мы предоставляем четыре варианта регуляризации или штрафного члена \(r(w)\) через аргументы C и l1_ratio:

штраф	\(r(w)\)
none (C=np.inf)	\(0\)
\(\ell_1\) (l1_ratio=1)	\(\|w\|_1\)
\(\ell_2\) (l1_ratio=0)	\(\frac{1}{2}\|w\|_2^2 = \frac{1}{2}w^T w\)
ElasticNet (0)	\(\frac{1 - \rho}{2}w^T w + \rho \|w\|_1\)

Для ElasticNet, \(\rho\) (что соответствует l1_ratio параметр) контролирует силу \(\ell_1\) регуляризация против. \(\ell_2\) регуляризация. Elastic-Net эквивалентен \(\ell_1\) когда \(\rho = 1\) и эквивалентно \(\ell_2\) когда \(\rho=0\).

Обратите внимание, что масштаб весов классов и весов выборок повлияет на задачу оптимизации. Например, умножение весов выборок на константу \(b>0\) эквивалентно умножению (обратной) силы регуляризации C by \(b\).

1.1.11.2. Мультиномиальный случай

Бинарный случай может быть расширен до \(K\) классы, ведущие к мультиномиальной логистической регрессии, см. также логарифмически-линейная модель.

Примечание

Можно параметризовать \(K\)-классовая модель классификации, использующая только \(K-1\) векторы весов, оставляя вероятность одного класса полностью определенной вероятностями других классов, используя тот факт, что все вероятности классов должны суммироваться в единицу. Мы сознательно выбираем перепараметризацию модели с помощью \(K\) векторы весов для удобства реализации и сохранения симметричного индуктивного смещения относительно порядка классов, см. [16]. Этот эффект становится особенно важным при использовании регуляризации. Выбор перепараметризации может быть вредным для нештрафованных моделей, поскольку тогда решение может быть не единственным, как показано в [16].

Математические детали

Пусть \(y_i \in \{1, \ldots, K\}\) будет целевой переменной (ординальной) с кодировкой меток для наблюдения \(i\). \(W\) где каждый вектор строки \(W_k\) соответствует классу \(k\). Мы стремимся предсказать вероятности классов \(P(y_i=k|X_i)\) через predict_proba как:

\[\hat{p}_k(X_i) = \frac{\exp(X_i W_k + W_{0, k})}{\sum_{l=0}^{K-1} \exp(X_i W_l + W_{0, l})}.\]

Целевая функция для оптимизации становится

\[\min_W -\frac{1}{S}\sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik} [y_i = k] \log(\hat{p}_k(X_i)) + \frac{r(W)}{S C}\,,\]

где \([P]\) представляет скобку Айверсона, которая вычисляется в \(0\) if \(P\) ложно, в противном случае вычисляется как \(1\).

Опять же, \(s_{ik}\) это веса, назначенные пользователем (произведение весов образцов и весов классов) с их суммой \(S = \sum_{i=1}^n \sum_{k=0}^{K-1} s_{ik}\).

В настоящее время мы предоставляем четыре варианта регуляризации или штрафного члена \(r(W)\) через аргументы C и l1_ratio, где \(m\) — это количество признаков:

штраф	\(r(W)\)
none (C=np.inf)	\(0\)
\(\ell_1\) (l1_ratio=1)	\(\|W\|_{1,1} = \sum_{i=1}^m\sum_{j=1}^{K}|W_{i,j}|\)
\(\ell_2\) (l1_ratio=0)	\(\frac{1}{2}\|W\|_F^2 = \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^{K} W_{i,j}^2\)
ElasticNet (0)	\(\frac{1 - \rho}{2}\|W\|_F^2 + \rho \|W\|_{1,1}\)

1.1.11.3. Решатели

Решатели, реализованные в классе LogisticRegression это "lbfgs", "liblinear", "newton-cg", "newton-cholesky", "sag" и "saga":

Следующая таблица суммирует штрафы и многоклассовую мультиномиальную классификацию, поддерживаемые каждым решателем:

	Решатели
Штрафы	'lbfgs'	'liblinear'		‘newton-cg’	Как было сказано ранее, "положительная метка" не определена как значение "1", и вызов некоторых метрик с этим нестандартным значением вызывает ошибку. Нам нужно указать "положительную метку" для метрик.	'sag'	‘saga’
Штраф L2	да	да		да	да	да	да
Штраф L1	нет	да		нет	нет	нет	да
Elastic-Net (L1 + L2)	нет	нет		нет	нет	нет	да
Без штрафа	да	нет		да	да	да	да
Поддержка многоклассовой классификации
мультиномиальная многоклассовая классификация	да	нет		да	да	да	да
Поведения
Штрафовать свободный член (плохо)	нет	да		нет	нет	нет	нет
Быстрее для больших наборов данных	нет	нет		нет	нет	да	да
Устойчив к не масштабированным наборам данных	да	да		да	да	нет	нет

Решатель "lbfgs" используется по умолчанию из-за его надежности. Для n_samples >> n_features, "newton-cholesky" является хорошим выбором и может достигать высокой точности (крошечной tol значения). Для больших наборов данных решатель "saga" обычно быстрее (чем "lbfgs"), особенно для низкой точности (высокий tol). Для больших наборов данных вы также можете рассмотреть использование SGDClassifier с loss="log_loss", что может быть даже быстрее, но требует больше настройки.

1.1.11.3.1. Различия между решателями

Может быть разница в полученных баллах между LogisticRegression с solver=liblinear или LinearSVC и внешнюю библиотеку liblinear напрямую, когда fit_intercept=False и метод fit coef_ (или) данные для предсказания являются нулями. Это происходит потому, что для выборки(ок) с decision_function ноль, LogisticRegression и LinearSVC предсказывает отрицательный класс, в то время как liblinear предсказывает положительный класс. Обратите внимание, что модель с fit_intercept=False и имея много образцов с decision_function ноль, вероятно, является недообученной, плохой моделью, и рекомендуется установить fit_intercept=True и увеличить intercept_scaling.

Детали решателей

• Решатель "liblinear" использует алгоритм координатного спуска (CD) и опирается на отличную C++ библиотека LIBLINEAR, который поставляется с scikit-learn. Однако алгоритм CD, реализованный в liblinear, не может обучить истинную мультиномиальную (многоклассовую) модель. Если вы все еще хотите использовать 'liblinear' для многоклассовых задач, вы можете использовать схему 'один против остальных' OneVsRestClassifier(LogisticRegression(solver="liblinear")), см. :class:`~sklearn.multiclass.OneVsRestClassifier. Обратите внимание, что минимизация мультиномиальной функции потерь, как ожидается, даёт лучше калиброванные результаты по сравнению со схемой "один против остальных". Для \(\ell_1\) регуляризация sklearn.svm.l1_min_c позволяет рассчитать нижнюю границу для C, чтобы получить не "нулевую" (все веса признаков равны нулю) модель.

• Решатели "lbfgs", "newton-cg", "newton-cholesky" и "sag" поддерживают только \(\ell_2\) регуляризация или отсутствие регуляризации, и они сходятся быстрее для некоторых высокоразмерных данных. Эти решатели (и "saga") изучают настоящую модель мультиномиальной логистической регрессии [5].

• Решатель “sag” использует стохастический градиентный спуск со средним градиентом [6]. Он быстрее чем другие решатели для больших наборов данных, когда и количество образцов, и количество признаков велико.

• Решатель "saga" [7] является вариантом "sag", который также поддерживает негладкую \(\ell_1\) штраф (l1_ratio=1). Поэтому это предпочтительный решатель для разреженной мультиномиальной логистической регрессии. Это также единственный решатель, поддерживающий Elastic-Net (0 < l1_ratio < 1).

• «lbfgs» — это алгоритм оптимизации, который аппроксимирует алгоритм Бройдена-Флетчера-Гольдфарба-Шанно [8], который относится к квази-ньютоновским методам. Как таковой, он может работать с широким диапазоном различных обучающих данных и поэтому является решателем по умолчанию. Однако его производительность страдает на плохо масштабированных наборах данных и на наборах данных с one-hot кодированными категориальными признаками с редкими категориями.

• Решатель «newton-cholesky» — это точный решатель Ньютона, который вычисляет матрицу Гессе и решает полученную линейную систему. Это очень хороший выбор для n_samples >> n_features и может достигать высокой точности (малые значения tol), но имеет несколько недостатков: Только \(\ell_2\) регуляризация поддерживается. Кроме того, поскольку матрица Гессе вычисляется явно, использование памяти имеет квадратичную зависимость от n_features а также на n_classes.

Для сравнения некоторых из этих решателей см. [9].

Ссылки

[5]

Кристофер М. Бишоп: Распознавание образов и машинное обучение, Глава 4.3.4

[6]

Mark Schmidt, Nicolas Le Roux, и Francis Bach: Минимизация конечных сумм со стохастическим усреднённым градиентом.

[7]

Aaron Defazio, Francis Bach, Simon Lacoste-Julien: SAGA: Быстрый инкрементальный градиентный метод с поддержкой несильно выпуклых составных целевых функций.

[8]

https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm

[9]

Thomas P. Minka “Сравнение численных оптимизаторов для логистической регрессии”

[16] (1,2)

Саймон, Ноа, Дж. Фридман и Т. Хасти. «A Blockwise Descent Algorithm for Group-penalized Multiresponse and Multinomial Regression.»

Примечание

Отбор признаков с разреженной логистической регрессией

Логистическая регрессия с \(\ell_1\) штраф дает разреженные модели и, следовательно, может использоваться для выполнения отбора признаков, как подробно описано в Отбор признаков на основе L1.

Примечание

Оценка P-значения

Можно получить p-значения и доверительные интервалы для коэффициентов в случаях регрессии без регуляризации. пакет statsmodels изначально поддерживает это. Внутри sklearn можно также использовать бутстрапинг.

LogisticRegressionCV реализует Логистическую регрессию со встроенной поддержкой кросс-валидации для нахождения оптимального C и l1_ratio параметры в соответствии с scoring атрибут. Решатели “newton-cg”, “sag”, “saga” и “lbfgs” оказываются быстрее для высокоразмерных плотных данных благодаря тёплому старту (см. Глоссарий).

1.1.12. Обобщенные линейные модели

Обобщенные линейные модели (GLM) расширяют линейные модели двумя способами [10]. Во-первых, предсказанные значения \(\hat{y}\) связаны с линейной комбинацией входных переменных \(X\) через обратную функцию связи \(h\) как

\[\hat{y}(w, X) = h(Xw).\]

Во-вторых, квадратичная функция потерь заменяется на единичное отклонение \(d\) распределения в экспоненциальном семействе (или, точнее, репродуктивной экспоненциальной дисперсионной модели (EDM) [11]).

Задача минимизации становится:

\[\min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} ||w||_2^2,\]

где \(\alpha\) - это штраф L2-регуляризации. Когда предоставляются веса выборок, среднее становится взвешенным средним.

Следующая таблица перечисляет некоторые конкретные EDMs и их единичные отклонения:

Распределение	Целевая область	Единичное отклонение \(d(y, \hat{y})\)
Нормальный	\(y \in (-\infty, \infty)\)	\((y-\hat{y})^2\)
Bernoulli	\(y \in \{0, 1\}\)	\(2({y}\log\frac{y}{\hat{y}}+({1}-{y})\log\frac{{1}-{y}}{{1}-\hat{y}})\)
Категориальный	\(y \in \{0, 1, ..., k\}\)	\(2\sum_{i \in \{0, 1, ..., k\}} I(y = i) y_\text{i}\log\frac{I(y = i)}{\hat{I(y = i)}}\)
Пуассон	\(y \in [0, \infty)\)	\(2(y\log\frac{y}{\hat{y}}-y+\hat{y})\)
Gamma	\(y \in (0, \infty)\)	\(2(\log\frac{\hat{y}}{y}+\frac{y}{\hat{y}}-1)\)
Обратное гауссовское распределение	\(y \in (0, \infty)\)	\(\frac{(y-\hat{y})^2}{y\hat{y}^2}\)

Функции плотности вероятности (PDF) этих распределений показаны на следующем рисунке,

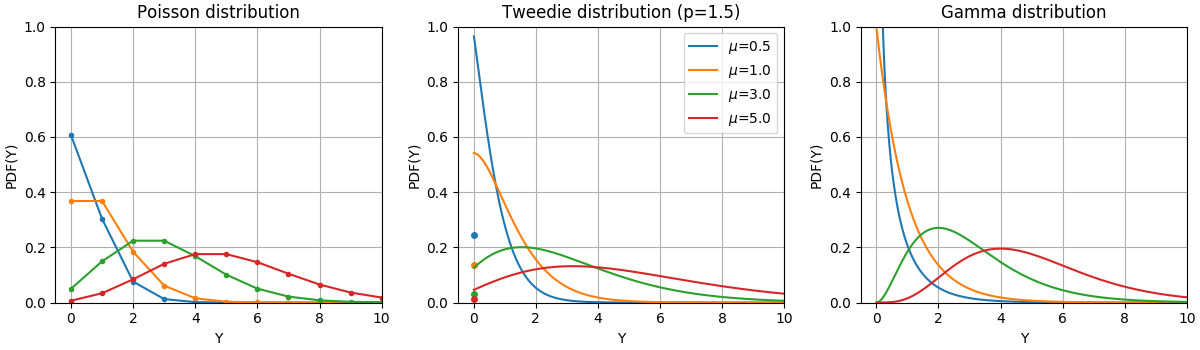
PDF случайной величины Y, следующей распределениям Пуассона, Твиди (степень=1.5) и Гамма с разными средними значениями (\(\mu\)). Обратите внимание на точечную массу в \(Y=0\) для распределения Пуассона и распределения Твиди (power=1.5), но не для гамма-распределения, которое имеет строго положительную область значений.

Распределение Бернулли — это дискретное распределение вероятностей, моделирующее испытание Бернулли — событие, имеющее только два взаимоисключающих исхода. Категориальное распределение является обобщением распределения Бернулли для категориальной случайной величины. В то время как случайная величина в распределении Бернулли имеет два возможных исхода, категориальная случайная величина может принимать одно из K возможных категорий, с вероятностью каждой категории, указанной отдельно.

Выбор распределения зависит от конкретной задачи:

• Если целевые значения \(y\) являются подсчетами (неотрицательные целочисленные значения) или относительными частотами (неотрицательные), вы можете использовать распределение Пуассона с логарифмической связью.

• Если целевые значения положительны и асимметричны, вы можете попробовать гамма-распределение с логарифмической связью.

• Если целевые значения имеют более тяжёлые хвосты, чем гамма-распределение, вы можете попробовать обратное гауссово распределение (или даже более высокие степени дисперсии семейства Твиди).

• Если целевые значения \(y\) являются вероятностями, вы можете использовать распределение Бернулли. Распределение Бернулли с логит-связью может использоваться для бинарной классификации. Категориальное распределение с softmax-связью может использоваться для многоклассовой классификации.

Примеры случаев использования

• Сельское хозяйство / моделирование погоды: количество дождевых событий в год (Пуассон), количество осадков за событие (Гамма), общее количество осадков в год (Твиди / Составной Пуассон-Гамма).

• Моделирование рисков / ценообразование страховых полисов: количество страховых случаев / страхователь в год (Пуассон), стоимость на случай (Гамма), общая стоимость на страхователя в год (Твиди / Составной Пуассон-Гамма).

• Кредитный дефолт: вероятность невозврата кредита (Бернулли).

• Обнаружение мошенничества: вероятность того, что финансовая операция, такая как денежный перевод, является мошеннической транзакцией (Бернулли).

• Прогнозируемое обслуживание: количество событий прерывания производства в год (Пуассон), длительность прерывания (Гамма), общее время прерывания в год (Твиди / Составной Пуассон-Гамма).

• Медицинские испытания лекарств: вероятность излечения пациента в серии испытаний или вероятность того, что у пациента возникнут побочные эффекты (Бернулли).

• Классификация новостей: классификация новостных статей на три категории, а именно Бизнес-новости, Политика и Развлекательные новости (Категориальные).

Ссылки

[10]

McCullagh, Peter; Nelder, John (1989). Generalized Linear Models, Second Edition. Boca Raton: Chapman and Hall/CRC. ISBN 0-412-31760-5.

[11]

Jørgensen, B. (1992). The theory of exponential dispersion models and analysis of deviance. Monografias de matemática, no. 51. См. также Экспоненциальная дисперсионная модель.

1.1.12.1. Использование

TweedieRegressor реализует обобщенную линейную модель для распределения Твиди, которая позволяет моделировать любое из вышеупомянутых распределений, используя соответствующий power параметр. В частности:

• power = 0: Нормальное распределение. Специфические оценщики, такие как Ridge, ElasticNet обычно более подходят в этом случае.

• power = 1: распределение Пуассона. PoissonRegressor предоставлен для удобства. Однако он строго эквивалентен TweedieRegressor(power=1, link='log').

• power = 2: Гамма-распределение. GammaRegressor предоставлен для удобства. Однако он строго эквивалентен TweedieRegressor(power=2, link='log').

• power = 3: обратное гауссовское распределение.

Связующая функция определяется link параметр.

Пример использования:

>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463, 0.4337])
>>> reg.intercept_
np.float64(-0.7638)

Примеры

• Пуассоновская регрессия и ненормальные потери

• Регрессия Твиди для страховых случаев

Практические соображения

Матрица признаков X должны быть стандартизированы перед обучением. Это гарантирует, что штраф обрабатывает признаки одинаково.

Поскольку линейный предиктор \(Xw\) может быть отрицательным, а распределения Пуассона, Гамма и обратное Гауссово не поддерживают отрицательные значения, поэтому необходимо применять обратную функцию связи, гарантирующую неотрицательность. Например, с link='log', обратная функция связи становится \(h(Xw)=\exp(Xw)\).

Если вы хотите смоделировать относительную частоту, т.е. количество на единицу экспозиции (время, объем, ...), вы можете сделать это, используя распределение Пуассона и передав \(y=\frac{\mathrm{counts}}{\mathrm{exposure}}\) в качестве целевых значений вместе с \(\mathrm{exposure}\) в качестве весов образцов. Для конкретного примера см., например, Регрессия Твиди для страховых случаев.

При выполнении перекрестной проверки для power параметр TweedieRegressor, рекомендуется указать явный scoring функция, поскольку стандартный скорер TweedieRegressor.score является функцией от power самого себя.

1.1.13. Стохастический градиентный спуск - SGD

Стохастический градиентный спуск — это простой, но очень эффективный подход к обучению линейных моделей. Он особенно полезен, когда количество выборок (и количество признаков) очень велико. partial_fit метод позволяет обучаться онлайн/вне ядра.

Классы SGDClassifier и SGDRegressor предоставляет функциональность для подбора линейных моделей классификации и регрессии с использованием различных (выпуклых) функций потерь и различных штрафов. Например, с loss="log", SGDClassifier обучает модель логистической регрессии, в то время как с loss="hinge" он обучает линейную машину опорных векторов (SVM).

Вы можете обратиться к специальному Стохастический градиентный спуск раздел документации для получения более подробной информации.

1.1.13.1. Перцептрон

The Perceptron ещё один простой алгоритм классификации, подходящий для обучения в больших масштабах и производный от SGD. По умолчанию:

• Не требует скорости обучения.

• Он не регуляризован (не штрафуется).

• Он обновляет свою модель только на ошибках.

Последняя характеристика означает, что Перцептрон обучается немного быстрее, чем SGD с функцией потерь hinge, и результирующие модели получаются более разреженными.

На самом деле, Perceptron является оберткой вокруг SGDClassifier класс с использованием функции потерь перцептрона и постоянной скорости обучения. См. математический раздел процедуры SGD для более подробной информации.

1.1.13.2. Пассивно-агрессивные алгоритмы

Пассивно-агрессивные (PA) алгоритмы — это еще одно семейство из 2 алгоритмов (PA-I и PA-II) для крупномасштабного онлайн-обучения, производных от SGD. Они похожи на перцептрон тем, что не требуют скорости обучения. Однако, в отличие от перцептрона, они включают параметр регуляризации eta0 (\(C\) в исходной статье).

Для классификации, SGDClassifier(loss="hinge", penalty=None, learning_rate="pa1", eta0=1.0) может использоваться для PA-I или с learning_rate="pa2" для PA-II. Для регрессии, SGDRegressor(loss="epsilon_insensitive", penalty=None, learning_rate="pa1", eta0=1.0) может использоваться для PA-I или с learning_rate="pa2" для PA-II.

Ссылки

• «Онлайн-пассивно-агрессивные алгоритмы» K. Crammer, O. Dekel, J. Keshat, S. Shalev-Shwartz, Y. Singer - JMLR 7 (2006)

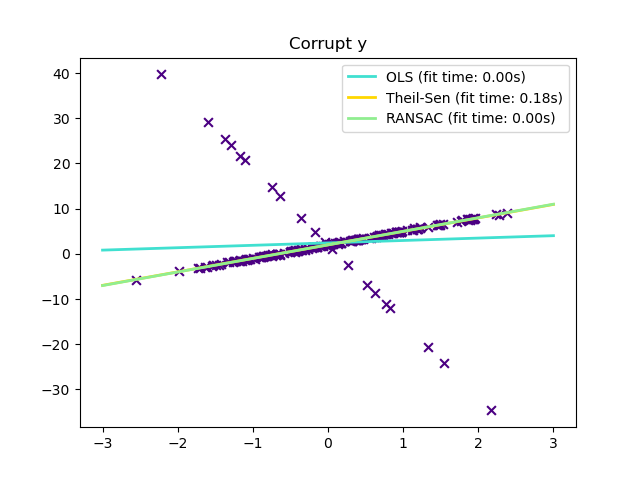
1.1.14. Робастная регрессия: выбросы и ошибки моделирования

Робастная регрессия направлена на подгонку регрессионной модели при наличии искаженных данных: либо выбросов, либо ошибок в модели.

1.1.14.1. Различные сценарии и полезные концепции

При работе с данными, искаженными выбросами, следует учитывать различные аспекты:

• Выбросы в X или в y?

  Выбросы в направлении y	Выбросы в направлении X

• Доля выбросов по сравнению с амплитудой ошибки

  Важно не только количество выбросов, но и то, насколько они являются выбросами.

  Малые выбросы	Большие выбросы

Важное понятие робастного обучения - это точка разрушения: доля данных, которые могут быть выбросами, прежде чем обучение начнет пропускать внутренние данные.

Обратите внимание, что в целом устойчивое обучение в высокоразмерных настройках (большое n_features) очень сложно. Робастные модели здесь, вероятно, не будут работать в таких условиях.

Компромиссы: какой оценщик?

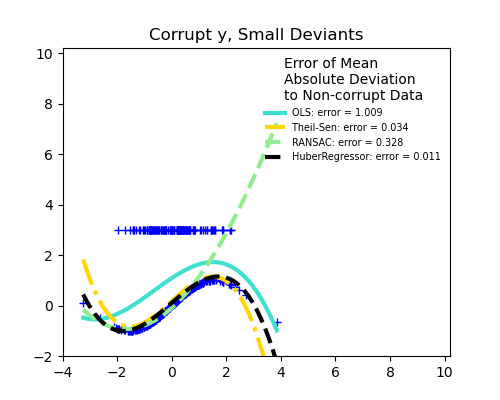
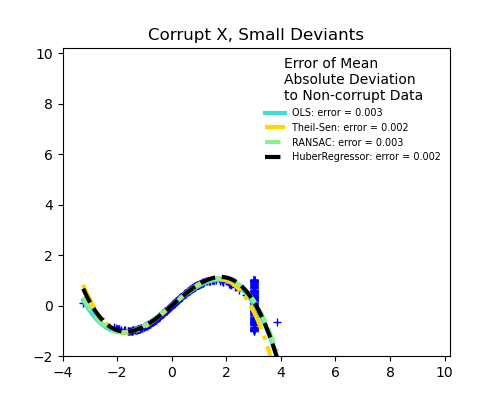
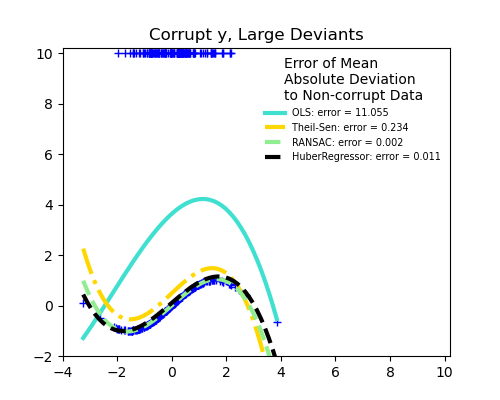
Scikit-learn предоставляет 3 робастных регрессора: RANSAC, Тейла-Сена и HuberRegressor.

• HuberRegressor должен быть быстрее, чем RANSAC и Тейла-Сена если количество выборок не очень велико, т.е. n_samples >> n_features. Это происходит потому, что RANSAC и Тейла-Сена обучение на меньших подмножествах данных. Однако оба Тейла-Сена и RANSAC вряд ли будут такими же устойчивыми, как HuberRegressor для параметров по умолчанию.

• RANSAC быстрее, чем Тейла-Сена и масштабируется гораздо лучше с увеличением количества образцов.

• RANSAC будет лучше справляться с большими выбросами в направлении y (наиболее распространенная ситуация).

• Тейла-Сена будет лучше справляться с выбросами среднего размера в направлении X, но это свойство исчезнет в многомерных настройках.

Если сомневаетесь, используйте RANSAC.

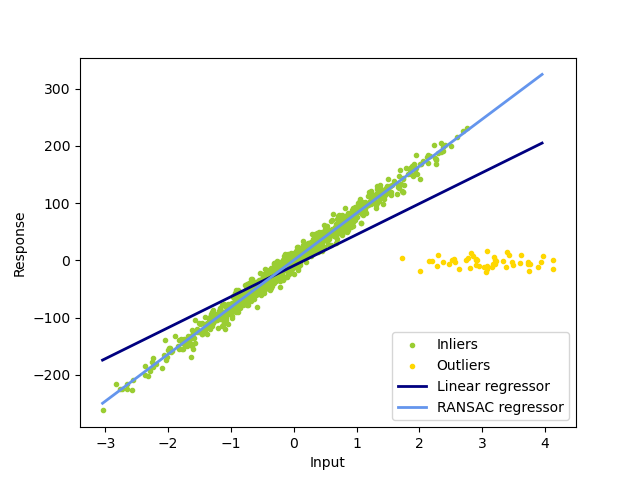
1.1.14.2. RANSAC: RANdom SAmple Consensus

RANSAC (RANdom SAmple Consensus) обучает модель на случайных подмножествах выбросов из полного набора данных.

RANSAC — это недетерминированный алгоритм, дающий только разумный результат с определенной вероятностью, которая зависит от количества итераций (см. max_trials параметр). Обычно используется для линейных и нелинейных задач регрессии и особенно популярен в области фотограмметрического компьютерного зрения.

Алгоритм разделяет полные входные данные выборки на набор выбросов, которые могут быть подвержены шуму, и аномалий, которые вызваны, например, ошибочными измерениями или неверными гипотезами о данных. Полученная модель затем оценивается только на основе определенных выбросов.

Примеры

• Робастная оценка линейной модели с использованием RANSAC

• Робастная оценка линейной модели

Детали алгоритма

Каждая итерация выполняет следующие шаги:

1. Выбрать min_samples случайные выборки из исходных данных и проверьте, является ли набор данных допустимым (см. is_data_valid).

2. Обучить модель на случайном подмножестве (estimator.fit) и проверьте, является ли оцененная модель валидной (см. is_model_valid).

3. Классифицировать все данные как нормальные или выбросы, вычисляя остатки относительно оцененной модели (estimator.predict(X) - y) - все образцы данных с абсолютными остатками, меньшими или равными residual_threshold считаются выбросами.

4. Сохранить обученную модель как лучшую, если количество выборочных объектов максимально. Если текущая оцененная модель имеет такое же количество выбросов, она считается лучшей только если имеет лучшую оценку.

Эти шаги выполняются либо максимальное количество раз (max_trials) или пока не будут выполнены специальные критерии остановки (см. stop_n_inliers и stop_score). Финальная модель оценивается с использованием всех выбросов (консенсусное множество) ранее определенной лучшей модели.

The is_data_valid и is_model_valid функции позволяют идентифицировать и отклонять вырожденные комбинации случайных подвыборок. Если оцененная модель не нужна для идентификации вырожденных случаев, is_data_valid должен использоваться, так как он вызывается перед обучением модели, что приводит к лучшей вычислительной производительности.

Ссылки

• https://en.wikipedia.org/wiki/RANSAC

• «Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography» Мартин А. Фишлер и Роберт К. Боллес - SRI International (1981)

• “Performance Evaluation of RANSAC Family” Сунглок Чой, Тэмин Ким и Вонпил Ю - BMVC (2009)

1.1.14.3. Оценщик Тейла-Сена: оценщик на основе обобщенной медианы

The TheilSenRegressor оценщик использует обобщение медианы в многомерном пространстве. Таким образом, он устойчив к многомерным выбросам. Однако учтите, что устойчивость оценщика быстро снижается с увеличением размерности задачи. Он теряет свои свойства устойчивости и становится не лучше обычного метода наименьших квадратов в высокой размерности.

Примеры

• Регрессия Тейла-Сена

• Робастная оценка линейной модели

Теоретические соображения

TheilSenRegressor сопоставим с Метод наименьших квадратов (OLS) с точки зрения асимптотической эффективности и как несмещённая оценка. В отличие от OLS, метод Тейла-Сена является непараметрическим, что означает, что он не делает предположений о базовом распределении данных. Поскольку Тейл-Сен является медианной оценкой, он более устойчив к искажённым данным, т.е. выбросам. В одномерном случае метод Тейла-Сена имеет точку разладки около 29,3% для простой линейной регрессии, что означает, что он может выдерживать произвольно искажённые данные до 29,3%.

Реализация TheilSenRegressor в scikit-learn следует обобщению на многомерную линейную регрессионную модель [14] используя пространственную медиану, которая является обобщением медианы на несколько измерений [15].

С точки временной и пространственной сложности, метод Тейла-Сена масштабируется в соответствии с

\[\binom{n_{\text{samples}}}{n_{\text{subsamples}}}\]

что делает его неприменимым для исчерпывающего использования в задачах с большим количеством выборок и признаков. Поэтому размер подвыборки может быть выбран для ограничения временной и пространственной сложности путем рассмотрения только случайного подмножества всех возможных комбинаций.

Ссылки

[14]

Xin Dang, Hanxiang Peng, Xueqin Wang и Heping Zhang: Оценщики Тейла-Сена в модели множественной линейной регрессии.

[15]

20. Kärkkäinen и S. Äyrämö: О вычислении пространственной медианы для робастного интеллектуального анализа данных.

Также см. Страница Википедии

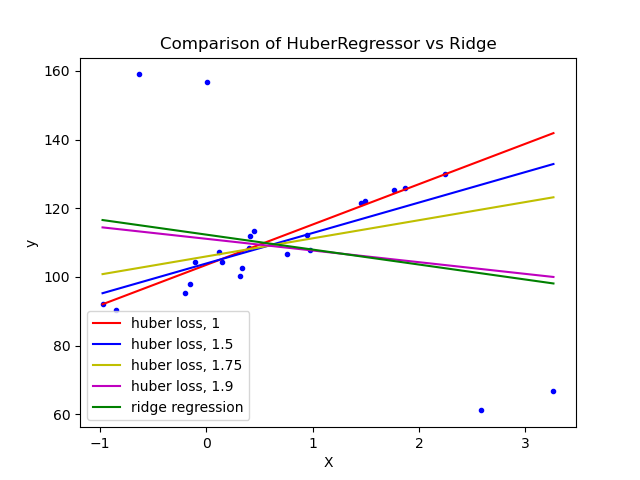
1.1.14.4. Регрессия Хубера

The HuberRegressor является многоклассовым набором данных кардиотокограмм плода, где классы представляют собой паттерны частоты сердечных сокращений плода (FHR), закодированные метками от 1 до 10. Здесь мы устанавливаем класс 3 (класс меньшинства) для представления выбросов. Он содержит 30 числовых признаков, некоторые из которых закодированы бинарно, а некоторые являются непрерывными. Ridge поскольку он применяет линейную функцию потерь к образцам, которые определены как выбросы epsilon параметр. Образец классифицируется как выброс, если абсолютная ошибка этого образца меньше порога epsilon. Он отличается от TheilSenRegressor и RANSACRegressor поскольку он не игнорирует влияние выбросов, но придает им меньший вес.

Примеры

• HuberRegressor против Ridge на наборе данных с сильными выбросами

Математические детали

HuberRegressor минимизирует

\[\min_{w, \sigma} {\sum_{i=1}^n\left(\sigma + H_{\epsilon}\left(\frac{X_{i}w - y_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||_2}^2}\]

где функция потерь задается как

\[\begin{split}H_{\epsilon}(z) = \begin{cases} z^2, & \text {if } |z| < \epsilon, \\ 2\epsilon|z| - \epsilon^2, & \text{otherwise} \end{cases}\end{split}\]

Рекомендуется установить параметр epsilon до 1.35 для достижения 95% статистической эффективности.

Ссылки

• Peter J. Huber, Elvezio M. Ronchetti: Robust Statistics, Concomitant scale estimates, p. 172.

The HuberRegressor отличается от использования SGDRegressor с loss, установленным в huber следующими способами.

• HuberRegressor инвариантен к масштабированию. Как только epsilon установлен, масштабирование X и y вниз или вверх на разные значения даст такую же устойчивость к выбросам, как и раньше. по сравнению с SGDRegressor где epsilon должен быть установлен снова, когда X и y масштабируются.

• HuberRegressor должен быть более эффективным для использования на данных с малым количеством образцов, в то время как SGDRegressor требует нескольких проходов по обучающим данным, чтобы произвести такую же надежность.

Обратите внимание, что этот оценчик отличается от R реализация устойчивой регрессии потому что реализация R выполняет взвешенную регрессию наименьших квадратов с весами, заданными для каждого образца на основе того, насколько остаток больше определенного порога.

1.1.15. Квантильная регрессия

Квантильная регрессия оценивает медиану или другие квантили \(y\) условно по \(X\), в то время как обычный метод наименьших квадратов (OLS) оценивает условное среднее.

Квантильная регрессия может быть полезна, если интересует предсказание интервала вместо точечного предсказания. Иногда интервалы предсказания рассчитываются на основе предположения, что ошибка предсказания распределена нормально с нулевым средним и постоянной дисперсией. Квантильная регрессия обеспечивает разумные интервалы предсказания даже для ошибок с непостоянной (но предсказуемой) дисперсией или ненормальным распределением.

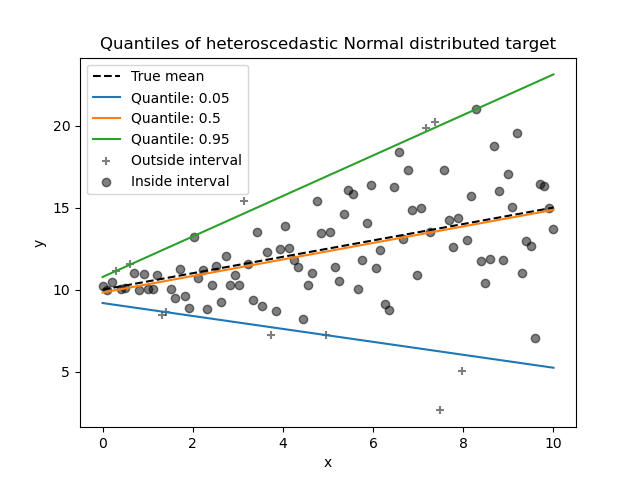
Основываясь на минимизации потерь пинбола, условные квантили также могут оцениваться моделями, отличными от линейных. Например, GradientBoostingRegressor может предсказывать условные квантили, если его параметр loss установлено в "quantile" и параметр alpha устанавливается в квантиль, который должен быть предсказан. См. пример в Интервалы прогнозирования для регрессии градиентного бустинга.

Большинство реализаций квантильной регрессии основаны на задаче линейного программирования. Текущая реализация основана на scipy.optimize.linprog.

Примеры

• Квантильная регрессия

Математические детали

Как линейная модель, QuantileRegressor дает линейные предсказания \(\hat{y}(w, X) = Xw\) для \(q\)-й квантиль, \(q \in (0, 1)\). Веса или коэффициенты \(w\) затем находятся путем следующей задачи минимизации:

\[\min_{w} {\frac{1}{n_{\text{samples}}} \sum_i PB_q(y_i - X_i w) + \alpha ||w||_1}.\]

Это включает потерю пинбола (также известную как линейная потеря), см. также mean_pinball_loss,

\[\begin{split}PB_q(t) = q \max(t, 0) + (1 - q) \max(-t, 0) = \begin{cases} q t, & t > 0, \\ 0, & t = 0, \\ (q-1) t, & t < 0 \end{cases}\end{split}\]

и штраф L1, управляемый параметром alpha, аналогично Lasso.

Поскольку пинбол-потеря линейна только по остаткам, квантильная регрессия гораздо более устойчива к выбросам, чем оценка среднего на основе квадратичной ошибки. Нечто среднее между ними — это HuberRegressor.

Ссылки

• Koenker, R., & Bassett Jr, G. (1978). Квантили регрессии. Econometrica: journal of the Econometric Society, 33-50.

• Portnoy, S., & Koenker, R. (1997). Гауссовский заяц и лапласовская черепаха: вычислимость оценок квадратичной ошибки против абсолютной ошибки. Statistical Science, 12, 279-300.

• Koenker, R. (2005). Квантильная регрессия. Cambridge University Press.

1.1.16. Полиномиальная регрессия: расширение линейных моделей с базисными функциями

Один из распространённых подходов в машинном обучении — использование линейных моделей, обученных на нелинейных функциях данных. Этот подход сохраняет общую высокую производительность линейных методов, позволяя им соответствовать гораздо более широкому диапазону данных.

Математические детали

Например, простая линейная регрессия может быть расширена путём построения полиномиальные признаки из коэффициентов. В стандартном случае линейной регрессии у вас может быть модель, которая выглядит так для двумерных данных:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2\]

Если мы хотим подогнать параболоид к данным вместо плоскости, мы можем комбинировать признаки в полиномы второго порядка, чтобы модель выглядела так:

\[\hat{y}(w, x) = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_1 x_2 + w_4 x_1^2 + w_5 x_2^2\]

(иногда удивительное) наблюдение заключается в том, что это все еще линейная модель: чтобы увидеть это, представьте создание нового набора признаков

\[z = [x_1, x_2, x_1 x_2, x_1^2, x_2^2]\]

С такой перемаркировкой данных наша задача может быть записана

\[\hat{y}(w, z) = w_0 + w_1 z_1 + w_2 z_2 + w_3 z_3 + w_4 z_4 + w_5 z_5\]

Мы видим, что полученный полиномиальная регрессия находится в том же классе линейных моделей, которые мы рассматривали выше (т.е. модель линейна по \(w\)и могут быть решены теми же методами. Рассматривая линейные подгонки в пространстве более высокой размерности, построенном с использованием этих базисных функций, модель получает гибкость для подгонки гораздо более широкого диапазона данных.

Вот пример применения этой идеи к одномерным данным с использованием полиномиальных признаков различных степеней:

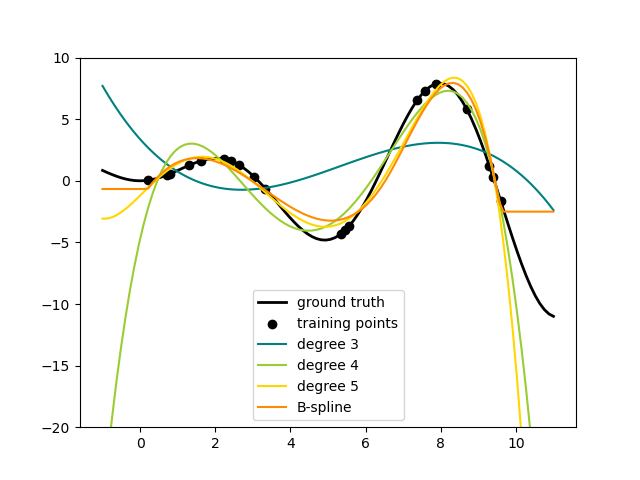
Этот рисунок создан с использованием PolynomialFeatures преобразователь, который преобразует входную матрицу данных в новую матрицу данных заданной степени. Может использоваться следующим образом:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

Признаки X были преобразованы из \([x_1, x_2]\) to \([1, x_1, x_2, x_1^2, x_1 x_2, x_2^2]\), и теперь может использоваться в любой линейной модели.

Такой тип предобработки можно упростить с помощью Pipeline инструментов. Единый объект, представляющий простую полиномиальную регрессию, может быть создан и использован следующим образом:

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

Линейная модель, обученная на полиномиальных признаках, способна точно восстановить входные полиномиальные коэффициенты.

В некоторых случаях нет необходимости включать более высокие степени любого отдельного признака, а только так называемые признаки взаимодействия которые перемножаются не более чем \(d\) различные признаки. Их можно получить из PolynomialFeatures с настройкой interaction_only=True.

Например, при работе с булевыми признаками, \(x_i^n = x_i\) для всех \(n\) и поэтому бесполезен; но \(x_i x_j\) представляет конъюнкцию двух булевых значений. Таким образом, мы можем решить проблему XOR с линейным классификатором:

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
...                  shuffle=False).fit(X, y)

И "предсказания" классификатора идеальны:

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0