2.8. Оценка плотности#
Оценка плотности находится на границе между обучением без учителя, проектированием признаков
и моделированием данных. Некоторые из самых популярных и полезных
методов оценки плотности - это модели смесей, такие как
Гауссовские смеси (GaussianMixture), и подходы на основе соседей, такие как оценка плотности ядра (KernelDensity).
Гауссовские смеси более полно обсуждаются в контексте
кластеризация, потому что эта техника также полезна как
неконтролируемая схема кластеризации.
Оценка плотности — очень простая концепция, и большинство людей уже знакомы с одной распространенной техникой оценки плотности: гистограммой.
2.8.1. Оценка плотности: Гистограммы#
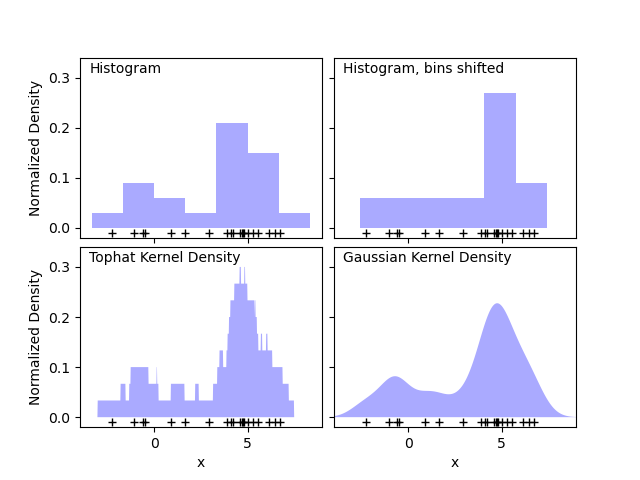
Гистограмма — это простое визуальное представление данных, где определяются бины, и подсчитывается количество точек данных в каждом бине. Пример гистограммы можно увидеть в верхней левой панели следующего рисунка:
Основная проблема с гистограммами, однако, заключается в том, что выбор бинов может иметь непропорциональный эффект на результирующую визуализацию. Рассмотрим правую верхнюю панель на рисунке выше. Она показывает гистограмму по тем же данным, со сдвинутыми вправо бинами. Результаты двух визуализаций выглядят совершенно по-разному и могут привести к разным интерпретациям данных.
Интуитивно гистограмму также можно представить как стопку блоков, по одному блоку на точку. Укладывая блоки в соответствующем пространстве сетки, мы получаем гистограмму. Но что если вместо укладки блоков на регулярную сетку мы центрируем каждый блок на представляемой им точке и суммируем общую высоту в каждом месте? Эта идея приводит к визуализации в нижнем левом углу. Возможно, она не так чиста, как гистограмма, но тот факт, что данные определяют расположение блоков, означает, что это гораздо лучшее представление исходных данных.
Эта визуализация является примером оценка плотности ядра, в данном случае с ядром в виде прямоугольной функции (т.е. квадратный блок в каждой точке). Мы можем получить более гладкое распределение, используя более гладкое ядро. График в правом нижнем углу показывает оценку плотности с гауссовым ядром, где каждая точка вносит гауссову кривую в общую сумму. Результатом является гладкая оценка плотности, которая выводится из данных и служит мощной непараметрической моделью распределения точек.
2.8.2. Оценка плотности ядра#
Оценка плотности ядра в scikit-learn реализована в
KernelDensity оценщик, который использует Ball Tree или KD Tree для эффективных запросов (см. Ближайшие соседи для
обсуждения этих вопросов). Хотя приведенный выше пример
использует одномерный набор данных для простоты, оценка плотности ядра может быть
выполнена в любом количестве измерений, хотя на практике проклятие
размерности приводит к ухудшению её производительности в высоких размерностях.
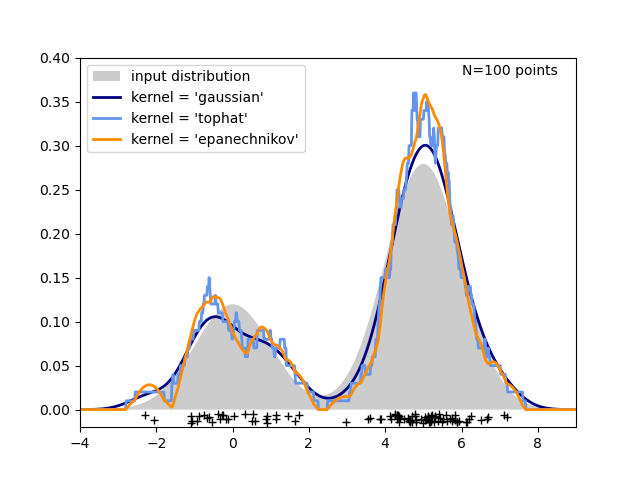
На следующем рисунке 100 точек взяты из бимодального распределения, и оценки плотности ядра показаны для трех вариантов ядер:
Понятно, как форма ядра влияет на гладкость получаемого распределения. Оценщик плотности ядра scikit-learn может быть использован следующим образом:
>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.2).fit(X)
>>> kde.score_samples(X)
array([-0.41075698, -0.41075698, -0.41076071, -0.41075698, -0.41075698,
-0.41076071])
Здесь мы использовали kernel='gaussian', как показано выше.
С математической точки зрения, ядро — это положительная функция \(K(x;h)\)
который контролируется параметром bandwidth \(h\). Учитывая эту форму ядра, оценка плотности в точке \(y\) внутри
группы точек \(x_i; i=1, \cdots, N\) задается формулой:
Полоса пропускания здесь действует как параметр сглаживания, контролируя компромисс между смещением и дисперсией в результате. Большая полоса пропускания приводит к очень гладкому (т.е. с высоким смещением) распределению плотности. Малая полоса пропускания приводит к неровному (т.е. с высокой дисперсией) распределению плотности.
Параметр bandwidth управляет этим сглаживанием. Можно либо установить этот параметр вручную, либо использовать методы оценки Скотта и Сильвермана.
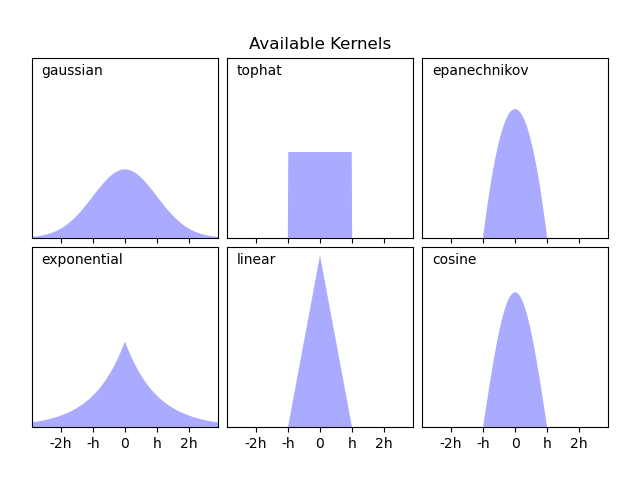
KernelDensity реализует несколько распространённых форм ядер,
которые показаны на следующем рисунке:
Математические выражения ядер#
Форма этих ядер следующая:
Гауссово ядро (
kernel = 'gaussian')\(K(x; h) \propto \exp(- \frac{x^2}{2h^2} )\)
Ядро Tophat (
kernel = 'tophat')\(K(x; h) \propto 1\) if \(x < h\)
ядро Епанечникова (
kernel = 'epanechnikov')\(K(x; h) \propto 1 - \frac{x^2}{h^2}\)
Экспоненциальное ядро (
kernel = 'exponential')\(K(x; h) \propto \exp(-x/h)\)
Линейное ядро (
kernel = 'linear')\(K(x; h) \propto 1 - x/h\) if \(x < h\)
Косинусное ядро (
kernel = 'cosine')\(K(x; h) \propto \cos(\frac{\pi x}{2h})\) if \(x < h\)
Оценщик плотности ядра может использоваться с любыми допустимыми метриками расстояния (см. DistanceMetric для списка доступных метрик), хотя результаты правильно нормализованы только для евклидовой метрики. Одна особенно полезная метрика — это
Расстояние Хаверсина
которая измеряет угловое расстояние между точками на сфере. Вот
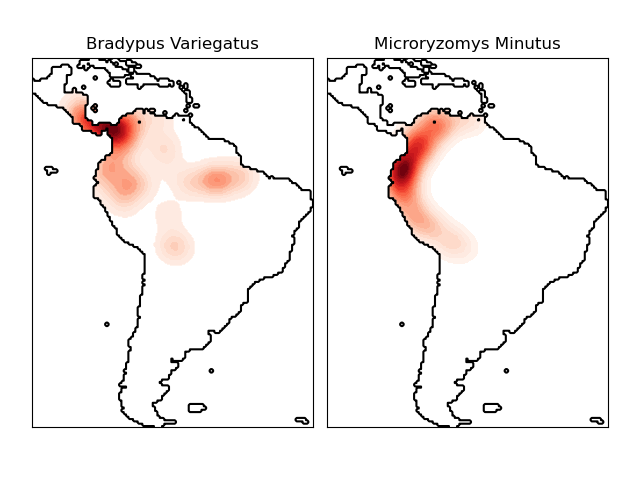
пример использования оценки плотности ядра для визуализации
геопространственных данных, в данном случае распределения наблюдений двух
разных видов на южноамериканском континенте:
Еще одно полезное применение оценки плотности ядра — это обучение непараметрической генеративной модели набора данных для эффективной генерации новых выборок из этой модели. Вот пример использования этого процесса для создания нового набора рукописных цифр с использованием гауссовского ядра, обученного на проекции данных методом главных компонент (PCA):
"Новые" данные состоят из линейных комбинаций входных данных с весами, вероятностно выбранными в соответствии с моделью KDE.
Примеры
Простое одномерное ядерное сглаживание плотности: вычисление простых оценок ядерной плотности в одном измерении.
Оценка плотности ядра: пример использования оценки плотности ядра для обучения генеративной модели данных рукописных цифр и выборки новых образцов из этой модели.
Оценка плотности ядра распределения видов: пример оценки плотности ядра с использованием метрики расстояния Haversine для визуализации геопространственных данных