1.16. Калибровка вероятностей#
При выполнении классификации часто требуется не только предсказать метку класса, но и получить вероятность соответствующей метки. Эта вероятность даёт некоторую уверенность в предсказании. Некоторые модели могут давать плохие оценки вероятностей классов, а некоторые даже не поддерживают предсказание вероятностей (например, некоторые экземпляры
SGDClassifier). Модуль калибровки позволяет лучше калибровать вероятности данной модели или добавить поддержку прогнозирования вероятностей.
Хорошо калиброванные классификаторы — это вероятностные классификаторы, для которых выход predict_proba метод может быть напрямую интерпретирован как уровень доверия. Например, хорошо калиброванный (бинарный) классификатор должен классифицировать образцы так, чтобы среди образцов, которым он дал predict_proba значение близкое к, скажем, 0.8, примерно 80% фактически принадлежат к положительному классу.
Прежде чем показать, как перекалибровать классификатор, нам сначала нужен способ определить, насколько хорошо откалиброван классификатор.
Примечание
Строго правильные правила оценки для вероятностных прогнозов, такие как
sklearn.metrics.brier_score_loss и
sklearn.metrics.log_loss оценить калибровку (надежность) и дискриминационную способность (разрешение) модели, а также случайность данных (неопределенность) одновременно. Это следует из известного разложения оценки Брайера Мерфи [1]. Поскольку неясно, какой член доминирует, оценка
имеет ограниченное применение для оценки калибровки отдельно (если не вычислять каждый член
разложения). Меньшая потеря Брайера, например, не обязательно
означает лучше откалиброванную модель, это также может означать хуже откалиброванную модель с гораздо
большей дискриминационной способностью, например, с использованием гораздо большего количества признаков.
1.16.1. Кривые калибровки#
Калибровочные кривые, также называемые диаграммы надежности (Wilks 1995 [2]), сравните, насколько хорошо откалиброваны вероятностные предсказания бинарного классификатора. Он отображает частоту положительного класса (точнее, оценку условная вероятность события \(P(Y=1|\text{predict_proba})\)) на оси y против предсказанной вероятности predict_proba модели на оси x. Сложная часть — получить значения для оси y. В scikit-learn это достигается путём бинирования предсказаний так, что ось x представляет среднюю предсказанную вероятность в каждом бине. Ось y тогда является доля положительных учитывая предсказания этого бина, т.е. долю образцов, класс которых является положительным (в каждом бине).
Верхний график калибровочной кривой создается с помощью
CalibrationDisplay.from_estimator, который использует calibration_curve для
расчета средних предсказанных вероятностей и доли положительных случаев на каждый бин.
CalibrationDisplay.from_estimator
принимает на вход обученный классификатор, который используется для вычисления предсказанных
вероятностей. Классификатор должен иметь predict_proba методом. Для
немногих классификаторов, у которых нет predict_proba метод, возможно использовать CalibratedClassifierCV для калибровки выходов классификатора в вероятности.
Нижняя гистограмма дает представление о поведении каждого классификатора, показывая количество образцов в каждом бине прогнозируемой вероятности.
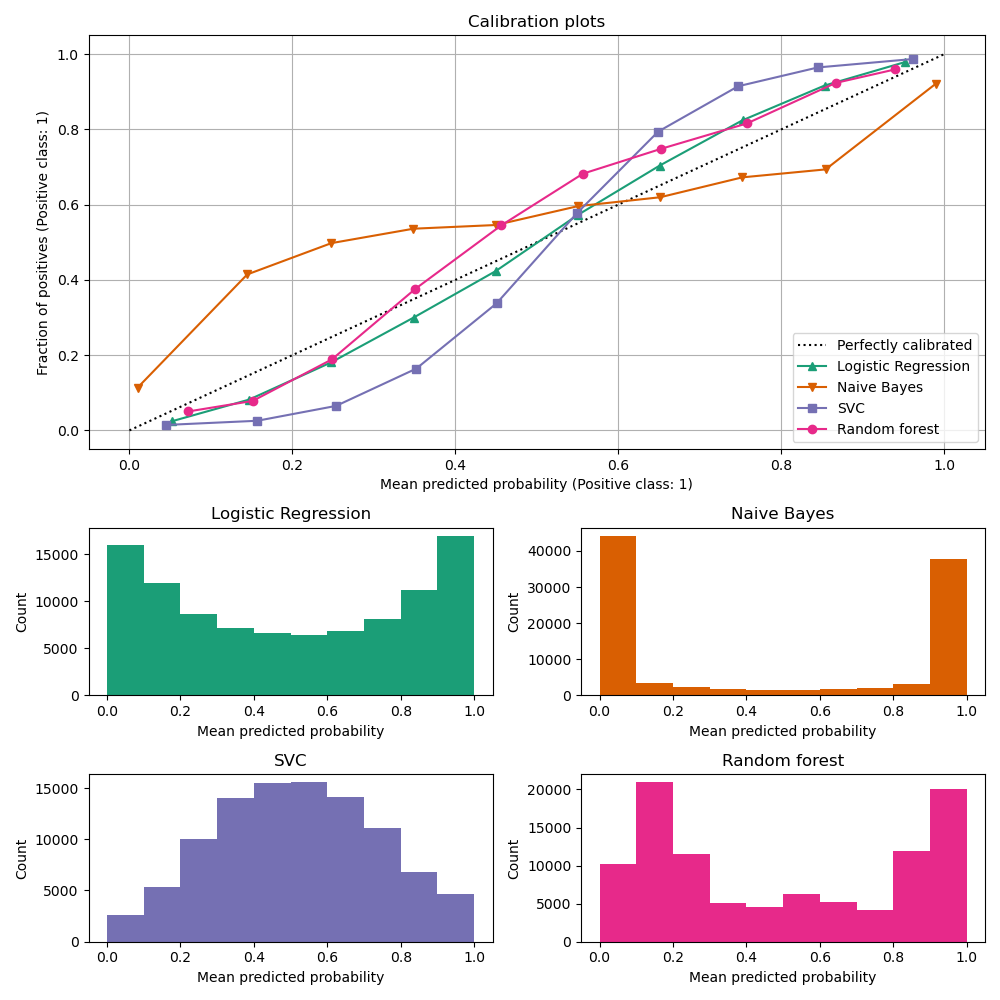
LogisticRegression более вероятно возвращает хорошо калиброванные предсказания сам по себе, поскольку имеет каноническую функцию связи для своей функции потерь, т.е. логит-связь для Логарифмическая потеря.
В случае без штрафа это приводит к так называемому свойство баланса, см. [8] и Логистическая регрессия.
На графике выше данные генерируются в соответствии с линейным механизмом, что
согласуется с LogisticRegression модель (модель 'корректно специфицирована'),
и значение параметра регуляризации C настроен так, чтобы быть подходящим (не слишком сильным и не слишком слабым). Как следствие, эта модель возвращает точные прогнозы с самого predict_proba метод.
В отличие от этого, другие показанные модели возвращают смещённые вероятности; с
разными смещениями для каждой модели.
GaussianNB (Наивный Байес) стремится подтолкнуть вероятности к 0 или 1 (обратите внимание на подсчеты
в гистограммах). Это в основном потому, что он делает предположение, что
признаки условно независимы при заданном классе, что не
так в этом наборе данных, который содержит 2 избыточных признака.
RandomForestClassifier показывает противоположное поведение: гистограммы
показывают пики при вероятностях примерно 0.2 и 0.9, в то время как вероятности
близкие к 0 или 1 очень редки. Объяснение этому дано
Niculescu-Mizil и Caruana [3]: «Методы, такие как бэггинг и случайные леса, которые усредняют предсказания из базового набора моделей, могут иметь трудности с предсказаниями около 0 и 1, потому что дисперсия в базовых моделях будет смещать предсказания, которые должны быть около нуля или единицы, от этих значений. Поскольку предсказания ограничены интервалом [0,1], ошибки, вызванные дисперсией, имеют тенденцию быть односторонними около нуля и единицы. Например, если модель должна предсказать \(p = 0\) для случая, единственный способ, которым бэггинг может достичь этого, — если все деревья в бэггинге предсказывают ноль. Если мы добавим шум к деревьям, которые усредняет бэггинг, этот шум заставит некоторые деревья предсказывать значения больше 0 для этого случая, тем самым отодвигая среднее предсказание ансамбля бэггинга от 0. Мы наблюдаем этот эффект наиболее сильно в случайных лесах, потому что базовые деревья, обученные с помощью случайных лесов, имеют относительно высокую дисперсию из-за подвыборки признаков.” В результате калибровочная кривая показывает характерную сигмоидальную форму, указывая, что классификатор мог бы больше доверять своей “интуиции” и возвращать вероятности, обычно ближе к 0 или 1.
LinearSVC (SVC) показывает еще более сигмоидальную кривую, чем случайный лес, что типично для методов максимального запаса (сравните Niculescu-Mizil и Caruana [3]), которые фокусируются на трудных для классификации образцах, которые находятся близко к границе решения (опорные векторы).
1.16.2. Калибровка классификатора#
Калибровка классификатора включает подгонку регрессора (называемого калибратор), который отображает выход классификатора (как задано decision_function или predict_proba) в калиброванную вероятность в [0, 1]. Обозначая выход классификатора для данного образца как \(f_i\), калибратор пытается предсказать условную вероятность события \(P(y_i = 1 | f_i)\).
В идеале калибратор настраивается на наборе данных, независимом от обучающих данных, использованных для первоначальной настройки классификатора. Это связано с тем, что производительность классификатора на его обучающих данных будет лучше, чем на новых данных. Использование вывода классификатора на обучающих данных для настройки калибратора привело бы к смещенному калибратору, который отображает вероятности ближе к 0 и 1, чем должно быть.
1.16.3. Использование#
The CalibratedClassifierCV класс используется для калибровки классификатора.
CalibratedClassifierCV использует подход кросс-валидации, чтобы гарантировать, что для обучения калибратора всегда используются несмещенные данные. Данные разделяются на \(k\)
(train_set, test_set) пары (как определено cv). Когда ensemble=True
(по умолчанию), следующая процедура повторяется независимо для каждого разбиения перекрёстной проверки:
клон
base_estimatorобучается на обучающем подмножествеобученный
base_estimatorделает предсказания на тестовом подмножествепрогнозы используются для обучения калибратора (сигмоидального или изотонического регрессора) (в случае многоклассовых данных калибратор обучается для каждого класса)
Это приводит к ансамблю из \(k\) (classifier, calibrator) пары, где каждый калибратор преобразует выход своего соответствующего классификатора в [0, 1]. Каждая пара представлена в calibrated_classifiers_ атрибут, где каждая запись представляет собой калиброванный классификатор с predict_proba метод, который выдает калиброванные вероятности. Выходные данные predict_proba для основного
CalibratedClassifierCV экземпляр соответствует среднему значению прогнозируемых вероятностей \(k\) оценщики в calibrated_classifiers_
список. Выходные данные predict — это класс, который имеет наивысшую вероятность.
Важно выбрать cv осторожно при использовании ensemble=True.
Все классы должны присутствовать как в обучающем, так и в тестовом подмножествах для каждого разбиения.
Когда класс отсутствует в обучающем подмножестве, прогнозируемая вероятность для этого
класса по умолчанию будет равна 0 для (classifier, calibrator) пары этого разделения. Это искажает predict_proba поскольку усредняет по всем парам. Когда класс отсутствует в тестовом подмножестве, калибратор для этого класса (внутри (classifier, calibrator) пара (этого разбиения) обучается на данных без положительного класса. Это приводит к неэффективной калибровке.
Когда ensemble=False, перекрестная проверка используется для получения 'несмещенных' прогнозов для всех данных через
cross_val_predict. Эти несмещенные прогнозы затем используются для обучения калибратора. Атрибут
calibrated_classifiers_ состоит только из одного (classifier, calibrator)
пара, где классификатор является base_estimator обучен на всех данных.
В этом случае выход predict_proba для
CalibratedClassifierCV это предсказанные вероятности, полученные
из одного (classifier, calibrator) пара.
Основное преимущество ensemble=True заключается в получении преимущества от традиционного эффекта ансамблирования (аналогично Мета-оценщик бэггинга). Полученный ансамбль должен
быть как хорошо калиброванным, так и немного более точным, чем с ensemble=False.
Основное преимущество использования ensemble=False вычислительный: он сокращает общее время обучения, обучая только одну пару базового классификатора и калибратора, уменьшает итоговый размер модели и увеличивает скорость предсказания.
В качестве альтернативы уже обученный классификатор может быть откалиброван с использованием
FrozenEstimator как
CalibratedClassifierCV(estimator=FrozenEstimator(estimator)). Пользователь должен убедиться, что данные, используемые для обучения классификатора, не пересекаются с данными, используемыми для обучения регрессора.
CalibratedClassifierCV поддерживает использование двух методов регрессии
для калибровки через method параметр: "sigmoid" и "isotonic".
1.16.3.1. Сигмоида#
Сигмоидный регрессор, method="sigmoid" основан на логистической модели Платта [4]:
где \(y_i\) это истинная метка образца \(i\) и \(f_i\) является выводом некалиброванного классификатора для выборки \(i\). \(A\) и \(B\) являются вещественными числами, которые определяются при обучении регрессора с помощью метода максимального правдоподобия.
Сигмоидный метод предполагает, что кривая калибровки может быть исправлено применением сигмоидной функции к сырым предсказаниям. Это предположение было эмпирически обосновано в случае Метод опорных векторов с общими функциями ядра на различных тестовых наборах данных в разделе 2.1 работы Platt 1999 [4] но не обязательно выполняется в общем случае. Кроме того, логистическая модель работает лучше всего, если ошибка калибровки симметрична, то есть выход классификатора для каждого бинарного класса нормально распределен с одинаковой дисперсией [7]. Это может быть проблемой для сильно несбалансированных задач классификации, где выходы не имеют равной дисперсии.
В целом этот метод наиболее эффективен для небольших размеров выборки или когда неквалиброванная модель недостаточно уверена и имеет схожие ошибки калибровки как для высоких, так и для низких выходных значений.
1.16.3.2. Изотоническая#
The method="isotonic" подгоняет непараметрический изотонический регрессор, который выводит ступенчатую неубывающую функцию, см. sklearn.isotonic. Минимизирует:
при условии \(\hat{f}_i \geq \hat{f}_j\) всякий раз, когда
\(f_i \geq f_j\). \(y_i\) является истинной
меткой образца \(i\) и \(\hat{f}_i\) является выходом
калиброванного классификатора для образца \(i\) (т.е. калиброванная вероятность).
Этот метод более универсален по сравнению с 'sigmoid' как единственное ограничение
состоит в том, что функция отображения монотонно возрастает. Таким образом, он более
мощен, так как может исправить любое монотонное искажение некалиброванной модели.
Однако он более склонен к переобучению, особенно на небольших наборах данных [6].
В целом, 'isotonic' будет работать так же хорошо или лучше, чем 'sigmoid' когда
достаточно данных (больше ~1000 выборок), чтобы избежать переобучения [3].
Примечание
Влияние на метрики ранжирования, такие как AUC
Обычно ожидается, что калибровка не влияет на ранжирующие метрики, такие как
ROC-AUC. Однако эти метрики могут отличаться после калибровки при использовании
method="isotonic" поскольку изотоническая регрессия вводит связи в предсказанных вероятностях. Это можно рассматривать как неопределенность предсказаний модели. В случае, если вы строго хотите сохранить ранжирование и, следовательно, оценки AUC, используйте
method="sigmoid" которая является строго монотонной трансформацией и, следовательно, сохраняет ранжирование.
1.16.3.3. Поддержка многоклассовой классификации#
Как изотонические, так и сигмоидные регрессоры поддерживают только одномерные данные (например, выход бинарной классификации), но расширены для многоклассовой классификации, если base_estimator поддерживает многоклассовые предсказания. Для многоклассовых предсказаний
CalibratedClassifierCV калибрует для каждого класса отдельно в OneVsRestClassifier мода [5]При предсказании вероятностей калиброванные вероятности для каждого класса предсказываются отдельно. Поскольку эти вероятности не обязательно суммируются в единицу, выполняется постобработка для их нормализации.
С другой стороны, температурное масштабирование естественным образом поддерживает многоклассовые прогнозы, работая с логитами и в конечном итоге применяя функцию softmax.
1.16.3.4. Температурное масштабирование#
Для задачи многоклассовой классификации с \(n\) классы, температурное масштабирование
[9], method="temperature"генерирует вероятности классов путем модификации функции softmax
с параметром температуры \(T\):
где, для данного образца, \(z\) является вектором логитов для каждого класса, предсказанных оценщиком, который нужно калибровать. В терминах API scikit-learn это соответствует выходу decision_function или к логарифму predict_proba. Вероятности преобразуются в логиты путем сначала добавления крошечной положительной константы, чтобы избежать числовых проблем с логарифмом нуля, а затем применения натурального логарифма.
Параметр \(T\) обучается путём минимизации log_loss,
т.е. потери перекрестной энтропии, на отложенном (калибровочном) наборе. Обратите внимание, что \(T\) не влияет на расположение максимума в выходе softmax. Поэтому температурное масштабирование не изменяет точность калибрующей оценки.
Основное преимущество температурного масштабирования перед другими методами калибровки заключается в том, что оно обеспечивает естественный способ получения (лучших) калиброванных вероятностей для многоклассовой классификации всего с одним свободным параметром, в отличие от использования схемы "Один против остальных", которая добавляет больше параметров для каждого отдельного класса.
Примеры
Ссылки