1.5. Стохастический градиентный спуск#

Стохастический градиентный спуск (SGD) является простым, но очень эффективным подходом к обучению линейных классификаторов и регрессоров с выпуклыми функциями потерь, такими как (линейная) Метод опорных векторов и Логистическая регрессияХотя SGD существует в сообществе машинного обучения уже давно, он получил значительное внимание лишь недавно в контексте обучения на больших данных.

SGD успешно применяется к крупномасштабным и разреженным задачам машинного обучения, часто встречающимся в классификации текста и обработке естественного языка. Учитывая, что данные разрежены, классификаторы в этом модуле легко масштабируются до задач с более чем \(10^5\) обучающих примеров и более чем \(10^5\) признаков.

Строго говоря, SGD — это всего лишь техника оптимизации и не соответствует конкретному семейству моделей машинного обучения. Это только способ для обучения модели. Часто экземпляр SGDClassifier или SGDRegressor будет иметь эквивалентный оценщик в API scikit-learn, потенциально использующий другую технику оптимизации. Например, используя SGDClassifier(loss='log_loss') приводит к логистической регрессии, т.е. модели, эквивалентной LogisticRegression который обучается с помощью SGD вместо обучения одним из других решателей в LogisticRegression. Аналогично, SGDRegressor(loss='squared_error', penalty='l2') и Ridge решают ту же задачу оптимизации, разными средствами.

Преимущества стохастического градиентного спуска:

  • Эффективность.

  • Простота реализации (много возможностей для настройки кода).

Недостатки стохастического градиентного спуска включают:

  • SGD требует ряда гиперпараметров, таких как параметр регуляризации и количество итераций.

  • SGD чувствителен к масштабированию признаков.

Предупреждение

Убедитесь, что вы переставляете (перемешиваете) ваши обучающие данные перед обучением модели или используйте shuffle=True перемешивать после каждой итерации (используется по умолчанию). Также, в идеале, признаки должны быть стандартизированы с помощью, например, make_pipeline(StandardScaler(), SGDClassifier()) (см. Конвейеры).

1.5.1. Классификация#

Класс SGDClassifier реализует простую процедуру обучения стохастического градиентного спуска, которая поддерживает различные функции потерь и штрафы для классификации. Ниже приведена граница решения SGDClassifier обучен с функцией потерь hinge, что эквивалентно линейному SVM.

../_images/sphx_glr_plot_sgd_separating_hyperplane_001.png

Как и другие классификаторы, SGD должен быть обучен с двумя массивами: массивом X формы (n_samples, n_features), содержащий обучающие выборки, и массив y формы (n_samples,) содержащий целевые значения (метки классов) для обучающих выборок:

>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = SGDClassifier(loss="hinge", penalty="l2", max_iter=5)
>>> clf.fit(X, y)
SGDClassifier(max_iter=5)

После обучения модель может использоваться для предсказания новых значений:

>>> clf.predict([[2., 2.]])
array([1])

SGD обучает линейную модель на обучающих данных. coef_ атрибут содержит параметры модели:

>>> clf.coef_
array([[9.9, 9.9]])

The intercept_ атрибут содержит свободный член (также называемый смещением или bias):

>>> clf.intercept_
array([-9.9])

Использовать ли модели перехват, т.е. смещенную гиперплоскость, контролируется параметром fit_intercept.

Знаковое расстояние до гиперплоскости (вычисленное как скалярное произведение между коэффициентами и входным образцом, плюс свободный член) задается формулой SGDClassifier.decision_function:

>>> clf.decision_function([[2., 2.]])
array([29.6])

Конкретная функция потерь может быть задана через loss параметр. SGDClassifier поддерживает следующие функции потерь:

  • loss="hinge": (мягкий зазор) линейная машина опорных векторов,

  • loss="modified_huber": сглаженная функция потерь hinge,

  • loss="log_loss": логистическая регрессия,

  • и все регрессионные потери ниже. В этом случае целевая переменная кодируется как \(-1\) или \(1\), и проблема рассматривается как проблема регрессии. Предсказанный класс тогда соответствует знаку предсказанной цели.

Пожалуйста, обратитесь к математический раздел ниже для формул. Первые две функции потерь являются ленивыми, они обновляют параметры модели только если пример нарушает ограничение по зазору, что делает обучение очень эффективным и может привести к более разреженным моделям (т.е. с большим количеством нулевых коэффициентов), даже когда \(L_2\) используется штраф.

Используя loss="log_loss" или loss="modified_huber" включает predict_proba метод, который дает вектор оценок вероятности \(P(y|x)\) на образец \(x\):

>>> clf = SGDClassifier(loss="log_loss", max_iter=5).fit(X, y)
>>> clf.predict_proba([[1., 1.]])
array([[0.00, 0.99]])

Конкретный штраф можно установить через penalty параметр. SGD поддерживает следующие штрафы:

  • penalty="l2": \(L_2\) нормальный штраф на coef_.

  • penalty="l1": \(L_1\) нормальный штраф на coef_.

  • penalty="elasticnet": Выпуклая комбинация \(L_2\) и \(L_1\); (1 - l1_ratio) * L2 + l1_ratio * L1.

Настройка по умолчанию — penalty="l2". \(L_1\) штраф приводит к разреженным решениям, обнуляя большинство коэффициентов. Elastic Net [11] решает некоторые недостатки \(L_1\) штраф в присутствии сильно коррелированных атрибутов. Параметр l1_ratio управляет выпуклой комбинацией \(L_1\) и \(L_2\) штраф.

SGDClassifier поддерживает многоклассовую классификацию путём объединения нескольких бинарных классификаторов в схему "один против всех" (OVA). Для каждого из \(K\) классов, обучается бинарный классификатор, который различает между этим и всеми остальными \(K-1\) классы. Во время тестирования мы вычисляем оценку уверенности (т.е., знаковые расстояния до гиперплоскости) для каждого классификатора и выбираем класс с наибольшей уверенностью. Рисунок ниже иллюстрирует подход OVA на наборе данных iris. Пунктирные линии представляют три классификатора OVA; фоновые цвета показывают поверхность решений, индуцированную тремя классификаторами.

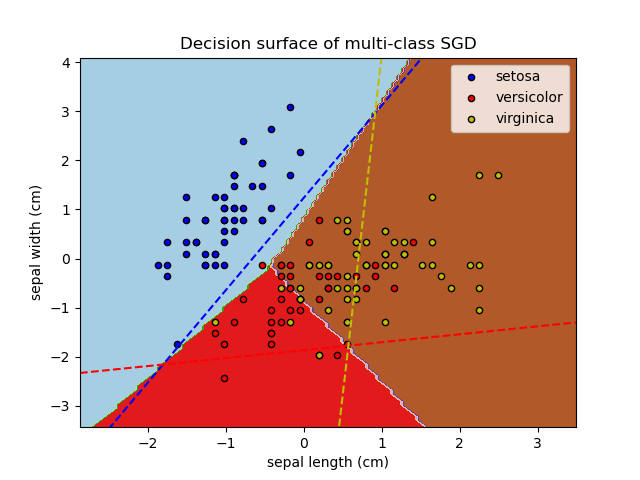
../_images/sphx_glr_plot_sgd_iris_001.png

В случае многоклассовой классификации coef_ является двумерным массивом формы (n_classes, n_features) и intercept_ является одномерным массивом формы (n_classes,). \(i\)-я строка coef_ содержит вектор весов классификатора OVA для \(i\)-го класса; классы индексируются в порядке возрастания (см. атрибут classes_). Обратите внимание, что в принципе, поскольку они позволяют создать вероятностную модель, loss="log_loss" и loss="modified_huber" более подходят для классификации "один против всех".

SGDClassifier поддерживает как взвешенные классы, так и взвешенные экземпляры через параметры fit class_weight и sample_weight. Смотрите примеры ниже и строку документации SGDClassifier.fit для дополнительной информации.

SGDClassifier поддерживает усредненный SGD (ASGD) [10]. Усреднение может быть включено путем установки average=True. ASGD выполняет те же обновления, что и обычный SGD (см. Математическая формулировка), но вместо использования последнего значения коэффициентов как coef_ атрибут (т.е. значения последнего обновления), coef_ установлен вместо среднее значение коэффициентов по всем обновлениям. То же самое делается для intercept_ атрибут. При использовании ASGD скорость обучения может быть выше и даже постоянной, что на некоторых наборах данных ускоряет время обучения.

Для классификации с логистической потерей доступен другой вариант SGD со стратегией усреднения с алгоритмом Stochastic Average Gradient (SAG), доступным как решатель в LogisticRegression.

Примеры

1.5.2. Регрессия#

Класс SGDRegressor реализует простую процедуру обучения стохастического градиентного спуска, которая поддерживает различные функции потерь и штрафы для подгонки линейных регрессионных моделей. SGDRegressor хорошо подходит для задач регрессии с большим количеством обучающих примеров (> 10.000), для других задач мы рекомендуем Ridge, Lasso, или ElasticNet.

Конкретная функция потерь может быть задана через loss параметр. SGDRegressor поддерживает следующие функции потерь:

  • loss="squared_error": Метод наименьших квадратов,

  • loss="huber": Потеря Хубера для робастной регрессии,

  • loss="epsilon_insensitive": линейная регрессия на основе метода опорных векторов.

Пожалуйста, обратитесь к математический раздел ниже для формул. Функции потерь Хубера и эпсилон-нечувствительные могут использоваться для робастной регрессии. Ширина нечувствительной области должна быть указана через параметр epsilon. Этот параметр зависит от масштаба целевых переменных.

The penalty параметр определяет используемую регуляризацию (см. описание выше в разделе классификации).

SGDRegressor также поддерживает усреднённый SGD [10] (здесь снова см. описание выше в разделе классификации).

Для регрессии с квадратичной потерей и \(L_2\) penalty, другой вариант SGD со стратегией усреднения доступен в алгоритме Stochastic Average Gradient (SAG), доступном как решатель в Ridge.

Примеры

1.5.3. Онлайн One-Class SVM#

Класс sklearn.linear_model.SGDOneClassSVM реализует онлайн-линейную версию One-Class SVM с использованием стохастического градиентного спуска. В сочетании с методами аппроксимации ядра, sklearn.linear_model.SGDOneClassSVM может использоваться для аппроксимации решения ядерного One-Class SVM, реализованного в sklearn.svm.OneClassSVM, с линейной сложностью по количеству выборок. Обратите внимание, что сложность ядерного One-Class SVM в лучшем случае квадратична по количеству выборок. sklearn.linear_model.SGDOneClassSVM поэтому хорошо подходит для наборов данных с большим количеством обучающих выборок (более 10 000), для которых SGD вариант может быть на несколько порядков быстрее.

Математические детали#

Его реализация основана на реализации стохастического градиентного спуска. Действительно, исходная задача оптимизации One-Class SVM задается как

\[\begin{split}\begin{aligned} \min_{w, \rho, \xi} & \quad \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \xi_i \\ \text{s.t.} & \quad \langle w, x_i \rangle \geq \rho - \xi_i \quad 1 \leq i \leq n \\ & \quad \xi_i \geq 0 \quad 1 \leq i \leq n \end{aligned}\end{split}\]

где \(\nu \in (0, 1]\) это пользовательский параметр, контролирующий долю выбросов и долю опорных векторов. Устранение переменных ослабления \(\xi_i\) эта задача эквивалентна

\[\min_{w, \rho} \frac{1}{2}\Vert w \Vert^2 - \rho + \frac{1}{\nu n} \sum_{i=1}^n \max(0, \rho - \langle w, x_i \rangle) \, .\]

Умножение на константу \(\nu\) и введение свободного члена \(b = 1 - \rho\) мы получаем следующую эквивалентную задачу оптимизации

\[\min_{w, b} \frac{\nu}{2}\Vert w \Vert^2 + b\nu + \frac{1}{n} \sum_{i=1}^n \max(0, 1 - (\langle w, x_i \rangle + b)) \, .\]

Это похоже на задачи оптимизации, изученные в разделе Математическая формулировка с \(y_i = 1, 1 \leq i \leq n\) и \(\alpha = \nu/2\), \(L\) является функцией потерь hinge, и \(R\) является \(L_2\) норма. Нам просто нужно добавить член \(b\nu\) в цикле оптимизации.

Поскольку SGDClassifier и SGDRegressor, SGDOneClassSVM поддерживает усредненный SGD. Усреднение можно включить, установив average=True.

Примеры

1.5.4. Стохастический градиентный спуск для разреженных данных#

Примечание

Разреженная реализация даёт слегка отличающиеся результаты от плотной реализации из-за уменьшенной скорости обучения для свободного члена. См. Детали реализации.

Встроенная поддержка разреженных данных, предоставленных в любой матрице в формате, поддерживаемом scipy.sparse. Для максимальной эффективности, однако, используйте формат CSR матрицы, как определено в scipy.sparse.csr_matrix.

Примеры

1.5.5. Сложность#

Основное преимущество SGD — его эффективность, которая в основном линейна по количеству обучающих примеров. Если \(X\) является матрицей размера \(n \times p\) (с \(n\) образцы и \(p\) признаков), обучение имеет стоимость \(O(k n \bar p)\), где \(k\) — это количество итераций (эпох), а \(\bar p\) является средним количеством ненулевых атрибутов на выборку.

Однако недавние теоретические результаты показывают, что время выполнения для достижения желаемой точности оптимизации не увеличивается с ростом размера обучающей выборки.

1.5.6. Критерий остановки#

Классы SGDClassifier и SGDRegressor предоставляют два критерия для остановки алгоритма при достижении заданного уровня сходимости:

  • С early_stopping=True, входные данные разделяются на обучающий набор и проверочный набор. Затем модель обучается на обучающем наборе, а критерий остановки основан на прогнозной оценке (с использованием score метода), вычисленного на валидационном наборе. Размер валидационного набора можно изменить с помощью параметра validation_fraction.

  • С early_stopping=False, модель обучается на всех входных данных, а критерий остановки основан на целевой функции, вычисленной на обучающих данных.

В обоих случаях критерий оценивается один раз за эпоху, и алгоритм останавливается, когда критерий не улучшается n_iter_no_change gcv_mode: {'auto', 'svd', 'eigen'}, по умолчанию='auto' tol, и алгоритм останавливается в любом случае после максимального числа итераций max_iter.

См. Ранняя остановка стохастического градиентного спуска для примера эффектов ранней остановки.

1.5.7. Советы по практическому использованию#

  • Стохастический градиентный спуск чувствителен к масштабированию признаков, поэтому настоятельно рекомендуется масштабировать данные. Например, масштабируйте каждый атрибут входного вектора \(X\) to \([0,1]\) или \([-1,1]\), или стандартизировать её, чтобы иметь среднее \(0\) и дисперсия \(1\). Обратите внимание, что тот же масштабирование должно быть применено к тестовому вектору для получения значимых результатов. Это можно легко сделать с помощью StandardScaler:

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)  # Don't cheat - fit only on training data
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)  # apply same transformation to test data

# Or better yet: use a pipeline!
from sklearn.pipeline import make_pipeline
est = make_pipeline(StandardScaler(), SGDClassifier())
est.fit(X_train)
est.predict(X_test)

    Если ваши атрибуты имеют внутренний масштаб (например, частоты слов или индикаторные признаки), масштабирование не требуется.

  • Нахождение разумного регуляризационного члена \(\alpha\) лучше всего выполнять с помощью автоматического поиска гиперпараметров, например, GridSearchCV или RandomizedSearchCV, обычно в диапазоне 10.0**-np.arange(1,7).

  • Эмпирически мы обнаружили, что SGD сходится после наблюдения примерно \(10^6\) обучающих образцов. Таким образом, разумное первоначальное предположение для количества итераций — max_iter = np.ceil(10**6 / n), где n это размер обучающей выборки.

  • Если вы применяете SGD к признакам, извлеченным с помощью PCA, мы обнаружили, что часто целесообразно масштабировать значения признаков на некоторую константу c таким образом, что среднее \(L_2\) норма обучающих данных равна единице.

  • Мы обнаружили, что усредненный SGD лучше всего работает с большим количеством признаков и более высоким eta0.

Ссылки

1.5.8. Математическая формулировка#

Мы описываем здесь математические детали процедуры SGD. Хороший обзор со скоростями сходимости можно найти в [12].

Для заданного набора обучающих примеров \(\{(x_1, y_1), \ldots, (x_n, y_n)\}\) где \(x_i \in \mathbf{R}^m\) и \(y_i \in \mathbf{R}\) (\(y_i \in \{-1, 1\}\) для классификации), наша цель — изучить линейную функцию оценки \(f(x) = w^T x + b\) с параметрами модели \(w \in \mathbf{R}^m\) и смещение \(b \in \mathbf{R}\). Для выполнения прогнозов в бинарной классификации мы просто смотрим на знак \(f(x)\)Чтобы найти параметры модели, мы минимизируем регуляризованную ошибку обучения, заданную выражением

\[E(w,b) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i)) + \alpha R(w)\]

где \(L\) является функцией потерь, которая измеряет (не)соответствие модели, и \(R\) является регуляризационным членом (также штрафом), который наказывает сложность модели; \(\alpha > 0\) является неотрицательным гиперпараметром, который контролирует силу регуляризации.

Подробности о функциях потерь#

Различные варианты для \(L\) подразумевают различные классификаторы или регрессоры:

  • Шарнирная (мягкая граница): эквивалентно классификации методом опорных векторов. \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))\).

  • Перцептрон: \(L(y_i, f(x_i)) = \max(0, - y_i f(x_i))\).

  • Модифицированный Хьюбер: \(L(y_i, f(x_i)) = \max(0, 1 - y_i f(x_i))^2\) if \(y_i f(x_i) > -1\), и \(L(y_i, f(x_i)) = -4 y_i f(x_i)\) в противном случае.

  • Логарифмическая потеря: эквивалентна логистической регрессии. \(L(y_i, f(x_i)) = \log(1 + \exp (-y_i f(x_i)))\).

  • Квадратичная ошибка: Линейная регрессия (Ridge или Lasso в зависимости от \(R\)). \(L(y_i, f(x_i)) = \frac{1}{2}(y_i - f(x_i))^2\).

  • Huber: менее чувствителен к выбросам, чем метод наименьших квадратов. Эквивалентен методу наименьших квадратов, когда \(|y_i - f(x_i)| \leq \varepsilon\), и \(L(y_i, f(x_i)) = \varepsilon |y_i - f(x_i)| - \frac{1}{2} \varepsilon^2\) в противном случае.

  • Эпсилон-нечувствительная: (мягкий зазор) эквивалентна регрессии опорных векторов. \(L(y_i, f(x_i)) = \max(0, |y_i - f(x_i)| - \varepsilon)\).

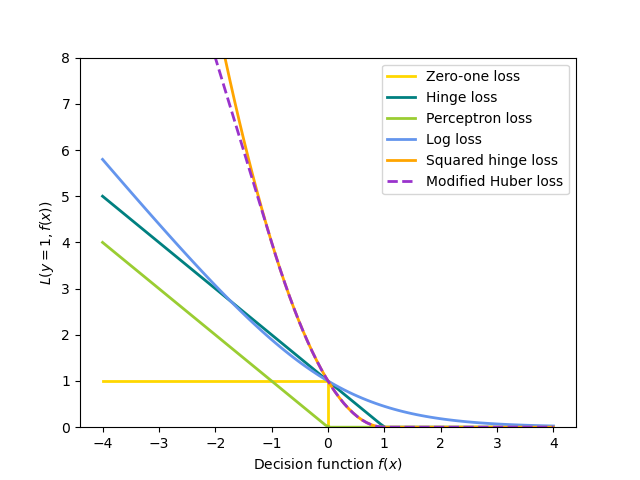
Все вышеперечисленные функции потерь можно рассматривать как верхнюю границу ошибки классификации (потеря 0-1), как показано на рисунке ниже.

../_images/sphx_glr_plot_sgd_loss_functions_001.png

Популярные варианты для регуляризационного члена \(R\) (the penalty параметр) включают:

  • \(L_2\) норма: \(R(w) := \frac{1}{2} \sum_{j=1}^{m} w_j^2 = ||w||_2^2\),

  • \(L_1\) норма: \(R(w) := \sum_{j=1}^{m} |w_j|\), что приводит к разреженным решениям.

  • Эластичная сеть: \(R(w) := \frac{\rho}{2} \sum_{j=1}^{n} w_j^2 + (1-\rho) \sum_{j=1}^{m} |w_j|\), выпуклая комбинация \(L_2\) и \(L_1\), где \(\rho\) задается формулой 1 - l1_ratio.

На рисунке ниже показаны контуры различных регуляризационных членов в двумерном пространстве параметров (\(m=2\)) когда \(R(w) = 1\).

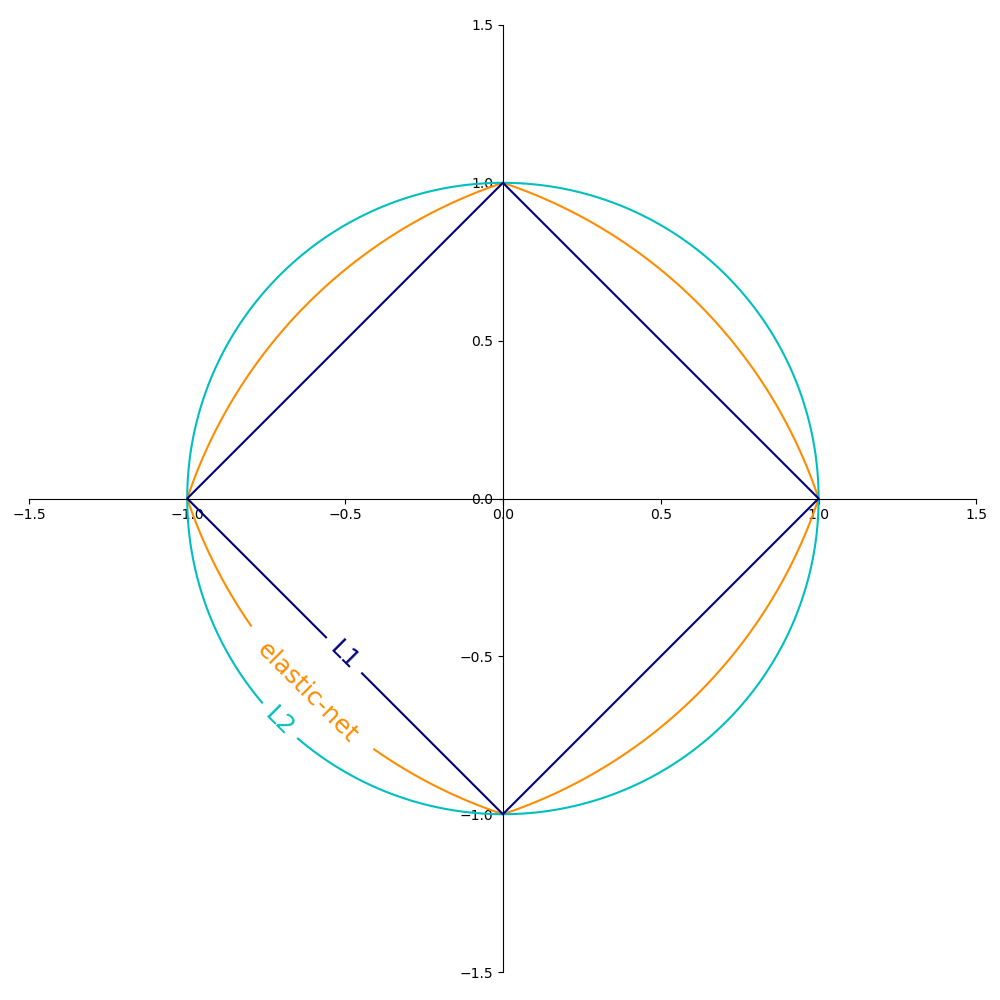
../_images/sphx_glr_plot_sgd_penalties_001.png

1.5.8.1. SGD#

Стохастический градиентный спуск — это метод оптимизации для неограниченных задач оптимизации. В отличие от (пакетного) градиентного спуска, SGD аппроксимирует истинный градиент \(E(w,b)\) рассматривая один обучающий пример за раз.

Класс SGDClassifier реализует процедуру обучения SGD первого порядка. Алгоритм итерируется по обучающим примерам и для каждого примера обновляет параметры модели в соответствии с правилом обновления, заданным

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial L(w^T x_i + b, y_i)}{\partial w}\right]\]

где \(\eta\) — это скорость обучения, которая контролирует размер шага в пространстве параметров. Свободный член \(b\) обновляется аналогично, но без регуляризации (и с дополнительным затуханием для разреженных матриц, как подробно описано в Детали реализации).

Скорость обучения \(\eta\) может быть либо постоянной, либо постепенно затухающей. Для классификации расписание скорости обучения по умолчанию (learning_rate='optimal') задается

\[\eta^{(t)} = \frac {1}{\alpha (t_0 + t)}\]

где \(t\) это временной шаг (всего есть n_samples * n_iter временные шаги), \(t_0\) определяется на основе эвристики, предложенной Леоном Ботту, таким образом, что ожидаемые начальные обновления сопоставимы с ожидаемым размером весов (это предполагает, что норма обучающих выборок приблизительно равна 1). Точное определение можно найти в _init_t в BaseSGD.

Для регрессии график скорости обучения по умолчанию — обратное масштабирование (learning_rate='invscaling'), заданный

\[\eta^{(t)} = \frac{\eta_0}{t^{power\_t}}\]

где \(\eta_0\) и \(power\_t\) являются гиперпараметрами, выбранными пользователем через eta0 и power_t, соответственно.

Для постоянной скорости обучения используйте learning_rate='constant' и использовать eta0 для указания скорости обучения.

Для адаптивно уменьшающейся скорости обучения используйте learning_rate='adaptive' и использовать eta0 для указания начальной скорости обучения. Когда достигается критерий остановки, скорость обучения делится на 5, и алгоритм не останавливается. Алгоритм останавливается, когда скорость обучения опускается ниже 1e-6.

Параметры модели доступны через coef_ и intercept_ атрибуты: coef_ содержит веса \(w\) и intercept_ содержит \(b\).

При использовании усреднённого SGD (с average параметр), coef_ устанавливается в средний вес по всем обновлениям: coef_ \(= \frac{1}{T} \sum_{t=0}^{T-1} w^{(t)}\), где \(T\) это общее количество обновлений, найденное в t_ атрибут.

1.5.9. Детали реализации#

Реализация SGD находится под влиянием Stochastic Gradient SVM of [7]. Аналогично SvmSGD, вектор весов представлен как произведение скаляра и вектора, что позволяет эффективное обновление весов в случае \(L_2\) регуляризация. В случае разреженного ввода X, перехват обновляется с меньшей скоростью обучения (умноженной на 0.01), чтобы учесть тот факт, что он обновляется чаще. Обучающие примеры выбираются последовательно, и скорость обучения снижается после каждого наблюдаемого примера. Мы приняли расписание скорости обучения из [8]. Для многоклассовой классификации используется подход 'один против всех'. Мы используем алгоритм усеченного градиента, предложенный в [9] для \(L_1\) регуляризация (и Elastic Net). Код написан на Cython.

Ссылки