7.6. Случайная проекция#
The sklearn.random_projection модуль реализует простой и вычислительно эффективный способ уменьшения размерности данных путём обмена контролируемого количества точности (как дополнительной дисперсии) на более быструю обработку и меньшие размеры моделей. Этот модуль реализует два типа неструктурированных случайных матриц:
Гауссова случайная матрица и
разреженная случайная матрица.
тестирование, документация, примеры, тесты
Ссылки
Санджой Дасгупта. 2000. Эксперименты со случайным проецированием. В материалах Шестнадцатой конференции по неопределенности в искусственном интеллекте (UAI’00), под ред. Крейга Боутильера и Моисеса Голдсмита. Morgan Kaufmann Publishers Inc., Сан-Франциско, Калифорния, США, 143-151.
Элла Бингем и Хейкки Маннила. 2001. Случайное проецирование в снижении размерности: применение к изображениям и текстовым данным. В материалах седьмой международной конференции ACM SIGKDD по обнаружению знаний и анализу данных (KDD '01). ACM, Нью-Йорк, Нью-Йорк, США, 245-250.
7.6.1. Лемма Джонсона-Линденштраусса#
Основной теоретический результат, лежащий в основе эффективности случайного проецирования, это Лемма Джонсона-Линденштраусса (цитата из Википедии):
В математике лемма Джонсона-Линденштраусса — это результат, касающийся вложений точек из высокоразмерного пространства в низкоразмерное евклидово пространство с малыми искажениями. Лемма утверждает, что небольшой набор точек в высокоразмерном пространстве может быть вложен в пространство гораздо меньшей размерности таким образом, что расстояния между точками почти сохраняются. Отображение, используемое для вложения, является по крайней мере липшицевым и может быть даже взято как ортогональная проекция.
Зная только количество образцов,
johnson_lindenstrauss_min_dim консервативно оценивает минимальный размер случайного подпространства для гарантии ограниченного искажения, вносимого случайной проекцией:
>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
np.int64(663)
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([ 663, 11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894, 9868, 11841])
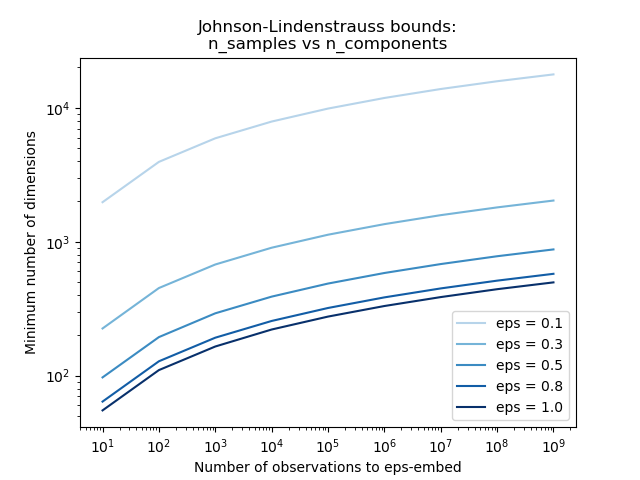
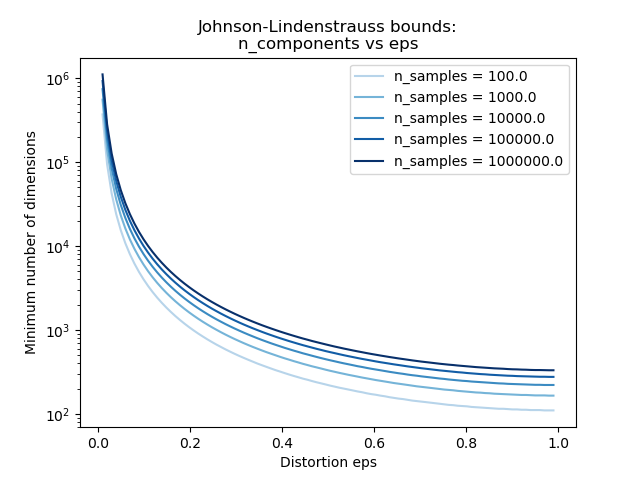
Примеры
См. Граница Джонсона-Линденштрауса для вложения с помощью случайных проекций для теоретического объяснения леммы Джонсона-Линденштраусса и эмпирической проверки с использованием разреженных случайных матриц.
Ссылки
Sanjoy Dasgupta и Anupam Gupta, 1999. Элементарное доказательство леммы Джонсона-Линденштраусса.
7.6.2. Гауссово случайное проецирование#
The GaussianRandomProjection уменьшает размерность, проецируя исходное входное пространство на случайно сгенерированную матрицу, где компоненты взяты из следующего распределения
\(N(0, \frac{1}{n_{components}})\).
Вот небольшой отрывок, иллюстрирующий использование преобразователя Гауссовского случайного проецирования:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
7.6.3. Разреженная случайная проекция#
The SparseRandomProjection уменьшает
размерность, проецируя исходное входное пространство с использованием разреженной
случайной матрицы.
Разреженные случайные матрицы являются альтернативой плотным гауссовым случайным матрицам проекции, которые гарантируют аналогичное качество вложения при значительно большей эффективности использования памяти и позволяют быстрее вычислять спроецированные данные.
Если мы определим s = 1 / density, элементы случайной матрицы
извлекаются из
где \(n_{\text{components}}\) — это размер проецируемого подпространства. По умолчанию плотность ненулевых элементов установлена на минимальную плотность, как рекомендовано Ping Li и др.: \(1 / \sqrt{n_{\text{features}}}\).
Вот небольшой отрывок, иллюстрирующий использование разреженного проекционного преобразователя со случайными значениями:
>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
Ссылки
D. Achlioptas. 2003. Дружественные к базам данных случайные проекции: Джонсон-Линденштраусс с бинарными монетами. Journal of Computer and System Sciences 66 (2003) 671-687.
Пинг Ли, Тревор Дж. Хасти и Кеннет В. Черч. 2006. Очень разреженные случайные проекции. В материалах 12-й международной конференции ACM SIGKDD по обнаружению знаний и анализу данных (KDD '06). ACM, Нью-Йорк, Нью-Йорк, США, 287-296.
7.6.4. Обратное преобразование#
Преобразователи случайного проецирования имеют compute_inverse_components параметр. Когда установлено значение True, после создания случайного components_ матрицу во время обучения,
преобразователь вычисляет псевдообратную этой матрицы и сохраняет её как
inverse_components_. inverse_components_ матрица имеет форму
\(n_{features} \times n_{components}\), и это всегда плотная матрица,
независимо от того, является ли матрица компонентов разреженной или плотной. Поэтому в зависимости от
количества признаков и компонентов, она может использовать много памяти.
Когда inverse_transform при вызове метода вычисляется произведение входных данных X и транспонированием обратных компонентов. Если обратные компоненты были
вычислены во время обучения, они повторно используются при каждом вызове inverse_transform. В противном случае они пересчитываются каждый раз, что может быть затратно. Результат всегда плотный, даже если X является разреженной.
Вот небольшой пример кода, который иллюстрирует, как использовать обратное преобразование признаков:
>>> import numpy as np
>>> from sklearn.random_projection import SparseRandomProjection
>>> X = np.random.rand(100, 10000)
>>> transformer = SparseRandomProjection(
... compute_inverse_components=True
... )
...
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
>>> X_new_inversed = transformer.inverse_transform(X_new)
>>> X_new_inversed.shape
(100, 10000)
>>> X_new_again = transformer.transform(X_new_inversed)
>>> np.allclose(X_new, X_new_again)
True