1.7. Гауссовские процессы

Гауссовские процессы (GP) являются непараметрическим методом обучения с учителем, используемым для решения регрессия и вероятностная классификация задачи.

Преимущества гауссовских процессов:

• Предсказание интерполирует наблюдения (по крайней мере, для регулярных ядер).

• Прогноз является вероятностным (гауссовским), поэтому можно вычислить эмпирические доверительные интервалы и решить на их основе, следует ли переобучать (онлайн-обучение, адаптивное обучение) прогноз в некоторой области интереса.

• Универсальный: различные kernels могут быть указаны. Предоставляются общие ядра, но также возможно указать пользовательские ядра.

Недостатки гауссовских процессов включают:

• Наша реализация не является разреженной, т.е. она использует всю информацию выборок/признаков для выполнения предсказания.

• Они теряют эффективность в пространствах высокой размерности — а именно, когда количество признаков превышает несколько десятков.

1.7.1. Гауссовская процессная регрессия (GPR)

The GaussianProcessRegressor реализует гауссовские процессы (GP) для целей регрессии. Для этого необходимо указать априорное распределение GP. GP объединит это априорное распределение и функцию правдоподобия на основе обучающих выборок. Это позволяет дать вероятностный подход к прогнозированию, предоставляя среднее значение и стандартное отклонение на выходе при предсказании.

Предполагается, что априорное среднее постоянно и равно нулю (для normalize_y=False) или среднее обучающих данных (для normalize_y=True). Ковариация априорного распределения задаётся передачей ядро объект. Гиперпараметры ядра оптимизируются при обучении GaussianProcessRegressor путем максимизации логарифма маргинального правдоподобия (LML) на основе переданных optimizer. Поскольку LML может иметь несколько локальных оптимумов, оптимизатор можно запускать многократно, указав n_restarts_optimizer. Первый запуск всегда проводится, начиная с начальных значений гиперпараметров ядра; последующие запуски проводятся из значений гиперпараметров, выбранных случайным образом из диапазона допустимых значений. Если начальные гиперпараметры должны оставаться фиксированными, None может быть передан как оптимизатор.

Уровень шума в целевых переменных может быть задан путем передачи его через параметр alpha, либо глобально как скаляр, либо для каждой точки данных. Обратите внимание, что умеренный уровень шума также может быть полезен для работы с числовой нестабильностью во время обучения, так как он эффективно реализуется как регуляризация Тихонова, т.е. путем добавления его к диагонали матрицы ядра. Альтернативой явному указанию уровня шума является включение WhiteKernel компонент в ядро, которое может оценить глобальный уровень шума по данным (см. 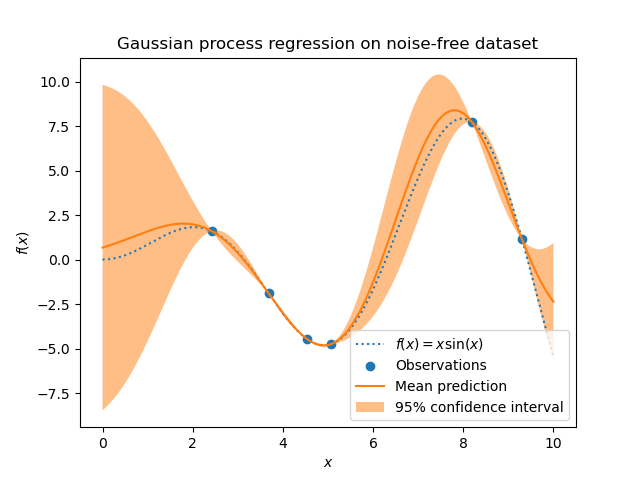пример ниже). На рисунке ниже показан эффект обработки зашумленной цели путем установки параметра alpha.

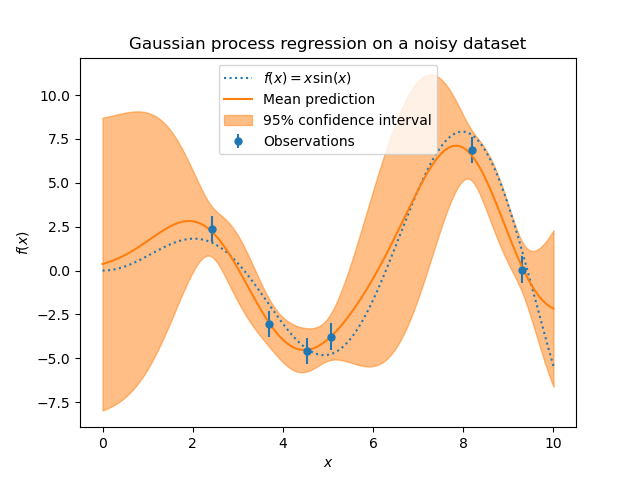
Реализация основана на алгоритме 2.1 из [RW2006]. В дополнение к API стандартных оценщиков scikit-learn, GaussianProcessRegressor:

• позволяет предсказывать без предварительной подгонки (на основе априорного GP)

• предоставляет дополнительный метод sample_y(X), которая оценивает выборки, полученные из GPR (априорного или апостериорного), при заданных входных данных

• предоставляет метод log_marginal_likelihood(theta), которые могут использоваться внешне для других способов выбора гиперпараметров, например, через метод Монте-Карло по цепи Маркова.

Примеры

• Регрессия гауссовских процессов: базовый вводный пример

• Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных

• Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов

• Прогнозирование уровня CO2 на наборе данных Mona Loa с использованием гауссовской регрессии (GPR)

1.7.2. Гауссовский процесс классификации (GPC)

The GaussianProcessClassifier реализует гауссовские процессы (GP) для целей классификации, более конкретно для вероятностной классификации, где тестовые предсказания принимают форму вероятностей классов. GaussianProcessClassifier помещает априорное распределение GP на скрытую функцию \(f\), который затем преобразуется через функцию связи \(\pi\) для получения вероятностной классификации. Скрытая функция \(f\) является так называемой мешающей функцией, чьи значения не наблюдаются и сами по себе не важны. Её цель — обеспечить удобную формулировку модели, и \(f\) удаляется (интегрируется) во время предсказания. GaussianProcessClassifier реализует логистическую функцию связи, для которой интеграл не может быть вычислен аналитически, но легко аппроксимируется в бинарном случае.

В отличие от регрессионной настройки, апостериорная скрытой функции \(f\) не является гауссовским даже для априорного GP, поскольку гауссовское правдоподобие неприменимо для дискретных меток классов. Вместо этого используется негауссовское правдоподобие, соответствующее логит-функции связи. GaussianProcessClassifier аппроксимирует негауссовский апостериорный с гауссовским на основе аппроксимации Лапласа. Подробнее можно найти в главе 3 [RW2006].

Среднее априорного распределения гауссовского процесса предполагается равным нулю. Ковариация априорного распределения задаётся передачей ядро объекта. Гиперпараметры ядра оптимизируются в процессе обучения GaussianProcessRegressor путем максимизации логарифмической маргинальной вероятности (LML) на основе переданных optimizer. Поскольку LML может иметь несколько локальных оптимумов, оптимизатор можно запускать многократно, указывая n_restarts_optimizer. Первый запуск всегда проводится, начиная с начальных значений гиперпараметров ядра; последующие запуски проводятся со значений гиперпараметров, выбранных случайным образом из диапазона допустимых значений. Если начальные гиперпараметры должны оставаться фиксированными, None может быть передан как оптимизатор.

В некоторых сценариях информация о латентной функции \(f\) желательно (т.е. среднее \(\bar{f_*}\) и дисперсия \(\text{Var}[f_*]\) описанный в уравнениях (3.21) и (3.24) из [RW2006]). GaussianProcessClassifier предоставляет доступ к этим величинам через latent_mean_and_variance метод.

GaussianProcessClassifier поддерживает многоклассовую классификацию путем выполнения обучения и предсказания на основе стратегии «один против всех» или «один против одного». В стратегии «один против всех» для каждого класса обучается один бинарный классификатор Гауссовского процесса, который обучается отделять этот класс от остальных. В стратегии «one_vs_one» для каждой пары классов обучается один бинарный классификатор Гауссовского процесса, который обучается отделять эти два класса. Предсказания этих бинарных классификаторов объединяются в многоклассовые предсказания. См. раздел о многоклассовая классификация для получения дополнительной информации.

В случае классификации по гауссовским процессам, “one_vs_one” может быть вычислительно дешевле, поскольку он решает множество задач, включающих только подмножество всего обучающего набора, а не меньшее количество задач на всем наборе данных. Поскольку классификация по гауссовским процессам масштабируется кубически с размером набора данных, это может быть значительно быстрее. Однако обратите внимание, что “one_vs_one” не поддерживает предсказание оценок вероятности, а только простые предсказания. Более того, обратите внимание, что GaussianProcessClassifier не реализует (пока) истинное многоклассовое приближение Лапласа внутри, но, как обсуждалось выше, основан на решении нескольких задач бинарной классификации внутри, которые комбинируются с использованием one-versus-rest или one-versus-one.

1.7.3. Примеры GPC

1.7.3.1. Вероятностные предсказания с GPC

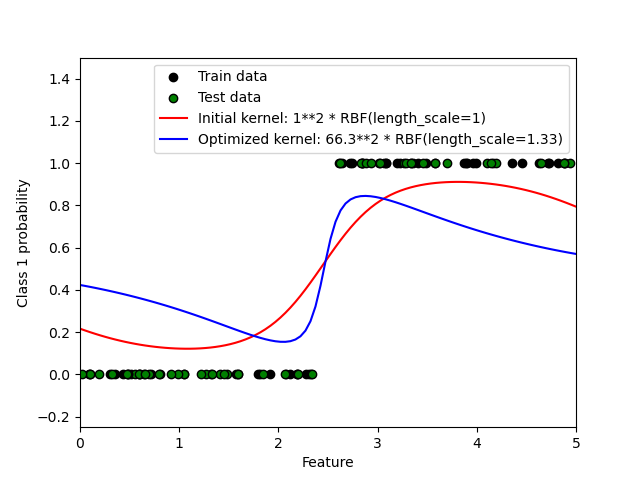
Этот пример иллюстрирует предсказанную вероятность GPC для RBF ядра с различными вариантами гиперпараметров. Первый рисунок показывает предсказанную вероятность GPC с произвольно выбранными гиперпараметрами и с гиперпараметрами, соответствующими максимальному логарифмическому маргинальному правдоподобию (LML).

Хотя гиперпараметры, выбранные путем оптимизации LML, имеют значительно большее значение LML, они работают немного хуже согласно логарифмическим потерям на тестовых данных. На рисунке показано, что это происходит потому, что они демонстрируют резкое изменение вероятностей классов на границах классов (что хорошо), но имеют предсказанные вероятности, близкие к 0.5, далеко от границ классов (что плохо). Этот нежелательный эффект вызван приближением Лапласа, используемым внутренне в GPC.

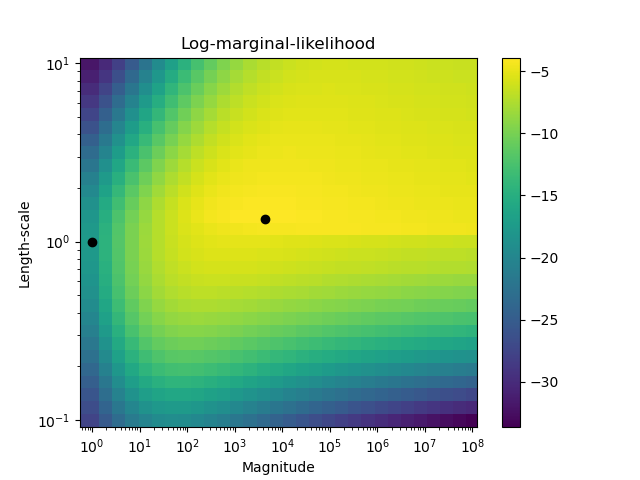
Второй рисунок показывает логарифмическую маргинальную вероятность для различных вариантов гиперпараметров ядра, выделяя два выбора гиперпараметров, использованных на первом рисунке, черными точками.

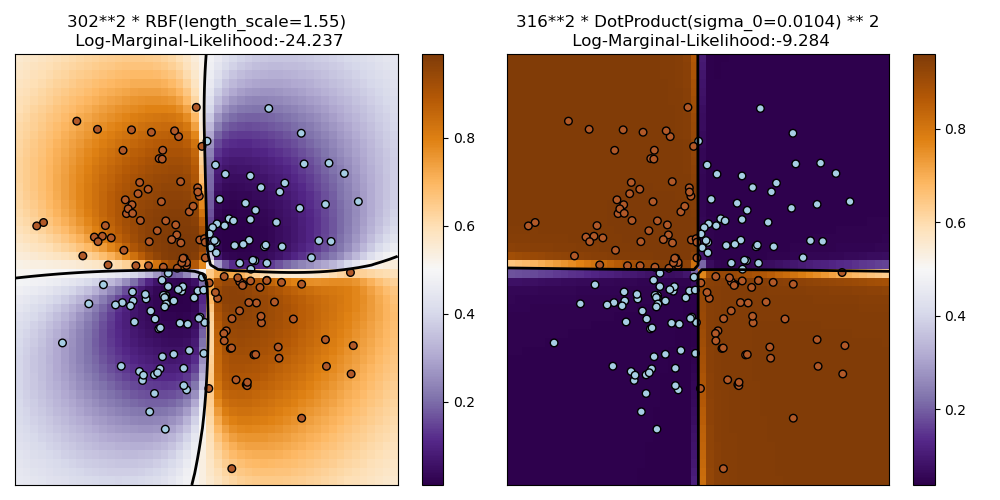
1.7.3.2. Иллюстрация GPC на наборе данных XOR

Этот пример иллюстрирует GPC на данных XOR. Сравниваются стационарное, изотропное ядро (RBF) и нестационарное ядро (DotProduct). На этом конкретном наборе данных, DotProduct ядро получает значительно лучшие результаты, потому что границы классов линейны и совпадают с координатными осями. Однако на практике стационарные ядра, такие как RBF часто дают лучшие результаты.

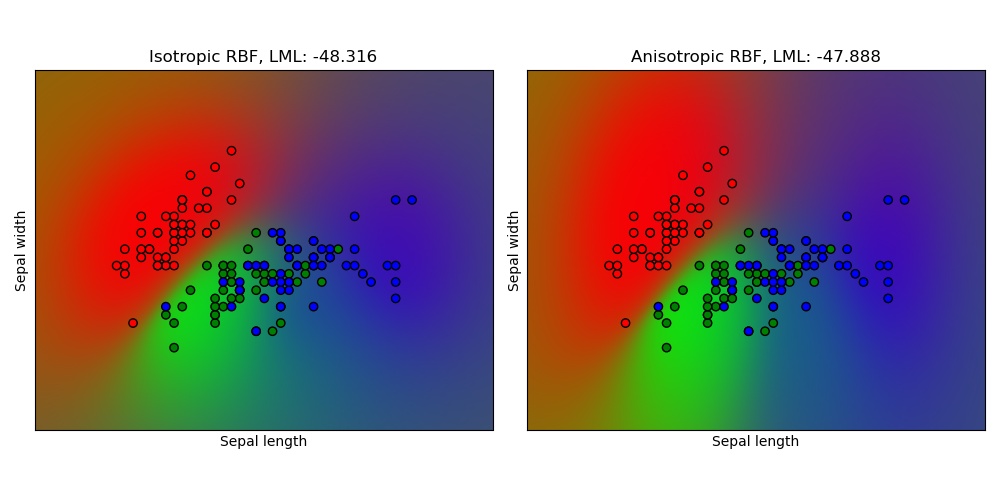
1.7.3.3. Гауссовский процесс классификации (GPC) на наборе данных iris

Этот пример иллюстрирует предсказанную вероятность GPC для изотропного и анизотропного RBF ядра на двумерной версии набора данных ириса. Это демонстрирует применимость GPC к небинарной классификации. Анизотропное RBF ядро получает немного более высокое логарифмическое маргинальное правдоподобие, назначая разные длины масштаба двум измерениям признаков.

1.7.4. Ядра для гауссовских процессов

Ядра (также называемые «ковариационными функциями» в контексте гауссовских процессов) являются ключевым компонентом ГП, который определяет форму априорного и апостериорного распределений ГП. Они кодируют предположения об изучаемой функции, определяя «сходство» двух точек данных в сочетании с предположением, что похожие точки данных должны иметь похожие целевые значения. Можно выделить две категории ядер: стационарные ядра зависят только от расстояния между двумя точками данных, а не от их абсолютных значений \(k(x_i, x_j)= k(d(x_i, x_j))\) и поэтому инвариантны к сдвигам во входном пространстве, в то время как нестационарные ядра также зависят от конкретных значений точек данных. Стационарные ядра можно дополнительно разделить на изотропные и анизотропные, где изотропные ядра также инвариантны к вращениям во входном пространстве. Для получения дополнительной информации см. главу 4 [RW2006]. Этот пример показывает, как определить пользовательское ядро для дискретных данных. Для рекомендаций по наилучшему сочетанию различных ядер мы отсылаем к [Duv2014].

API ядра гауссовского процесса

Основное использование Kernel заключается в вычислении ковариации гауссовского процесса между точками данных. Для этого метод __call__ ядра может быть вызван. Этот метод может использоваться для вычисления "автоковариации" всех пар точек данных в двумерном массиве X или "перекрестной ковариации" всех комбинаций точек данных двумерного массива X с точками данных в двумерном массиве Y. Следующее тождество верно для всех ядер k (кроме WhiteKernel): k(X) == K(X, Y=X)

Если используется только диагональ автоковариации, метод diag() ядра может быть вызван, что вычислительно эффективнее, чем эквивалентный вызов __call__: np.diag(k(X, X)) == k.diag(X)

Ядра параметризуются вектором \(\theta\) гиперпараметров. Эти гиперпараметры могут, например, управлять масштабами длины или периодичностью ядра (см. ниже). Все ядра поддерживают вычисление аналитических градиентов автоковариации ядра относительно \(log(\theta)\) через установку eval_gradient=True в __call__ метод. То есть, (len(X), len(X), len(theta)) возвращается массив, где элемент [i, j, l] содержит \(\frac{\partial k_\theta(x_i, x_j)}{\partial log(\theta_l)}\). Этот градиент используется гауссовским процессом (как регрессором, так и классификатором) при вычислении градиента логарифмической маргинальной вероятности, который, в свою очередь, используется для определения значения \(\theta\), который максимизирует логарифмическую маргинальную вероятность, с помощью градиентного подъёма. Для каждого гиперпараметра начальное значение и границы должны быть указаны при создании экземпляра ядра. Текущее значение \(\theta\) можно получить и установить через свойство theta объекта ядра. Кроме того, границы гиперпараметров могут быть доступны через свойство bounds ядра. Обратите внимание, что оба свойства (theta и bounds) возвращают логарифмически преобразованные значения внутренне используемых величин, поскольку они обычно более удобны для градиентной оптимизации. Спецификация каждого гиперпараметра хранится в виде экземпляра Hyperparameter в соответствующем ядре. Обратите внимание, что ядро, использующее гиперпараметр с именем "x", должно иметь атрибуты self.x и self.x_bounds.

Абстрактный базовый класс для всех ядер — это Kernel. Ядро реализует похожий интерфейс, как BaseEstimator, предоставляя методы get_params(), set_params(), и clone(). Это позволяет устанавливать значения ядра также через мета-оценщики, такие как Pipeline или GridSearchCV. Обратите внимание, что из-за вложенной структуры ядер (применением операторов ядер, см. ниже) имена параметров ядер могут стать относительно сложными. В общем случае для бинарного оператора ядра параметры левого операнда имеют префикс k1__ и параметры правого операнда с k2__. Дополнительный удобный метод — clone_with_theta(theta), который возвращает клонированную версию ядра, но с гиперпараметрами, установленными в theta. Наглядный пример:

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta)  # Note: log-transformed
[ 0.         -0.69314718  0.69314718]
>>> print(kernel.bounds)  # Note: log-transformed
[[      -inf 2.30258509]
[      -inf 2.30258509]
[      -inf 2.30258509]]

Все ядра гауссовских процессов совместимы с sklearn.metrics.pairwise и наоборот: экземпляры подклассов Kernel может быть передан как metric to pairwise_kernels из sklearn.metrics.pairwise. Кроме того, функции ядра из pairwise могут использоваться как ядра гауссовских процессов с помощью класса-обертки PairwiseKernel. Единственная оговорка заключается в том, что градиент гиперпараметров не аналитический, а численный, и все эти ядра поддерживают только изотропные расстояния. Параметр gamma считается гиперпараметром и может быть оптимизирован. Другие параметры ядра устанавливаются непосредственно при инициализации и остаются фиксированными.

1.7.4.1. Базовые ядра

The ConstantKernel ядро может использоваться как часть Product ядро, где оно масштабирует величину другого фактора (ядра) или как часть Sum ядро, где оно изменяет среднее гауссовского процесса. Зависит от параметра \(constant\_value\). Он определяется как:

\[k(x_i, x_j) = constant\_value \;\forall\; x_i, x_j\]

Основной вариант использования WhiteKernel ядро используется как часть суммарного ядра, где оно объясняет шумовую составляющую сигнала. Настройка его параметра \(noise\_level\) соответствует оценке уровня шума. Он определяется как:

\[k(x_i, x_j) = noise\_level \text{ if } x_i == x_j \text{ else } 0\]

1.7.4.2. Операторы ядра

Операторы ядра берут одно или два базовых ядра и комбинируют их в новое ядро. Sum ядро принимает два ядра \(k_1\) и \(k_2\) и объединяет их через \(k_{sum}(X, Y) = k_1(X, Y) + k_2(X, Y)\). Product ядро принимает два ядра \(k_1\) и \(k_2\) и объединяет их через \(k_{product}(X, Y) = k_1(X, Y) * k_2(X, Y)\). Exponentiation ядро принимает одно базовое ядро и скалярный параметр \(p\) и объединяет их через \(k_{exp}(X, Y) = k(X, Y)^p\). Обратите внимание, что магические методы __add__, __mul___ и __pow__ переопределяются на объектах Kernel, поэтому можно использовать, например, RBF() + RBF() как сокращение для Sum(RBF(), RBF()).

1.7.4.3. Радиальная базисная функция (RBF) ядро

The RBF ядро является стационарным ядром. Также известно как "квадратно-экспоненциальное" ядро. Параметризуется параметром масштаба длины \(l>0\), который может быть либо скаляром (изотропный вариант ядра), либо вектором с тем же количеством измерений, что и входные данные \(x\) (анизотропный вариант ядра). Ядро задается как:

\[k(x_i, x_j) = \text{exp}\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)\]

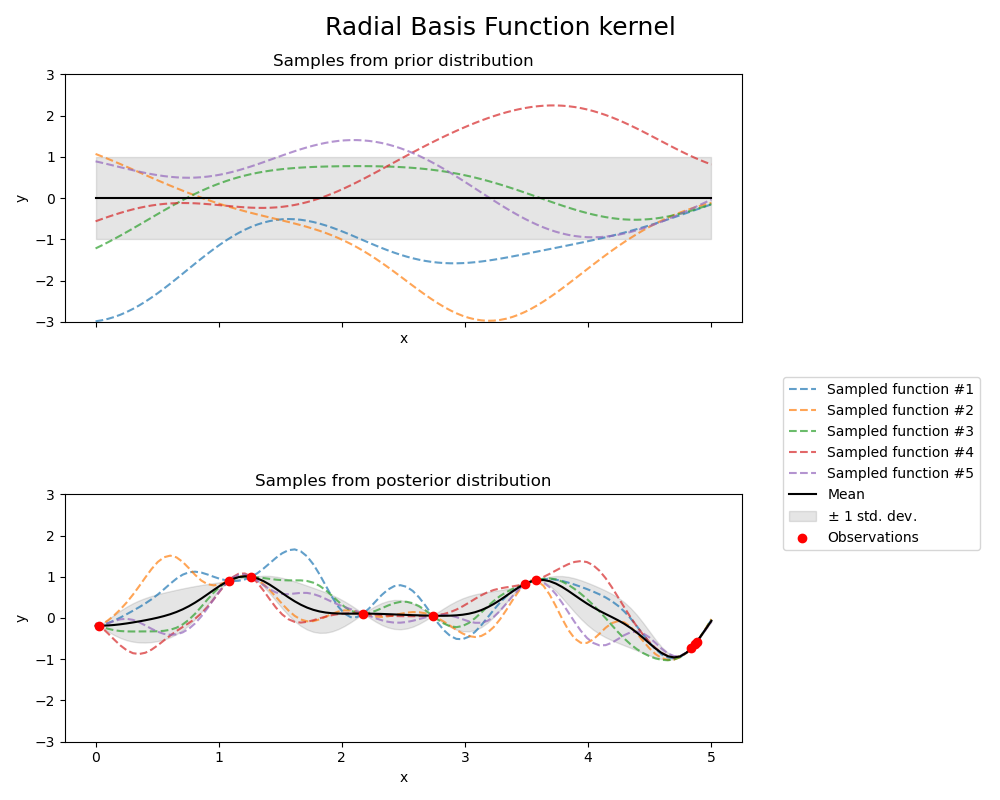
где \(d(\cdot, \cdot)\) это евклидово расстояние. Это ядро бесконечно дифференцируемо, что означает, что гауссовские процессы с этим ядром в качестве ковариационной функции имеют среднеквадратичные производные всех порядков и, таким образом, очень гладкие. Априорное и апостериорное распределения GP, полученные из ядра RBF, показаны на следующем рисунке:

1.7.4.4. Ядро Матерна

The Matern ядро является стационарным ядром и обобщением RBF ядро. Оно имеет дополнительный параметр \(\nu\) который контролирует гладкость результирующей функции. Он параметризуется параметром длины масштаба \(l>0\), который может быть либо скаляром (изотропный вариант ядра), либо вектором с тем же количеством измерений, что и входные данные \(x\) (анизотропный вариант ядра).

Математическая реализация ядра Матерна

Ядро задается:

\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)^\nu K_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg),\]

где \(d(\cdot,\cdot)\) это евклидово расстояние, \(K_\nu(\cdot)\) является модифицированной функцией Бесселя и \(\Gamma(\cdot)\) это гамма-функция. Поскольку \(\nu\rightarrow\infty\), ядро Матерна сходится к ядру RBF. Когда \(\nu = 1/2\), ядро Матерна становится идентичным абсолютному экспоненциальному ядру, т.е.,

\[k(x_i, x_j) = \exp \Bigg(- \frac{1}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}\]

В частности, \(\nu = 3/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x_i , x_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}\]

и \(\nu = 5/2\):

\[k(x_i, x_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x_i , x_j ) +\frac{5}{3l} d(x_i , x_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x_i , x_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}\]

являются популярными вариантами для функций обучения, которые не являются бесконечно дифференцируемыми (как предполагается ядром RBF), но по крайней мере один раз (\(\nu = 3/2\)) или дважды дифференцируема (\(\nu = 5/2\)).

Гибкость управления гладкостью изученной функции через \(\nu\) позволяет адаптироваться к свойствам истинной лежащей в основе функциональной зависимости.

Априорное и апостериорное распределения гауссовского процесса, полученные из ядра Матерна, показаны на следующем рисунке:

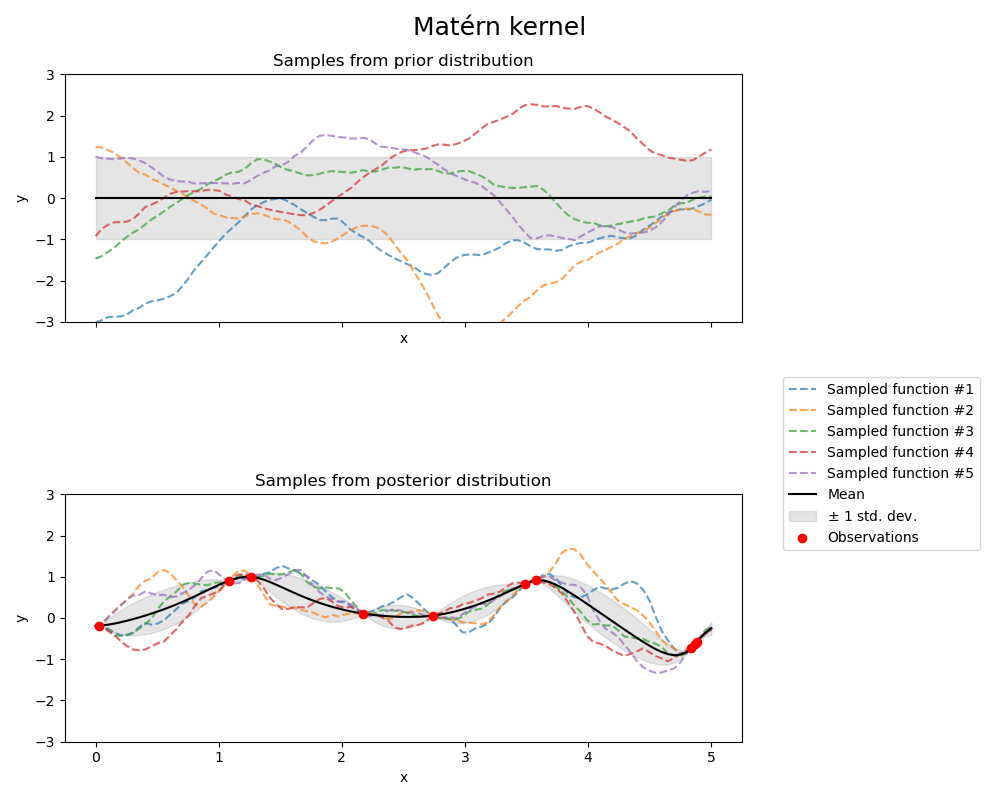
См. [RW2006], стр. 84 для дополнительных деталей относительно различных вариантов ядра Матерна.

1.7.4.5. Рациональное квадратичное ядро

The RationalQuadratic ядро можно рассматривать как масштабную смесь (бесконечную сумму) RBF ядра с разными характеристическими масштабами длины. Параметризуется параметром масштаба длины \(l>0\) и параметр масштабной смеси \(\alpha>0\) Только изотропный вариант, где \(l\) скаляр поддерживается на данный момент. Ядро задаётся как:

\[k(x_i, x_j) = \left(1 + \frac{d(x_i, x_j)^2}{2\alpha l^2}\right)^{-\alpha}\]

Априорное и апостериорное распределение гауссовского процесса, полученного из RationalQuadratic ядро показаны на следующем рисунке:

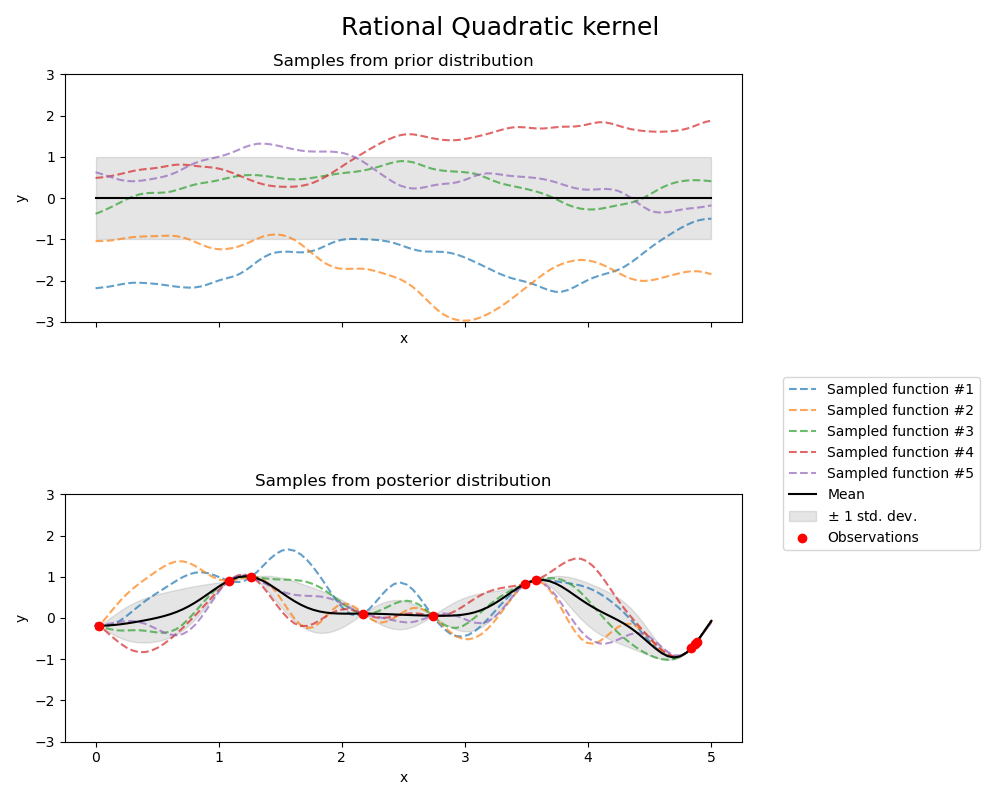
1.7.4.6. Ядро Exp-Sine-Squared

The ExpSineSquared ядро позволяет моделировать периодические функции. Оно параметризуется параметром масштаба длины \(l>0\) и параметр периодичности \(p>0\). Только изотропный вариант, где \(l\) скаляр поддерживается на данный момент. Ядро задаётся как:

\[k(x_i, x_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x_i, x_j) / p) }{ l^ 2} \right)\]

Априорное и апостериорное распределения гауссовского процесса, полученного из ядра ExpSineSquared, показаны на следующем рисунке:

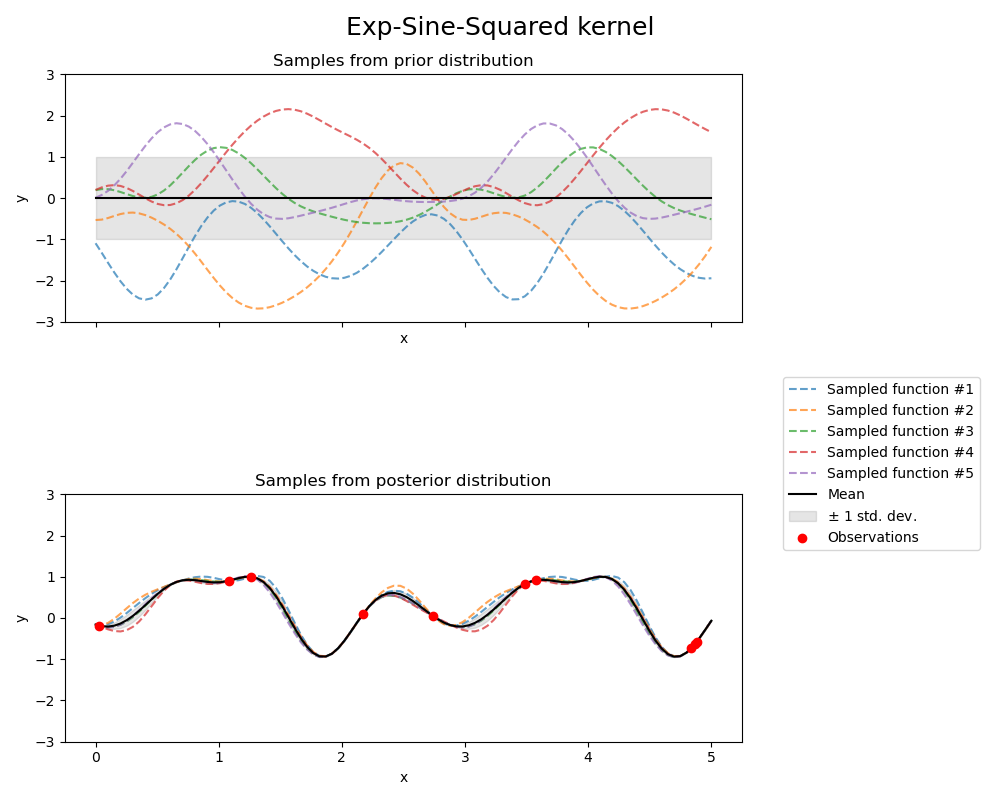
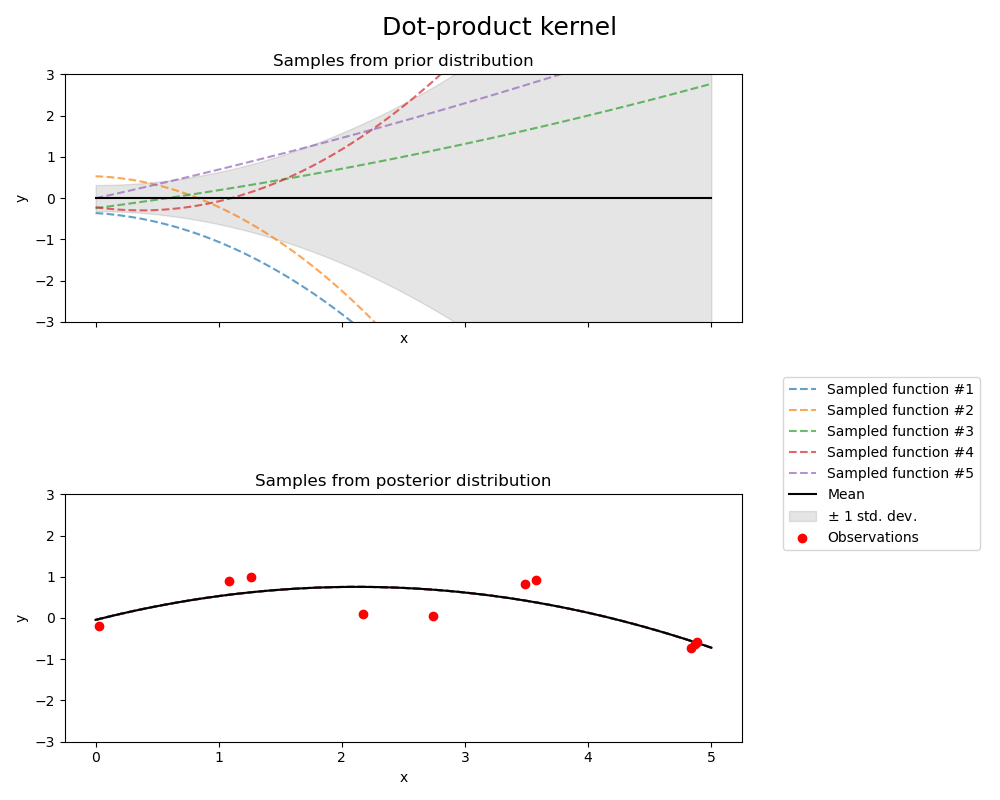
1.7.4.7. Ядро скалярного произведения

The DotProduct ядро является нестационарным и может быть получено из линейной регрессии путем помещения \(N(0, 1)\) априорные распределения на коэффициенты \(x_d (d = 1, . . . , D)\) и априорное распределение \(N(0, \sigma_0^2)\) на смещение. The DotProduct Ядро инвариантно к вращению координат относительно начала координат, но не к сдвигам. Оно параметризуется параметром \(\sigma_0^2\). Для \(\sigma_0^2 = 0\), ядро называется однородным линейным ядром, в противном случае оно неоднородно. Ядро задаётся формулой

\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]

The DotProduct ядро обычно комбинируется с возведением в степень. Пример с показателем степени 2 показан на следующем рисунке:

1.7.4.8. Ссылки

[RW2006] (1,2,3,4,5)

Карл Э. Расмуссен и Кристофер К.И. Уильямс, «Гауссовские процессы для машинного обучения», MIT Press 2006

[Duv2014]

Дэвид Дювено, "Поваренная книга ядер: Советы по ковариационным функциям", 2014