1.15. Изотоническая регрессия#
Класс IsotonicRegression подгоняет неубывающую вещественную функцию к одномерным данным. Она решает следующую задачу:
при условии \(\hat{y}_i \le \hat{y}_j\) всякий раз, когда \(X_i \le X_j\),
где веса \(w_i\) строго положительны, и оба X и y являются произвольными вещественными величинами.
The increasing параметр изменяет ограничение на
\(\hat{y}_i \ge \hat{y}_j\) всякий раз, когда \(X_i \le X_j\). Установка значения 'auto' автоматически выберет ограничение на основе коэффициент ранговой корреляции Спирмена.
IsotonicRegression производит серию предсказаний
\(\hat{y}_i\) для обучающих данных, которые ближе всего к целевым значениям
\(y\) в терминах среднеквадратичной ошибки. Эти прогнозы интерполируются
для предсказания на невидимых данных. Прогнозы IsotonicRegression
таким образом формируют функцию, которая является кусочно-линейной:
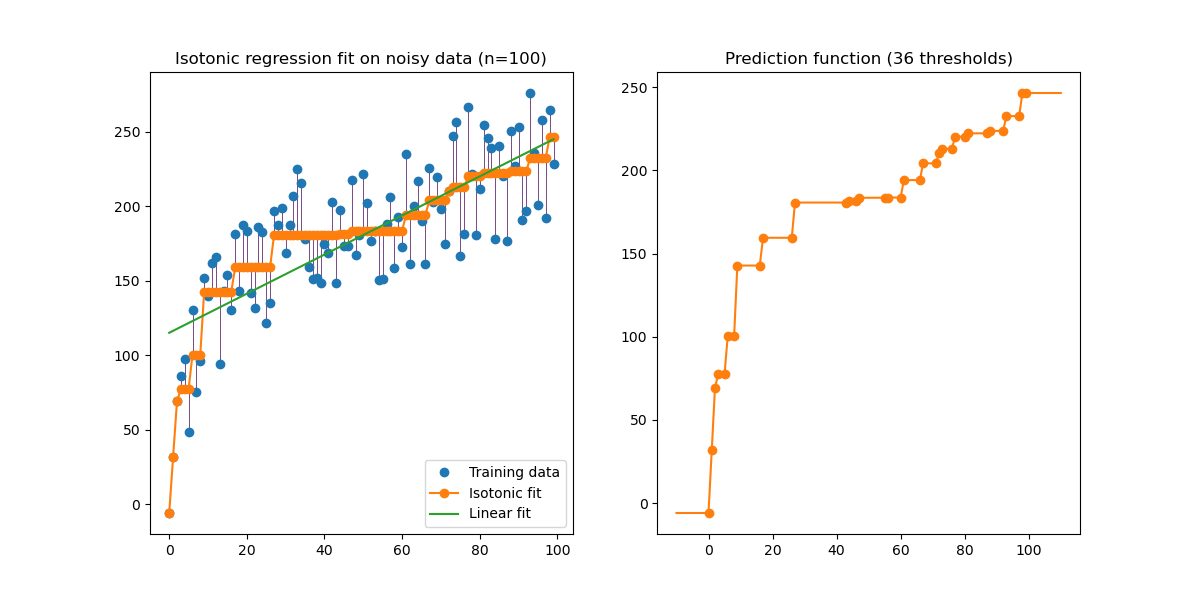
Примеры