2.2. Обучение многообразию

Ищите самое необходимое

Простые необходимые вещи

Забудьте о своих заботах и раздорах

Я имею в виду самое необходимое

Рецепты Матери-Природы

Которые приносят основные жизненные потребности

– Baloo’s song [The Jungle Book]

Многообразие обучения — это подход к нелинейному уменьшению размерности. Алгоритмы для этой задачи основаны на идее, что размерность многих наборов данных является лишь искусственно высокой.

2.2.1. Введение

Наборы данных высокой размерности могут быть очень сложными для визуализации. Хотя данные в двух или трех измерениях можно построить, чтобы показать внутреннюю структуру данных, эквивалентные графики высокой размерности гораздо менее интуитивны. Чтобы помочь визуализации структуры набора данных, размерность должна быть каким-то образом уменьшена.

Самый простой способ выполнить это снижение размерности — взять случайную проекцию данных. Хотя это позволяет в некоторой степени визуализировать структуру данных, случайность выбора оставляет желать лучшего. В случайной проекции вероятно, что более интересная структура данных будет утеряна.

Для решения этой проблемы было разработано несколько контролируемых и неконтролируемых линейных фреймворков уменьшения размерности, таких как метод главных компонент (PCA), метод независимых компонент, линейный дискриминантный анализ и другие. Эти алгоритмы определяют конкретные правила для выбора «интересной» линейной проекции данных. Эти методы могут быть мощными, но часто упускают важную нелинейную структуру в данных.

Обучение многообразий можно рассматривать как попытку обобщить линейные подходы, такие как PCA, чтобы они были чувствительны к нелинейной структуре в данных. Хотя существуют контролируемые варианты, типичная задача обучения многообразий является неконтролируемой: она изучает высокоразмерную структуру данных из самих данных, без использования заранее определённых классификаций.

Примеры

• См. Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap… для примера уменьшения размерности на рукописных цифрах.

• См. Сравнение методов обучения многообразий для примера снижения размерности на игрушечном наборе данных "S-кривая".

• См. Визуализация структуры фондового рынка для примера использования обучения многообразию для отображения структуры фондового рынка на основе исторических цен акций.

• См. Методы обучения многообразий на разрезанной сфере для примера применения методов обучения многообразий к сферическому набору данных.

• См. Снижение размерности Swiss Roll и Swiss-Hole для примера использования методов обучения многообразий на наборе данных Swiss Roll.

Реализации обучения многообразию, доступные в scikit-learn, суммированы ниже

2.2.2. SokalMichenerDistance

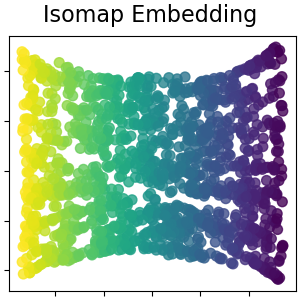
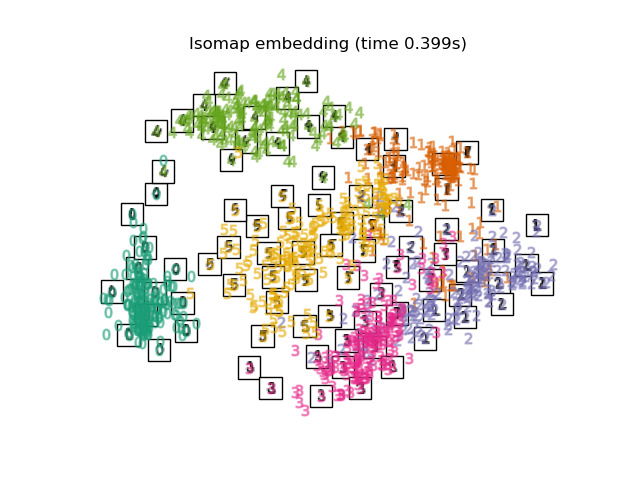
Одним из самых ранних подходов к обучению многообразий является алгоритм Isomap, сокращение от Isometric Mapping. Isomap можно рассматривать как расширение многомерного шкалирования (MDS) или Kernel PCA. Isomap ищет вложение меньшей размерности, которое сохраняет геодезические расстояния между всеми точками. Isomap может быть выполнен с объектом Isomap.

Сложность

Алгоритм Isomap состоит из трех этапов:

1. Поиск ближайшего соседа. Isomap использует BallTree для эффективного поиска соседей. Стоимость составляет приблизительно \(O[D \log(k) N \log(N)]\), для \(k\) ближайшие соседи \(N\) точки в \(D\) измерения.

2. Поиск кратчайшего пути в графе. Наиболее эффективные известные алгоритмы для этого Алгоритм Дейкстры, что приблизительно \(O[N^2(k + \log(N))]\), или Алгоритм Флойда-Уоршелла, который \(O[N^3]\). Алгоритм может быть выбран пользователем с помощью path_method ключевое слово Isomap. Если не указано, код пытается выбрать лучший алгоритм для входных данных.

3. Частичное разложение по собственным значениям. Вложение кодируется в собственных векторах, соответствующих \(d\) наибольшие собственные значения \(N \times N\) ядро isomap. Для плотного решателя стоимость составляет примерно \(O[d N^2]\). Эта стоимость часто может быть улучшена с использованием ARPACK решатель. Пользователь может указать решатель собственных значений с помощью eigen_solver ключевое слово Isomap. Если не указано, код пытается выбрать лучший алгоритм для входных данных.

Общая сложность Isomap составляет \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• “A global geometric framework for nonlinear dimensionality reduction” Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

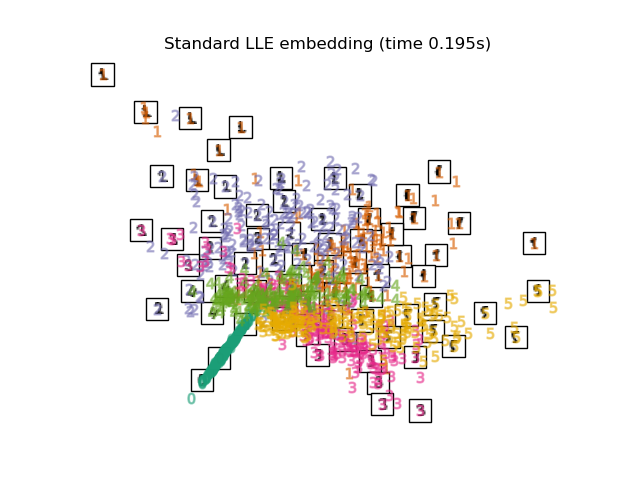
2.2.3. Локально-линейное вложение

Локально линейное вложение (LLE) ищет проекцию данных в пространство меньшей размерности, которая сохраняет расстояния внутри локальных окрестностей. Его можно рассматривать как серию локальных анализов главных компонент, которые глобально сравниваются для нахождения наилучшего нелинейного вложения.

Локально линейное вложение может быть выполнено с помощью функции locally_linear_embedding или его объектно-ориентированный аналог LocallyLinearEmbedding.

Сложность

Стандартный алгоритм LLE состоит из трех этапов:

1. Поиск ближайших соседей. См. обсуждение под Isomap выше.

2. Построение весовой матрицы. \(O[D N k^3]\). Построение матрицы весов LLE включает решение \(k \times k\) линейное уравнение для каждого из \(N\) локальные окрестности.

3. Частичное разложение по собственным значениям. См. обсуждение в разделе Isomap выше.

Общая сложность стандартного LLE составляет \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• «Nonlinear dimensionality reduction by locally linear embedding» Roweis, S. & Saul, L. Science 290:2323 (2000)

2.2.4. Modified Locally Linear Embedding

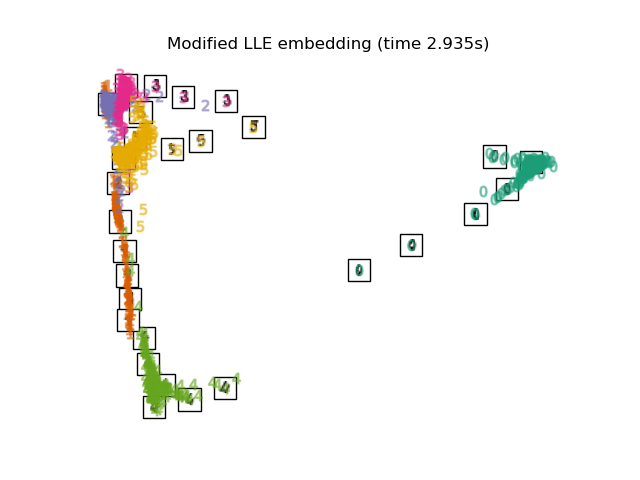
Известная проблема с LLE - проблема регуляризации. Когда количество соседей больше количества входных измерений, матрица, определяющая каждое локальное соседство, является вырожденной. Чтобы решить эту проблему, стандартный LLE применяет произвольный параметр регуляризации \(r\), который выбирается относительно следа локальной весовой матрицы. Хотя формально можно показать, что при \(r \to 0\), решение сходится к желаемому вложению, нет гарантии, что оптимальное решение будет найдено для \(r > 0\). Эта проблема проявляется во вложениях, которые искажают базовую геометрию многообразия.

Один из методов решения проблемы регуляризации — использование нескольких векторов весов в каждом соседстве. Это суть модифицированным локально линейным вложением (MLLE). MLLE может быть выполнена с функцией locally_linear_embedding или его объектно-ориентированный аналог LocallyLinearEmbedding, с ключевым словом method = 'modified'. Требуется n_neighbors > n_components.

Сложность

Алгоритм MLLE состоит из трех этапов:

1. Поиск ближайших соседей. То же, что и стандартный LLE

2. Построение весовой матрицы. Приблизительно \(O[D N k^3] + O[N (k-D) k^2]\). Первый член точно эквивалентен таковому в стандартном LLE. Второй член связан с построением матрицы весов из нескольких весов. На практике, дополнительная стоимость построения матрицы весов MLLE относительно мала по сравнению с стоимостью этапов 1 и 3.

3. Частичное разложение по собственным значениям. То же, что и стандартный LLE

Общая сложность MLLE составляет \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• “MLLE: Modified Locally Linear Embedding Using Multiple Weights” Zhang, Z. & Wang, J.

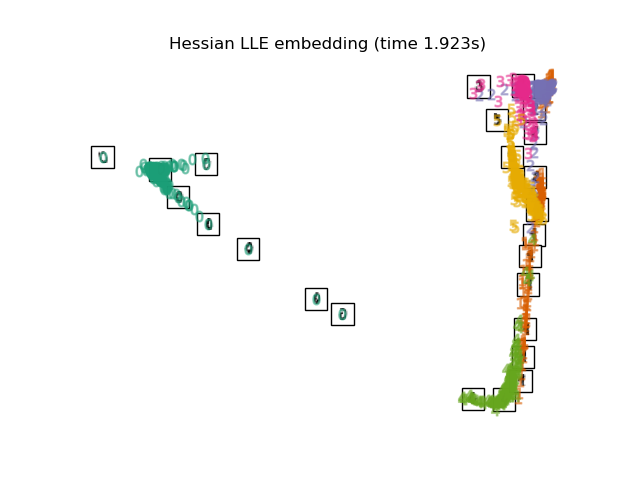
2.2.5. Hessian Eigenmapping

Отображение собственных значений Гессиана (также известное как HLLE: LLE на основе Гессиана) — это другой метод решения проблемы регуляризации LLE. Он основан на квадратичной форме на основе Гессиана в каждой окрестности, которая используется для восстановления локально линейной структуры. Хотя другие реализации отмечают его плохую масштабируемость с размером данных, sklearn реализует некоторые алгоритмические улучшения, которые делают его стоимость сопоставимой с другими вариантами LLE для малой размерности вывода. HLLE может быть выполнен с функцией locally_linear_embedding или его объектно-ориентированный аналог LocallyLinearEmbedding, с ключевым словом method = 'hessian'. Требуется n_neighbors > n_components * (n_components + 3) / 2.

Сложность

Алгоритм HLLE состоит из трех этапов:

1. Поиск ближайших соседей. То же, что и стандартный LLE

2. Построение весовой матрицы. Приблизительно \(O[D N k^3] + O[N d^6]\). Первый член отражает аналогичную стоимость, как у стандартного LLE. Второй член происходит из QR- разложения локального оценщика гессиана.

3. Частичное разложение по собственным значениям. То же, что и стандартный LLE.

Общая сложность стандартного HLLE составляет \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• “Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data” Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

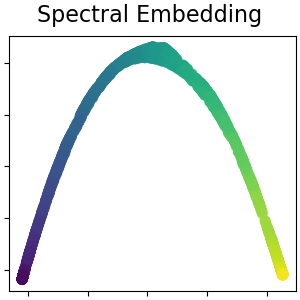
2.2.6. Спектральное вложение

Спектральное вложение — это подход к вычислению нелинейного вложения. Scikit-learn реализует лапласовы собственные отображения, которые находят низкоразмерное представление данных с использованием спектрального разложения графа Лапласиана. Сгенерированный граф можно рассматривать как дискретную аппроксимацию низкоразмерного многообразия в высокоразмерном пространстве. Минимизация функции стоимости на основе графа гарантирует, что точки, близкие друг к другу на многообразии, отображаются близко друг к другу в низкоразмерном пространстве, сохраняя локальные расстояния. Спектральное вложение может быть выполнено с помощью функции spectral_embedding или его объектно-ориентированный аналог SpectralEmbedding.

Сложность

Алгоритм спектрального вложения (Laplacian Eigenmaps) состоит из трех этапов:

1. Построение взвешенного графа. Преобразовать исходные входные данные в графовое представление с использованием матрицы сходства (смежности).

2. Построение лапласиана графа. Ненормализованный графовый лапласиан строится как \(L = D - A\) для и нормализованная как \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).

3. Частичное разложение по собственным значениям. Разложение по собственным значениям выполняется на лапласиане графа.

Общая сложность спектрального вложения составляет \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• “Laplacian Eigenmaps for Dimensionality Reduction and Data Representation” M. Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396.

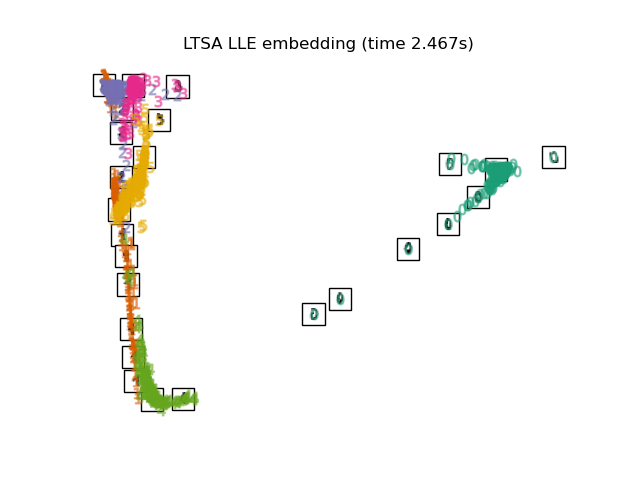
2.2.7. Локальное выравнивание касательного пространства

Хотя технически не является вариантом LLE, выравнивание локального касательного пространства (LTSA) алгоритмически достаточно похоже на LLE, чтобы его можно было отнести к этой категории. Вместо сохранения расстояний между соседями, как в LLE, LTSA стремится охарактеризовать локальную геометрию в каждом соседстве через его касательное пространство и выполняет глобальную оптимизацию для выравнивания этих локальных касательных пространств для изучения вложения. LTSA может быть выполнена с помощью функции locally_linear_embedding или его объектно-ориентированный аналог LocallyLinearEmbedding, с ключевым словом method = 'ltsa'.

Сложность

Алгоритм LTSA состоит из трех этапов:

1. Поиск ближайших соседей. То же, что и стандартный LLE

2. Построение весовой матрицы. Приблизительно \(O[D N k^3] + O[k^2 d]\). Первый член отражает аналогичную стоимость, как в стандартном LLE.

3. Частичное разложение по собственным значениям. То же, что и стандартный LLE

Общая сложность стандартного LTSA составляет \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).

• \(N\) : количество точек обучающих данных

• \(D\) : размерность ввода

• \(k\) : количество ближайших соседей

• \(d\) : размерность выхода

Ссылки

• "Главные многообразия и нелинейное снижение размерности через выравнивание касательного пространства" Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

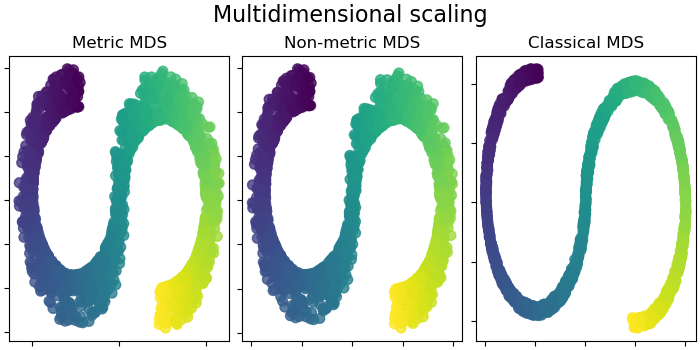
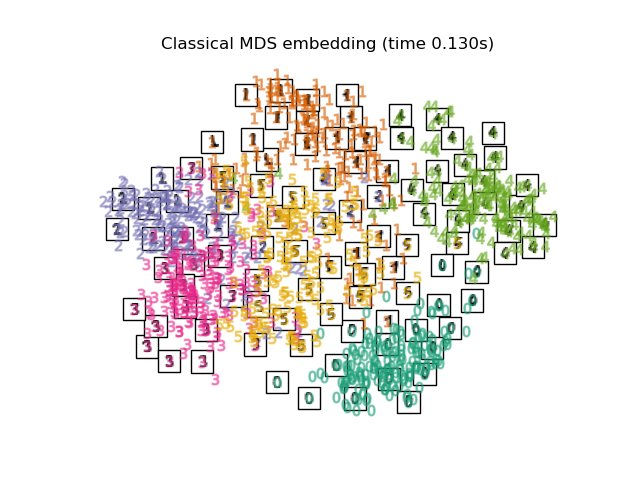
2.2.8. Многомерное шкалирование (MDS)

Многомерное шкалирование (MDS и ClassicalMDS) ищет низкоразмерное представление данных, в котором расстояния аппроксимируют расстояния в исходном высокоразмерном пространстве.

В общем, MDS – это техника, используемая для анализа данных несходства. Она пытается моделировать несходства как расстояния в евклидовом пространстве. Данные могут быть оценками несходства между объектами, частотами взаимодействия молекул или торговыми индексами между странами.

Существует три типа алгоритма MDS: метрический, неметрический и классический. В scikit-learn класс MDS реализует метрическое и неметрическое MDS, в то время как ClassicalMDS реализует классическое MDS. В метрическом MDS расстояния во встраиваемом пространстве устанавливаются как можно ближе к данным о несходстве. В неметрической версии алгоритм попытается сохранить порядок расстояний и, следовательно, будет искать монотонную зависимость между расстояниями во встроенном пространстве и входными несходствами. Наконец, классическое MDS близко к PCA и вместо аппроксимации расстояний аппроксимирует попарные скалярные произведения, что является более простой задачей оптимизации с аналитическим решением в терминах собственного разложения.

Пусть \(\delta_{ij}\) будет матрицей несходства между \(n\) входные точки (возможно, возникающие как некоторые попарные расстояния \(d_{ij}(X)\) между координатами \(X\) входных точек). Несоответствия \(\hat{d}_{ij} = f(\delta_{ij})\) являются некоторым преобразованием несходств. Целевая функция MDS, называемая сырым стрессом, затем определяется как \(\sum_{i < j} (\hat{d}_{ij} - d_{ij}(Z))^2\), где \(d_{ij}(Z)\) являются попарными расстояниями между координатами \(Z\) встроенных точек.

Метрический MDS

В метрике MDS модель (иногда также называемая абсолютное MDS), различия просто равны входным несходствам \(\hat{d}_{ij} = \delta_{ij}\).

Неметрическое MDS

Неметрический MDS фокусируется на упорядочении данных. Если \(\delta_{ij} > \delta_{kl}\), тогда вложение стремится обеспечить \(d_{ij}(Z) > d_{kl}(Z)\). Простой алгоритм для обеспечения правильного упорядочивания — использовать изотоническую регрессию \(d_{ij}(Z)\) на \(\delta_{ij}\), приводя к различиям \(\hat{d}_{ij}\) которые являются монотонным преобразованием несходств \(\delta_{ij}\) и, следовательно, имеющий тот же порядок. Это повторяется после каждого шага алгоритма оптимизации. Чтобы избежать тривиального решения, где все точки вложения перекрываются, несоответствия \(\hat{d}_{ij}\) нормализованы.

Обратите внимание, что поскольку нас интересует только относительный порядок, наша цель должна быть инвариантна к простому сдвигу и масштабированию, однако стресс, используемый в метрическом MDS, чувствителен к масштабированию. Чтобы решить это, неметрический MDS возвращает нормализованный стресс, также известный как Stress-1, определенный как

\[\sqrt{\frac{\sum_{i < j} (\hat{d}_{ij} - d_{ij}(Z))^2}{\sum_{i < j} d_{ij}(Z)^2}}.\]

Возвращается Normalized Stress-1, если normalized_stress=True.

Классический MDS, также известный как анализ главных координат (PCoA) или Масштабирование Торгерсона, реализован в отдельном ClassicalMDS класс. Классический MDS заменяет функцию потерь стресса на другую функцию потерь, называемую strain, который имеет точное решение в терминах собственного разложения. Если матрица несходства состоит из попарных евклидовых расстояний между некоторыми векторами, то классическое MDS эквивалентно применению PCA к этому набору векторов.

Формально функция потерь классического MDS (strain) задается как

\[\frac{\|B - ZZ^T\|_F}{\|B\|_F} =\sqrt{\frac{\sum_{i,j} (b_{ij} - z_i^\top z_j)^2}{\sum_{i,j} b_{ij}^2}},\]

где \(Z\) является \(n \times d\) матрица эмбеддингов, строки которой являются \(z_i^T\), \(\|\cdot\|_F\) обозначает норму Фробениуса, и \(B\) это матрица Грама с элементами \(b_{ij}\), заданный \(B = -\frac{1}{2}C\Delta C\). Здесь \(C\Delta C\) является дважды центрированной матрицей квадратов несходств, с \(\Delta\) является матрицей квадратов входных различий \(\delta^2_{ij}\) и \(C=I-J/n\) является центрирующей матрицей (единичная матрица минус матрица из всех единиц, деленная на \(n\)). Это можно минимизировать точно, используя собственное разложение \(B\).

Ссылки

• “More on Multidimensional Scaling and Unfolding in R: smacof Version 2” Mair P, Groenen P., de Leeuw J. Journal of Statistical Software (2022)

• “Modern Multidimensional Scaling - Theory and Applications” Borg, I.; Groenen P. Springer Series in Statistics (1997)

• “Неметрическое многомерное шкалирование: численный метод” Kruskal, J. Psychometrika, 29 (1964)

• “Многомерное шкалирование путём оптимизации соответствия неметрической гипотезе” Kruskal, J. Psychometrika, 29, (1964)

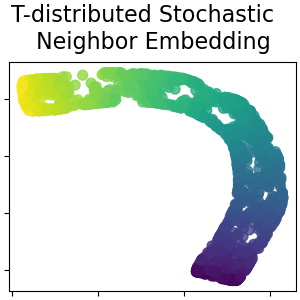
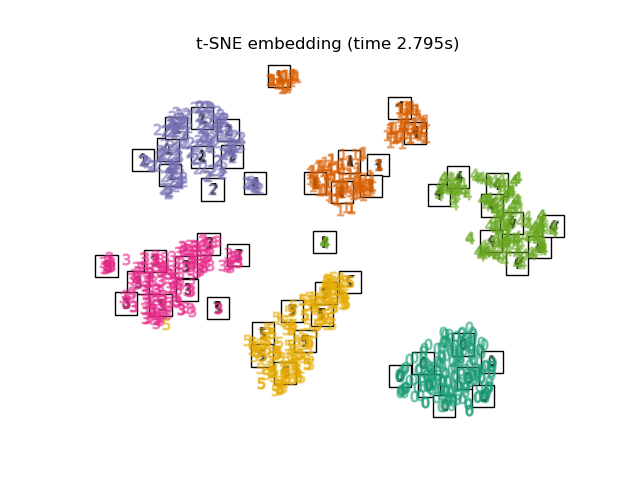
2.2.9. t-распределённое стохастическое вложение соседей (t-SNE)

t-SNE (TSNE) преобразует сходства точек данных в вероятности. Сходства в исходном пространстве представлены гауссовскими совместными вероятностями, а сходства во встроенном пространстве представлены t-распределениями Стьюдента. Это позволяет t-SNE быть особенно чувствительным к локальной структуре и имеет несколько других преимуществ по сравнению с существующими техниками:

• Раскрытие структуры на многих масштабах на одной карте

• Выявление данных, лежащих в нескольких различных многообразиях или кластерах

• Уменьшение тенденции к скоплению точек в центре

Хотя Isomap, LLE и их варианты лучше всего подходят для развёртывания одного непрерывного низкоразмерного многообразия, t-SNE фокусируется на локальной структуре данных и стремится извлекать сгруппированные локальные группы образцов, как показано на примере S-кривой. Эта способность группировать образцы на основе локальной структуры может быть полезна для визуального разделения набора данных, который включает несколько многообразий одновременно, как в случае с набором данных digits.

Расхождение Кульбака-Лейблера (KL) совместных вероятностей в исходном пространстве и вложенном пространстве будет минимизировано методом градиентного спуска. Заметим, что расхождение KL не является выпуклым, т.е. множественные перезапуски с разными инициализациями могут привести к локальным минимумам расхождения KL. Поэтому иногда полезно пробовать разные начальные значения и выбирать вложение с наименьшим расхождением KL.

Недостатки использования t-SNE примерно следующие:

• t-SNE вычислительно затратен и может занимать несколько часов на наборах данных с миллионами образцов, где PCA завершится за секунды или минуты

• Метод Barnes-Hut t-SNE ограничен двумерными или трехмерными вложениями.

• Алгоритм стохастический, и несколько перезапусков с разными начальными значениями могут давать различные вложения. Однако вполне допустимо выбрать вложение с наименьшей ошибкой.

• Глобальная структура явно не сохраняется. Эта проблема смягчается инициализацией точек с помощью PCA (используя init='pca').

Оптимизация t-SNE

Основная цель t-SNE — визуализация многомерных данных. Следовательно, он работает лучше всего, когда данные будут вложены в два или три измерения.

Оптимизация дивергенции Кульбака-Лейблера иногда может быть немного сложной. Есть пять параметров, которые управляют оптимизацией t-SNE и, следовательно, возможно, качеством получаемого вложения:

• перплексия

• коэффициент раннего преувеличения

• скорость обучения

• максимальное количество итераций

• угол (не используется в точном методе)

Перплексия определяется как \(k=2^{(S)}\) где \(S\) является энтропией Шеннона условного распределения вероятностей. Перплексия \(k\)-гранная кость \(k\), чтобы \(k\) фактически является количеством ближайших соседей, которые t-SNE учитывает при генерации условных вероятностей. Большие значения perplexity приводят к большему количеству ближайших соседей и меньшей чувствительности к мелкой структуре. И наоборот, меньшее значение perplexity учитывает меньшее количество соседей и, таким образом, игнорирует более глобальную информацию в пользу локальной окрестности. По мере увеличения размеров наборов данных потребуется больше точек, чтобы получить разумную выборку локальной окрестности, и, следовательно, могут потребоваться большие значения perplexity. Аналогично, более зашумленные наборы данных потребуют больших значений perplexity, чтобы охватить достаточно локальных соседей и увидеть за фоновым шумом.

Максимальное количество итераций обычно достаточно велико и не требует настройки. Оптимизация состоит из двух фаз: фазы раннего преувеличения и финальной оптимизации. Во время раннего преувеличения совместные вероятности в исходном пространстве искусственно увеличиваются умножением на заданный коэффициент. Большие коэффициенты приводят к большим разрывам между естественными кластерами в данных. Если коэффициент слишком высок, расхождение KL может увеличиться в этой фазе. Обычно его не нужно настраивать. Критический параметр — скорость обучения. Если она слишком низкая, градиентный спуск застрянет в плохом локальном минимуме. Если она слишком высокая, расхождение KL увеличится во время оптимизации. Эвристика, предложенная в Belkina et al. (2019), заключается в установке скорости обучения равной размеру выборки, делённому на коэффициент раннего преувеличения. Мы реализуем эту эвристику как learning_rate='auto' аргумент. Дополнительные советы можно найти в FAQ Лоренса ван дер Маатена (см. ссылки). Последний параметр, угол, представляет собой компромисс между производительностью и точностью. Большие углы подразумевают, что мы можем аппроксимировать большие области одной точкой, что приводит к лучшей скорости, но менее точным результатам.

“Как эффективно использовать t-SNE” предоставляет хорошее обсуждение эффектов различных параметров, а также интерактивные графики для изучения эффектов разных параметров.

Barnes-Hut t-SNE

Реализованный здесь t-SNE Барнса-Хата обычно намного медленнее, чем другие алгоритмы обучения многообразию. Оптимизация довольно сложна, и вычисление градиента \(O[d N log(N)]\), где \(d\) — это количество выходных размерностей, а \(N\) — это количество выборок. Метод Barnes-Hut улучшает точный метод, где сложность t-SNE составляет \(O[d N^2]\), но имеет несколько других заметных отличий:

• Реализация Барнса-Хата работает только когда целевая размерность равна 3 или меньше. 2D случай типичен при построении визуализаций.

• Barnes-Hut работает только с плотными входными данными. Разреженные матрицы данных могут быть встроены только с помощью точного метода или могут быть аппроксимированы плотной низкоранговой проекцией, например, используя PCA

• Barnes-Hut — это аппроксимация точного метода. Аппроксимация параметризуется угловым параметром, поэтому угловой параметр не используется, когда method="exact"

• Barnes-Hut значительно более масштабируем. Barnes-Hut может использоваться для встраивания сотен тысяч точек данных, в то время как точный метод может обрабатывать тысячи образцов до того, как станет вычислительно неразрешимым

Для целей визуализации (что является основным случаем использования t-SNE) использование метода Barnes-Hut настоятельно рекомендуется. Точный метод t-SNE полезен для проверки теоретических свойств вложения, возможно, в пространстве более высокой размерности, но ограничен небольшими наборами данных из-за вычислительных ограничений.

Также обратите внимание, что метки цифр примерно соответствуют естественной группировке, найденной t-SNE, в то время как линейная 2D проекция модели PCA дает представление, где области меток в значительной степени перекрываются. Это сильный признак того, что эти данные могут быть хорошо разделены нелинейными методами, которые фокусируются на локальной структуре (например, SVM с гауссовым ядром RBF). Однако неудача в визуализации хорошо разделенных однородно помеченных групп с помощью t-SNE в 2D не обязательно означает, что данные не могут быть правильно классифицированы контролируемой моделью. Возможно, что 2 измерения недостаточно высоки для точного представления внутренней структуры данных.

Ссылки

• «Визуализация высокоразмерных данных с использованием t-SNE» van der Maaten, L.J.P.; Hinton, G. Journal of Machine Learning Research (2008)

• «Стохастическое вложение соседей с t-распределением» ван дер Маатен, Л.Дж.П.

• «Ускорение t-SNE с использованием древовидных алгоритмов» van der Maaten, L.J.P.; Journal of Machine Learning Research 15(Oct):3221-3245, 2014.

• “Автоматизированные оптимизированные параметры для стохастического вложения соседей с t-распределением улучшают визуализацию и анализ больших наборов данных” Belkina, A.C., Ciccolella, C.O., Anno, R., Halpert, R., Spidlen, J., Snyder-Cappione, J.E., Nature Communications 10, 5415 (2019).

2.2.10. Советы по практическому использованию

• Убедитесь, что используется один и тот же масштаб для всех признаков. Поскольку методы обучения многообразий основаны на поиске ближайших соседей, алгоритм может работать плохо в противном случае. См. StandardScaler для удобных способов масштабирования разнородных данных.

• Ошибка реконструкции, вычисляемая каждой процедурой, может быть использована для выбора оптимальной размерности выходных данных. Для \(d\)-мерное многообразие, вложенное в \(D\)-мерном пространстве параметров, ошибка реконструкции будет уменьшаться по мере n_components увеличивается до тех пор, пока n_components == d.

• Обратите внимание, что зашумленные данные могут "закорачивать" многообразие, по сути действуя как мост между частями многообразия, которые в противном случае были бы хорошо разделены. Обучение на многообразиях на зашумленных и/или неполных данных является активной областью исследований.

• Модели нейронных сетей (с учителем) solver='arpack' не сможет найти нулевое пространство. Самый простой способ решить эту проблему - использовать solver='dense' которая будет работать с сингулярной матрицей, хотя это может быть очень медленно в зависимости от количества входных точек. В качестве альтернативы можно попытаться понять источник сингулярности: если она вызвана непересекающимися множествами, увеличение n_neighbors может помочь. Если это связано с идентичными точками в наборе данных, их удаление может помочь.

Смотрите также

Полностью случайные деревья вложения также может быть полезен для получения нелинейных представлений пространства признаков, но не выполняет снижение размерности.