5.1. Графики частичной зависимости и индивидуального условного ожидания#

Графики частичной зависимости (PDP) и графики индивидуального условного ожидания (ICE) могут использоваться для визуализации и анализа взаимодействия между целевым откликом [1] и набору интересующих входных признаков.

Обе PDP [H2009] и ICEs [G2015] предполагается, что интересующие входные признаки независимы от дополнительных признаков, и это предположение часто нарушается на практике. Таким образом, в случае коррелированных признаков мы будем создавать абсурдные точки данных для вычисления PDP/ICE [M2019].

5.1.1. Графики частных зависимостей#

Графики частичной зависимости (PDP) показывают зависимость между целевым откликом и набором интересующих входных признаков, маргинализируя по значениям всех других входных признаков (признаков-‘дополнений’). Интуитивно, мы можем интерпретировать частичную зависимость как ожидаемый целевой отклик как функцию интересующих входных признаков.

Из-за ограничений человеческого восприятия размер множества интересующих входных признаков должен быть небольшим (обычно один или два), поэтому интересующие входные признаки обычно выбираются среди наиболее важных признаков.

На рисунке ниже показаны два односторонних и один двусторонний график частичной зависимости для набора данных о прокате велосипедов, с HistGradientBoostingRegressor:

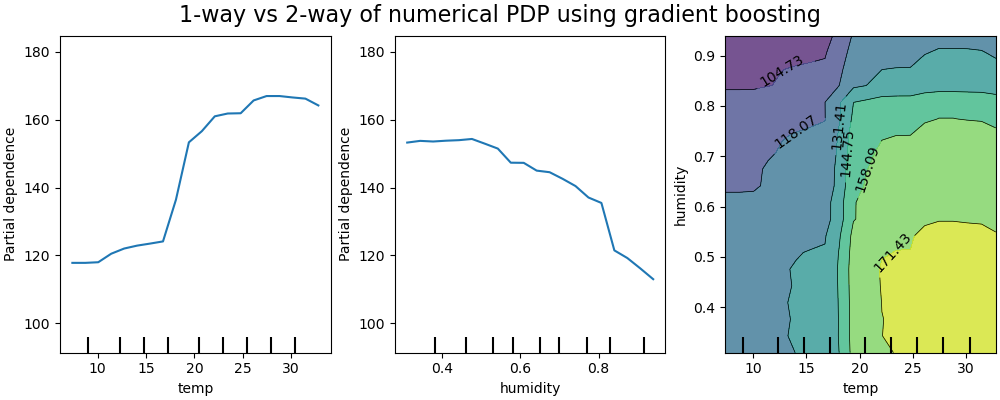
../_images/sphx_glr_plot_partial_dependence_006.png

Одномерные PDP (Partial Dependence Plots) показывают взаимодействие между целевым откликом и интересующим входным признаком (например, линейное, нелинейное). Левый график на рисунке выше показывает влияние температуры на количество прокатов велосипедов; мы ясно видим, что более высокая температура связана с большим количеством прокатов. Аналогично мы можем проанализировать влияние влажности на количество прокатов велосипедов (средний график). Таким образом, эти интерпретации являются маргинальными, рассматривая один признак за раз.

PDP с двумя входными признаками интереса показывают взаимодействия между двумя признаками. Например, двухпеременный PDP на рисунке выше показывает зависимость количества прокатов велосипедов от совместных значений температуры и влажности. Мы ясно видим взаимодействие между двумя признаками: при температуре выше 20 градусов Цельсия, в основном влажность сильно влияет на количество прокатов велосипедов. Для более низких температур, и температура, и влажность влияют на количество прокатов велосипедов.

The sklearn.inspection модуль предоставляет удобную функцию from_estimator для создания одномерных и двумерных графиков частичной зависимости. В примере ниже мы показываем, как создать сетку графиков частичной зависимости: два одномерных графика для признаков 0 и 1 и двусторонний PDP между двумя признаками:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import PartialDependenceDisplay

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1, (0, 1)]
>>> PartialDependenceDisplay.from_estimator(clf, X, features)
<...>

Вы можете получить доступ к недавно созданным объектам Figure и Axes, используя plt.gcf() и plt.gca().

Чтобы построить график частичной зависимости с категориальными признаками, необходимо указать какие признаки являются категориальными, используя параметр categorical_features. Этот параметр принимает список индексов, имена категориальных признаков или булеву маску. Графическое представление частной зависимости для категориальных признаков — это столбчатая диаграмма или 2D тепловая карта.

PDP для многоклассовой классификации#

Для многоклассовой классификации необходимо установить метку класса, для которой должны быть созданы ЧРЗ, через target аргумент:

>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> mc_clf = GradientBoostingClassifier(n_estimators=10,
...     max_depth=1).fit(iris.data, iris.target)
>>> features = [3, 2, (3, 2)]
>>> PartialDependenceDisplay.from_estimator(mc_clf, X, features, target=0)
<...>

Тот же параметр target используется для указания цели в многозадачных регрессионных настройках.

Если вам нужны исходные значения функции частичной зависимости, а не графики, вы можете использовать sklearn.inspection.partial_dependence функция:

>>> from sklearn.inspection import partial_dependence

>>> results = partial_dependence(clf, X, [0])
>>> results["average"]
array([[ 2.466...,  2.466..., ...
>>> results["grid_values"]
[array([-1.624..., -1.592..., ...

Значения, при которых должна оцениваться частичная зависимость, генерируются непосредственно из X. Для двусторонней частной зависимости генерируется 2D-сетка значений. Параметр values поле, возвращаемое sklearn.inspection.partial_dependence дает фактические значения, используемые в сетке для каждого интересующего входного признака. Они также соответствуют осям графиков.

5.1.2. График индивидуального условного ожидания (ICE)#

Подобно PDP, график индивидуального условного ожидания (ICE) показывает зависимость между целевой функцией и интересующим входным признаком. Однако, в отличие от PDP, который показывает средний эффект входного признака, график ICE визуализирует зависимость предсказания от признака для каждого образца отдельно, с одной линией на образец. Из-за ограничений человеческого восприятия для графиков ICE поддерживается только один интересующий входной признак.

На рисунках ниже показаны два графика ICE для набора данных о прокате велосипедов, с HistGradientBoostingRegressor. На графиках соответствующая линия PD наложена на линии ICE.

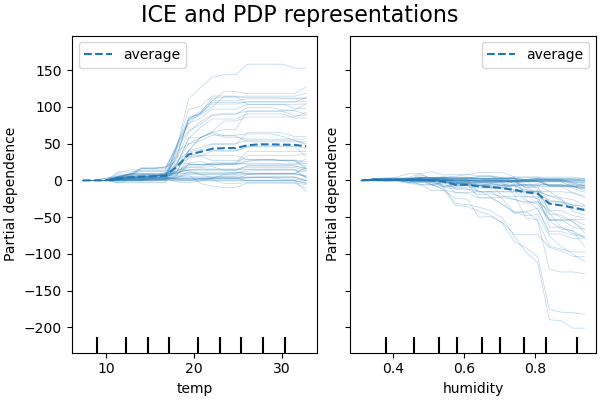
../_images/sphx_glr_plot_partial_dependence_004.png

Хотя графики частных зависимостей хорошо показывают средний эффект целевых признаков, они могут скрывать неоднородные отношения, создаваемые взаимодействиями. При наличии взаимодействий график ICE предоставит гораздо больше информации. Например, мы видим, что график ICE для признака температуры дает нам дополнительную информацию: некоторые линии ICE плоские, а другие показывают уменьшение зависимости для температуры выше 35 градусов Цельсия. Мы наблюдаем аналогичную закономерность для признака влажности: некоторые линии ICE показывают резкое снижение, когда влажность превышает 80%.

The sklearn.inspection модуля PartialDependenceDisplay.from_estimator удобная функция может использоваться для создания ICE-графиков, установив kind='individual'. В примере ниже мы показываем, как создать сетку графиков ICE:

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> from sklearn.inspection import PartialDependenceDisplay

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> features = [0, 1]
>>> PartialDependenceDisplay.from_estimator(clf, X, features,
...     kind='individual')
<...>

В графиках ICE может быть непросто увидеть средний эффект интересующего входного признака. Поэтому рекомендуется использовать графики ICE вместе с PDP. Их можно построить вместе с kind='both'.

>>> PartialDependenceDisplay.from_estimator(clf, X, features,
...     kind='both')
<...>

Если в графике ICE слишком много линий, может быть трудно увидеть различия между отдельными образцами и интерпретировать модель. Центрирование ICE по первому значению на оси x создает центрированные графики индивидуальных условных ожиданий (cICE) [G2015]. Это делает акцент на расхождении индивидуальных условных ожиданий от средней линии, что облегчает исследование неоднородных отношений. Графики cICE можно построить, установив centered=True:

>>> PartialDependenceDisplay.from_estimator(clf, X, features,
...     kind='both', centered=True)
<...>

5.1.3. Математическое определение#

Пусть \(X_S\) будет набором входных признаков, представляющих интерес (т.е. features параметр) и пусть \(X_C\) будет его дополнением.

Частная зависимость отклика \(f\) в точке \(x_S\) определяется как:

\[\begin{split}pd_{X_S}(x_S) &\overset{def}{=} \mathbb{E}_{X_C}\left[ f(x_S, X_C) \right]\\ &= \int f(x_S, x_C) p(x_C) dx_C,\end{split}\]

где \(f(x_S, x_C)\) является функцией отклика (predict, predict_proba или decision_function) для данного образца, значения которого определены \(x_S\) для признаков в \(X_S\), и благодаря \(x_C\) для признаков в \(X_C\). Обратите внимание, что \(x_S\) и \(x_C\) могут быть кортежами.

Вычисление этого интеграла для различных значений \(x_S\) создаёт график PDP, как показано выше. Линия ICE определяется как отдельная \(f(x_{S}, x_{C}^{(i)})\) вычислено в \(x_{S}\).

5.1.4. Методы вычислений#

Существует два основных метода аппроксимации приведённого выше интеграла, а именно 'brute' и 'recursion' методы. Параметр method параметр управляет тем, какой метод использовать.

The 'brute' метод является универсальным методом, который работает с любым оценщиком. Обратите внимание, что вычисление ICE графиков поддерживается только с 'brute' метод. Он аппроксимирует указанный выше интеграл, вычисляя среднее по данным X:

\[pd_{X_S}(x_S) \approx \frac{1}{n_\text{samples}} \sum_{i=1}^n f(x_S, x_C^{(i)}),\]

где \(x_C^{(i)}\) является значением i-го образца для признаков в \(X_C\). Для каждого значения \(x_S\), этот метод требует полного прохода по набору данных X что требует больших вычислительных затрат.

Каждый из \(f(x_{S}, x_{C}^{(i)})\) соответствует одной линии ICE, вычисленной в \(x_{S}\)Вычисление этого для нескольких значений \(x_{S}\), получается полная линия ICE. Как видно, среднее линий ICE соответствует линии частичной зависимости.

The 'recursion' метод быстрее, чем 'brute' метод, но он поддерживается только для PDP графиков некоторыми древовидными оценщиками. Он вычисляется следующим образом. Для данной точки \(x_S\), выполняется взвешенный обход дерева: если узел разделения включает интересующий входной признак, следует соответствующая левая или правая ветвь; в противном случае следуют обе ветви, каждая взвешивается по доле обучающих образцов, попавших в эту ветвь. Наконец, частичная зависимость задаётся взвешенным средним значений всех посещённых листьев.

С 'brute' метод, параметр X используется как для генерации сетки значений \(x_S\) и дополнительные значения признаков \(x_C\)Однако с методом 'recursion', X используется только для значений сетки: неявно, \(x_C\) значения — это значения обучающих данных.

По умолчанию, 'recursion' метод используется для построения PDP на древовидных оценщиках, которые его поддерживают, а 'brute' используется для остальных.

Примечание

Хотя оба метода должны быть близки в целом, они могут различаться в некоторых конкретных настройках. 'brute' метод предполагает существование точек данных \((x_S, x_C^{(i)})\). Когда признаки коррелированы, такие искусственные выборки могут иметь очень низкую вероятность. 'brute' и 'recursion' методы, вероятно, будут расходиться относительно значения частичной зависимости, потому что они будут обрабатывать эти маловероятные выборки по-разному. Помните, однако, что основное предположение для интерпретации PDPs заключается в том, что признаки должны быть независимыми.

Примеры

Сноски

Ссылки

[H2009]

T. Hastie, R. Tibshirani и J. Friedman, The Elements of Statistical Learning, Второе издание, Раздел 10.13.2, Springer, 2009.