3.1. Кросс-валидация: оценка производительности оценщика

Изучение параметров прогнозной функции и тестирование ее на тех же данных является методологической ошибкой: модель, которая просто повторяет метки выборок, которые она только что видела, имела бы идеальный результат, но не смогла бы предсказать что-либо полезное на еще невиданных данных. Эта ситуация называется переобучение. Чтобы избежать этого, общепринятой практикой при проведении (контролируемого) эксперимента машинного обучения является выделение части доступных данных в качестве тестовый набор X_test, y_test. Обратите внимание, что слово «эксперимент» не предназначено для обозначения только академического использования, потому что даже в коммерческих условиях машинное обучение обычно начинается экспериментально. 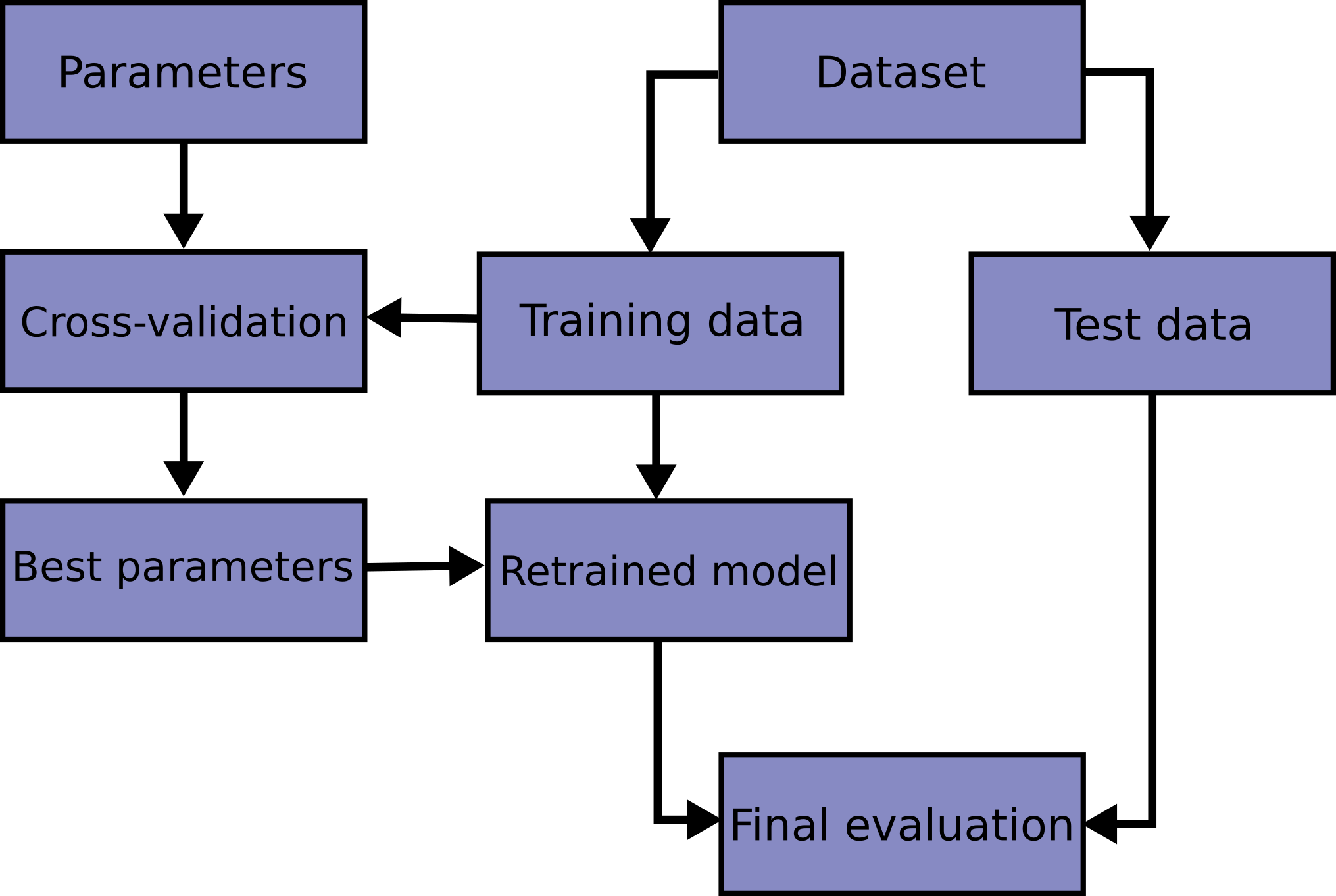Вот блок-схема типичного процесса перекрестной проверки при обучении модели. Лучшие параметры могут быть определены с помощью grid search методы.

В scikit-learn случайное разделение на обучающую и тестовую выборки можно быстро вычислить с помощью train_test_split вспомогательная функция. Давайте загрузим набор данных iris, чтобы обучить на нем линейную машину опорных векторов:

>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm

>>> X, y = datasets.load_iris(return_X_y=True)
>>> X.shape, y.shape
((150, 4), (150,))

Теперь мы можем быстро выбрать обучающую выборку, оставив 40% данных для тестирования (оценки) нашего классификатора:

>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)

>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))

>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96

При оценке различных настроек ("гиперпараметров") для оценщиков, таких как C параметр, который должен быть установлен вручную для SVM, все еще существует риск переобучения на тестовом наборе потому что параметры могут быть настроены до тех пор, пока оценщик не будет работать оптимально. Таким образом, знания о тестовом наборе могут "просочиться" в модель, и метрики оценки больше не сообщают о производительности обобщения. Чтобы решить эту проблему, еще одна часть набора данных может быть выделена в качестве так называемого "валидационного набора": обучение происходит на обучающем наборе, после чего оценка выполняется на валидационном наборе, и когда эксперимент кажется успешным, окончательная оценка может быть выполнена на тестовом наборе.

Однако, разделяя доступные данные на три множества, мы резко сокращаем количество образцов, которые могут быть использованы для обучения модели, и результаты могут зависеть от конкретного случайного выбора пары (обучающее, валидационное) множеств.

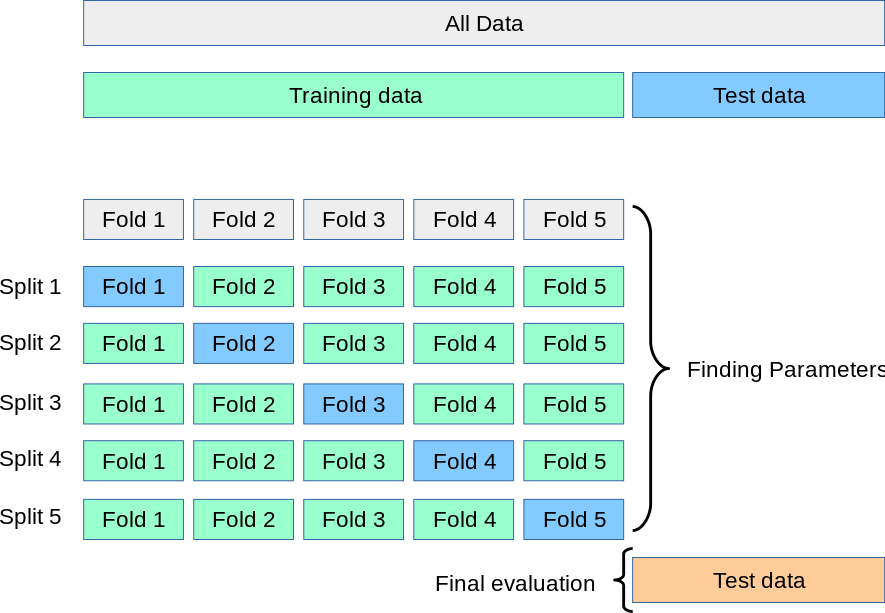
Решение этой проблемы — процедура, называемая кросс-валидация (сокращенно CV). Тестовый набор все еще должен быть выделен для окончательной оценки, но валидационный набор больше не нужен при использовании CV. В базовом подходе, называемом k-кратной перекрестной проверки, обучающая выборка разбивается на k меньшие множества (другие подходы описаны ниже, но в целом следуют тем же принципам). Следующая процедура выполняется для каждого из k “folds”:

• Модель обучается с использованием \(k-1\) складок в качестве обучающих данных;

• полученная модель проверяется на оставшейся части данных (т.е. используется в качестве тестового набора для вычисления показателя производительности, такого как точность).

Мера производительности, сообщаемая k-кратная перекрестная проверка затем является средним значений, вычисленных в цикле. Этот подход может быть вычислительно затратным, но не тратит слишком много данных (как в случае фиксации произвольного проверочного набора), что является основным преимуществом в задачах, таких как обратный вывод, где количество выборок очень мало.

3.1.1. Вычисление перекрёстно-валидированных метрик

Самый простой способ использования перекрестной проверки — вызвать cross_val_score вспомогательная функция на оценщике и наборе данных.

Следующий пример демонстрирует, как оценить точность линейного ядерного метода опорных векторов на наборе данных ирисов, разделяя данные, обучая модель и вычисляя оценку 5 раз подряд (с разными разделениями каждый раз):

>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1, random_state=42)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores
array([0.96, 1. , 0.96, 0.96, 1. ])

Средний балл и стандартное отклонение, следовательно, даются:

>>> print("%0.2f accuracy with a standard deviation of %0.2f" % (scores.mean(), scores.std()))
0.98 accuracy with a standard deviation of 0.02

По умолчанию оценка, вычисляемая на каждой итерации CV, является score метод оценщика. Это можно изменить, используя параметр оценки:

>>> from sklearn import metrics
>>> scores = cross_val_score(
...     clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96, 1., 0.96, 0.96, 1.])

См. Параметр scoring: определение правил оценки модели для подробностей. В случае набора данных Iris выборки сбалансированы по целевым классам, поэтому точность и F1-оценка почти равны.

Когда cv аргумент является целым числом, cross_val_score использует KFold или StratifiedKFold стратегии по умолчанию, последняя используется, если оценщик наследуется от ClassifierMixin.

Также возможно использовать другие стратегии перекрестной проверки, передавая итератор перекрестной проверки, например:

>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977, 0.977, 1., 0.955, 1.])

Другой вариант — использовать итерируемый объект, возвращающий (обучающие, тестовые) разбиения в виде массивов индексов, например:

>>> def custom_cv_2folds(X):
...     n = X.shape[0]
...     i = 1
...     while i <= 2:
...         idx = np.arange(n * (i - 1) / 2, n * i / 2, dtype=int)
...         yield idx, idx
...         i += 1
...
>>> custom_cv = custom_cv_2folds(X)
>>> cross_val_score(clf, X, y, cv=custom_cv)
array([1.        , 0.973])

Преобразование данных с удержанными данными

Так же, как важно тестировать предсказатель на данных, исключённых из обучения, предобработка (такая как стандартизация, выбор признаков и т.д.) и аналогичные преобразования данных аналогично должно быть изучено на обучающем наборе и применено к отложенным данным для предсказания:

>>> from sklearn import preprocessing
>>> X_train, X_test, y_train, y_test = train_test_split(
...     X, y, test_size=0.4, random_state=0)
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> X_train_transformed = scaler.transform(X_train)
>>> clf = svm.SVC(C=1).fit(X_train_transformed, y_train)
>>> X_test_transformed = scaler.transform(X_test)
>>> clf.score(X_test_transformed, y_test)
0.9333

A Pipeline облегчает компоновку оценщиков, обеспечивая это поведение при перекрестной проверке:

>>> from sklearn.pipeline import make_pipeline
>>> clf = make_pipeline(preprocessing.StandardScaler(), svm.SVC(C=1))
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977, 0.933, 0.955, 0.933, 0.977])

См. Конвейеры и составные оценщики.

3.1.1.1. Функция cross_validate и оценка нескольких метрик

The cross_validate функция отличается от cross_val_score двумя способами:

• Он позволяет указывать несколько метрик для оценки.

• Возвращает словарь, содержащий времена обучения, времена оценки (и, опционально, оценки обучения, обученные оценщики, индексы разделения на обучающую и тестовую выборки) в дополнение к тестовой оценке.

Для оценки по одной метрике, где параметр scoring является строкой, вызываемым объектом или None, ключи будут - ['test_score', 'fit_time', 'score_time']

А для оценки по нескольким метрикам возвращаемое значение — это словарь со следующими ключами - ['test_', 'test_', 'test_', 'fit_time', 'score_time']

return_train_score установлено в False по умолчанию для экономии времени вычислений. Чтобы оценить результаты на обучающем наборе, вам нужно установить его в True. Вы также можете сохранить оценщик, обученный на каждом обучающем наборе, установив return_estimator=True. Аналогично, вы можете установить return_indices=True для сохранения индексов обучающей и тестовой выборок, используемых для разделения набора данных на обучающую и тестовую выборки для каждого разбиения cv.

Несколько метрик могут быть указаны либо как список, кортеж или набор предопределенных имен оценщиков:

>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96, 1., 0.96, 0.96, 1.])

Или как словарь, сопоставляющий имя скорера с предопределенной или пользовательской функцией оценки:

>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
...            'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
...                         cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
 'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
array([0.97, 0.97, 0.99, 0.98, 0.98])

Вот пример cross_validate используя одну метрику:

>>> scores = cross_validate(clf, X, y,
...                         scoring='precision_macro', cv=5,
...                         return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']

3.1.1.2. Получение прогнозов с помощью перекрестной проверки

Функция cross_val_predict имеет похожий интерфейс на cross_val_score, но возвращает для каждого элемента входных данных прогноз, который был получен для этого элемента, когда он находился в тестовом наборе. Можно использовать только стратегии перекрестной проверки, которые назначают все элементы тестовому набору ровно один раз (в противном случае возникает исключение).

Предупреждение

Примечание о неправильном использовании cross_val_predict

Результат cross_val_predict может отличаться от полученных с использованием cross_val_score поскольку элементы сгруппированы разными способами. Функция cross_val_score берёт среднее по фолдам кросс-валидации, тогда как cross_val_predict просто возвращает метки (или вероятности) из нескольких различных моделей без различия. Таким образом, cross_val_predict не является подходящей мерой ошибки обобщения.

Функция cross_val_predict подходит для:

• Визуализация предсказаний, полученных от различных моделей.

• Смешивание моделей: Когда предсказания одного контролируемого оценивателя используются для обучения другого оценивателя в ансамблевых методах.

Доступные итераторы перекрестной проверки представлены в следующем разделе.

Примеры

• Рабочая характеристика приёмника (ROC) с перекрёстной проверкой,

• Рекурсивное исключение признаков с перекрестной проверкой,

• Пользовательская стратегия повторного обучения для поиска по сетке с кросс-валидацией,

• Примерный пайплайн для извлечения и оценки текстовых признаков,

• Построение перекрестно проверенных предсказаний,

• Вложенная и невложенная перекрестная проверка.

3.1.2. Итераторы перекрестной проверки

Следующие разделы перечисляют утилиты для генерации индексов, которые можно использовать для создания разбиений набора данных в соответствии с различными стратегиями перекрестной проверки.

3.1.2.1. Итераторы перекрестной проверки для независимых и одинаково распределенных данных

Предположение, что некоторые данные независимы и одинаково распределены (i.i.d.), означает, что все выборки происходят из одного и того же генеративного процесса, и предполагается, что генеративный процесс не имеет памяти о прошлых сгенерированных выборках.

Следующие перекрестные валидаторы могут быть использованы в таких случаях.

Примечание

Хотя независимые и одинаково распределенные данные — распространенное предположение в теории машинного обучения, на практике оно редко выполняется. Если известно, что образцы были сгенерированы с использованием зависящего от времени процесса, безопаснее использовать схема перекрестной проверки с учетом временных рядов. Аналогично, если мы знаем, что генеративный процесс имеет групповую структуру (образцы собраны от разных субъектов, экспериментов, измерительных устройств), безопаснее использовать кросс-валидация по группам.

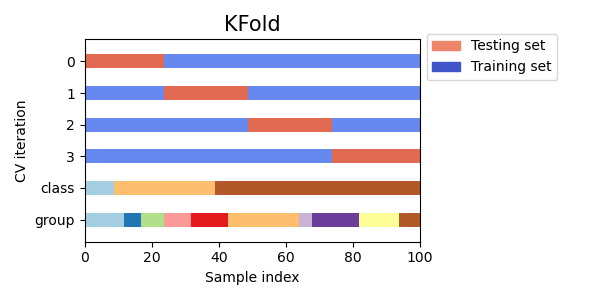
3.1.2.1.1. K-fold

KFold разделяет все образцы в \(k\) группы образцов, называемые фолдами (если \(k = n\), это эквивалентно Leave One Out стратегии), одинакового размера (если возможно). Функция предсказания обучается с использованием \(k - 1\) сгибов, и оставленный сгиб используется для тестирования.

Пример 2-кратной перекрестной проверки на наборе данных с 4 выборками:

>>> import numpy as np
>>> from sklearn.model_selection import KFold

>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]

Вот визуализация поведения перекрестной проверки. Обратите внимание, что KFold не зависит от классов или групп.

Каждый фолд состоит из двух массивов: первый связан с обучающая выборка, а второй к тестовый набор. Таким образом, можно создать обучающие/тестовые наборы с использованием индексации numpy:

>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> y = np.array([0, 1, 0, 1])
>>> X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]

3.1.2.1.2. Повторяемая K-кратная перекрестная проверка

RepeatedKFold повторы KFold \(n\) раз, создавая разные разбиения в каждом повторении.

Пример 2-кратного K-Fold, повторённого 2 раза:

>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
...     print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]

Аналогично, RepeatedStratifiedKFold повторы StratifiedKFold \(n\) раз с различной рандомизацией в каждом повторении.

3.1.2.1.3. Метод исключения одного наблюдения (LOO)

LeaveOneOut (или LOO) - это простая кросс-валидация. Каждый обучающий набор создается путем взятия всех образцов, кроме одного, тестовый набор - это оставленный образец. Таким образом, для \(n\) образцов, у нас есть \(n\) различные обучающие наборы и \(n\) различных тестовых наборов. Эта процедура кросс-валидации не тратит много данных, так как только один образец удаляется из обучающего набора:

>>> from sklearn.model_selection import LeaveOneOut

>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
...     print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]

Потенциальным пользователям LOO для выбора модели следует учитывать несколько известных предостережений. По сравнению с \(k\)-кратная перекрёстная проверка, один строит \(n\) модели из \(n\) выборок вместо \(k\) модели, где \(n > k\). Более того, каждый обучается на \(n - 1\) образцы, а не \((k-1) n / k\). В обоих случаях, предполагая \(k\) не слишком велико и \(k < n\), LOO требует больше вычислительных ресурсов, чем \(k\)-кратная перекрестная проверка.

С точки зрения точности, LOO часто приводит к высокой дисперсии как оценщик для ошибки тестирования. Интуитивно, поскольку \(n - 1\) из \(n\) образцы используются для построения каждой модели, модели, построенные на фолдах, практически идентичны друг другу и модели, построенной на всем обучающем наборе.

Однако, если кривая обучения крутая для рассматриваемого размера обучающей выборки, то 5- или 10-кратная перекрестная проверка может переоценить ошибку обобщения.

Как общее правило, большинство авторов и эмпирические данные свидетельствуют о том, что 5- или 10-кратная перекрестная проверка должна быть предпочтительнее LOO.

Ссылки

• http://www.faqs.org/faqs/ai-faq/neural-nets/part3/section-12.html;

• T. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer 2009

• L. Breiman, P. Spector Выбор и оценка подмодели в регрессии: случай X-случайный, International Statistical Review 1992;

• R. Kohavi, Исследование перекрестной проверки и бутстрапа для оценки точности и выбора модели, Intl. Jnt. Conf. AI

• R. Bharat Rao, G. Fung, R. Rosales, Об опасностях кросс-валидации. Экспериментальная оценка, SIAM 2008;

• G. James, D. Witten, T. Hastie, R. Tibshirani, An Introduction to Statistical Learning, Springer 2013.

3.1.2.1.4. Leave P Out (LPO)

LeavePOut очень похож на LeaveOneOut так как он создает все возможные обучающие/тестовые наборы, удаляя \(p\) выборки из полного набора. Для \(n\) образцы, это создает \({n \choose p}\) пары обучающая-тестовая. В отличие от LeaveOneOut и KFold, тестовые наборы будут перекрываться для \(p > 1\).

Пример Leave-2-Out на наборе данных с 4 выборками:

>>> from sklearn.model_selection import LeavePOut

>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
...     print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]

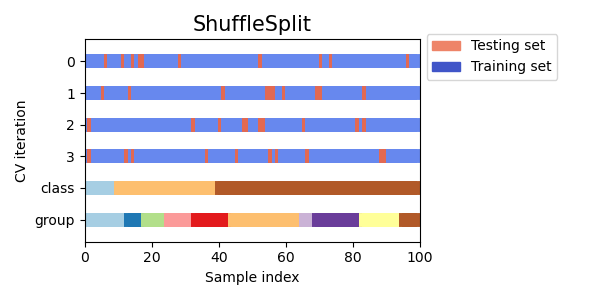
3.1.2.1.5. Перекрёстная проверка со случайными перестановками, также известная как Shuffle & Split

The ShuffleSplit итератор будет генерировать определенное пользователем количество независимых разделений на обучающий и тестовый наборы данных. Сначала образцы перемешиваются, а затем разбиваются на пары обучающих и тестовых наборов.

Можно управлять случайностью для воспроизводимости результатов, явно задавая seed для random_state псевдослучайного генератора чисел.

Вот пример использования:

>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.arange(10)
>>> ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
>>> for train_index, test_index in ss.split(X):
...     print("%s %s" % (train_index, test_index))
[9 1 6 7 3 0 5] [2 8 4]
[2 9 8 0 6 7 4] [3 5 1]
[4 5 1 0 6 9 7] [2 3 8]
[2 7 5 8 0 3 4] [6 1 9]
[4 1 0 6 8 9 3] [5 2 7]

Вот визуализация поведения перекрестной проверки. Обратите внимание, что ShuffleSplit не зависит от классов или групп.

ShuffleSplit является хорошей альтернативой KFold перекрестная валидация, которая позволяет более тонко контролировать количество итераций и долю выборок с каждой стороны разделения на обучающую/тестовую выборки.

3.1.2.2. Итераторы перекрестной проверки со стратификацией на основе меток классов

Некоторые задачи классификации могут естественным образом содержать редкие классы: например, может быть на порядки больше отрицательных наблюдений, чем положительных (например, медицинский скрининг, обнаружение мошенничества и т.д.). В результате разбиение кросс-валидации может создавать обучающие или валидационные фолды без единого вхождения определённого класса. Это обычно приводит к неопределённым метрикам классификации (например, ROC AUC), исключениям при попытке вызвать fit или отсутствующие столбцы в выводе predict_proba или decision_function методы многоклассовых классификаторов, обученных на разных сгибах.

Для смягчения таких проблем сплиттеры, такие как StratifiedKFold и StratifiedShuffleSplit реализовать стратифицированную выборку, чтобы обеспечить приблизительное сохранение относительных частот классов в каждом сгибе.

Примечание

Стратифицированная выборка была введена в scikit-learn для обхода упомянутых инженерных проблем, а не для решения статистической.

Стратификация делает складки перекрестной проверки более однородными, и в результате скрывает часть изменчивости, присущей подгонке моделей с ограниченным количеством наблюдений.

В результате стратификация может искусственно уменьшить разброс метрики, измеренной по итерациям кросс-валидации: межфолдная изменчивость больше не отражает неопределенность в производительности классификаторов при наличии редких классов.

3.1.2.2.1. Стратифицированная K-кратная

StratifiedKFold является вариацией K-fold который возвращает стратифицированный фолды: каждый набор содержит примерно одинаковый процент образцов каждого целевого класса, как и полный набор.

Вот пример стратифицированной 3-кратной перекрестной проверки на наборе данных с 50 образцами из двух несбалансированных классов. Мы показываем количество образцов в каждом классе и сравниваем с KFold.

>>> from sklearn.model_selection import StratifiedKFold, KFold
>>> import numpy as np
>>> X, y = np.ones((50, 1)), np.hstack(([0] * 45, [1] * 5))
>>> skf = StratifiedKFold(n_splits=3)
>>> for train, test in skf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [30  3]   |   test -  [15  2]
train -  [30  3]   |   test -  [15  2]
train -  [30  4]   |   test -  [15  1]
>>> kf = KFold(n_splits=3)
>>> for train, test in kf.split(X, y):
...     print('train -  {}   |   test -  {}'.format(
...         np.bincount(y[train]), np.bincount(y[test])))
train -  [28  5]   |   test -  [17]
train -  [28  5]   |   test -  [17]
train -  [34]   |   test -  [11  5]

Мы видим, что StratifiedKFold сохраняет соотношения классов (приблизительно 1/10) в обеих обучающей и тестовой выборках.

Вот визуализация поведения перекрёстной проверки.

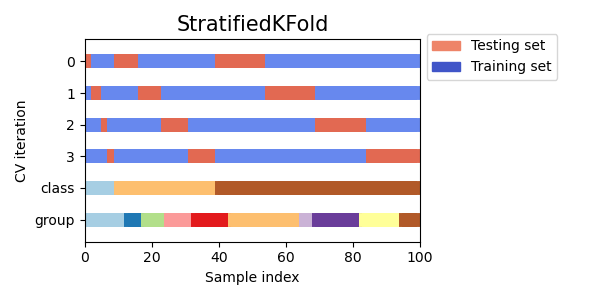
RepeatedStratifiedKFold может использоваться для повторения Стратифицированной K-Блочной выборки n раз с различной рандомизацией в каждом повторении.

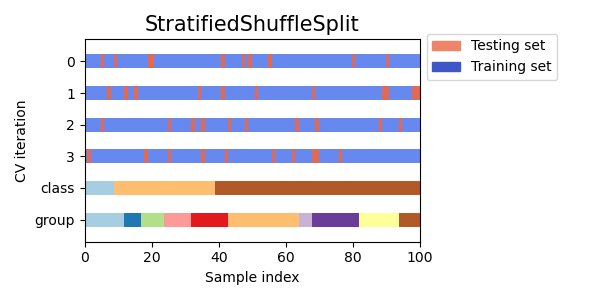
3.1.2.2.2. Стратифицированное случайное разбиение

StratifiedShuffleSplit является вариацией ShuffleSplit, которая возвращает стратифицированные разбиения, т.е. которая создает разделения, сохраняя тот же процент для каждого целевого класса, как и в полном наборе.

Вот визуализация поведения перекрёстной проверки.

3.1.2.3. Предопределенные разделения сгибов / Валидационные наборы

Для некоторых наборов данных уже существует предопределенное разделение данных на обучающую и проверочную выборки или на несколько перекрестных проверочных фолдов. Используя PredefinedSplit можно использовать эти фолды, например, при поиске гиперпараметров.

Например, при использовании валидационного набора, установите test_fold в 0 для всех образцов, которые являются частью проверочного набора, и в -1 для всех остальных образцов.

3.1.2.4. Итераторы перекрестной проверки для сгруппированных данных

Предположение о независимости и одинаковой распределенности нарушается, если базовый генеративный процесс создаёт группы зависимых выборок.

Такая группировка данных зависит от предметной области. Примером может быть медицинские данные, собранные от нескольких пациентов, с несколькими образцами, взятыми от каждого пациента. И такие данные, вероятно, зависят от индивидуальной группы. В нашем примере идентификатор пациента для каждого образца будет его групповым идентификатором.

В этом случае мы хотели бы знать, обобщает ли модель, обученная на определенном наборе групп, хорошо на невидимые группы. Чтобы измерить это, нам нужно убедиться, что все образцы в проверочной выборке происходят из групп, которые совсем не представлены в парной обучающей выборке.

Следующие разделители перекрестной проверки могут быть использованы для этого. Идентификатор группировки для выборок указывается через groups параметр.

3.1.2.4.1. Групповая K-блочная выборка

GroupKFold является вариацией K-fold, которая гарантирует, что одна и та же группа не представлена в тестовых и обучающих наборах одновременно. Например, если данные получены от разных субъектов с несколькими образцами на субъекта и если модель достаточно гибкая, чтобы учиться на сильно персонализированных признаках, она может не обобщиться на новых субъектов. GroupKFold позволяет обнаруживать такие ситуации переобучения.

Представьте, что у вас есть три субъекта, каждый с ассоциированным числом от 1 до 3:

>>> from sklearn.model_selection import GroupKFold

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
>>> groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

>>> gkf = GroupKFold(n_splits=3)
>>> for train, test in gkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]

Каждый субъект находится в отдельном тестовом фолде, и один и тот же субъект никогда не находится одновременно в тестовой и обучающей выборках. Обратите внимание, что фолды не имеют точно одинакового размера из-за дисбаланса в данных. Если пропорции классов должны быть сбалансированы по фолдам, StratifiedGroupKFold является лучшим вариантом.

Вот визуализация поведения перекрёстной проверки.

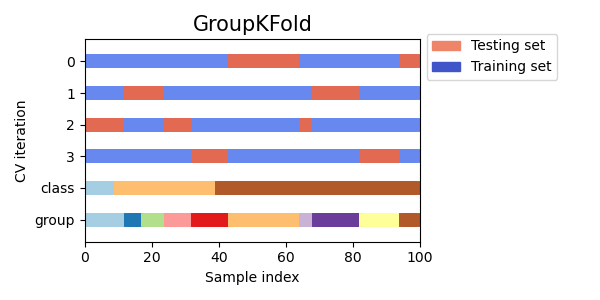
Аналогично KFold, тестовые наборы из GroupKFold сформирует полное разделение всех данных.

В то время как GroupKFold пытается разместить одинаковое количество образцов в каждой свертке, когда shuffle=False, когда shuffle=True он пытается разместить равное количество различных групп в каждой фолде (но не учитывает размеры групп).

3.1.2.4.2. StratifiedGroupKFold

StratifiedGroupKFold — это схема перекрестной проверки, которая объединяет как StratifiedKFold и GroupKFold. Идея заключается в попытке сохранить распределение классов в каждом разбиении, сохраняя каждую группу в одном разбиении. Это может быть полезно, когда у вас несбалансированный набор данных, так что использование только GroupKFold может привести к смещенным разбиениям.

Пример:

>>> from sklearn.model_selection import StratifiedGroupKFold
>>> X = list(range(18))
>>> y = [1] * 6 + [0] * 12
>>> groups = [1, 2, 3, 3, 4, 4, 1, 1, 2, 2, 3, 4, 5, 5, 5, 6, 6, 6]
>>> sgkf = StratifiedGroupKFold(n_splits=3)
>>> for train, test in sgkf.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[ 0  2  3  4  5  6  7 10 11 15 16 17] [ 1  8  9 12 13 14]
[ 0  1  4  5  6  7  8  9 11 12 13 14] [ 2  3 10 15 16 17]
[ 1  2  3  8  9 10 12 13 14 15 16 17] [ 0  4  5  6  7 11]

00:05.164

• При текущей реализации полное перемешивание невозможно в большинстве сценариев. Когда shuffle=True, происходит следующее:

  1. Все группы перемешиваются.

  2. Группы сортируются по стандартному отклонению классов с использованием устойчивой сортировки.

  3. Отсортированные группы перебираются и назначаются фолдам.

  Это означает, что только группы с одинаковым стандартным отклонением распределения классов будут перемешаны, что может быть полезно, когда каждая группа содержит только один класс.

• Алгоритм жадным образом назначает каждую группу одному из n_splits тестовых наборов, выбирая тестовый набор, который минимизирует дисперсию в распределении классов по тестовым наборам. Назначение групп происходит от групп с наибольшей к наименьшей дисперсии в частоте классов, т.е. большие группы, сконцентрированные на одном или нескольких классах, назначаются первыми.

• Это разбиение неоптимально в том смысле, что оно может создавать несбалансированные разбиения, даже если возможна идеальная стратификация. Если у вас относительно близкое распределение классов в каждой группе, используя GroupKFold лучше.

Вот визуализация поведения перекрестной проверки для неравномерных групп:

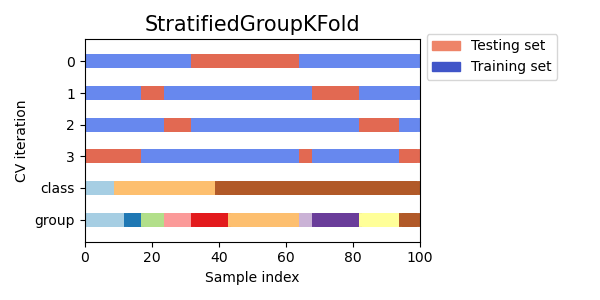
3.1.2.4.3. Leave One Group Out

LeaveOneGroupOut является схемой перекрестной проверки, где каждое разделение исключает образцы, принадлежащие одной конкретной группе. Информация о группе предоставляется через массив, который кодирует группу каждого образца.

Каждый обучающий набор, таким образом, состоит из всех выборок, кроме тех, которые относятся к определённой группе. Это то же самое, что LeavePGroupsOut с n_groups=1 и то же самое, что GroupKFold с n_splits равно количеству уникальных меток, переданных в groups параметр.

Например, в случае множественных экспериментов, LeaveOneGroupOut может использоваться для создания перекрёстной проверки на основе различных экспериментов: мы создаём обучающий набор, используя выборки всех экспериментов, кроме одного:

>>> from sklearn.model_selection import LeaveOneGroupOut

>>> X = [1, 5, 10, 50, 60, 70, 80]
>>> y = [0, 1, 1, 2, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3, 3]
>>> logo = LeaveOneGroupOut()
>>> for train, test in logo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[2 3 4 5 6] [0 1]
[0 1 4 5 6] [2 3]
[0 1 2 3] [4 5 6]

Другое распространенное применение — использование информации о времени: например, группы могут быть годом сбора образцов и, таким образом, позволять кросс-валидацию по временным разбиениям.

3.1.2.4.4. Оставить P групп вне

LeavePGroupsOut похож на LeaveOneGroupOut, но удаляет выборки, связанные с \(P\) группы для каждого обучающего/тестового набора. Все возможные комбинации \(P\) группы исключаются, что означает, что тестовые наборы будут перекрываться для \(P>1\).

Пример Leave-2-Group Out:

>>> from sklearn.model_selection import LeavePGroupsOut

>>> X = np.arange(6)
>>> y = [1, 1, 1, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3]
>>> lpgo = LeavePGroupsOut(n_groups=2)
>>> for train, test in lpgo.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]

3.1.2.4.5. Group Shuffle Split

The GroupShuffleSplit итератор ведёт себя как комбинация ShuffleSplit и LeavePGroupsOutи генерирует последовательность рандомизированных разбиений, в которых подмножество групп исключается для каждого разделения. Каждое разделение на обучающую и тестовую выборки выполняется независимо, что означает отсутствие гарантированной связи между последовательными тестовыми наборами.

Вот пример использования:

>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "a"]
>>> groups = [1, 1, 2, 2, 3, 3, 4, 4]
>>> gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
>>> for train, test in gss.split(X, y, groups=groups):
...     print("%s %s" % (train, test))
...
[0 1 2 3] [4 5 6 7]
[2 3 6 7] [0 1 4 5]
[2 3 4 5] [0 1 6 7]
[4 5 6 7] [0 1 2 3]

Вот визуализация поведения перекрёстной проверки.

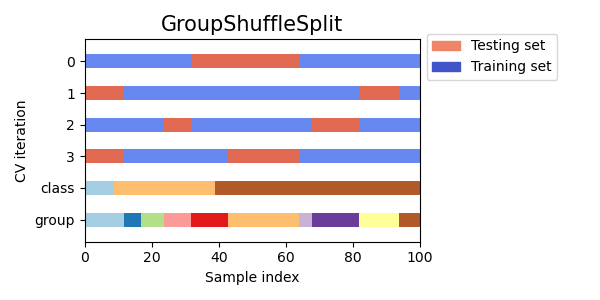
Этот класс полезен, когда поведение LeavePGroupsOut желательно, но количество групп достаточно велико, чтобы генерировать все возможные разбиения с \(P\) исключенные группы были бы непомерно дороги. В таком сценарии, GroupShuffleSplit предоставляет случайную выборку (с возвращением) разделений на обучающую/тестовую выборки, сгенерированных LeavePGroupsOut.

3.1.2.5. Использование итераторов перекрестной проверки для разделения на обучающую и тестовую выборки

Вышеуказанные функции перекрёстной проверки по группам также могут быть полезны для разделения набора данных на обучающую и тестовую подвыборки. Обратите внимание, что удобная функция train_test_split является оберткой вокруг ShuffleSplit и поэтому позволяет только стратифицированное разделение (с использованием меток классов) и не может учитывать группы.

Чтобы выполнить разделение на обучающую и тестовую выборки, используйте индексы для обучающей и тестовой подвыборок, полученные генератором, выводимым split() метод разделителя перекрестной проверки. Например:

>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit

>>> X = np.array([0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001])
>>> y = np.array(["a", "b", "b", "b", "c", "c", "c", "a"])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 4, 4])
>>> train_indx, test_indx = next(
...     GroupShuffleSplit(random_state=7).split(X, y, groups)
... )
>>> X_train, X_test, y_train, y_test = \
...     X[train_indx], X[test_indx], y[train_indx], y[test_indx]
>>> X_train.shape, X_test.shape
((6,), (2,))
>>> np.unique(groups[train_indx]), np.unique(groups[test_indx])
(array([1, 2, 4]), array([3]))

3.1.2.6. Перекрёстная проверка данных временных рядов

Данные временных рядов характеризуются корреляцией между наблюдениями, близкими по времени (автокорреляция). Однако классические техники перекрестной проверки, такие как KFold и ShuffleSplit предполагают, что выборки независимы и одинаково распределены, что приведет к необоснованной корреляции между обучающими и тестовыми экземплярами (давая плохие оценки ошибки обобщения) на данных временных рядов. Поэтому очень важно оценивать нашу модель для данных временных рядов на "будущих" наблюдениях, наименее похожих на те, которые использовались для обучения модели. Для достижения этого одно решение предоставляется TimeSeriesSplit.

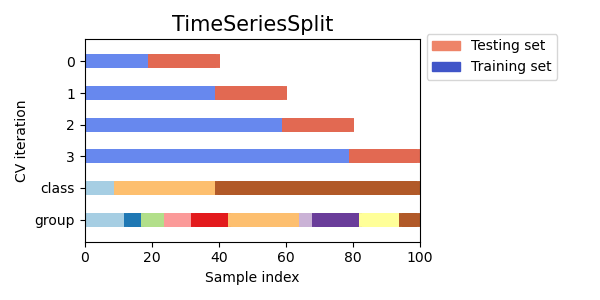
3.1.2.6.1. Разделение временных рядов

TimeSeriesSplit является вариацией k-кратная который возвращает сначала \(k\) сгибы как обучающий набор и \((k+1)\) th-я выборка в качестве тестового набора. Обратите внимание, что в отличие от стандартных методов перекрестной проверки, последовательные обучающие наборы являются надмножествами предыдущих. Кроме того, все избыточные данные добавляются к первому обучающему разделу, который всегда используется для обучения модели.

Этот класс может использоваться для перекрестной проверки временных рядов, наблюдаемых с фиксированными временными интервалами. Действительно, фолды должны представлять одинаковую продолжительность, чтобы иметь сопоставимые метрики между фолдами.

Пример 3-раздельной перекрестной проверки временных рядов на наборе данных с 6 образцами:

>>> from sklearn.model_selection import TimeSeriesSplit

>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit(n_splits=3)
>>> print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
>>> for train, test in tscv.split(X):
...     print("%s %s" % (train, test))
[0 1 2] [3]
[0 1 2 3] [4]
[0 1 2 3 4] [5]

Вот визуализация поведения перекрёстной проверки.

3.1.3. Замечание о перемешивании

Если порядок данных не произвольный (например, образцы с одинаковой меткой класса идут подряд), их перемешивание сначала может быть важно для получения значимого результата перекрестной проверки. Однако обратное может быть верно, если образцы не являются независимыми и одинаково распределенными. Например, если образцы соответствуют новостным статьям и упорядочены по времени публикации, то перемешивание данных, вероятно, приведет к переобученной модели и завышенной оценке валидации: она будет тестироваться на образцах, искусственно похожих (близких по времени) на обучающие образцы.

Некоторые итераторы перекрестной проверки, такие как KFold, имеют встроенную опцию перемешивания индексов данных перед их разделением. Обратите внимание, что:

• Это потребляет меньше памяти, чем непосредственное перемешивание данных.

• По умолчанию перемешивание не происходит, включая (стратифицированную) K-кратную перекрёстную проверку, выполняемую указанием cv=some_integer to cross_val_score, поиск по сетке и т.д. Помните, что train_test_split всё равно возвращает случайное разделение.

• The random_state параметр по умолчанию равен None, что означает, что перемешивание будет разным каждый раз KFold(..., shuffle=True) итерируется. Однако, GridSearchCV будет использовать одинаковое перемешивание для каждого набора параметров, проверяемых одним вызовом его fit метод.

• Чтобы получить идентичные результаты для каждого разбиения, установите random_state в целое число.

Для более подробной информации о том, как контролировать случайность разделителей cv и избегать распространенных ошибок, см. Управление случайностью.

3.1.4. Перекрестная проверка и выбор модели

Итераторы перекрестной проверки также могут использоваться для непосредственного выполнения выбора модели с помощью Grid Search для оптимальных гиперпараметров модели. Это тема следующего раздела: Настройка гиперпараметров оценщика.

3.1.5. Оценка перестановочного теста

permutation_test_score {‘percentile’, ‘k_best’, ‘fpr’, ‘fdr’, ‘fwe’}, по умолчанию=’percentile’ предиктораОн предоставляет p-значение на основе перестановок, которое показывает, насколько вероятно, что наблюдаемая производительность оценщика была получена случайно. Нулевая гипотеза в этом тесте заключается в том, что оценщик не использует никакую статистическую зависимость между признаками и целевыми переменными для правильного прогнозирования на отложенных данных. permutation_test_score генерирует нулевое распределение, вычисляя n_permutations различных перестановок данных. В каждой перестановке значения целевой переменной случайным образом перемешиваются, тем самым удаляя любую зависимость между признаками и целями. Выводимое p-значение - это доля перестановок, чья оценка перекрестной проверки лучше или равна истинной оценке без перестановки целей. Для надежных результатов n_permutations обычно должен быть больше 100 и cv от 3 до 10 фолдов.

Низкое p-значение предоставляет доказательства того, что набор данных содержит реальную зависимость между признаками и целевыми переменными и что оценщик смог использовать эту зависимость для получения хороших результатов. Высокое p-значение, наоборот, может быть вызвано одной из этих причин:

• отсутствие зависимости между признаками и целевыми переменными (т.е. нет систематической связи, и любые наблюдаемые закономерности, вероятно, случайны)

• или потому что оценщик не смог использовать зависимость в данных (например, из-за недообучения).

В последнем случае использование более подходящего оценщика, способного использовать структуру в данных, приведет к более низкому p-значению.

Перекрёстная проверка предоставляет информацию о том, насколько хорошо оценщик обобщает, оценивая диапазон его ожидаемых оценок. Однако оценщик, обученный на многомерном наборе данных без структуры, всё равно может работать лучше, чем ожидалось, при перекрёстной проверке, просто случайно. Это обычно может происходить с небольшими наборами данных, содержащими менее нескольких сотен образцов. permutation_test_score предоставляет информацию о том, обнаружил ли оценщик реальную зависимость между признаками и целями, и может помочь в оценке производительности оценщика.

Важно отметить, что этот тест, как было показано, дает низкие p-значения даже если в данных есть только слабая структура, потому что в соответствующих перемешанных наборах данных нет абсолютно никакой структуры. Этот тест поэтому способен только показать, надежно ли модель превосходит случайное угадывание.

Наконец, permutation_test_score вычисляется методом грубой силы и внутренне обучает (n_permutations + 1) * n_cv моделей. Поэтому это осуществимо только с небольшими наборами данных, для которых обучение отдельной модели очень быстро. Используя n_jobs параметр распараллеливает вычисления и тем самым ускоряет их.

Примеры

• Тест с перестановками для значимости оценки классификации

Ссылки

• Ojala и Garriga. Перестановочные тесты для изучения производительности классификатора. J. Mach. Learn. Res. 2010.