3.4. Метрики и оценка: количественное измерение качества прогнозов

3.4.1. Какую функцию оценки мне следует использовать?

Прежде чем мы подробнее рассмотрим детали множества оценок и метрики оценки, мы хотим дать некоторые рекомендации, вдохновлённые статистической теорией принятия решений, по выбору функции оценки для контролируемое обучение, см. [Gneiting2009]:

• Какую функцию оценки мне следует использовать?

• Какая функция оценки подходит для моей задачи?

Вкратце, если задана функция оценки, например, в соревновании Kaggle или в бизнес-контексте, используйте её. Если вы свободны в выборе, начните с рассмотрения конечной цели и применения предсказания. Полезно различать два шага:

• Предсказание

• Принятие решений

Прогнозирование: Обычно зависимая переменная \(Y\) является случайной величиной, в том смысле, что существует не детерминированный функция \(Y = g(X)\) признаков \(X\). Вместо этого существует вероятностное распределение \(F\) of \(Y\). Можно стремиться предсказать все распределение, известное как вероятностное предсказание, или—что более важно для scikit-learn—создать точечный прогноз (или точечный прогноз) путем выбора свойства или функционала этого распределения \(F\). Типичными примерами являются среднее значение (математическое ожидание), медиана или квантиль переменной отклика \(Y\) (условно при \(X\)).

После того как это установлено, используйте строго согласованный функция оценки для этого (целевого) функционала, см. [Gneiting2009]. Это означает использование функции оценки, которая соответствует измерение расстояния между предсказаниями y_pred и истинную целевую функцию, используя наблюдения \(Y\), т.е. y_trueДля классификации строго правильных оценочных правил, см. Запись в Википедии для правила оценки и [Gneiting2007], совпадают со строго согласованными оценочными функциями. Таблица ниже предоставляет примеры. Можно сказать, что согласованные оценочные функции действуют как сыворотка правды в том, что они гарантируют “что правдивость […] является оптимальной стратегией в ожидании” [Gneiting2014].

После выбора строго согласованной функции оценки, её лучше использовать для обоих: как функцию потерь для обучения модели и как метрику/оценку при оценке модели и сравнении моделей.

Обратите внимание, что для регрессоров предсказание выполняется с помощью predict в то время как для классификаторов это обычно predict_proba.

Принятие решений: Наиболее распространенные решения принимаются в задачах бинарной классификации, где результат predict_proba превращается в единый исход, например, из предсказанной вероятности дождя принимается решение о том, как действовать (принимать ли меры предосторожности, такие как зонт, или нет). Для классификаторов это то, что predict возвращает. См. также Настройка порога принятия решения для предсказания класса. Существует множество оценочных функций, которые измеряют различные аспекты такого решения, большинство из них охвачены или выведены из metrics.confusion_matrix.

Список строго согласованных функций оценки: Здесь мы перечисляем некоторые из наиболее релевантных статистических функционалов и соответствующие строго согласованные функции оценки для практических задач. Обратите внимание, что список не является полным и их больше. Для дальнейших критериев выбора конкретной см. [Fissler2022].

functional	функция оценки или потерь	ответ y	предсказание
Классификация
mean	Оценка Брайера 1	многоклассовый	predict_proba
mean	логарифмические потери	многоклассовый	predict_proba
mode	потеря zero-one 2	многоклассовый	predictкатегориальный
Регрессия
mean	квадратичная ошибка 3	все вещественные числа	predict, все вещественные числа
mean	Дисперсия Пуассона	неотрицательный	predict, строго положительный
mean	Гамма-девиация	строго положительные	predict, строго положительный
mean	804414	зависит от power	predict, зависит от power
медиана	абсолютная ошибка	все вещественные числа	predict, все вещественные числа
квантиль	потери пинболла	все вещественные числа	predict, все вещественные числа
mode	не существует согласованного	вещественные числа

¹ Оценка Брайера — это просто другое название для квадратичной ошибки в случае классификации с one-hot кодированными целевыми значениями.

² Zero-one loss является только согласованной, но не строго согласованной для моды. Zero-one loss эквивалентна единице минус accuracy score, что означает разные значения оценки, но тот же ранжинг.

³ R² дает тот же ранжинг, что и квадратичная ошибка.

Фиктивный пример: Сделаем приведенные выше аргументы более наглядными. Рассмотрим задачу в области надежности сетей, например, поддержание стабильного интернет- или Wi-Fi-соединения. Как провайдер сети, у вас есть доступ к набору данных логов сетевых соединений, содержащих нагрузку сети во времени и множество интересных признаков. Ваша цель — повысить надежность соединений. Фактически, вы обещаете клиентам, что как минимум в 99% всех дней не будет разрывов соединения длительностью более 1 минуты. Поэтому вас интересует прогноз 99% квантиля (наибольшей длительности разрыва соединения в день), чтобы заранее знать, когда добавить больше пропускной способности и тем самым удовлетворить клиентов. Таким образом, целевая функция является 99% квантилем. Из таблицы выше вы выбираете функцию потерь pinball в качестве функции оценки (справедливо, не так много выбора), для обучения модели (например, HistGradientBoostingRegressor(loss="quantile", quantile=0.99)) а также оценка модели (mean_pinball_loss(..., alpha=0.99) - приносим извинения за разные имена аргументов, quantile и alpha) будь то в поиске по сетке для нахождения гиперпараметров или в сравнении с другими моделями, такими как QuantileRegressor(quantile=0.99).

Ссылки

[Gneiting2007]

Т. Гнайтинг и А. Э. Рафтери. Строго Правильные Оценочные Правила, Прогнозирование и Оценка В: Journal of the American Statistical Association 102 (2007), стр. 359–378. ссылка на pdf

[Gneiting2009] (1,2)

T. Gneiting. Создание и оценка точечных прогнозов Journal of the American Statistical Association 106 (2009): 746 - 762.

[Gneiting2014]

T. Gneiting и M. Katzfuss. Вероятностное прогнозирование. В: Annual Review of Statistics and Its Application 1.1 (2014), стр. 125–151.

[Fissler2022]

T. Fissler, C. Lorentzen и M. Mayer. Сравнение моделей и оценка калибровки: руководство пользователя по согласованным функциям оценки в машинном обучении и актуарной практике.

3.4.2. Обзор API оценки

Существует 3 различных API для оценки качества предсказаний модели:

• Метод оценки оценщика: Оценщики имеют score метод, предоставляющий критерий оценки по умолчанию для решаемой проблемы. Чаще всего это точность для классификаторов и коэффициент детерминации (\(R^2\)) для регрессоров. Подробности для каждого оценщика можно найти в его документации.

• Параметр оценки: Инструменты оценки модели, которые используют кросс-валидация (такие как model_selection.GridSearchCV, model_selection.validation_curve и linear_model.LogisticRegressionCV) полагаются на внутренний оценка стратегия. Это можно указать с помощью scoring параметру этого инструмента и обсуждается в разделе Параметр scoring: определение правил оценки модели.

• Метрические функции: sklearn.metrics модуль реализует функции оценки ошибки предсказания для конкретных целей. Эти метрики подробно описаны в разделах о Метрики классификации, Метрики ранжирования для многометочной классификации, Метрики регрессии и Метрики кластеризации.

Наконец, Фиктивные оценки полезны для получения базового значения этих метрик для случайных предсказаний.

Смотрите также

Для "парных" метрик, между образцы а не оценщики или прогнозы, см. Парные метрики, сходства и ядра раздел.

3.4.3. The scoring параметр: определение правил оценки модели

Инструменты выбора и оценки модели, которые внутренне используют кросс-валидация (такие как model_selection.GridSearchCV, model_selection.validation_curve и linear_model.LogisticRegressionCV) принимают scoring параметр, который управляет тем, какую метрику они применяют к оцениваемым оценщикам.

Их можно указать несколькими способами:

• None: критерий оценки по умолчанию для оценщика (т.е., метрика, используемая в оценщике score метод) используется.

• String name: общие метрики могут передаваться через строковое имя.

• Callable: более сложные метрики могут быть переданы через пользовательский вызываемый объект метрики (например, функцию).

Некоторые инструменты также поддерживают множественную оценку метрик. См. Использование оценки по нескольким метрикам подробности.

3.4.3.1. Строковые имена скореров

Для наиболее распространенных случаев использования вы можете назначить объект оценки с помощью scoring параметр через строковое имя; таблица ниже показывает все возможные значения. Все объекты оценщиков следуют соглашению, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения. Таким образом, метрики, измеряющие расстояние между моделью и данными, такие как metrics.mean_squared_error, доступны как 'neg_mean_squared_error', которые возвращают отрицательное значение метрики.

Строковое название оценки	Функция	Комментарий
Классификация
‘accuracy’	metrics.accuracy_score
‘balanced_accuracy’	metrics.balanced_accuracy_score
‘top_k_accuracy’	metrics.top_k_accuracy_score
'average_precision'	metrics.average_precision_score
‘neg_brier_score’	metrics.brier_score_loss	требует predict_proba поддержка
'f1'	metrics.f1_score	для бинарных целей
'f1_micro'	metrics.f1_score	микроусреднённый
‘f1_macro’	metrics.f1_score	макроусредненный
'f1_weighted'	metrics.f1_score	взвешенное среднее
‘f1_samples’	metrics.f1_score	по многометочному образцу
'neg_log_loss'	metrics.log_loss	требует predict_proba поддержка
‘precision’ и т.д.	metrics.precision_score	суффиксы применяются как с 'f1'
‘recall’ и т.д.	metrics.recall_score	суффиксы применяются как с 'f1'
‘jaccard’ и т.д.	metrics.jaccard_score	суффиксы применяются как с 'f1'
'roc_auc'	metrics.roc_auc_score
‘roc_auc_ovr’	metrics.roc_auc_score
'roc_auc_ovo'	metrics.roc_auc_score
‘roc_auc_ovr_weighted’	metrics.roc_auc_score
‘roc_auc_ovo_weighted’	metrics.roc_auc_score
‘d2_log_loss_score’	metrics.d2_log_loss_score	требует predict_proba поддержка
‘d2_brier_score’	metrics.d2_brier_score	требует predict_proba поддержка
Кластеризация
‘adjusted_mutual_info_score’	metrics.adjusted_mutual_info_score
'adjusted_rand_score'	metrics.adjusted_rand_score
'completeness_score'	metrics.completeness_score
‘fowlkes_mallows_score’	metrics.fowlkes_mallows_score
'homogeneity_score'	metrics.homogeneity_score
‘mutual_info_score’	metrics.mutual_info_score
‘normalized_mutual_info_score’	metrics.normalized_mutual_info_score
'rand_score'	metrics.rand_score
'v_measure_score'	metrics.v_measure_score
Регрессия
'explained_variance'	metrics.explained_variance_score
'neg_max_error'	metrics.max_error
'neg_mean_absolute_error'	metrics.mean_absolute_error
‘neg_mean_squared_error’	metrics.mean_squared_error
‘neg_root_mean_squared_error’	metrics.root_mean_squared_error
‘neg_mean_squared_log_error’	metrics.mean_squared_log_error
‘neg_root_mean_squared_log_error’	metrics.root_mean_squared_log_error
‘neg_median_absolute_error’	metrics.median_absolute_error
‘r2’	metrics.r2_score
‘neg_mean_poisson_deviance’	metrics.mean_poisson_deviance
'neg_mean_gamma_deviance'	metrics.mean_gamma_deviance
‘neg_mean_absolute_percentage_error’	metrics.mean_absolute_percentage_error
‘d2_absolute_error_score’	metrics.d2_absolute_error_score

Примеры использования:

>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = svm.SVC(random_state=0)
>>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro')
array([0.96, 0.96, 0.96, 0.93, 1.        ])

Примечание

Если передано неправильное название метрики, возникает InvalidParameterError возникает исключение. Вы можете получить имена всех доступных оценщиков, вызвав get_scorer_names.

3.4.3.2. Вызываемые скореры

Для более сложных случаев использования и большей гибкости вы можете передать вызываемый объект в scoring параметр. Это можно сделать следующим образом:

• Адаптация предопределенных метрик через make_scorer

• Создание пользовательского объекта оценки (наиболее гибкий)

3.4.3.2.1. Адаптация предопределенных метрик через make_scorer

Следующие метрические функции не реализованы как именованные скореры, иногда потому что они требуют дополнительных параметров, таких как fbeta_score. Они не могут быть переданы в scoring параметры; вместо этого их вызываемый объект должен быть передан в make_scorer вместе со значением пользовательских параметров.

Функция	Параметр	Пример использования
Классификация
metrics.fbeta_score	beta	make_scorer(fbeta_score, beta=2)
Регрессия
metrics.mean_tweedie_deviance	power	make_scorer(mean_tweedie_deviance, power=1.5)
metrics.mean_pinball_loss	alpha	make_scorer(mean_pinball_loss, alpha=0.95)
metrics.d2_tweedie_score	power	make_scorer(d2_tweedie_score, power=1.5)
metrics.d2_pinball_score	alpha	make_scorer(d2_pinball_score, alpha=0.95)

Один типичный вариант использования — обернуть существующую метрическую функцию из библиотеки с нестандартными значениями ее параметров, такими как beta параметр для fbeta_score функция:

>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
...                     scoring=ftwo_scorer, cv=5)

Модуль sklearn.metrics также предоставляет набор простых функций для измерения ошибки предсказания при заданных истинных значениях и предсказаниях:

• функции, заканчивающиеся на _score возвращает значение для максимизации, чем выше, тем лучше.

• функции, заканчивающиеся на _error, _loss, или _deviance возвращает значение для минимизации, чем меньше, тем лучше. При преобразовании в объект оценки с помощью make_scorer, установите greater_is_better параметр для False (True по умолчанию; см. описание параметра ниже).

3.4.3.2.2. Создание пользовательского объекта оценки

Вы можете создать собственный объект оценки с помощью make_scorer.

Пользовательские объекты оценки с использованием make_scorer

Вы можете создать полностью пользовательский объект оценщика из простой python-функции, используя make_scorer, который может принимать несколько параметров:

• функцию Python, которую вы хотите использовать (my_custom_loss_func в примере ниже)

• возвращает ли функция Python оценку (greater_is_better=Trueпо умолчанию) или потерю (greater_is_better=False). Если это функция потерь, выход функции Python инвертируется объектом scorer, соответствуя конвенции кросс-валидации, что scorers возвращают более высокие значения для лучших моделей.

• только для метрик классификации: требует ли предоставленная вами функция Python непрерывных оценок уверенности решения. Если функция оценки принимает только вероятностные оценки (например, metrics.log_loss), то необходимо установить параметр response_method="predict_proba". Некоторые функции оценки не обязательно требуют оценок вероятности, а скорее не пороговых решающих значений (например, metrics.roc_auc_score). В этом случае можно предоставить список (например, response_method=["decision_function", "predict_proba"]), и скорер будет использовать первый доступный метод в порядке, указанном в списке, для вычисления оценок.

• любые дополнительные параметры функции оценки, такие как beta или labels.

Вот пример создания пользовательских скореров и использования greater_is_better параметр:

>>> import numpy as np
>>> def my_custom_loss_func(y_true, y_pred):
...     diff = np.abs(y_true - y_pred).max()
...     return float(np.log1p(diff))
...
>>> # score will negate the return value of my_custom_loss_func,
>>> # which will be np.log(2), 0.693, given the values for X
>>> # and y defined below.
>>> score = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> X = [[1], [1]]
>>> y = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(X, y)
>>> my_custom_loss_func(y, clf.predict(X))
0.69
>>> score(clf, X, y)
-0.69

Использование пользовательских оценщиков в функциях, где n_jobs > 1

Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкендом joblib по умолчанию (loky), импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкенда joblib.

Например, чтобы использовать n_jobs больше 1 в примере ниже, custom_scoring_function функция сохранена в созданном пользователем модуле (custom_scorer_module.py) и импортирован:

>>> from custom_scorer_module import custom_scoring_function
>>> cross_val_score(model,
...  X_train,
...  y_train,
...  scoring=make_scorer(custom_scoring_function, greater_is_better=False),
...  cv=5,
...  n_jobs=-1)

3.4.3.3. Использование оценки по нескольким метрикам

Scikit-learn также позволяет оценивать несколько метрик в GridSearchCV, RandomizedSearchCV и cross_validate.

Существует три способа указать несколько метрик оценки для scoring параметр:

• out-of-bag

  >>> scoring = ['accuracy', 'precision']
  

• Как dict сопоставляя имя оценщика с функцией оценки:

  >>> from sklearn.metrics import accuracy_score
  >>> from sklearn.metrics import make_scorer
  >>> scoring = {'accuracy': make_scorer(accuracy_score),
  ...            'prec': 'precision'}
  

  Обратите внимание, что значения словаря могут быть либо функциями оценки, либо одной из предопределенных метрических строк.

• Как вызываемый объект, возвращающий словарь оценок:

  >>> from sklearn.model_selection import cross_validate
  >>> from sklearn.metrics import confusion_matrix
  >>> # A sample toy binary classification dataset
  >>> X, y = datasets.make_classification(n_classes=2, random_state=0)
  >>> svm = LinearSVC(random_state=0)
  >>> def confusion_matrix_scorer(clf, X, y):
  ...      y_pred = clf.predict(X)
  ...      cm = confusion_matrix(y, y_pred)
  ...      return {'tn': cm[0, 0], 'fp': cm[0, 1],
  ...              'fn': cm[1, 0], 'tp': cm[1, 1]}
  >>> cv_results = cross_validate(svm, X, y, cv=5,
  ...                             scoring=confusion_matrix_scorer)
  >>> # Getting the test set true positive scores
  >>> print(cv_results['test_tp'])
  [10  9  8  7  8]
  >>> # Getting the test set false negative scores
  >>> print(cv_results['test_fn'])
  [0 1 2 3 2]
  

3.4.4. Метрики классификации

The sklearn.metrics модуль реализует несколько функций потерь, оценки и полезности для измерения производительности классификации. Некоторые метрики могут требовать оценок вероятности положительного класса, значений уверенности или двоичных решений. Большинство реализаций позволяют каждому образцу вносить взвешенный вклад в общую оценку через sample_weight параметр.

Некоторые из них ограничены случаем бинарной классификации:

precision_recall_curve(y_true, y_score, *[, ...])	Вычислите пары точность-полнота для различных порогов вероятности.
roc_curve(y_true, y_score, *[, pos_label, ...])	Вычислить характеристическую кривую оператора (ROC).
class_likelihood_ratios(y_true, y_pred, *[, ...])	Вычислить положительные и отрицательные отношения правдоподобия для бинарной классификации.
det_curve(y_true, y_score[, pos_label, ...])	Вычислите компромисс между ошибками обнаружения (DET) для различных порогов вероятности.
confusion_matrix_at_thresholds(y_true, y_score)	Вычислить бинарный термины матрицы ошибок для каждого порога классификации.

Другие также работают в многоклассовом случае:

balanced_accuracy_score(y_true, y_pred, *[, ...])	Вычисление сбалансированной точности.
cohen_kappa_score(y1, y2, *[, labels, ...])	Вычислить каппу Коэна: статистику, измеряющую согласие между аннотаторами.
confusion_matrix(y_true, y_pred, *[, ...])	Вычисление матрицы ошибок для оценки точности классификации.
hinge_loss(y_true, pred_decision, *[, ...])	Средняя потеря на шарнире (нерегуляризованная).
matthews_corrcoef(y_true, y_pred, *[, ...])	Вычислить коэффициент корреляции Мэттьюса (MCC).
roc_auc_score(y_true, y_score, *[, average, ...])	Вычисление площади под кривой рабочих характеристик приемника (ROC AUC) по прогнозным оценкам.
top_k_accuracy_score(y_true, y_score, *[, ...])	Оценка классификации по точности Top-k.

Некоторые также работают в случае мультиметок:

accuracy_score(y_true, y_pred, *[, ...])	Оценка точности классификации.
classification_report(y_true, y_pred, *[, ...])	Построить текстовый отчет, показывающий основные метрики классификации.
f1_score(y_true, y_pred, *[, labels, ...])	Вычислите оценку F1, также известную как сбалансированная F-оценка или F-мера.
fbeta_score(y_true, y_pred, *, beta[, ...])	Вычислить F-бета оценку.
hamming_loss(y_true, y_pred, *[, sample_weight])	Вычисляет среднюю потерю Хэмминга.
jaccard_score(y_true, y_pred, *[, labels, ...])	Коэффициент сходства Жаккара.
log_loss(y_true, y_pred, *[, normalize, ...])	Логарифмические потери, также известные как логистические потери или потери перекрестной энтропии.
multilabel_confusion_matrix(y_true, y_pred, *)	Вычислить матрицу ошибок для каждого класса или образца.
precision_recall_fscore_support(y_true, ...)	Вычислить точность, полноту, F-меру и поддержку для каждого класса.
precision_score(y_true, y_pred, *[, labels, ...])	Вычислить точность.
recall_score(y_true, y_pred, *[, labels, ...])	Вычислить полноту (recall).
roc_auc_score(y_true, y_score, *[, average, ...])	Вычисление площади под кривой рабочих характеристик приемника (ROC AUC) по прогнозным оценкам.
zero_one_loss(y_true, y_pred, *[, ...])	Потеря классификации ноль-один.
d2_log_loss_score(y_true, y_pred, *[, ...])	\(D^2\) функция оценки, доля объясненной логарифмической потери.

И некоторые работают с бинарными и многометочными (но не многоклассовыми) задачами:

average_precision_score(y_true, y_score, *)

Вычислите среднюю точность (AP) из оценок предсказания.

В следующих подразделах мы опишем каждую из этих функций, предварительно представив некоторые замечания об общем API и определении метрики.

3.4.4.1. От бинарной к многоклассовой и многометочной

Некоторые метрики по сути определены для задач бинарной классификации (например, f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительный класс, предполагая по умолчанию, что положительный класс помечен как 1 (хотя это может быть настраиваемо через pos_label параметр).

При расширении бинарной метрики до многоклассовых или многометочных задач данные рассматриваются как набор бинарных проблем, по одной для каждого класса. Затем существует несколько способов усреднения вычислений бинарных метрик по набору классов, каждый из которых может быть полезен в некоторых сценариях. Если доступно, вы должны выбирать среди них с помощью average параметр.

• "macro" просто вычисляет среднее значение бинарных метрик, придавая равный вес каждому классу. В задачах, где редкие классы тем не менее важны, макроусреднение может быть способом выделить их производительность. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макроусреднение будет чрезмерно подчеркивать обычно низкую производительность на редком классе.

• "weighted" учитывает дисбаланс классов, вычисляя среднее бинарных метрик, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных.

• "micro" дает каждой паре образец-класс равный вклад в общую метрику (за исключением случаев, связанных с весом образца). Вместо суммирования метрики по классам, это суммирует делимое и делители, составляющие метрики по классам, для вычисления общего частного. Микро-усреднение может быть предпочтительным в многометочных настройках, включая многоклассовую классификацию, где большинство классов следует игнорировать.

• "samples" применяется только к многометочным задачам. Он не вычисляет показатель для каждого класса, вместо этого вычисляя метрику по истинным и предсказанным классам для каждого образца в оценочных данных и возвращая их (sample_weight-взвешенное) среднее.

• Выбор данных average=None вернет массив с оценкой для каждого класса.

В то время как многоклассовые данные предоставляются метрике, как и бинарные целевые значения, в виде массива меток классов, многометочные данные задаются в виде индикаторной матрицы, в которой ячейка [i, j] имеет значение 1, если образец i имеет метку j и значение 0 в противном случае.

3.4.4.2. Оценка точности

The accuracy_score функция вычисляет точность, либо доля (по умолчанию), либо количество (normalize=False) правильных предсказаний.

scikit-learn-contrib

Если \(\hat{y}_i\) является предсказанным значением \(i\)-й образец и \(y_i\) является соответствующим истинным значением, тогда доля правильных предсказаний по \(n_\text{samples}\) определяется как

\[\texttt{accuracy}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i = y_i)\]

где \(1(x)\) является индикаторная функция.

>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2.0

В случае многометочной классификации с бинарными индикаторами меток:

>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

Примеры

• См. Тест с перестановками для значимости оценки классификации для примера использования метрики точности с перестановками набора данных.

3.4.4.3. Оценка точности top-k

The top_k_accuracy_score функция является обобщением accuracy_score. Разница в том, что предсказание считается правильным, пока истинная метка связана с одним из k наивысшие предсказанные оценки. accuracy_score является частным случаем k = 1.

Функция охватывает бинарный и многоклассовый случаи классификации, но не многометочный случай.

Если \(\hat{f}_{i,j}\) это предсказанный класс для \(i\)-й образец, соответствующий \(j\)-й наибольший предсказанный балл и \(y_i\) является соответствующим истинным значением, тогда доля правильных прогнозов относительно \(n_\text{samples}\) определяется как

\[\texttt{top-k accuracy}(y, \hat{f}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \sum_{j=1}^{k} 1(\hat{f}_{i,j} = y_i)\]

где \(k\) это количество разрешенных догадок и \(1(x)\) является индикаторная функция.

>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
>>> y_score = np.array([[0.5, 0.2, 0.2],
...                     [0.3, 0.4, 0.2],
...                     [0.2, 0.4, 0.3],
...                     [0.7, 0.2, 0.1]])
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
>>> # Not normalizing gives the number of "correctly" classified samples
>>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False)
3.0

3.4.4.4. Сбалансированная точность

The balanced_accuracy_score функция вычисляет сбалансированная точность, что позволяет избежать завышенных оценок производительности на несбалансированных наборах данных. Это макро-среднее значений полноты по классам или, что эквивалентно, сырая точность, где каждый образец взвешивается в соответствии с обратной распространенностью его истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.

В бинарном случае сбалансированная точность равна среднему арифметическому чувствительность (истинная положительная частота) и специфичность (истинно отрицательная частота) или площадь под ROC-кривой с бинарными предсказаниями, а не оценками:

\[\texttt{balanced-accuracy} = \frac{1}{2}\left( \frac{TP}{TP + FN} + \frac{TN}{TN + FP}\right )\]

Если классификатор работает одинаково хорошо на любом классе, этот термин сводится к обычной точности (т.е., количество правильных предсказаний, деленное на общее количество предсказаний).

В отличие от этого, если обычная точность выше случайной только потому, что классификатор использует преимущество несбалансированного тестового набора, то сбалансированная точность, как и следует, упадет до \(\frac{1}{n\_classes}\).

Оценка варьируется от 0 до 1, или когда adjusted=True используется, он масштабируется к диапазону \(\frac{1}{1 - n\_classes}\) до 1 включительно, при этом производительность при случайном оценивании равна 0.

Если \(y_i\) является истинным значением \(i\)-й образец, и \(w_i\) это соответствующий вес выборки, тогда мы корректируем вес выборки на:

\[\hat{w}_i = \frac{w_i}{\sum_j{1(y_j = y_i) w_j}}\]

где \(1(x)\) является индикаторная функция. Учитывая предсказанные \(\hat{y}_i\) для образца \(i\), сбалансированная точность определяется как:

\[\texttt{balanced-accuracy}(y, \hat{y}, w) = \frac{1}{\sum{\hat{w}_i}} \sum_i 1(\hat{y}_i = y_i) \hat{w}_i\]

С adjusted=True, сбалансированная точность сообщает об относительном увеличении от \(\texttt{balanced-accuracy}(y, \mathbf{0}, w) = \frac{1}{n\_classes}\). В бинарном случае это также известно как Статистика Юдена J, или информированность.

Примечание

Многоклассовое определение здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определённого консенсуса:

• Наше определение: [Mosley2013], [Kelleher2015] и [Guyon2015], где [Guyon2015] принять скорректированную версию, чтобы гарантировать, что случайные прогнозы имеют оценку \(0\) и идеальные предсказания имеют оценку \(1\).

• Сбалансированная точность по классам, как описано в [Mosley2013]: вычисляется минимум между точностью и полнотой для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.

• Сбалансированная точность, как описано в [Urbanowicz2015]: среднее чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.

Ссылки

[Guyon2015] (1,2)

I. Guyon, K. Bennett, G. Cawley, H.J. Escalante, S. Escalera, T.K. Ho, N. Macià, B. Ray, M. Saeed, A.R. Statnikov, E. Viegas, Дизайн ChaLearn AutoML Challenge 2015, IJCNN 2015.

[Mosley2013] (1,2)

L. Mosley, Сбалансированный подход к проблеме дисбаланса многоклассовой классификации, IJCV 2010.

[Kelleher2015]

Джон Д. Келлехер, Брайан Мак Нами, Аойф Д'Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры, и тематические исследования, 2015.

[Urbanowicz2015]

Urbanowicz R.J., Moore, J.H. ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения, Evol. Intel. (2015) 8: 89.

3.4.4.5. Каппа Коэна

Функция cohen_kappa_score вычисляет Каппа Коэна статистика. Эта мера предназначена для сравнения разметок разными аннотаторами, а не классификатора с истинными метками.

Оценка каппа — это число от -1 до 1. Оценки выше .8 обычно считаются хорошим согласием; ноль или ниже означает отсутствие согласия (практически случайные метки).

Оценки каппа могут быть вычислены для бинарных или многоклассовых задач, но не для многометочных задач (кроме как путем ручного вычисления оценки на метку) и не для более чем двух аннотаторов.

>>> from sklearn.metrics import cohen_kappa_score
>>> labeling1 = [2, 0, 2, 2, 0, 1]
>>> labeling2 = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(labeling1, labeling2)
0.4285714285714286

3.4.4.6. Матрица ошибок

The confusion_matrix функция оценивает точность классификации, вычисляя матрица ошибок где каждая строка соответствует истинному классу (Википедия и другие источники могут использовать другую конвенцию для осей).

По определению, элемент \(i, j\) в матрице ошибок — это количество наблюдений, фактически находящихся в группе \(i\), но предсказано, что будет в группе \(j\). Вот пример:

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

ConfusionMatrixDisplay можно использовать для визуального представления матрицы ошибок, как показано в Оценить производительность классификатора с помощью матрицы ошибок пример, который создаёт следующую фигуру:

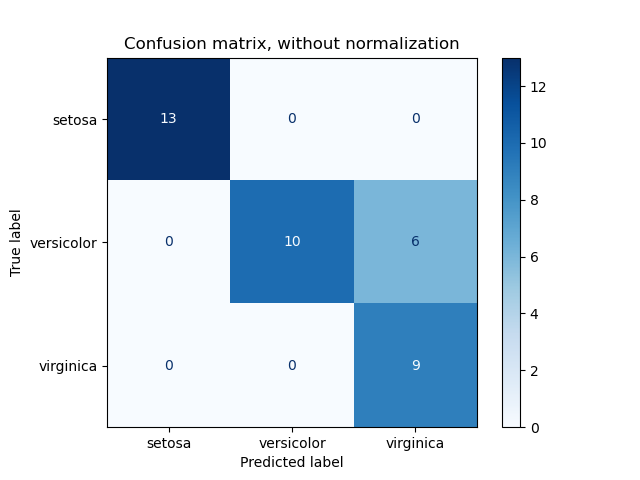
Параметр normalize позволяет отображать отношения вместо подсчётов. Матрицу ошибок можно нормализовать тремя различными способами: 'pred', 'true', и 'all' который разделит подсчеты на сумму каждого столбца, строки или всей матрицы соответственно.

>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
       [0.25 , 0.375]])

Для бинарных задач мы можем получить количество истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных случаев следующим образом:

>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel().tolist()
>>> tn, fp, fn, tp
(2, 1, 2, 3)

С confusion_matrix_at_thresholds мы можем получить истинно отрицательные, ложноположительные, ложноотрицательные и истинно положительные результаты для различных порогов:

>>> from sklearn.metrics import confusion_matrix_at_thresholds
>>> y_true = np.array([0., 0., 1., 1.])
>>> y_score = np.array([0.1, 0.4, 0.35, 0.8])
>>> tns, fps, fns, tps, thresholds = confusion_matrix_at_thresholds(y_true, y_score)
>>> tns
array([2., 1., 1., 0.])
>>> fps
array([0., 1., 1., 2.])
>>> fns
array([1., 1., 0., 0.])
>>> tps
array([1., 1., 2., 2.])
>>> thresholds
array([0.8, 0.4, 0.35, 0.1])

Обратите внимание, что пороги состоят из различных y_score значения в порядке убывания.

Примеры

• См. Оценить производительность классификатора с помощью матрицы ошибок для примера использования матрицы ошибок для оценки качества вывода классификатора.

• См. Распознавание рукописных цифр для примера использования матрицы ошибок для классификации рукописных цифр.

• См. Классификация текстовых документов с использованием разреженных признаков Вы пробовали

3.4.4.7. Отчет о классификации

The classification_report функция строит текстовый отчет, показывающий основные метрики классификации. Вот небольшой пример с пользовательскими target_names и выведенные метки:

>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
              precision    recall  f1-score   support

     class 0       0.67      1.00      0.80         2
     class 1       0.00      0.00      0.00         1
     class 2       1.00      0.50      0.67         2

    accuracy                           0.60         5
   macro avg       0.56      0.50      0.49         5
weighted avg       0.67      0.60      0.59         5

Примеры

• См. Распознавание рукописных цифр для примера использования отчета классификации для рукописных цифр.

• См. Пользовательская стратегия повторного обучения для поиска по сетке с кросс-валидацией для примера использования отчёта классификации при поиске по сетке с вложенной перекрёстной проверкой.

3.4.4.8. Потеря Хэмминга

The hamming_loss вычисляет среднюю потерю Хэмминга или Расстояние Хэмминга между двумя наборами выборок.

Если \(\hat{y}_{i,j}\) является предсказанным значением для \(j\)-я метка данного образца \(i\), \(y_{i,j}\) является соответствующим истинным значением, \(n_\text{samples}\) — это количество образцов и \(n_\text{labels}\) это количество меток, тогда потеря Хэмминга \(L_{Hamming}\) определяется как:

\[L_{Hamming}(y, \hat{y}) = \frac{1}{n_\text{samples} * n_\text{labels}} \sum_{i=0}^{n_\text{samples}-1} \sum_{j=0}^{n_\text{labels} - 1} 1(\hat{y}_{i,j} \not= y_{i,j})\]

где \(1(x)\) является индикаторная функция.

Уравнение выше не выполняется в случае многоклассовой классификации. Пожалуйста, обратитесь к примечанию ниже для получения дополнительной информации.

>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25

В случае многометочной классификации с бинарными индикаторами меток:

>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75

Примечание

В многоклассовой классификации потеря Хэмминга соответствует расстоянию Хэмминга между y_true и y_pred что похоже на Потеря ноль-один функции. Однако, в то время как zero-one loss штрафует наборы предсказаний, которые не строго соответствуют истинным наборам, Hamming loss штрафует отдельные метки. Таким образом, Hamming loss, ограниченная сверху zero-one loss, всегда находится между нулем и единицей включительно; и предсказание правильного подмножества или надмножества истинных меток даст Hamming loss между нулем и единицей, исключая границы.

3.4.4.9. Точность, полнота и F-меры

Интуитивно, точность это способность классификатора не помечать как положительный образец, который является отрицательным, и полнота это способность классификатора находить все положительные выборки.

The F-мера (\(F_\beta\) и \(F_1\) меры) можно интерпретировать как взвешенное гармоническое среднее точности и полноты. \(F_\beta\) метрика достигает наилучшего значения при 1 и наихудшего при 0. При \(\beta = 1\), \(F_\beta\) и \(F_1\) эквивалентны, а полнота и точность одинаково важны.

The precision_recall_curve вычисляет кривую точности-полноты из истинных меток и оценки, предоставленной классификатором, путем варьирования порога принятия решения.

The average_precision_score функция вычисляет average precision (AP) из оценок предсказания. Значение находится между 0 и 1, и чем выше, тем лучше. AP определяется как

\[\text{AP} = \sum_n (R_n - R_{n-1}) P_n\]

где \(P_n\) и \(R_n\) это точность и полнота на n-м пороге. При случайных предсказаниях AP - это доля положительных образцов.

Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-полноты. В настоящее время, average_precision_score не реализует никакой интерполированный вариант. Ссылки [Davis2006] и [Flach2015] объясняют, почему линейная интерполяция точек на кривой точности-полноты дает излишне оптимистичную оценку производительности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой по правилу трапеций в auc. [Chen2024] сравнивает различные стратегии интерполяции, чтобы продемонстрировать их эффекты.

Несколько функций позволяют анализировать показатели точности, полноты и F-меры:

average_precision_score(y_true, y_score, *)	Вычислите среднюю точность (AP) из оценок предсказания.
f1_score(y_true, y_pred, *[, labels, ...])	Вычислите оценку F1, также известную как сбалансированная F-оценка или F-мера.
fbeta_score(y_true, y_pred, *, beta[, ...])	Вычислить F-бета оценку.
precision_recall_curve(y_true, y_score, *[, ...])	Вычислите пары точность-полнота для различных порогов вероятности.
precision_recall_fscore_support(y_true, ...)	Вычислить точность, полноту, F-меру и поддержку для каждого класса.
precision_score(y_true, y_pred, *[, labels, ...])	Вычислить точность.
recall_score(y_true, y_pred, *[, labels, ...])	Вычислить полноту (recall).

Обратите внимание, что precision_recall_curve функция ограничена бинарным случаем. The average_precision_score функция поддерживает многоклассовые и многометочные форматы, вычисляя оценку каждого класса в режиме "Один против всех" (OvR) и усредняя их или нет в зависимости от ее average значение аргумента.

The PrecisionRecallDisplay.from_estimator и PrecisionRecallDisplay.from_predictions функции построят кривую precision-recall следующим образом.

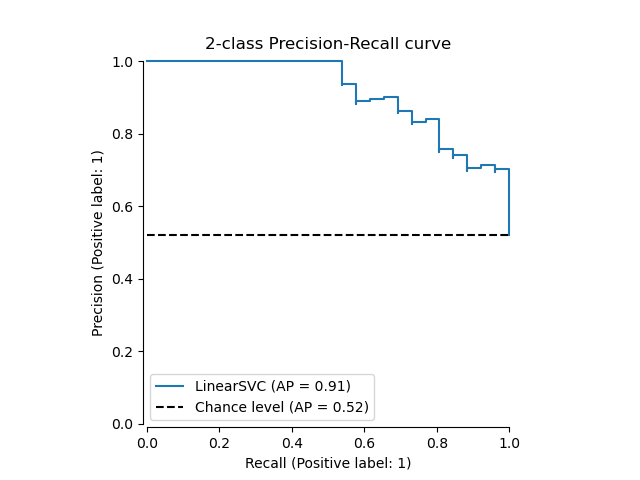
Примеры

• См. Пользовательская стратегия повторного обучения для поиска по сетке с кросс-валидацией для примера precision_score и recall_score использование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой.

• См. Precision-Recall для примера precision_recall_curve использование для оценки качества выхода классификатора.

Ссылки

[Manning2008]

C.D. Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval, 2008.

[Everingham2010]

M. Everingham, L. Van Gool, C.K.I. Williams, J. Winn, A. Zisserman, Задача Pascal Visual Object Classes (VOC), IJCV 2010.

[Davis2006]

J. Davis, M. Goadrich, Связь между кривыми Precision-Recall и ROC, ICML 2006.

[Flach2015]

P.A. Flach, M. Kull, Кривые Precision-Recall-Gain: правильный анализ PR, NIPS 2015.

[Chen2024]

W. Chen, C. Miao, Z. Zhang, C.S. Fung, R. Wang, Y. Chen, Y. Qian, L. Cheng, K.Y. Yip, S.K Tsui, Q. Cao, Распространённые программные инструменты производят противоречивые и чрезмерно оптимистичные значения AUPRC, Genome Biology 2024.

3.4.4.9.1. Бинарная классификация

В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли это предсказание внешнему суждению (иногда известному как «наблюдение»). Исходя из этих определений, мы можем сформулировать следующую таблицу:

	Фактический класс (наблюдение)
Предсказанный класс (ожидание)	tp (true positive) Правильный результат	fp (ложноположительный) Неожиданный результат
	fn (ложноотрицательный) Пропущенный результат	tn (истинно отрицательный) Правильное отсутствие результата

В этом контексте мы можем определить понятия точности и полноты:

\[\text{precision} = \frac{\text{tp}}{\text{tp} + \text{fp}},\]

\[\text{recall} = \frac{\text{tp}}{\text{tp} + \text{fn}},\]

Для полного примера масштабирования вне ядра в задаче классификации текста см.

F-мера — это взвешенное гармоническое среднее точности и полноты, где вклад точности в среднее взвешивается некоторым параметром \(\beta\):

\[F_\beta = (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \text{precision} + \text{recall}}\]

Чтобы избежать деления на ноль, когда точность и полнота равны нулю, Scikit-Learn вычисляет F-меру по этой эквивалентной формуле:

\[F_\beta = \frac{(1 + \beta^2) \text{tp}}{(1 + \beta^2) \text{tp} + \text{fp} + \beta^2 \text{fn}}\]

Обратите внимание, что эта формула всё ещё не определена, когда нет истинно положительных, ложноположительных или ложноотрицательных случаев. По умолчанию F-1 для набора исключительно истинно отрицательных случаев рассчитывается как 0, однако это поведение можно изменить с помощью zero_division параметр. Вот несколько небольших примеров в бинарной классификации:

>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([0.66, 1.        ]), array([1. , 0.5]), array([0.71, 0.83]), array([2, 2]))


>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([0.5       , 0.66, 0.5       , 1.        , 1.        ])
>>> recall
array([1. , 1. , 0.5, 0.5, 0. ])
>>> threshold
array([0.1 , 0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.83

3.4.4.9.2. Многоклассовая и многометочная классификация

В многоклассовой и многометочной классификации понятия точности, полноты и F-меры могут применяться к каждой метке независимо. Существует несколько способов объединения результатов по меткам, задаваемых параметром average аргумент для average_precision_score, f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функции, как описано выше.

Обратите внимание на следующие особенности при усреднении:

• Если все метки включены, «микро»-усреднение в многоклассовой настройке даст точность, полноту и \(F\) которые все идентичны точности.

• “взвешенное” усреднение может дать F-оценку, которая не находится между точностью и полнотой.

• усреднение "macro" для F-меры рассчитывается как среднее арифметическое по F-мерам для каждого метки/класса, а не как среднее гармоническое от средних арифметических точности и полноты. Оба расчета можно встретить в литературе, но они не эквивалентны, см. [OB2019] подробности.

Чтобы сделать это более явным, рассмотрим следующую нотацию:

• \(y\) набор true \((sample, label)\) пары

• \(\hat{y}\) набор предсказанный \((sample, label)\) пары

• \(L\) множество меток

• \(S\) набор образцов

• \(y_s\) подмножество \(y\) с выборкой \(s\), т.е. \(y_s := \left\{(s', l) \in y | s' = s\right\}\)

• \(y_l\) подмножество \(y\) с меткой \(l\)

• аналогично, \(\hat{y}_s\) и \(\hat{y}_l\) являются подмножествами \(\hat{y}\)

• \(P(A, B) := \frac{\left| A \cap B \right|}{\left|B\right|}\) для некоторых наборов \(A\) и \(B\)

• \(R(A, B) := \frac{\left| A \cap B \right|}{\left|A\right|}\) (Соглашения различаются по обработке \(A = \emptyset\); эта реализация использует \(R(A, B):=0\), и аналогично для \(P\).)

• \(F_\beta(A, B) := \left(1 + \beta^2\right) \frac{P(A, B) \times R(A, B)}{\beta^2 P(A, B) + R(A, B)}\)

Тогда метрики определяются как:

average	Precision	Полнота	F_beta
"micro"	\(P(y, \hat{y})\)	\(R(y, \hat{y})\)	\(F_\beta(y, \hat{y})\)
"samples"	\(\frac{1}{\left|S\right|} \sum_{s \in S} P(y_s, \hat{y}_s)\)	\(\frac{1}{\left|S\right|} \sum_{s \in S} R(y_s, \hat{y}_s)\)	\(\frac{1}{\left|S\right|} \sum_{s \in S} F_\beta(y_s, \hat{y}_s)\)
"macro"	\(\frac{1}{\left|L\right|} \sum_{l \in L} P(y_l, \hat{y}_l)\)	\(\frac{1}{\left|L\right|} \sum_{l \in L} R(y_l, \hat{y}_l)\)	\(\frac{1}{\left|L\right|} \sum_{l \in L} F_\beta(y_l, \hat{y}_l)\)
"weighted"	\(\frac{1}{\sum_{l \in L} \left|y_l\right|} \sum_{l \in L} \left|y_l\right| P(y_l, \hat{y}_l)\)	\(\frac{1}{\sum_{l \in L} \left|y_l\right|} \sum_{l \in L} \left|y_l\right| R(y_l, \hat{y}_l)\)	\(\frac{1}{\sum_{l \in L} \left|y_l\right|} \sum_{l \in L} \left|y_l\right| F_\beta(y_l, \hat{y}_l)\)
None	\(\langle P(y_l, \hat{y}_l) | l \in L \rangle\)	\(\langle R(y_l, \hat{y}_l) | l \in L \rangle\)	\(\langle F_\beta(y_l, \hat{y}_l) | l \in L \rangle\)

>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')
0.22
>>> metrics.recall_score(y_true, y_pred, average='micro')
0.33
>>> metrics.f1_score(y_true, y_pred, average='weighted')
0.267
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.238
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
(array([0.667, 0., 0.]), array([1., 0., 0.]), array([0.714, 0., 0.]), array([2, 2, 2]))

Для многоклассовой классификации с "отрицательным классом" можно исключить некоторые метки:

>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0

Аналогично, метки, отсутствующие в выборке данных, могут учитываться в макроусреднении.

>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
0.166

Ссылки

[OB2019]

Opitz, J., & Burst, S. (2019). «Macro f1 и macro f1.»

3.4.4.10. Коэффициент сходства Жаккара

The jaccard_score функция вычисляет среднее значение Коэффициенты сходства Жаккара, также называемый индексом Жаккара, между парами наборов меток.

Коэффициент сходства Жаккара с набором истинных меток \(y\) и предсказанный набор меток \(\hat{y}\), определяется как

\[J(y, \hat{y}) = \frac{|y \cap \hat{y}|}{|y \cup \hat{y}|}.\]

The jaccard_score (как precision_recall_fscore_support) изначально применяется к бинарным целевым переменным. Вычисляя его по множествам, его можно расширить для применения к многометочным и многоклассовым задачам с помощью average (см. выше).

В бинарном случае:

>>> import numpy as np
>>> from sklearn.metrics import jaccard_score
>>> y_true = np.array([[0, 1, 1],
...                    [1, 1, 0]])
>>> y_pred = np.array([[1, 1, 1],
...                    [1, 0, 0]])
>>> jaccard_score(y_true[0], y_pred[0])
0.6666

В случае 2D сравнения (например, сходства изображений):

>>> jaccard_score(y_true, y_pred, average="micro")
0.6

В случае многометочной классификации с бинарными индикаторами меток:

>>> jaccard_score(y_true, y_pred, average='samples')
0.5833
>>> jaccard_score(y_true, y_pred, average='macro')
0.6666
>>> jaccard_score(y_true, y_pred, average=None)
array([0.5, 0.5, 1. ])

Многоклассовые задачи бинаризуются и обрабатываются как соответствующие многометочные задачи:

>>> y_pred = [0, 2, 1, 2]
>>> y_true = [0, 1, 2, 2]
>>> jaccard_score(y_true, y_pred, average=None)
array([1. , 0. , 0.33])
>>> jaccard_score(y_true, y_pred, average='macro')
0.44
>>> jaccard_score(y_true, y_pred, average='micro')
0.33

3.4.4.11. Потеря на шарнире

The hinge_loss функция вычисляет среднее расстояние между моделью и данными с использованием hinge loss, односторонняя метрика, которая учитывает только ошибки предсказания. (Функция потерь hinge используется в классификаторах с максимальным зазором, таких как машины опорных векторов.)

Если истинная метка \(y_i\) бинарной задачи классификации кодируется как \(y_i=\left\{-1, +1\right\}\) для каждой выборки \(i\); и \(w_i\) является соответствующим предсказанным решением (массив формы (n_samples,) как вывод от decision_function метод), тогда функция потерь hinge определяется как:

\[L_\text{Hinge}(y, w) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \max\left\{1 - w_i y_i, 0\right\}\]

Если меток больше двух, hinge_loss использует многоклассовый вариант от Crammer & Singer. Здесь это статья, описывающая его.

В данном случае предсказанное решение представляет собой массив формы (n_samples, n_labels). Если \(w_{i, y_i}\) это предсказанное решение для истинной метки \(y_i\) из \(i\)-й образец; и \(\hat{w}_{i, y_i} = \max\left\{w_{i, y_j}~|~y_j \ne y_i \right\}\) является максимумом предсказанных решений для всех других меток, тогда многоклассовая шарнирная функция потерь определяется как:

\[L_\text{Hinge}(y, w) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} \max\left\{1 + \hat{w}_{i, y_i} - w_{i, y_i}, 0\right\}\]

Вот небольшой пример, демонстрирующий использование hinge_loss функция с классификатором svm в задаче бинарной классификации:

>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(random_state=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18,  2.36,  0.09])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.3

Вот пример, демонстрирующий использование hinge_loss функция с классификатором svm в многоклассовой задаче:

>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC()
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels=labels)
0.56

3.4.4.12. Логарифмическая потеря

Логистическая потеря, также называемая потерей логистической регрессии или кросс-энтропийной потерей, определена на вероятностных оценках. Она часто используется в (мультиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах EM-алгоритма, и может использоваться для оценки вероятностных выходов (predict_proba) классификатора вместо его дискретных предсказаний.

Для бинарной классификации с истинной меткой \(y \in \{0,1\}\) и оценку вероятности \(\hat{p} \approx \operatorname{Pr}(y = 1)\), логарифмическая потеря на образец — это отрицательное логарифмическое правдоподобие классификатора при заданной истинной метке:

\[L_{\log}(y, \hat{p}) = -\log \operatorname{Pr}(y|\hat{p}) = -(y \log (\hat{p}) + (1 - y) \log (1 - \hat{p}))\]

Это распространяется на многоклассовый случай следующим образом. Пусть истинные метки для набора образцов закодированы как 1-из-K бинарная индикаторная матрица \(Y\), т.е., \(y_{i,k} = 1\) если образец \(i\) имеет метку \(k\) взяты из набора \(K\) метки. Пусть \(\hat{P}\) будет матрицей оценок вероятностей, с элементами \(\hat{p}_{i,k} \approx \operatorname{Pr}(y_{i,k} = 1)\). Тогда логарифмическая потеря всего набора равна

\[L_{\log}(Y, \hat{P}) = -\log \operatorname{Pr}(Y|\hat{P}) = - \frac{1}{N} \sum_{i=0}^{N-1} \sum_{k=0}^{K-1} y_{i,k} \log \hat{p}_{i,k}\]

Чтобы увидеть, как это обобщает бинарную логарифмическую потерю, приведённую выше, обратите внимание, что в бинарном случае, \(\hat{p}_{i,0} = 1 - \hat{p}_{i,1}\) и \(y_{i,0} = 1 - y_{i,1}\), так что раскрывая внутреннюю сумму по \(y_{i,k} \in \{0,1\}\) дает бинарную логарифмическую потерю.

The log_loss функция вычисляет логарифмическую потерю по заданному списку истинных меток и матрице вероятностей, возвращаемой методом predict_proba метод.

>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738

Первый [.9, .1] в y_pred обозначает 90% вероятность того, что первый образец имеет метку 0. Логарифмическая потеря неотрицательна.

3.4.4.13. Коэффициент корреляции Мэтьюса

The matthews_corrcoef функция вычисляет Коэффициент корреляции Мэтьюса (MCC) для бинарных классов. Цитируя Википедию:

«Коэффициент корреляции Мэтьюса используется в машинном обучении как мера качества бинарных (двухклассовых) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно считается сбалансированной мерой, которую можно использовать, даже если классы сильно различаются по размеру. MCC по сути является коэффициентом корреляции со значением от -1 до +1. Коэффициент +1 представляет идеальный прогноз, 0 — средний случайный прогноз, а -1 — обратный прогноз. Эта статистика также известна как коэффициент фи.»

В бинарном (двухклассовом) случае, \(tp\), \(tn\), \(fp\) и \(fn\) соответственно количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных случаев, MCC определяется как

\[MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.\]

В многоклассовом случае коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix \(C\) для \(K\) классов. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:

• \(t_k=\sum_{i}^{K} C_{ik}\) количество раз, когда класс \(k\) действительно произошло,

• \(p_k=\sum_{i}^{K} C_{ki}\) количество раз, когда класс \(k\) был предсказан,

• \(c=\sum_{k}^{K} C_{kk}\) общее количество правильно предсказанных образцов,

• \(s=\sum_{i}^{K} \sum_{j}^{K} C_{ij}\) общее количество выборок.

Тогда многоклассовый MCC определяется как:

\[MCC = \frac{ c \times s - \sum_{k}^{K} p_k \times t_k }{\sqrt{ (s^2 - \sum_{k}^{K} p_k^2) \times (s^2 - \sum_{k}^{K} t_k^2) }}\]

Когда меток больше двух, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения истинных меток. Максимальное значение всегда +1. Для дополнительной информации см. [WikipediaMCC2021].

Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функция:

>>> from sklearn.metrics import matthews_corrcoef
>>> y_true = [+1, +1, +1, -1]
>>> y_pred = [+1, -1, +1, +1]
>>> matthews_corrcoef(y_true, y_pred)
-0.33

Ссылки

[WikipediaMCC2021]

Участники Википедии. Коэффициент фи. Википедия, Свободная энциклопедия. 21 апреля 2021, 12:21 CEST. Доступно по адресу: https://en.wikipedia.org/wiki/Phi_coefficient Дата обращения: 21 апреля 2021 г.

3.4.4.14. Матрица ошибок для многометочной классификации

The multilabel_confusion_matrix функция вычисляет поклассовую (по умолчанию) или пообразцовую (samplewise=True) многометочную матрицу ошибок для оценки точности классификации. multilabel_confusion_matrix также обрабатывает многоклассовые данные как если бы они были многометочными, так как это преобразование обычно применяется для оценки многоклассовых проблем с бинарными метриками классификации (такими как точность, полнота и т.д.).

При вычислении многометочной матрицы ошибок по классам \(C\), количество истинно отрицательных для класса \(i\) является \(C_{i,0,0}\), false negatives это \(C_{i,1,0}\), истинные положительные результаты — это \(C_{i,1,1}\) и ложные срабатывания - это \(C_{i,0,1}\).

Вот пример, демонстрирующий использование multilabel_confusion_matrix функция с матрица индикаторов мультиметок вход:

>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
...                    [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
...                    [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
        [0, 1]],

       [[1, 0],
        [0, 1]],

       [[0, 1],
        [1, 0]]])

Или матрица ошибок может быть построена для меток каждого образца:

>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
        [1, 1]],

       [[1, 1],
        [0, 1]]])

Вот пример, демонстрирующий использование multilabel_confusion_matrix функция с многоклассовый вход:

>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
...                             labels=["ant", "bird", "cat"])
array([[[3, 1],
        [0, 2]],

       [[5, 0],
        [1, 0]],

       [[2, 1],
        [1, 2]]])

Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функцию для расчета полноты (или чувствительности), специфичности, ложноположительной и ложноотрицательной частоты для каждого класса в задаче с входными данными в виде матрицы индикаторов мультиметок.

Вычисление полнота (также называемая истинной положительной частотой или чувствительностью) для каждого класса:

>>> y_true = np.array([[0, 0, 1],
...                    [0, 1, 0],
...                    [1, 1, 0]])
>>> y_pred = np.array([[0, 1, 0],
...                    [0, 0, 1],
...                    [1, 1, 0]])
>>> mcm = multilabel_confusion_matrix(y_true, y_pred)
>>> tn = mcm[:, 0, 0]
>>> tp = mcm[:, 1, 1]
>>> fn = mcm[:, 1, 0]
>>> fp = mcm[:, 0, 1]
>>> tp / (tp + fn)
array([1. , 0.5, 0. ])

Вычисление специфичность (также называемая истинной отрицательной частотой) для каждого класса:

>>> tn / (tn + fp)
array([1. , 0. , 0.5])

Вычисление fall out (также называемая частотой ложных срабатываний) для каждого класса:

>>> fp / (fp + tn)
array([0. , 1. , 0.5])

Вычисление частота пропусков (также называемая частотой ложноотрицательных результатов) для каждого класса:

>>> fn / (fn + tp)
array([0. , 0.5, 1. ])

3.4.4.15. Рабочая характеристика приемника (ROC)

Функция roc_curve вычисляет кривая рабочих характеристик приемника, или ROC-кривая. Цитируя Википедию:

«Рабочая характеристика приемника (ROC), или просто кривая ROC, — это графический график, который иллюстрирует производительность бинарной классификационной системы при изменении порога дискриминации. Он создается путем построения доли истинно положительных результатов из положительных (TPR = истинно положительная частота) против доли ложноположительных результатов из отрицательных (FPR = ложноположительная частота) при различных настройках порога. TPR также известна как чувствительность, а FPR — это единица минус специфичность или истинно отрицательная частота.»

Эта функция требует истинные бинарные значения и целевые оценки, которые могут быть либо вероятностными оценками положительного класса, значениями уверенности, либо бинарными решениями. Вот небольшой пример использования roc_curve функция:

>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([0. , 0. , 0.5, 0.5, 1. ])
>>> tpr
array([0. , 0.5, 0.5, 1. , 1. ])
>>> thresholds
array([ inf, 0.8 , 0.4 , 0.35, 0.1 ])

По сравнению с метриками, такими как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.

The roc_auc_score функция, обозначаемая ROC-AUC или AUROC, вычисляет площадь под ROC-кривой. Таким образом, информация о кривой суммируется в одном числе.

Следующий рисунок показывает ROC-кривую и ROC-AUC оценку для классификатора, предназначенного для отличия цветка virginica от остальных видов в Набор данных о растениях ириса:

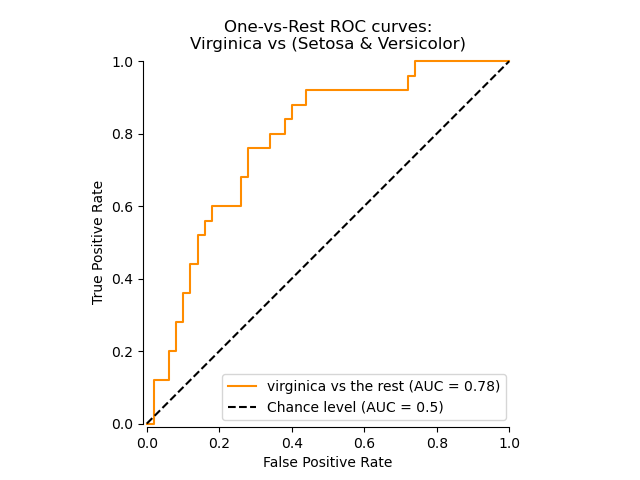
Для получения дополнительной информации см. Статья в Википедии о AUC.

3.4.4.15.1. Бинарный случай

В бинарный случай, вы можете либо предоставить оценки вероятностей, используя classifier.predict_proba() Истинные метки. classifier.decision_function() метод. В случае предоставления оценок вероятности, вероятность класса с "большей меткой" должна быть предоставлена. "Большая метка" соответствует classifier.classes_[1] и, следовательно, classifier.predict_proba(X)[:, 1]. Следовательно, y_score параметр имеет размер (n_samples,).

>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.metrics import roc_auc_score
>>> X, y = load_breast_cancer(return_X_y=True)
>>> clf = LogisticRegression().fit(X, y)
>>> clf.classes_
array([0, 1])

Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].

>>> y_score = clf.predict_proba(X)[:, 1]
>>> roc_auc_score(y, y_score)
0.99

В противном случае мы можем использовать не пороговые значения решений

>>> roc_auc_score(y, clf.decision_function(X))
0.99

3.4.4.15.2. Многоклассовый случай

The roc_auc_score функция также может использоваться в многоклассовая классификация. В настоящее время поддерживаются две стратегии усреднения: алгоритм один-против-одного вычисляет среднее попарных оценок ROC AUC, а алгоритм один-против-всех вычисляет среднее оценок ROC AUC для каждого класса против всех остальных классов. В обоих случаях предсказанные метки предоставляются в массиве со значениями от 0 до n_classes, и оценки соответствуют вероятностным оценкам того, что образец принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание (average='macro') и по распространённости (average='weighted').

Алгоритм один-против-одного

Вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC для многоклассовой классификации, взвешенную равномерно:

\[\frac{1}{c(c-1)}\sum_{j=1}^{c}\sum_{k > j}^c (\text{AUC}(j | k) + \text{AUC}(k | j))\]

где \(c\) - это количество классов, а \(\text{AUC}(j | k)\) является AUC с классом \(j\) как положительный класс и класс \(k\) как отрицательный класс. В общем случае, \(\text{AUC}(j | k) \neq \text{AUC}(k | j)\) в многоклассовом случае. Этот алгоритм используется путём установки ключевого аргумента multiclass to 'ovo' и average to 'macro'.

The [HT2001] метрика AUC для многоклассовой классификации может быть расширена с учетом распространенности:

\[\frac{1}{c(c-1)}\sum_{j=1}^{c}\sum_{k > j}^c p(j \cup k)( \text{AUC}(j | k) + \text{AUC}(k | j))\]

где \(c\) — это количество классов. Этот алгоритм используется путем установки ключевого аргумента multiclass to 'ovo' и average to 'weighted'. 'weighted' опция возвращает взвешенное по распространенности среднее, как описано в [FC2009].

Алгоритм One-vs-rest

Вычисляет AUC каждого класса против остальных [PD2000]. Алгоритм функционально идентичен многометочному случаю. Чтобы включить этот алгоритм, установите аргумент ключевого слова multiclass to 'ovr'. Кроме того, 'macro' [F2006] и 'weighted' [F2001] усреднение, OvR поддерживает 'micro' усреднение.

В приложениях, где высокая частота ложных срабатываний недопустима, параметр max_fpr of roc_auc_score может использоваться для обобщения ROC кривой до заданного предела.

Следующий рисунок показывает микроусреднённую ROC-кривую и соответствующий ей ROC-AUC-показатель для классификатора, предназначенного для различения различных видов в Набор данных о растениях ириса:

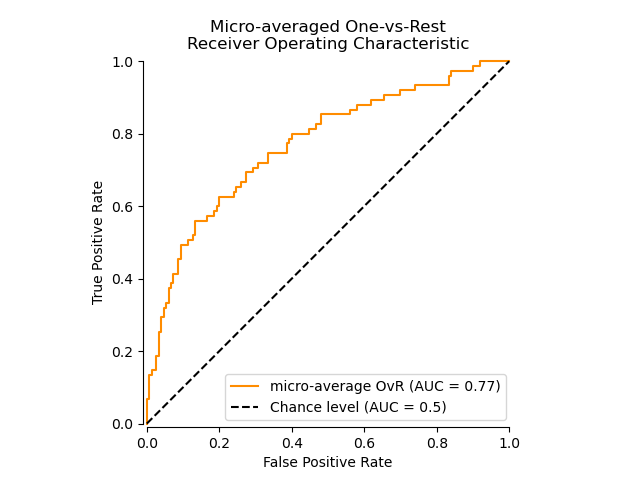
3.4.4.15.3. Многометочный случай

В многометочная классификация, roc_auc_score функция расширена усреднением по меткам как выше. В этом случае вы должны предоставить y_score формы (n_samples, n_classes). Таким образом, при использовании оценок вероятностей необходимо выбирать вероятность класса с большей меткой для каждого выхода.

>>> from sklearn.datasets import make_multilabel_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> X, y = make_multilabel_classification(random_state=0)
>>> inner_clf = LogisticRegression(random_state=0)
>>> clf = MultiOutputClassifier(inner_clf).fit(X, y)
>>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)])
>>> roc_auc_score(y, y_score, average=None)
array([0.828, 0.851, 0.94, 0.87, 0.95])

И значения решений не требуют такой обработки.

>>> from sklearn.linear_model import RidgeClassifierCV
>>> clf = RidgeClassifierCV().fit(X, y)
>>> y_score = clf.decision_function(X)
>>> roc_auc_score(y, y_score, average=None)
array([0.82, 0.85, 0.93, 0.87, 0.94])

Примеры

• См. Многоклассовая рабочая характеристика приемника (ROC) для примера использования ROC для оценки качества вывода классификатора.

• См. Рабочая характеристика приёмника (ROC) с перекрёстной проверкой для примера использования ROC для оценки качества выходных данных классификатора с использованием перекрестной проверки.

• См. Моделирование распределения видов для примера использования ROC для моделирования распределения видов.

Ссылки

[HT2001] (1,2)

Hand, D.J. and Till, R.J., (2001). Простое обобщение площади под ROC-кривой для задач классификации с несколькими классами. Machine learning, 45(2), pp. 171-186.

[FC2009]

Ferri, Cèsar & Hernandez-Orallo, Jose & Modroiu, R. (2009). Экспериментальное сравнение показателей производительности для классификации. Pattern Recognition Letters. 30. 27-38.

[PD2000]

Провост, Ф., Домингос, П. (2000). Хорошо обученные PETs: Улучшение деревьев оценки вероятности (Раздел 6.2), CeDER Working Paper #IS-00-04, Stern School of Business, Нью-Йоркский университет.

[F2006]

Fawcett, T., 2006. Введение в ROC-анализ. Pattern Recognition Letters, 27(8), стр. 861-874.

[F2001]

Fawcett, T., 2001. Использование наборов правил для максимизации производительности ROC В Data Mining, 2001. Proceedings IEEE International Conference, стр. 131-138.

3.4.4.16. Компромисс ошибок обнаружения (DET)

Функция det_curve вычисляет кривую компромисса ошибок обнаружения (DET) [WikipediaDET2017]. Цитируя Википедию:

“График компромисса ошибок обнаружения (DET) — это графическое представление частот ошибок для бинарных классификационных систем, отображающее частоту ложных отказов против частоты ложных принятий. Оси x и y масштабируются нелинейно с помощью их стандартных нормальных отклонений (или просто логарифмическим преобразованием), что дает кривые компромисса, которые более линейны, чем ROC-кривые, и используют большую часть области изображения для выделения различий важности в критической рабочей области.”

Кривые DET — это вариант кривых рабочих характеристик приемника (ROC), где по оси y откладывается частота ложных отрицаний вместо частоты истинных положительных срабатываний. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования с \(\phi^{-1}\) (с \(\phi\) является кумулятивной функцией распределения). Полученные кривые производительности явно визуализируют компромисс между типами ошибок для заданных алгоритмов классификации. См. [Martin1997] для примеров и дальнейшей мотивации.

Этот рисунок сравнивает ROC и DET кривые двух примеров классификаторов на одной задаче классификации:

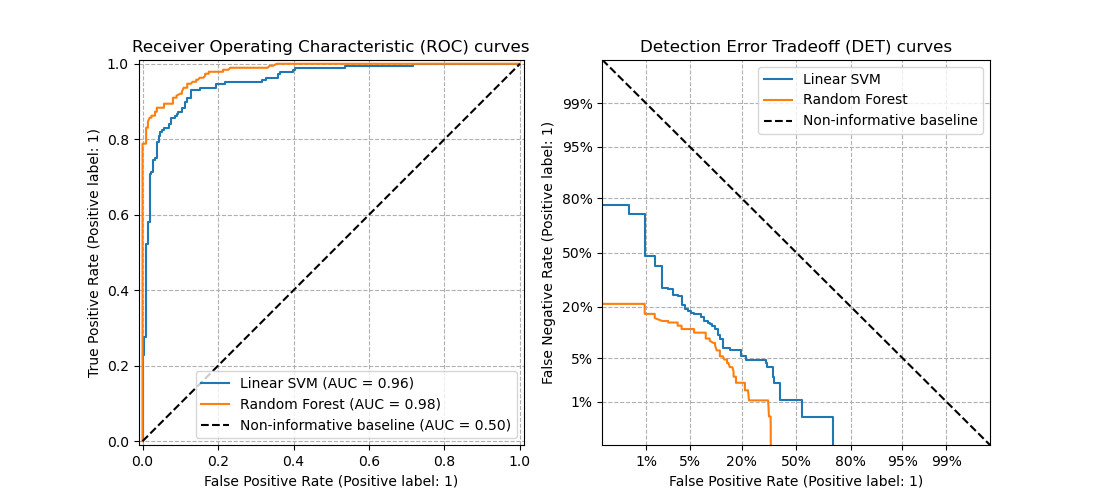
Свойства

• Кривые DET образуют линейную кривую в шкале нормального отклонения, если оценки обнаружения распределены нормально (или близко к нормальному). Это было показано [Navratil2007] that the reverse is not necessarily true and even more general distributions are able to produce linear DET curves.

• Преобразование масштаба нормального отклонения распределяет точки таким образом, что занимается сравнительно большее пространство графика. Поэтому кривые с аналогичной классификационной производительностью могут быть легче различимы на графике DET.

• Поскольку False Negative Rate является "обратной" величиной к True Positive Rate, точка совершенства для DET кривых находится в начале координат (в отличие от верхнего левого угла для ROC кривых).

Применения и ограничения

Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить производительность классификатора. Кроме того, кривые DET можно использовать для анализа порогов и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.

С другой стороны, кривые DET не предоставляют свою метрику в виде одного числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации метрики, такие как производная площадь под кривой ROC, могут быть более подходящими.

Примеры

• См. Кривая компромисса ошибок обнаружения (DET) для примера сравнения между кривыми рабочих характеристик приемника (ROC) и кривыми компромисса ошибок обнаружения (DET).

Ссылки

[WikipediaDET2017]

Wikipedia contributors. Detection error tradeoff. Wikipedia, The Free Encyclopedia. September 4, 2017, 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054. Доступ 19 февраля 2018 г.

[Martin1997]

A. Martin, G. Doddington, T. Kamm, M. Ordowski, and M. Przybocki, Кривая DET в оценке производительности задачи обнаружения, NIST 1997.

[Navratil2007]

J. Navratil и D. Klusacek, “О линейных DET”, 2007 IEEE International Conference on Acoustics, Speech and Signal Processing - ICASSP ‘07, Honolulu, HI, 2007, pp. IV-229-IV-232.

3.4.4.17. Потеря ноль-один

The zero_one_loss функция вычисляет сумму или среднее значение потерь классификации 0-1 (\(L_{0-1}\)) над \(n_{\text{samples}}\). По умолчанию функция нормализует по выборке. Чтобы получить сумму \(L_{0-1}\), установите normalize to False.

В многометочной классификации zero_one_loss оценивает подмножество как единицу, если его метки строго соответствуют прогнозам, и как ноль, если есть любые ошибки. По умолчанию функция возвращает процент неправильно предсказанных подмножеств. Чтобы получить количество таких подмножеств, установите normalize to False.

Если \(\hat{y}_i\) является предсказанным значением \(i\)-й образец и \(y_i\) является соответствующим истинным значением, тогда 0-1 потери \(L_{0-1}\) определяется как:

\[L_{0-1}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples}-1} 1(\hat{y}_i \not= y_i)\]

где \(1(x)\) является индикаторная функция. Нулевая-единичная функция потерь также может быть вычислена как \(\text{zero-one loss} = 1 - \text{accuracy}\).

>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1.0

В многометочном случае с бинарными индикаторами меток, где первый набор меток [0,1] имеет ошибку:

>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5

>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)),  normalize=False)
1.0

Примеры

• См. Рекурсивное исключение признаков с перекрестной проверкой для примера использования нулевой-единичной потери для выполнения рекурсивного отбора признаков с кросс-валидацией.

3.4.4.18. Потеря по шкале Брайера

The brier_score_loss функция вычисляет Оценка Брайера для бинарных и многоклассовых вероятностных прогнозов и эквивалентна средней квадратичной ошибке. Цитируя Википедию:

«Оценка Брайера — это строго правильное правило оценки, которое измеряет точность вероятностных прогнозов. […] [Она] применима к задачам, в которых прогнозы должны присваивать вероятности набору взаимоисключающих дискретных исходов или классов.»

Пусть истинные метки для набора \(N\) точки данных могут быть закодированы как 1-из-K бинарная индикаторная матрица \(Y\), т.е., \(y_{i,k} = 1\) если образец \(i\) имеет метку \(k\) взяты из набора \(K\) метки. Пусть \(\hat{P}\) будет матрицей оценок вероятностей с элементами \(\hat{p}_{i,k} \approx \operatorname{Pr}(y_{i,k} = 1)\)Следуя исходному определению от [Brier1950], оценка Брайера даётся как:

\[BS(Y, \hat{P}) = \frac{1}{N}\sum_{i=0}^{N-1}\sum_{k=0}^{K-1}(y_{i,k} - \hat{p}_{i,k})^{2}\]

Оценка Брайера лежит в интервале \([0, 2]\) и чем ниже значение, тем лучше оценки вероятностей (средняя квадратичная разница меньше). Фактически, оценка Брайера является строго правильным правилом оценки, что означает, что она достигает наилучшего результата только тогда, когда оценённые вероятности равны истинным.

Обратите внимание, что в бинарном случае оценка Брайера обычно делится на два и находится в диапазоне между \([0,1]\). Для бинарных целей \(y_i \in \{0, 1\}\) и вероятностные оценки \(\hat{p}_i \approx \operatorname{Pr}(y_i = 1)\) для положительного класса оценка Брайера тогда равна:

\[BS(y, \hat{p}) = \frac{1}{N} \sum_{i=0}^{N - 1}(y_i - \hat{p}_i)^2\]

The brier_score_loss функция вычисляет оценку Брайера по заданным истинным меткам и предсказанным вероятностям, возвращаемым методом оценщика predict_proba метод. Метод scale_by_half параметр управляет тем, какое из двух вышеуказанных определений следовать.

>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> brier_score_loss(y_true, y_prob)
0.055
>>> brier_score_loss(y_true, 1 - y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(
...    ["eggs", "ham", "spam"],
...    [[0.8, 0.1, 0.1], [0.2, 0.7, 0.1], [0.2, 0.2, 0.6]],
...    labels=["eggs", "ham", "spam"],
... )
0.146

Оценка Брайера может использоваться для оценки того, насколько хорошо калиброван классификатор. Однако более низкая потеря по оценке Брайера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с декомпозицией смещения-дисперсии среднеквадратичной ошибки, потеря по оценке Брайера может быть разложена как сумма потери калибровки и потери уточнения [Bella2012]. Потеря калибровки определяется как среднее квадратичное отклонение от эмпирических вероятностей, полученных из наклона сегментов ROC. Потеря уточнения может быть определена как ожидаемая оптимальная потеря, измеренная площадью под оптимальной кривой затрат. Потеря уточнения может изменяться независимо от потери калибровки, поэтому меньшая потеря по Брайеру не обязательно означает лучше откалиброванную модель. «Только когда потеря уточнения остается неизменной, меньшая потеря по Брайеру всегда означает лучшую калибровку» [Bella2012], [Flach2008].

Примеры

• См. Калибровка вероятностей классификаторов для примера использования потерь по шкале Брайера для выполнения калибровки вероятностей классификаторов.

Ссылки

[Brier1950]

G. Brier, Верификация прогнозов, выраженных в терминах вероятностиУлучшения документации: Добавлен

[Bella2012] (1,2)

Белла, Ферри, Эрнандес-Оральо и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Khosrow-Pour, M. «Машинное обучение: концепции, методологии, инструменты и приложения». Hershey, PA: Information Science Reference (2012).

[Flach2008]

Flach, Peter, and Edson Matsubara. «О классификации, ранжировании и оценке вероятностей.» Труды семинара Дагштуля. Замок Дагштуль-Лейбниц-Центр информатики (2008).

3.4.4.19. Отношения правдоподобия классов

The class_likelihood_ratios функция вычисляет положительные и отрицательные отношения правдоподобия \(LR_\pm\) для бинарных классов, что можно интерпретировать как отношение после-тестовых к до-тестовым шансам, как объяснено ниже. Как следствие, эта метрика инвариантна относительно распространенности класса (количество образцов в положительном классе, деленное на общее количество образцов) и может быть экстраполирован между популяциями независимо от возможного дисбаланса классов.

The \(LR_\pm\) Метрики поэтому очень полезны в ситуациях, когда данные, доступные для обучения и оценки классификатора, представляют собой исследуемую популяцию с почти сбалансированными классами, например, в исследовании случай-контроль, в то время как целевое применение, т.е. общая популяция, имеет очень низкую распространённость.

Положительное отношение правдоподобия \(LR_+\) это вероятность того, что классификатор правильно предскажет, что образец принадлежит положительному классу, деленная на вероятность предсказания положительного класса для образца, принадлежащего отрицательному классу:

\[LR_+ = \frac{\text{PR}(P+|T+)}{\text{PR}(P+|T-)}.\]

Обозначение здесь относится к предсказанному (\(P\)) или истинно (\(T\)) метка и знак \(+\) и \(-\) относятся к положительному и отрицательному классам, соответственно, например \(P+\) обозначает "предсказанный положительный".

Аналогично, отрицательное отношение правдоподобия \(LR_-\) это вероятность того, что образец положительного класса будет классифицирован как принадлежащий отрицательному классу, делённая на вероятность того, что образец отрицательного класса будет правильно классифицирован:

\[LR_- = \frac{\text{PR}(P-|T+)}{\text{PR}(P-|T-)}.\]

Для классификаторов выше случайного уровня \(LR_+\) выше 1 чем выше, тем лучше, в то время как \(LR_-\) диапазон от 0 до 1 и чем меньше, тем лучше. Значения \(LR_\pm\approx 1\) соответствуют уровню случайности.

Обратите внимание, что вероятности отличаются от подсчетов, например \(\operatorname{PR}(P+|T+)\) не равно количеству истинно положительных подсчетов tp (см. страница википедии для фактических формул).

Примеры

• Graham Clenaghan

Интерпретация при различной распространенности

Оба отношения правдоподобия классов интерпретируемы через отношение шансов (до и после тестов):

\[\text{post-test odds} = \text{Likelihood ratio} \times \text{pre-test odds}.\]

Шансы в общем случае связаны с вероятностями через

\[\text{odds} = \frac{\text{probability}}{1 - \text{probability}},\]

или эквивалентно

\[\text{probability} = \frac{\text{odds}}{1 + \text{odds}}.\]

Для данной популяции вероятность до теста определяется распространенностью. Путем преобразования шансов в вероятности, отношения правдоподобия могут быть переведены в вероятность истинной принадлежности к любому классу до и после предсказания классификатора:

\[\text{post-test odds} = \text{Likelihood ratio} \times \frac{\text{pre-test probability}}{1 - \text{pre-test probability}},\]

\[\text{post-test probability} = \frac{\text{post-test odds}}{1 + \text{post-test odds}}.\]

Математические дивергенции

Положительное отношение правдоподобия (LR+) не определено, когда \(fp=0\), что означает, что классификатор не ошибочно классифицирует отрицательные метки как положительные. Это условие может указывать либо на идеальное определение всех отрицательных случаев, либо, если также нет истинно положительных предсказаний (\(tp=0\)), что классификатор вообще не предсказывает положительный класс. В первом случае, LR+ может интерпретироваться как np.inf, во втором случае (например, с сильно несбалансированными данными) это может быть интерпретировано как np.nan.

Отрицательное отношение правдоподобия (LR-) не определено, когда \(tn=0\). Такая дивергенция недопустима, так как \(LR_- > 1.0\) будет указывать на увеличение шансов принадлежности образца к положительному классу после классификации как отрицательного, как если бы акт классификации вызвал положительное условие. Это включает случай DummyClassifier которая всегда предсказывает положительный класс (т.е. когда \(tn=fn=0\)).

Оба отношения правдоподобия классов (LR+ and LR-) не определены, когда \(tp=fn=0\), что означает, что в тестовом наборе не было образцов положительного класса. Это может произойти при кросс-валидации на сильно несбалансированных данных и также приводит к делению на ноль.

Если происходит деление на ноль и raise_warning установлено в True (по умолчанию), class_likelihood_ratios вызывает UndefinedMetricWarning и возвращает np.nan по умолчанию, чтобы избежать загрязнения при усреднении по фолдам кросс-валидации. Пользователи могут установить возвращаемые значения в случае деления на ноль с помощью replace_undefined_by параметр.

Для подробной демонстрации class_likelihood_ratios функцию, см. пример ниже.

Ссылки

• Запись в Википедии о отношениях правдоподобия в диагностическом тестировании

• Brenner, H., & Gefeller, O. (1997). Вариация чувствительности, специфичности, отношений правдоподобия и прогностических значений с распространенностью заболевания. Statistics in medicine, 16(9), 981-991.

3.4.4.20. D²-оценка для классификации

Оценка D² вычисляет долю объясненной девиации. Это обобщение R², где квадратичная ошибка обобщена и заменена на выбранную классификационную девиацию \(\text{dev}(y, \hat{y})\) (например, Log loss, Brier score,). D² является формой skill score. Он рассчитывается как

\[D^2(y, \hat{y}) = 1 - \frac{\text{dev}(y, \hat{y})}{\text{dev}(y, y_{\text{null}})} \,.\]

Где \(y_{\text{null}}\) является оптимальным прогнозом модели только с константой (например, доля каждого класса в y_true в случае логарифмической потери и оценки Брайера).

Как и R², наилучший возможный результат равен 1.0, и он может быть отрицательным (поскольку модель может быть сколь угодно хуже). Константная модель, которая всегда предсказывает \(y_{\text{null}}\), игнорируя входные признаки, получит D² оценку 0.0.

Оценка D2 логарифмических потерь

The d2_log_loss_score функция реализует частный случай D² с логарифмическими потерями, см. Логарифмическая потеря, т.е.:

\[\text{dev}(y, \hat{y}) = \text{log_loss}(y, \hat{y}).\]

Вот несколько примеров использования d2_log_loss_score функция:

>>> from sklearn.metrics import d2_log_loss_score
>>> y_true = [1, 1, 2, 3]
>>> y_pred = [
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
... ]
>>> d2_log_loss_score(y_true, y_pred)
0.0
>>> y_true = [1, 2, 3]
>>> y_pred = [
...     [0.98, 0.01, 0.01],
...     [0.01, 0.98, 0.01],
...     [0.01, 0.01, 0.98],
... ]
>>> d2_log_loss_score(y_true, y_pred)
0.981
>>> y_true = [1, 2, 3]
>>> y_pred = [
...     [0.1, 0.6, 0.3],
...     [0.1, 0.6, 0.3],
...     [0.4, 0.5, 0.1],
... ]
>>> d2_log_loss_score(y_true, y_pred)
-0.552

Оценка Брайера D2

The d2_brier_score функция реализует частный случай D² с оценкой Брайера, см. Потеря по шкале Брайера, т.е.:

\[\text{dev}(y, \hat{y}) = \text{brier_score_loss}(y, \hat{y}).\]

Это также называется навыком Брайера (BSS).

Вот несколько примеров использования d2_brier_score функция:

>>> from sklearn.metrics import d2_brier_score
>>> y_true = [1, 1, 2, 3]
>>> y_pred = [
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
...    [0.5, 0.25, 0.25],
... ]
>>> d2_brier_score(y_true, y_pred)
0.0
>>> y_true = [1, 2, 3]
>>> y_pred = [
...    [0.98, 0.01, 0.01],
...    [0.01, 0.98, 0.01],
...    [0.01, 0.01, 0.98],
... ]
>>> d2_brier_score(y_true, y_pred)
0.9991
>>> y_true = [1, 2, 3]
>>> y_pred = [
...    [0.1, 0.6, 0.3],
...    [0.1, 0.6, 0.3],
...    [0.4, 0.5, 0.1],
... ]
>>> d2_brier_score(y_true, y_pred)
-0.370...

3.4.5. Метрики ранжирования для многометочной классификации

В многометочном обучении каждый образец может иметь любое количество истинных меток. Цель — присвоить высокие оценки и лучший ранг истинным меткам.

3.4.5.1. Ошибка покрытия

The coverage_error функция вычисляет среднее количество меток, которые необходимо включить в окончательный прогноз, чтобы все истинные метки были предсказаны. Это полезно, если вы хотите знать, сколько меток с наивысшими оценками вам нужно предсказать в среднем, не пропустив ни одной истинной. Таким образом, лучшее значение этой метрики — это среднее количество истинных меток.

Примечание

Оценка нашей реализации на 1 больше, чем данная в Tsoumakas et al., 2010. Это расширяет её для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.

Формально, задана бинарная индикаторная матрица истинных меток \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) и оценка, связанная с каждой меткой \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\), покрытие определяется как

\[coverage(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \max_{j:y_{ij} = 1} \text{rank}_{ij}\]

с \(\text{rank}_{ij} = \left|\left\{k: \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\right|\). Учитывая определение ранга, совпадения в y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.

Вот небольшой пример использования этой функции:

>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5

3.4.5.2. Средняя точность ранжирования меток

The label_ranking_average_precision_score функция реализует среднюю точность ранжирования меток (LRAP). Эта метрика связана с average_precision_score функция, но основана на понятии ранжирования меток вместо точности и полноты.

Средняя точность ранжирования меток (LRAP) усредняет по образцам ответ на следующий вопрос: для каждой истинной метки, какая доля меток с более высоким рангом была истинными метками? Эта мера производительности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученный результат всегда строго больше 0, а лучшее значение равно 1. Если есть ровно одна релевантная метка на образец, средняя точность ранжирования меток эквивалентна средний обратный ранг.

Формально, задана бинарная индикаторная матрица истинных меток \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) и оценка, связанная с каждой меткой \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\), средняя точность определяется как

\[LRAP(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{||y_i||_0} \sum_{j:y_{ij} = 1} \frac{|\mathcal{L}_{ij}|}{\text{rank}_{ij}}\]

где \(\mathcal{L}_{ij} = \left\{k: y_{ik} = 1, \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\), \(\text{rank}_{ij} = \left|\left\{k: \hat{f}_{ik} \geq \hat{f}_{ij} \right\}\right|\), \(|\cdot|\) вычисляет мощность множества (т.е. количество элементов в множестве), и \(||\cdot||_0\) является \(\ell_0\) “norm” (который вычисляет количество ненулевых элементов в векторе).

Вот небольшой пример использования этой функции:

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score)
0.416

3.4.5.3. Функция потерь для ранжирования

The label_ranking_loss функция вычисляет потерю ранжирования, которая усредняет по выборкам количество пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкий балл, чем ложные метки, взвешенные обратным числом упорядоченных пар ложных и истинных меток. Минимально достижимая потеря ранжирования равна нулю.

Формально, задана бинарная индикаторная матрица истинных меток \(y \in \left\{0, 1\right\}^{n_\text{samples} \times n_\text{labels}}\) и оценка, связанная с каждой меткой \(\hat{f} \in \mathbb{R}^{n_\text{samples} \times n_\text{labels}}\), ранжирующая потеря определяется как

\[ranking\_loss(y, \hat{f}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}} - 1} \frac{1}{||y_i||_0(n_\text{labels} - ||y_i||_0)} \left|\left\{(k, l): \hat{f}_{ik} \leq \hat{f}_{il}, y_{ik} = 1, y_{il} = 0 \right\}\right|\]

где \(|\cdot|\) вычисляет мощность множества (т.е., количество элементов в множестве) и \(||\cdot||_0\) является \(\ell_0\) “norm” (который вычисляет количество ненулевых элементов в векторе).

Вот небольшой пример использования этой функции:

>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score)
0.75
>>> # With the following prediction, we have perfect and minimal loss
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0

Ссылки

• Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Добыча многометочных данных. В Справочнике по добыче данных и обнаружению знаний (стр. 667-685). Springer US.

3.4.5.4. Нормализованный дисконтированный кумулятивный выигрыш

Дисконтированный кумулятивный выигрыш (DCG) и нормализованный дисконтированный кумулятивный выигрыш (NDCG) — это метрики ранжирования, реализованные в dcg_score и ndcg_score ; они сравнивают предсказанный порядок с истинными оценками, такими как релевантность ответов на запрос.

Со страницы Википедии для дисконтированного кумулятивного выигрыша:

“Дисконтированный кумулятивный выигрыш (DCG) — это мера качества ранжирования. В информационном поиске он часто используется для измерения эффективности алгоритмов веб-поисковых систем или связанных приложений. Используя градуированную шкалу релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность, или выигрыш, документа на основе его позиции в списке результатов. Выигрыш накапливается сверху списка результатов донизу, причем выигрыш каждого результата дисконтируется на более низких рангах.”

DCG упорядочивает истинные цели (например, релевантность ответов на запрос) в предсказанном порядке, затем умножает их на логарифмический спад и суммирует результат. Сумма может быть усечена после первых \(K\) результатов, в этом случае мы называем это DCG@K. NDCG, или NDCG@K — это DCG, деленный на DCG, полученный идеальным прогнозом, так что он всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.

По сравнению с функцией потерь ранжирования, NDCG может учитывать оценки релевантности, а не только истинный порядок ранжирования. Поэтому если истинные данные состоят только из упорядочивания, следует предпочесть функцию потерь ранжирования; если истинные данные состоят из фактических оценок полезности (например, 0 для нерелевантных, 1 для релевантных, 2 для очень релевантных), можно использовать NDCG.

Для одного образца, учитывая вектор непрерывных истинных значений для каждой цели \(y \in \mathbb{R}^{M}\), где \(M\) это количество выходов, и предсказание \(\hat{y}\), который индуцирует функцию ранжирования \(f\), оценка DCG равна

\[\sum_{r=1}^{\min(K, M)}\frac{y_{f(r)}}{\log(1 + r)}\]

и оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для \(y\).

Ссылки

• Запись в Википедии о дисконтированном кумулятивном выигрыше

• Jarvelin, K., & Kekalainen, J. (2002). Cumulated gain-based evaluation of IR techniques. ACM Transactions on Information Systems (TOIS), 20(4), 422-446.

• Wang, Y., Wang, L., Li, Y., He, D., Chen, W., & Liu, T. Y. (2013, May). A theoretical analysis of NDCG ranking measures. In Proceedings of the 26th Annual Conference on Learning Theory (COLT 2013)

• McSherry, F., & Najork, M. (2008, March). Computing information retrieval performance measures efficiently in the presence of tied scores. In European conference on information retrieval (pp. 414-421). Springer, Berlin, Heidelberg.

3.4.6. Метрики регрессии

The sklearn.metrics модуль реализует несколько функций потерь, оценок и утилит для измерения производительности регрессии. Некоторые из них были улучшены для обработки многомерного случая: mean_squared_error, mean_absolute_error, r2_score, explained_variance_score, mean_pinball_loss, d2_pinball_score и d2_absolute_error_score.

Эти функции имеют multioutput аргумент ключевого слова, который определяет способ усреднения оценок или потерь для каждой отдельной цели. По умолчанию 'uniform_average', который указывает равномерно взвешенное среднее по выходам. Если ndarray формы (n_outputs,) передаётся, то его элементы интерпретируются как веса, и возвращается соответствующее взвешенное среднее. Если multioutput является 'raw_values', тогда все неизмененные индивидуальные оценки или потери будут возвращены в массиве формы (n_outputs,).

The r2_score и explained_variance_score принимает дополнительное значение 'variance_weighted' для multioutput параметр. Эта опция приводит к взвешиванию каждого отдельного результата по дисперсии соответствующей целевой переменной. Эта настройка количественно оценивает глобально захваченную не масштабированную дисперсию. Если целевые переменные имеют разный масштаб, то этот результат придает больше важности объяснению переменных с более высокой дисперсией.

3.4.6.1. R² оценка, коэффициент детерминации

The r2_score функция вычисляет коэффициент детерминации, обычно обозначается как \(R^2\).

Он представляет долю дисперсии (y), объясненную независимыми переменными в модели. Он дает указание на качество подгонки и, следовательно, меру того, насколько хорошо невидимые образцы могут быть предсказаны моделью через долю объясненной дисперсии.

Поскольку такая дисперсия зависит от набора данных, \(R^2\) может не иметь значимого сравнения между разными наборами данных. Лучший возможный балл - 1.0, и он может быть отрицательным (потому что модель может быть сколь угодно хуже). Постоянная модель, которая всегда предсказывает ожидаемое (среднее) значение y, игнорируя входные признаки, получила бы \(R^2\) оценка 0.0.

Этот пример также будет работать при замене \(R^2\) оценка и Объяснённая дисперсия идентичны.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец и \(y_i\) является соответствующим истинным значением для общего \(n\) образцов, оцененный \(R^2\) определяется как:

\[R^2(y, \hat{y}) = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}\]

где \(\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i\) и \(\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} \epsilon_i^2\).

Обратите внимание, что r2_score вычисляет нескорректированные \(R^2\) без коррекции смещения в выборочной дисперсии y.

В частном случае, когда истинная цель постоянна, \(R^2\) оценка не конечна: она либо NaN (идеальные предсказания) или -Inf (неидеальные предсказания). Такие неконечные оценки могут препятствовать корректной оптимизации модели, такой как перекрестная проверка по сетке. По этой причине поведение по умолчанию r2_score заменить их на 1.0 (идеальные прогнозы) или 0.0 (неидеальные прогнозы). Если force_finite установлено в False, этот показатель возвращается к исходному \(R^2\) определение.

Вот небольшой пример использования r2_score функция:

>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
0.938
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
0.936
>>> r2_score(y_true, y_pred, multioutput='raw_values')
array([0.965, 0.908])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.925
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> r2_score(y_true, y_pred)
1.0
>>> r2_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> r2_score(y_true, y_pred)
0.0
>>> r2_score(y_true, y_pred, force_finite=False)
-inf

Примеры

• См. Модели на основе L1 для разреженных сигналов для примера использования оценки R² для оценки Lasso и Elastic Net на разреженных сигналах.

3.4.6.2. Средняя абсолютная ошибка

The mean_absolute_error функция вычисляет средняя абсолютная ошибка, метрика риска, соответствующая ожидаемому значению функции потерь абсолютной ошибки или \(l1\)-норма потерь.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец, и \(y_i\) является соответствующим истинным значением, тогда средняя абсолютная ошибка (MAE), оцененная по \(n_{\text{samples}}\) определяется как

\[\text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|.\]

Вот небольшой пример использования mean_absolute_error функция:

>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.85

3.4.6.3. Среднеквадратичная ошибка

The mean_squared_error функция вычисляет среднеквадратическая ошибка, метрика риска, соответствующая ожидаемому значению квадратичной ошибки или потери.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец, и \(y_i\) является соответствующим истинным значением, тогда среднеквадратичная ошибка (MSE), оцененная по \(n_{\text{samples}}\) определяется как

\[\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2.\]

Вот небольшой пример использования mean_squared_error функция:

>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083

Примеры

• См. Градиентный бустинг для регрессии для примера использования среднеквадратичной ошибки для оценки градиентного бустинга регрессии.

Извлечение квадратного корня из MSE, называемое среднеквадратичной ошибкой (RMSE), является еще одной распространенной метрикой, которая дает меру в тех же единицах, что и целевая переменная. RMSE доступна через root_mean_squared_error функция.

3.4.6.4. Средняя квадратичная логарифмическая ошибка

The mean_squared_log_error функция вычисляет метрику риска, соответствующую ожидаемому значению квадратичной логарифмической ошибки или потери.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец, и \(y_i\) является соответствующим истинным значением, тогда средняя квадратичная логарифмическая ошибка (MSLE), оцененная по \(n_{\text{samples}}\) определяется как

\[\text{MSLE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} (\log_e (1 + y_i) - \log_e (1 + \hat{y}_i) )^2.\]

Где \(\log_e (x)\) означает натуральный логарифм от \(x\). Эта метрика лучше всего подходит для использования, когда цели имеют экспоненциальный рост, например, количество населения, средние продажи товара за несколько лет и т.д. Обратите внимание, что эта метрика штрафует заниженную оценку сильнее, чем завышенную.

Вот небольшой пример использования mean_squared_log_error функция:

>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.0397
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)
0.044

Среднеквадратичная логарифмическая ошибка (RMSLE) доступна через root_mean_squared_log_error функция.

3.4.6.5. Средняя абсолютная процентная ошибка

The mean_absolute_percentage_error (MAPE), также известная как средняя абсолютная процентная ошибка (MAPD), является метрикой оценки для задач регрессии. Идея этой метрики заключается в чувствительности к относительным ошибкам. Например, она не изменяется при глобальном масштабировании целевой переменной.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец и \(y_i\) является соответствующим истинным значением, тогда средняя абсолютная процентная ошибка (MAPE), оцененная по \(n_{\text{samples}}\) определяется как

\[\text{MAPE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \frac{{}\left| y_i - \hat{y}_i \right|}{\max(\epsilon, \left| y_i \right|)}\]

где \(\epsilon\) — это произвольное малое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равен нулю.

The mean_absolute_percentage_error функция поддерживает многомерный вывод.

Вот небольшой пример использования mean_absolute_percentage_error функция:

>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666

В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы игнорировал значения малой величины и отражал только ошибку предсказания наибольшего значения. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку относительно фактического выхода.

Примечание

Формула MAPE здесь не представляет общепринятое определение «процентного»: процент в диапазоне [0, 100] преобразуется в относительное значение в диапазоне [0, 1] путем деления на 100. Таким образом, ошибка в 200% соответствует относительной ошибке 2. Мотивация здесь заключается в том, чтобы иметь диапазон значений, более согласованный с другими метриками ошибок в scikit-learn, такими как accuracy_score.

Чтобы получить среднюю абсолютную процентную ошибку в соответствии с формулой из Википедии, умножьте mean_absolute_percentage_error вычисленное здесь на 100.

Ссылки

• Запись в Википедии для средней абсолютной процентной ошибки

3.4.6.6. Средняя абсолютная ошибка

The median_absolute_error особенно интересен, поскольку он устойчив к выбросам. Потери рассчитываются путем взятия медианы всех абсолютных разностей между целевым значением и прогнозом.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец и \(y_i\) является соответствующим истинным значением, тогда медианная абсолютная ошибка (MedAE), оцененная по \(n_{\text{samples}}\) определяется как

\[\text{MedAE}(y, \hat{y}) = \text{median}(\mid y_1 - \hat{y}_1 \mid, \ldots, \mid y_n - \hat{y}_n \mid).\]

The median_absolute_error не поддерживает многомерный вывод.

Вот небольшой пример использования median_absolute_error функция:

>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5

3.4.6.7. Проекция на одну компоненту и предсказательная сила

The max_error функция вычисляет максимум остаточная ошибка , метрика, которая фиксирует наихудшую ошибку между предсказанным значением и истинным значением. В идеально обученной модели регрессии с одним выходом, max_error будет 0 на обучающем наборе, и хотя это было бы крайне маловероятно в реальном мире, эта метрика показывает степень ошибки, которую модель имела при обучении.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец, и \(y_i\) является соответствующим истинным значением, тогда максимальная ошибка определяется как

\[\text{Max Error}(y, \hat{y}) = \max(| y_i - \hat{y}_i |)\]

Вот небольшой пример использования max_error функция:

>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6.0

The max_error не поддерживает многомерный вывод.

3.4.6.8. Объяснённая дисперсия

The explained_variance_score вычисляет объяснённая дисперсия оценка регрессии.

Если \(\hat{y}\) является оценённым целевым выходом, \(y\) соответствующий (правильный) целевой вывод, и \(Var\) является Дисперсия, квадрат стандартного отклонения, тогда объясненная дисперсия оценивается следующим образом:

\[explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}}\]

Наилучший возможный результат - 1.0, меньшие значения хуже.

Ссылка на R² оценка, коэффициент детерминации

Разница между оценкой объяснённой дисперсии и R² оценка, коэффициент детерминации что оценка объясненной дисперсии не учитывает систематическое смещение в предсказании. По этой причине, R² оценка, коэффициент детерминации обычно следует предпочитать.

В частном случае, когда истинная цель постоянна, оценка объясненной дисперсии не конечна: она либо NaN (идеальные предсказания) или -Inf (неидеальные предсказания). Такие неконечные оценки могут препятствовать корректной оптимизации модели, такой как кросс-валидация с поиском по сетке. По этой причине поведение по умолчанию explained_variance_score заменить их на 1.0 (идеальные предсказания) или 0.0 (неидеальные предсказания). Вы можете установить force_finite параметр для False чтобы предотвратить это исправление и вернуться к исходной оценке объясненной дисперсии.

Вот небольшой пример использования explained_variance_score функция:

>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
array([0.967, 1.        ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.990
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> explained_variance_score(y_true, y_pred)
1.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> explained_variance_score(y_true, y_pred)
0.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
-inf

3.4.6.9. Средние девиансы Пуассона, Гамма и Твиди

The mean_tweedie_deviance функция вычисляет средняя ошибка отклонения Твиди с power параметр (\(p\)). Это метрика, которая выявляет предсказанные ожидаемые значения целей регрессии.

Существуют следующие особые случаи,

• когда power=0 это эквивалентно mean_squared_error.

• когда power=1 это эквивалентно mean_poisson_deviance.

• когда power=2 это эквивалентно mean_gamma_deviance.

Если \(\hat{y}_i\) это предсказанное значение \(i\)-й образец, и \(y_i\) является соответствующим истинным значением, тогда средняя ошибка отклонения Твиди (D) для степени \(p\), оценено по \(n_{\text{samples}}\) определяется как

\[\begin{split}\text{D}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum_{i=0}^{n_\text{samples} - 1} \begin{cases} (y_i-\hat{y}_i)^2, & \text{for }p=0\text{ (Normal)}\\ 2(y_i \log(y_i/\hat{y}_i) + \hat{y}_i - y_i), & \text{for }p=1\text{ (Poisson)}\\ 2(\log(\hat{y}_i/y_i) + y_i/\hat{y}_i - 1), & \text{for }p=2\text{ (Gamma)}\\ 2\left(\frac{\max(y_i,0)^{2-p}}{(1-p)(2-p)}- \frac{y_i\,\hat{y}_i^{1-p}}{1-p}+\frac{\hat{y}_i^{2-p}}{2-p}\right), & \text{otherwise} \end{cases}\end{split}\]

Дисперсия Твиди является однородной функцией степени 2-power. Таким образом, гамма-распределение с power=2 означает, что одновременное масштабирование y_true и y_pred не влияет на девианс. Для распределения Пуассона power=1 девианс масштабируется линейно, а для нормального распределения (power=0), квадратично. В общем, чем выше power тем меньший вес придаётся экстремальным отклонениям между истинными и предсказанными целями.

Например, сравним два прогноза 1.5 и 150, которые оба на 50% больше соответствующих истинных значений.

Среднеквадратичная ошибка (power=0) очень чувствительна к разнице предсказаний второй точки:

>>> from sklearn.metrics import mean_tweedie_deviance
>>> mean_tweedie_deviance([1.0], [1.5], power=0)
0.25
>>> mean_tweedie_deviance([100.], [150.], power=0)
2500.0

Если мы увеличим power до 1,:

>>> mean_tweedie_deviance([1.0], [1.5], power=1)
0.189
>>> mean_tweedie_deviance([100.], [150.], power=1)
18.9

разница в ошибках уменьшается. Наконец, установив, power=2:

>>> mean_tweedie_deviance([1.0], [1.5], power=2)
0.144
>>> mean_tweedie_deviance([100.], [150.], power=2)
0.144

мы получили бы идентичные ошибки. Девнанс, когда power=2 поэтому чувствительно только к относительным ошибкам.

3.4.6.10. Потери Pinball

The mean_pinball_loss функция используется для оценки прогностической производительности квантильная регрессия модели.

\[\text{pinball}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} \alpha \max(y_i - \hat{y}_i, 0) + (1 - \alpha) \max(\hat{y}_i - y_i, 0)\]

Значение потерь pinball эквивалентно половине mean_absolute_error когда параметр квантиля alpha установлено в 0.5.

Вот небольшой пример использования mean_pinball_loss функция:

>>> from sklearn.metrics import mean_pinball_loss
>>> y_true = [1, 2, 3]
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1)
0.033
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1)
0.3
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9)
0.3
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9)
0.033
>>> mean_pinball_loss(y_true, y_true, alpha=0.1)
0.0
>>> mean_pinball_loss(y_true, y_true, alpha=0.9)
0.0

Возможно построить объект scorer с конкретным выбором alpha:

>>> from sklearn.metrics import make_scorer
>>> mean_pinball_loss_95p = make_scorer(mean_pinball_loss, alpha=0.95)

Такой скорер может использоваться для оценки обобщающей способности квантильного регрессора с помощью кросс-валидации:

>>> from sklearn.datasets import make_regression
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.ensemble import GradientBoostingRegressor
>>>
>>> X, y = make_regression(n_samples=100, random_state=0)
>>> estimator = GradientBoostingRegressor(
...     loss="quantile",
...     alpha=0.95,
...     random_state=0,
... )
>>> cross_val_score(estimator, X, y, cv=5, scoring=mean_pinball_loss_95p)
array([13.6, 9.7, 23.3, 9.5, 10.4])

Также возможно создание объектов scorer для настройки гиперпараметров. Знак потерь должен быть изменён, чтобы обеспечить, что большее значение означает лучшее, как объяснено в примере ниже.

Примеры

• См. Интервалы прогнозирования для регрессии градиентного бустинга для примера использования потерь пинбола для оценки и настройки гиперпараметров моделей квантильной регрессии на данных с несимметричным шумом и выбросами.

3.4.6.11. Оценка D²

Оценка D² вычисляет долю объясненной девиации. Это обобщение R², где квадратичная ошибка обобщена и заменена на выбранную девиацию \(\text{dev}(y, \hat{y})\) (например, Tweedie, pinball или средняя абсолютная ошибка). D² является формой skill score. Он рассчитывается как

\[D^2(y, \hat{y}) = 1 - \frac{\text{dev}(y, \hat{y})}{\text{dev}(y, y_{\text{null}})} \,.\]

Где \(y_{\text{null}}\) является оптимальным прогнозом модели только с пересечением (например, среднее значение y_true для случая Tweedie, медиана для абсолютной ошибки и альфа-квантиль для потерь pinball).

Как и R², наилучший возможный результат равен 1.0, и он может быть отрицательным (поскольку модель может быть сколь угодно хуже). Константная модель, которая всегда предсказывает \(y_{\text{null}}\), игнорируя входные признаки, получит D² оценку 0.0.

Оценка D² Твиди

The d2_tweedie_score функция реализует частный случай D² где \(\text{dev}(y, \hat{y})\) является отклонением Твиди, см. Средние девиансы Пуассона, Гамма и Твиди. Также известен как D² Tweedie и связан с индексом отношения правдоподобия Макфаддена.

Аргумент power определяет степень Твиди как для mean_tweedie_deviance. Обратите внимание, что для power=0, d2_tweedie_score равно r2_score (для одиночных целей).

Объект оценщика с конкретным выбором power может быть построен:

>>> from sklearn.metrics import d2_tweedie_score, make_scorer
>>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5)

D² pinball score

The d2_pinball_score функция реализует частный случай D² с функцией потерь pinball, см. Потери Pinball, т.е.:

\[\text{dev}(y, \hat{y}) = \text{pinball}(y, \hat{y}).\]

Аргумент alpha определяет наклон потерь пинболла как для mean_pinball_loss (Потери Pinball). Он определяет уровень квантиля alpha для которых функция потерь пинбола и также D² оптимальны. Обратите внимание, что для alpha=0.5 (по умолчанию) d2_pinball_score равно d2_absolute_error_score.

Объект оценщика с конкретным выбором alpha может быть построен:

>>> from sklearn.metrics import d2_pinball_score, make_scorer
>>> d2_pinball_score_08 = make_scorer(d2_pinball_score, alpha=0.8)

Оценка абсолютной ошибки D²

The d2_absolute_error_score функция реализует частный случай Средняя абсолютная ошибка:

\[\text{dev}(y, \hat{y}) = \text{MAE}(y, \hat{y}).\]

Вот несколько примеров использования d2_absolute_error_score функция:

>>> from sklearn.metrics import d2_absolute_error_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> d2_absolute_error_score(y_true, y_pred)
0.764
>>> y_true = [1, 2, 3]
>>> y_pred = [1, 2, 3]
>>> d2_absolute_error_score(y_true, y_pred)
1.0
>>> y_true = [1, 2, 3]
>>> y_pred = [2, 2, 2]
>>> d2_absolute_error_score(y_true, y_pred)
0.0

3.4.6.12. Визуальная оценка моделей регрессии

Среди методов оценки качества регрессионных моделей scikit-learn предоставляет PredictionErrorDisplay класс. Он позволяет визуально проверить ошибки предсказания модели двумя разными способами.

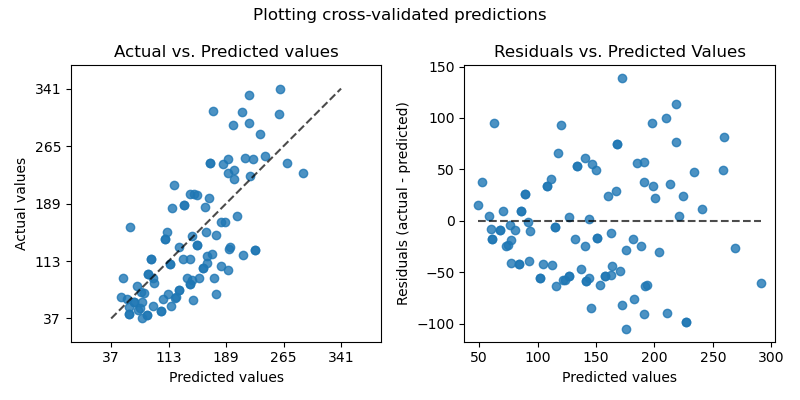
График слева показывает фактические значения против предсказанных значений. Для задачи регрессии без шума, направленной на предсказание (условного) математического ожидания y, идеальная регрессионная модель отображала бы точки данных на диагонали, определяемой предсказанными значениями, равными фактическим. Чем дальше от этой оптимальной линии, тем больше ошибка модели. В более реалистичной ситуации с неустранимым шумом, то есть когда не все вариации y может быть объяснено признаками в X, then the best model would lead to a cloud of points densely arranged around the diagonal.

Обратите внимание, что вышесказанное верно только тогда, когда предсказанные значения являются ожидаемым значением y задан X. Это обычно относится к моделям регрессии, которые минимизируют целевую функцию среднеквадратичной ошибки или, в более общем случае, среднее отклонение Tweedie для любого значения его параметра "power".

При построении прогнозов оценщика, который предсказывает квантиль для y задан X, например, QuantileRegressor или любой другой модели, минимизирующей потери пинболлаожидается, что часть точек будет лежать выше или ниже диагонали в зависимости от оцениваемого уровня квантиля.

В целом, хотя этот график интуитивно понятен для чтения, он не очень информирует нас о том, что делать для получения лучшей модели.

Правый график показывает остатки (т.е. разницу между фактическими и предсказанными значениями) в зависимости от предсказанных значений.

Этот график позволяет легче визуализировать, следуют ли остатки и гомоскедастичный или гетероскедастичный распределение.

В частности, если истинное распределение y|X распределен по Пуассону или Гамме, ожидается, что дисперсия остатков оптимальной модели будет расти с предсказанным значением E[y|X] (либо линейно для Пуассона, либо квадратично для Гаммы).

При обучении модели линейной регрессии методом наименьших квадратов (см. LinearRegression и Ridge), мы можем использовать этот график для проверки, не являются ли некоторые из предположения модели выполнены, в частности, что остатки должны быть некоррелированы, их ожидаемое значение должно быть нулевым и их дисперсия должна быть постоянной (гомоскедастичность).

Если это не так, и в частности, если график остатков показывает некоторую структуру в форме банана, это указывает на то, что модель, вероятно, неправильно специфицирована, и что нелинейное преобразование признаков или переход к нелинейной регрессионной модели может быть полезным.

Обратитесь к примеру ниже, чтобы увидеть оценку модели, использующую это отображение.

Примеры

• См. Эффект преобразования целей в регрессионной модели для примера использования PredictionErrorDisplay для визуализации улучшения качества предсказания регрессионной модели, полученного путём преобразования целевой переменной перед обучением.

3.4.7. Метрики кластеризации

The sklearn.metrics модуль реализует несколько функций потерь, оценок и утилит для измерения производительности кластеризации. Для получения дополнительной информации см. Оценка производительности кластеризации раздел для кластеризации экземпляров, и Оценка бикластеризации для бикластеризации.

3.4.8. Фиктивные оценки

При проведении обучения с учителем простой проверкой здравомыслия является сравнение своего оценщика с простыми эмпирическими правилами. DummyClassifier реализует несколько таких простых стратегий для классификации:

• stratified генерирует случайные предсказания, учитывая распределение классов обучающего набора.

• most_frequent всегда предсказывает наиболее частую метку в обучающем наборе.

• prior всегда предсказывает класс, который максимизирует априорную вероятность класса (как most_frequent) и predict_proba возвращает априорную вероятность класса.

• uniform генерирует прогнозы равномерно случайным образом.

• constant всегда предсказывает постоянную метку, предоставленную пользователем.

  Основная мотивация этого метода — F1-оценка, когда положительный класс находится в меньшинстве.

рассматривается как положительный класс. predict метод полностью игнорирует входные данные!

Для иллюстрации DummyClassifier, сначала создадим несбалансированный набор данных:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

Далее сравним точность SVC и most_frequent:

>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.63
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)
0.579

Мы видим, что SVC не работает намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:

>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.94

Мы видим, что точность повысилась почти до 100%. Стратегия перекрестной проверки рекомендуется для лучшей оценки точности, если это не слишком затратно по CPU. Для получения дополнительной информации см. Кросс-валидация: оценка производительности оценщика раздел. Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; см. Настройка гиперпараметров оценщика раздел для подробностей.

В более общем случае, когда точность классификатора слишком близка к случайной, это вероятно означает, что что-то пошло не так: признаки не полезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т.д.

DummyRegressor также реализует четыре простых эмпирических правила для регрессии:

• mean всегда предсказывает среднее значение целевых переменных обучения.

• median всегда предсказывает медиану целевых значений обучающей выборки.

• quantile всегда предсказывает предоставленный пользователем квантиль целевых значений обучения.

• constant всегда предсказывает постоянное значение, предоставленное пользователем.

Во всех этих стратегиях predict метод полностью игнорирует входные данные.