1.11. Ансамбли: градиентный бустинг, случайные леса, бэггинг, голосование, стэкинг#
Ансамблевые методы объединить предсказания нескольких базовых оценщиков, построенных с использованием заданного алгоритма обучения, чтобы улучшить обобщаемость / устойчивость по сравнению с одним оценщиком.
Два очень известных примера методов ансамблей - это градиентно-бустированные деревья и случайные леса.
В более общем случае, ансамблевые модели могут применяться к любому базовому алгоритму, помимо деревьев, в методах усреднения, таких как Методы бэггинга, стэкинг моделей, или Голосование, или в бустинге, как AdaBoost.
1.11.1. Градиентный бустинг деревьев#
Градиентный бустинг деревьев или градиентный бустинг деревьев решений (GBDT) является обобщением бустинга на произвольные дифференцируемые функции потерь, см. основополагающую работу [Friedman2001]. GBDT — отличная модель как для регрессии, так и для классификации, особенно для табличных данных.
1.11.1.1. Градиентный бустинг на основе гистограмм#
Scikit-learn 0.21 представил две новые реализации градиентного бустинга деревьев, а именно HistGradientBoostingClassifier
и HistGradientBoostingRegressor, вдохновленный
LightGBM (См. [LightGBM]).
Эти оценщики на основе гистограмм могут быть на порядки быстрее
чем GradientBoostingClassifier и
GradientBoostingRegressor когда количество выборок больше десятков тысяч выборок.
Они также имеют встроенную поддержку пропущенных значений, что позволяет избежать необходимости в импьютере.
Эти быстрые оценщики сначала группируют входные выборки X в целочисленные бины (обычно 256 бинов), что значительно сокращает количество рассматриваемых точек разбиения и позволяет алгоритму использовать целочисленные структуры данных (гистограммы) вместо отсортированных непрерывных значений при построении деревьев. API этих оценщиков немного отличается, и некоторые функции из
GradientBoostingClassifier и GradientBoostingRegressor
еще не поддерживаются, например, некоторые функции потерь.
Примеры
Графики частичной зависимости и индивидуального условного ожидания
Сравнение моделей случайных лесов и градиентного бустинга на гистограммах
1.11.1.1.1. Использование#
Большинство параметров не изменились по сравнению с
GradientBoostingClassifier и GradientBoostingRegressor.
Одно исключение - это max_iter параметр, который заменяет n_estimators, и
управляет количеством итераций процесса бустинга:
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> from sklearn.datasets import make_hastie_10_2
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = HistGradientBoostingClassifier(max_iter=100).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.8965
Доступные потери для регрессия являются:
'squared_error', который является функцией потерь по умолчанию;
'absolute_error', который менее чувствителен к выбросам, чем квадратичная ошибка;
‘gamma’, который хорошо подходит для моделирования строго положительных исходов;
‘poisson’, который хорошо подходит для моделирования подсчетов и частот;
'quantile', который позволяет оценить условный квантиль, который позже можно использовать для получения интервалов прогнозирования.
Для классификация, 'log_loss' - единственный вариант. Для бинарной классификации
используется бинарная лог-потеря, также известная как биномиальное отклонение или бинарная
кросс-энтропия. Для n_classes >= 3, он использует функцию многоклассовых логарифмических потерь,
с мультиномиальным отклонением и категориальной кросс-энтропией как альтернативными названиями.
Соответствующая версия потерь выбирается на основе y передано в
fit.
Размер деревьев может контролироваться через max_leaf_nodes,
max_depth, и min_samples_leaf параметры.
Количество бинов, используемых для бинирования данных, контролируется с помощью max_bins
параметр. Использование меньшего количества бинов действует как форма регуляризации. Обычно рекомендуется использовать как можно больше бинов (255), что является значением по умолчанию.
The l2_regularization параметр действует как регуляризатор для функции потерь и соответствует \(\lambda\) в следующем выражении (см. уравнение (2)
в [XGBoost]):
Подробности о l2-регуляризации#
Важно заметить, что член потерь \(l(\hat{y}_i, y_i)\) описывает только половину фактической функции потерь, за исключением потери пинбола и абсолютной ошибки.
Индекс \(k\) относится к k-му дереву в ансамбле деревьев. В случае регрессии и бинарной классификации модели градиентного бустинга выращивают одно дерево за итерацию, затем \(k\) работает до max_iter. В случае многоклассовых задач классификации максимальное значение индекса \(k\) является
n_classes \(\times\) max_iter.
Если \(T_k\) обозначает количество листьев в k-м дереве, тогда \(w_k\)
является вектором длины \(T_k\), который содержит значения листьев вида w
= -sum_gradient / (sum_hessian + l2_regularization) (см. уравнение (5) в
[XGBoost]).
Значения листьев \(w_k\) получаются путем деления суммы градиентов функции потерь на суммарную сумму гессианов. Добавление регуляризации к знаменателю штрафует листья с малыми гессианами (плоские области), приводя к меньшим обновлениям. Эти \(w_k\) значения затем вносят вклад в прогноз модели для данного входа, который попадает в соответствующий лист. Окончательный прогноз представляет собой сумму базового прогноза и вкладов от каждого дерева. Результат этой суммы затем преобразуется обратной функцией связи в зависимости от выбора функции потерь (см. Математическая формулировка).
Обратите внимание, что оригинальная статья [XGBoost] вводит термин \(\gamma\sum_k
T_k\) который штрафует количество листьев (делая его сглаженной версией
max_leaf_nodes), не представленный здесь, так как не реализован в scikit-learn;
тогда как \(\lambda\) штрафует величину индивидуальных предсказаний дерева
перед масштабированием с помощью скорости обучения, см.
Сжатие через скорость обучения.
Обратите внимание, что ранняя остановка включена по умолчанию, если количество выборок больше 10,000. Поведение ранней остановки контролируется через
early_stopping, scoring, validation_fraction,
n_iter_no_change, и tol параметры. Можно досрочно остановиться
используя произвольный scorer, или только потери на обучении или валидации.
Обратите внимание, что по техническим причинам использование вызываемого объекта в качестве скорера значительно медленнее,
чем использование потерь. По умолчанию ранняя остановка выполняется, если в обучающем наборе
не менее 10 000 образцов, с использованием потерь на валидации.
1.11.1.1.2. Поддержка пропущенных значений#
HistGradientBoostingClassifier и
HistGradientBoostingRegressor имеют встроенную поддержку пропущенных
значений (NaN).
Во время обучения построитель дерева узнает на каждой точке разделения, должны ли образцы с пропущенными значениями идти в левый или правый дочерний узел, на основе потенциального выигрыша. При прогнозировании образцы с пропущенными значениями назначаются левому или правому дочернему узлу соответственно:
>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> import numpy as np
>>> X = np.array([0, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 0, 1, 1])
Когда паттерн пропущенных значений является предсказательным, разделение может выполняться на основе того, пропущено ли значение признака или нет:
>>> X = np.array([0, np.nan, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 1, 0, 0, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1,
... max_depth=2,
... learning_rate=1,
... max_iter=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 1, 0, 0, 1])
Если во время обучения для данного признака не было обнаружено пропущенных значений, то образцы с пропущенными значениями сопоставляются с тем дочерним узлом, который имеет наибольшее количество образцов.
Примеры
1.11.1.1.3. Поддержка весов образцов#
HistGradientBoostingClassifier и
HistGradientBoostingRegressor поддерживать веса образцов во время
fit.
Следующий игрушечный пример демонстрирует, что образцы с весом образца, равным нулю, игнорируются:
>>> X = [[1, 0],
... [1, 0],
... [1, 0],
... [0, 1]]
>>> y = [0, 0, 1, 0]
>>> # ignore the first 2 training samples by setting their weight to 0
>>> sample_weight = [0, 0, 1, 1]
>>> gb = HistGradientBoostingClassifier(min_samples_leaf=1)
>>> gb.fit(X, y, sample_weight=sample_weight)
HistGradientBoostingClassifier(...)
>>> gb.predict([[1, 0]])
array([1])
>>> gb.predict_proba([[1, 0]])[0, 1]
np.float64(0.999)
Как вы можете видеть, [1, 0] удобно классифицируется как 1 поскольку первые
две выборки игнорируются из-за их весов выборок.
Деталь реализации: учет весов выборок эквивалентен умножению градиентов (и гессианов) на веса выборок. Обратите внимание, что этап бининга (в частности, вычисление квантилей) не учитывает веса.
1.11.1.1.4. Поддержка категориальных признаков#
HistGradientBoostingClassifier и
HistGradientBoostingRegressor имеют встроенную поддержку категориальных
признаков: они могут рассматривать разделения на неупорядоченные, категориальные данные.
Для наборов данных с категориальными признаками использование нативной поддержки категориальных признаков часто лучше, чем полагаться на one-hot кодирование (OneHotEncoder), потому что one-hot кодирование требует большей глубины дерева для достижения эквивалентных разбиений. Также обычно лучше полагаться на встроенную поддержку категориальных признаков, чем рассматривать категориальные признаки как непрерывные (порядковые), что происходит для порядково закодированных категориальных данных, поскольку категории являются номинальными величинами, где порядок не имеет значения.
Для включения поддержки категориальных признаков можно передать булевую маску в
categorical_features параметр, указывающий, какой признак категориальный. В
следующем примере первый признак будет обрабатываться как категориальный, а
второй признак как числовой:
>>> gbdt = HistGradientBoostingClassifier(categorical_features=[True, False])
Эквивалентно, можно передать список целых чисел, указывающих индексы категориальных признаков:
>>> gbdt = HistGradientBoostingClassifier(categorical_features=[0])
Когда входные данные — DataFrame, также можно передать список имен столбцов:
>>> gbdt = HistGradientBoostingClassifier(categorical_features=["site", "manufacturer"])
Наконец, когда входные данные представлены в виде DataFrame, мы можем использовать
categorical_features="from_dtype" в этом случае все столбцы с категориальным
dtype будут рассматриваться как категориальные признаки.
Мощность каждого категориального признака должна быть меньше max_bins
параметр. Пример использования градиентного бустинга на основе гистограмм с категориальными признаками см. в
Поддержка категориальных признаков в градиентном бустинге.
Если во время обучения присутствуют пропущенные значения, они будут обрабатываться как отдельная категория. Если во время обучения пропущенных значений нет, то во время предсказания пропущенные значения сопоставляются с дочерним узлом, содержащим наибольшее количество образцов (как и для непрерывных признаков). При предсказании категории, которые не встречались во время обучения, будут обрабатываться как пропущенные значения.
Поиск разбиений с категориальными признаками#
Канонический способ рассмотрения категориальных разбиений в дереве — рассмотреть
все \(2^{K - 1} - 1\) partitions, where \(K\) — это количество категорий. Это может быстро стать неподъёмным, когда \(K\) велик.
К счастью, поскольку деревья градиентного бустинга всегда являются деревьями регрессии (даже для задач классификации), существует более быстрая стратегия, которая может дать эквивалентные разбиения. Сначала категории признака сортируются по дисперсии целевой переменной для каждой категории k. После сортировки категорий можно рассматривать непрерывные разбиения, т.е. рассматривать категории
как если бы они были упорядоченными непрерывными значениями (см. Fisher [Fisher1958] для
формального доказательства). В результате только \(K - 1\) разделения должны рассматриваться вместо \(2^{K - 1} - 1\). Начальная сортировка является
\(\mathcal{O}(K \log(K))\) операции, что приводит к общей сложности
\(\mathcal{O}(K \log(K) + K)\), вместо \(\mathcal{O}(2^K)\).
Примеры
1.11.1.1.5. Монотонные ограничения#
В зависимости от задачи, у вас может быть априорное знание, указывающее, что данный признак в целом должен оказывать положительное (или отрицательное) влияние на целевую переменную. Например, при прочих равных, более высокий кредитный рейтинг должен увеличивать вероятность одобрения кредита. Монотонные ограничения позволяют включить такое априорное знание в модель.
Для предиктора \(F\) с двумя признаками:
a ограничение монотонного возрастания является ограничением вида:
\[x_1 \leq x_1' \implies F(x_1, x_2) \leq F(x_1', x_2)\]a ограничение монотонного убывания является ограничением вида:
\[x_1 \leq x_1' \implies F(x_1, x_2) \geq F(x_1', x_2)\]
Вы можете задать монотонное ограничение для каждого признака с помощью
monotonic_cst параметр. Для каждого признака значение 0 указывает на отсутствие
ограничения, а 1 и -1 указывают на монотонное увеличение и
монотонное уменьшение ограничения соответственно:
>>> from sklearn.ensemble import HistGradientBoostingRegressor
... # monotonic increase, monotonic decrease, and no constraint on the 3 features
>>> gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1, 0])
В контексте бинарной классификации наложение ограничения монотонного увеличения (уменьшения) означает, что более высокие значения признака должны оказывать положительное (отрицательное) влияние на вероятность принадлежности образцов к положительному классу.
Тем не менее, монотонные ограничения лишь незначительно ограничивают влияние признаков на выход. Например, ограничения монотонного возрастания и убывания не могут быть использованы для обеспечения следующего ограничения моделирования:
Кроме того, монотонные ограничения не поддерживаются для многоклассовой классификации.
Для практической реализации монотонных ограничений с градиентным бустингом на основе гистограмм, включая то, как они могут улучшить обобщение при наличии предметных знаний, см. Монотонные ограничения.
Примечание
Поскольку категории являются неупорядоченными величинами, невозможно наложить монотонные ограничения на категориальные признаки.
Примеры
1.11.1.1.6. Ограничения взаимодействий#
Априори, градиентные бустинговые деревья с гистограммами могут использовать любой признак для разделения узла на дочерние узлы. Это создает так называемые взаимодействия между признаками, т.е. использование разных признаков в качестве разделителей вдоль ветви. Иногда требуется ограничить возможные взаимодействия, см. [Mayer2022]. Это можно сделать с помощью параметра interaction_cst, где можно указать индексы
признаков, которым разрешено взаимодействовать.
Например, с 3 признаками в общей сложности, interaction_cst=[{0}, {1}, {2}]
запрещает все взаимодействия.
Ограничения [{0, 1}, {1, 2}] указать две группы потенциально
взаимодействующих признаков. Признаки 0 и 1 могут взаимодействовать друг с другом, как и
признаки 1 и 2. Но обратите внимание, что признаки 0 и 2 не могут взаимодействовать.
Ниже показано дерево и возможные разбиения дерева:
1 <- Both constraint groups could be applied from now on
/ \
1 2 <- Left split still fulfills both constraint groups.
/ \ / \ Right split at feature 2 has only group {1, 2} from now on.
LightGBM использует ту же логику для перекрывающихся групп.
Обратите внимание, что функции, не перечисленные в interaction_cst автоматически
назначаются в группу взаимодействия сами себе. Снова с 3 признаками это
означает, что [{0}] эквивалентно [{0}, {1, 2}].
Примеры
Ссылки
M. Mayer, S.C. Bourassa, M. Hoesli, and D.F. Scognamiglio. 2022. Приложения машинного обучения к оценке земли и сооружений. Journal of Risk and Financial Management 15, no. 5: 193
1.11.1.1.7. Низкоуровневый параллелизм#
HistGradientBoostingClassifier и
HistGradientBoostingRegressor используйте OpenMP
для распараллеливания через Cython. Для получения дополнительной информации о том, как управлять
количеством потоков, обратитесь к нашей Параллелизм примечания.
Следующие части распараллеливаются:
отображение выборок из реальных значений в целочисленные бины (однако поиск порогов бинов является последовательным)
построение гистограмм распараллелено по признакам
поиск наилучшей точки разделения в узле распараллеливается по признакам
во время подгонки, отображение образцов в левые и правые дочерние узлы распараллеливается по образцам
вычисления градиента и гессиана распараллеливаются по выборкам
предсказание распараллеливается по образцам
1.11.1.1.8. Почему это быстрее#
Узким местом процедуры градиентного бустинга является построение деревьев
решений. Построение традиционного дерева решений (как в других GBDT
GradientBoostingClassifier и GradientBoostingRegressor)
требует сортировки выборок в каждом узле (для
каждой характеристики). Сортировка необходима для того, чтобы потенциальный выигрыш от точки разделения
мог быть вычислен эффективно. Разделение одного узла имеет, таким образом, сложность
\(\mathcal{O}(n_\text{features} \times n \log(n))\) где \(n\)
— это количество выборок в узле.
HistGradientBoostingClassifier и
HistGradientBoostingRegressor, в отличие от них, не требуют сортировки значений признаков и вместо этого используют структуру данных, называемую гистограммой, где образцы неявно упорядочены. Построение гистограммы имеет
\(\mathcal{O}(n)\) сложность, поэтому процедура разделения узла имеет
\(\mathcal{O}(n_\text{features} \times n)\) сложность, значительно меньшая,
чем предыдущая. Кроме того, вместо рассмотрения \(n\) точки разделения, мы рассматриваем только max_bins точки разделения, которые могут быть намного меньше.
Для построения гистограмм входные данные X нужно разбить на целочисленные бины. Эта процедура бинирования требует сортировки значений признаков, но она происходит только один раз в самом начале процесса бустинга (не в каждом узле, как в GradientBoostingClassifier и
GradientBoostingRegressor).
Наконец, многие части реализации
HistGradientBoostingClassifier и
HistGradientBoostingRegressor параллелизуются.
Ссылки
Фишер, У.Д. (1958). "On Grouping for Maximum Homogeneity" Journal of the American Statistical Association, 53, 789-798.
1.11.1.2. GradientBoostingClassifier и GradientBoostingRegressor#
Использование и параметры GradientBoostingClassifier и
GradientBoostingRegressor описаны ниже. Два наиболее важных параметра этих оценщиков — n_estimators и learning_rate.
Классификация#
GradientBoostingClassifier поддерживает как бинарную, так и многоклассовую классификацию. Следующий пример показывает, как обучить классификатор градиентного бустинга со 100 решающими пнями в качестве слабых учеников:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913
Количество слабых учеников (т.е. регрессионных деревьев) контролируется параметром n_estimators; Размер каждого дерева можно контролировать либо установкой глубины дерева через max_depth или установкой количества листовых узлов через
max_leaf_nodes. learning_rate является гиперпараметром в диапазоне (0.0, 1.0], который контролирует переобучение через сжатие .
Примечание
Классификация с более чем 2 классами требует индукции n_classes деревьев регрессии на каждой итерации, таким образом, общее количество индуцированных деревьев равно
n_classes * n_estimators. Для наборов данных с большим количеством
классов настоятельно рекомендуется использовать
HistGradientBoostingClassifier в качестве альтернативы
GradientBoostingClassifier .
Регрессия#
GradientBoostingRegressor поддерживает ряд
различных функций потерь
для регрессии, который может быть указан через аргумент
loss; функция потерь по умолчанию для регрессии — квадратичная ошибка
('squared_error').
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(
... n_estimators=100, learning_rate=0.1, max_depth=1, random_state=0,
... loss='squared_error'
... ).fit(X_train, y_train)
>>> mean_squared_error(y_test, est.predict(X_test))
5.00
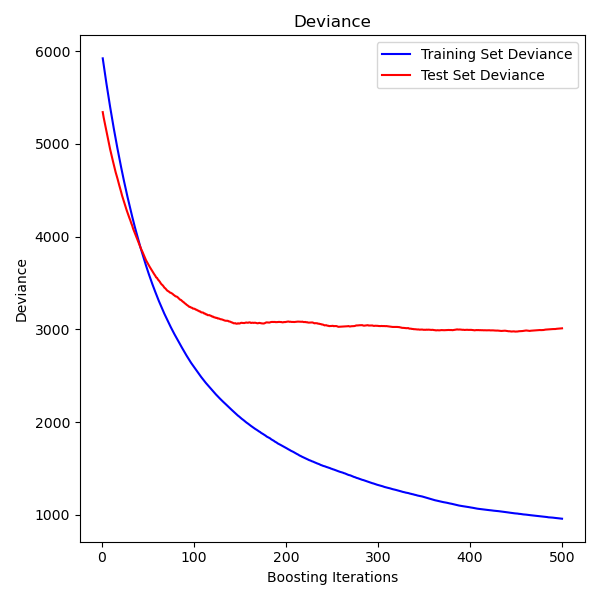
На рисунке ниже показаны результаты применения GradientBoostingRegressor
с наименьшими квадратами потерь и 500 базовыми обучающимися для набора данных по диабету (sklearn.datasets.load_diabetes).
График показывает ошибку обучения и тестирования на каждой итерации.
Ошибка обучения на каждой итерации сохраняется в
train_score_ атрибут модели градиентного бустинга.
Ошибка тестирования на каждой итерации может быть получена
через staged_predict метод, который возвращает генератор, выдающий прогнозы на каждом этапе. Такие графики можно использовать для определения оптимального количества деревьев (т.е. n_estimators) с помощью ранней остановки.
Примеры
1.11.1.2.1. Обучение дополнительных слабых учеников#
Оба GradientBoostingRegressor и GradientBoostingClassifier
поддержка warm_start=True который позволяет добавлять больше оценщиков к уже обученной модели.
>>> import numpy as np
>>> from sklearn.metrics import mean_squared_error
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
>>> X_train, X_test = X[:200], X[200:]
>>> y_train, y_test = y[:200], y[200:]
>>> est = GradientBoostingRegressor(
... n_estimators=100, learning_rate=0.1, max_depth=1, random_state=0,
... loss='squared_error'
... )
>>> est = est.fit(X_train, y_train) # fit with 100 trees
>>> mean_squared_error(y_test, est.predict(X_test))
5.00
>>> _ = est.set_params(n_estimators=200, warm_start=True) # set warm_start and increase num of trees
>>> _ = est.fit(X_train, y_train) # fit additional 100 trees to est
>>> mean_squared_error(y_test, est.predict(X_test))
3.84
1.11.1.2.2. Управление размером дерева#
Размер базовых обучающих регрессионных деревьев определяет уровень взаимодействий переменных, которые могут быть захвачены моделью градиентного бустинга. В целом, дерево глубиной h может захватывать взаимодействия порядка h . Существует два способа контроля размера отдельных деревьев регрессии.
Если вы укажете max_depth=h затем полные бинарные деревья
глубины h будет выращено. Такие деревья будут иметь (максимум) 2**h листовые узлы
и 2**h - 1 разделить узлы.
Альтернативно, вы можете контролировать размер дерева, указав количество листовых узлов через параметр max_leaf_nodes. В этом случае
деревья будут расти с использованием поиска по наилучшему первому шагу, где узлы с наибольшим улучшением
нечистоты будут расширяться первыми.
Дерево с max_leaf_nodes=k имеет k - 1 разделяют узлы и, следовательно, могут
моделировать взаимодействия до порядка max_leaf_nodes - 1 .
Мы обнаружили, что max_leaf_nodes=k дает сопоставимые результаты с max_depth=k-1
но значительно быстрее обучается за счёт немного более высокой ошибки обучения.
Параметр max_leaf_nodes соответствует переменной J в
главе о градиентном бустинге в [Friedman2001] и связан с параметром
interaction.depth в пакете gbm для R, где max_leaf_nodes == interaction.depth + 1 .
1.11.1.2.3. Математическая формулировка#
Сначала мы представляем GBRT для регрессии, а затем детализируем случай классификации.
Регрессия#
GBRT-регрессоры являются аддитивными моделями, чьё предсказание \(\hat{y}_i\) для заданного ввода \(x_i\) имеет следующую форму:
где \(h_m\) являются оценщиками, называемыми слабые обучающиеся в контексте бустинга. Gradient Tree Boosting использует регрессоры дерева решений фиксированного размера в качестве слабых обучаемых. Константа M соответствует
n_estimators параметр.
Как и другие алгоритмы бустинга, GBRT строится жадным образом:
где недавно добавленное дерево \(h_m\) на экземпляре оценщика, облегчая декодирование через методы прогнозирования и преобразования. \(L_m\), учитывая предыдущий ансамбль \(F_{m-1}\):
где \(l(y_i, F(x_i))\) определяется loss параметр, подробно описанный в следующем разделе.
По умолчанию, начальная модель \(F_{0}\) выбирается как константа, минимизирующая потери: для потерь по методу наименьших квадратов это эмпирическое среднее целевых значений. Начальная модель также может быть указана через init
аргумент.
Используя аппроксимацию Тейлора первого порядка, значение \(l\) может быть приближён следующим образом:
Примечание
Кратко, аппроксимация Тейлора первого порядка утверждает, что \(l(z) \approx l(a) + (z - a) \frac{\partial l}{\partial z}(a)\). Здесь, \(z\) соответствует \(F_{m - 1}(x_i) + h_m(x_i)\), и \(a\) соответствует \(F_{m-1}(x_i)\)
Количество \(\left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]_{F=F_{m - 1}}\) является производной функции потерь по ее второму параметру, вычисленной в \(F_{m-1}(x)\). Это легко вычислить для любого заданного \(F_{m - 1}(x_i)\) в замкнутой форме, поскольку функция потерь дифференцируема. Мы обозначим ее как \(g_i\).
Удаляя постоянные члены, получаем:
Это минимизируется, если \(h(x_i)\) обучен предсказывать значение, пропорциональное отрицательному градиенту \(-g_i\). Поэтому на каждой итерации оценщик \(h_m\) обучен для предсказания отрицательных градиентов образцов. Градиенты обновляются на каждой итерации. Это можно рассматривать как своего рода градиентный спуск в функциональном пространстве.
Примечание
Для некоторых функций потерь, например, 'absolute_error' где градиенты \(\pm 1\), значения, предсказанные обученным \(h_m\) недостаточно
точны: дерево может выводить только целочисленные значения. В результате
значения листьев дерева \(h_m\) изменяются после подгонки дерева,
так что значения листьев минимизируют потери \(L_m\)Обновление зависит от функции потерь: для функции потерь абсолютной ошибки значение листа обновляется до медианы выборок в этом листе.
Классификация#
Градиентный бустинг для классификации очень похож на случай регрессии. Однако сумма деревьев \(F_M(x_i) = \sum_m h_m(x_i)\) не однороден предсказанию: он не может быть классом, поскольку деревья предсказывают непрерывные значения.
Отображение от значения \(F_M(x_i)\) к классу или вероятности зависит от функции потерь. Для логарифмических потерь вероятность того, что \(x_i\) принадлежит положительному классу, моделируется как \(p(y_i = 1 | x_i) = \sigma(F_M(x_i))\) где \(\sigma\) является сигмоидной или экспоненциальной функцией.
Для многоклассовой классификации K деревьев (для K классов) строятся на каждом из \(M\) итерации. Вероятность того, что \(x_i\) принадлежит классу k моделируется как softmax от \(F_{M,k}(x_i)\) значения.
Обратите внимание, что даже для задачи классификации \(h_m\) суб-оценщик всё ещё является регрессором, а не классификатором. Это потому, что суб-оценщики обучаются предсказывать (отрицательные) градиенты, которые всегда являются непрерывными величинами.
1.11.1.2.4. Функции потерь#
Следующие функции потерь поддерживаются и могут быть указаны с помощью параметра loss:
Регрессия#
Квадратичная ошибка (
'squared_error'): Естественный выбор для регрессии из-за его превосходных вычислительных свойств. Начальная модель задается средним значением целевых переменных.Абсолютная ошибка (
'absolute_error'): Надежная функция потерь для регрессии. Исходная модель задается медианой целевых значений.Хьюбер (
'huber'): Еще одна устойчивая функция потерь, которая объединяет метод наименьших квадратов и метод наименьших абсолютных отклонений; используйтеalphaдля управления чувствительностью к выбросам (см. [Friedman2001] для более подробной информации).Квантиль (
'quantile'): Функция потерь для квантильной регрессии. Используйте0 < alpha < 1чтобы указать квантиль. Эта функция потерь может использоваться для создания интервалов предсказания (см. Интервалы прогнозирования для регрессии градиентного бустинга).
Классификация#
Бинарная логарифмическая потеря (
'log-loss'): Биномиальная функция потерь с отрицательным логарифмическим правдоподобием для бинарной классификации. Она предоставляет вероятностные оценки. Исходная модель задается логарифмом отношения шансов.Многоклассовая логарифмическая потеря (
'log-loss'): Функция потерь мультиномиального отрицательного логарифма правдоподобия для многоклассовой классификации сn_classesвзаимоисключающие классы. Он предоставляет вероятностные оценки. Исходная модель задается априорной вероятностью каждого класса. На каждой итерацииn_classesдолжны быть построены деревья регрессии, что делает GBRT довольно неэффективным для наборов данных с большим количеством классов.Экспоненциальная потеря (
'exponential'): Та же функция потерь, что иAdaBoostClassifier. Менее устойчив к неправильно помеченным примерам, чем'log-loss'; может использоваться только для бинарной классификации.
1.11.1.2.5. Сжатие через скорость обучения#
[Friedman2001] предложил простую стратегию регуляризации, которая масштабирует вклад каждого слабого обучающегося на постоянный коэффициент \(\nu\):
Параметр \(\nu\) также называется скорость обучения потому что
он масштабирует длину шага процедуры градиентного спуска; он может
быть установлен через learning_rate параметр.
Параметр learning_rate сильно взаимодействует с параметром
n_estimators, количество слабых обучающихся для подгонки. Меньшие значения learning_rate требуют большего количества слабых обучаемых для поддержания постоянной ошибки обучения. Эмпирические данные показывают, что малые значения learning_rate предпочитают лучшую ошибку тестирования. [HTF]
рекомендуется установить скорость обучения на небольшую константу (например, learning_rate <= 0.1) и выбрать n_estimators достаточно большим, чтобы применялось раннее остановление, см. Ранняя остановка в градиентном бустинге
для более подробного обсуждения взаимодействия между
learning_rate и n_estimators см. [R2007].
1.11.1.2.6. Субдискретизация#
[Friedman2002] предложил стохастическое градиентное бустирование, которое сочетает градиентный
бустинг с усреднением по бутстрапу (бэггинг). На каждой итерации
базовый классификатор обучается на доле subsample доступных обучающих данных. Подвыборка извлекается без возвращения. Типичное значение subsample равно 0.5.
На рисунке ниже показано влияние сжатия и субдискретизации на качество соответствия модели. Мы можем чётко видеть, что сжатие превосходит отсутствие сжатия. Субдискретизация со сжатием может дополнительно повысить точность модели. Субдискретизация без сжатия, с другой стороны, работает плохо.
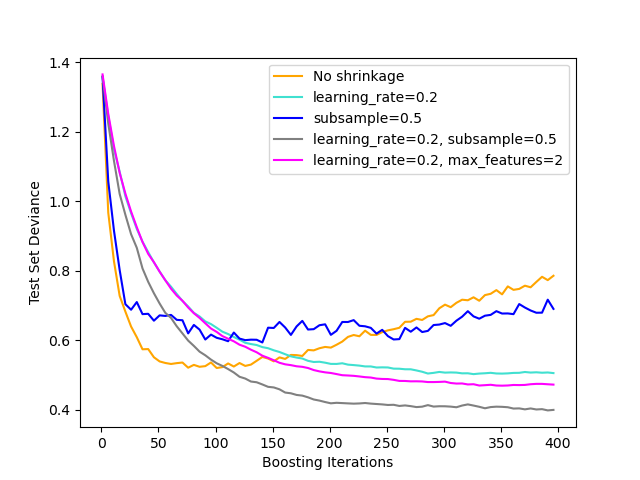
Другая стратегия для уменьшения дисперсии — это субдискретизация признаков
аналогично случайным разбиениям в RandomForestClassifier. Количество субдискретизированных признаков можно контролировать через max_features
параметр.
Примечание
Использование небольшого max_features значение может значительно уменьшить время выполнения.
Стохастическое градиентное бустирование позволяет вычислять out-of-bag оценки тестового отклонения, вычисляя улучшение отклонения на примерах, которые не включены в бутстрап-выборку (т.е. out-of-bag примеры). Улучшения сохраняются в атрибуте oob_improvement_.
oob_improvement_[i] содержит улучшение в терминах потерь на OOB-выборках, если добавить i-й этап к текущим прогнозам. Оценки out-of-bag могут использоваться для выбора модели, например, для определения оптимального количества итераций. OOB-оценки обычно очень пессимистичны, поэтому мы рекомендуем использовать кросс-валидацию и применять OOB только если кросс-валидация занимает слишком много времени.
Примеры
1.11.1.2.7. Интерпретация с важностью признаков#
Отдельные деревья решений можно легко интерпретировать, просто визуализируя структуру дерева. Однако модели градиентного бустинга состоят из сотен регрессионных деревьев, поэтому их нельзя легко интерпретировать визуальным осмотром отдельных деревьев. К счастью, было предложено несколько методов для обобщения и интерпретации моделей градиентного бустинга.
Часто признаки вносят неодинаковый вклад в предсказание целевой переменной; во многих ситуациях большинство признаков фактически нерелевантны. При интерпретации модели первый вопрос обычно таков: какие признаки важны и как они способствуют предсказанию целевой переменной?
Отдельные деревья решений внутренне выполняют отбор признаков, выбирая подходящие точки разделения. Эта информация может быть использована для измерения важности каждого признака; основная идея: чем чаще признак используется в точках разделения дерева, тем важнее этот признак. Это понятие важности может быть расширено на ансамбли деревьев решений путем простого усреднения важности признаков на основе нечистоты каждого дерева (см. Оценка важности признаков для получения дополнительных деталей).
Оценки важности признаков обученной модели градиентного бустинга могут быть
получены через feature_importances_ свойство:
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([0.107, 0.105, 0.113, 0.0987, 0.0947,
0.107, 0.0916, 0.0972, 0.0958, 0.0906])
Обратите внимание, что это вычисление важности признаков основано на энтропии и отличается от sklearn.inspection.permutation_importance который
основан на перестановке признаков.
Примеры
Ссылки
Friedman, J.H. (2001). Жадная аппроксимация функций: градиентный бустинг-машина. Annals of Statistics, 29, 1189-1232.
Фридман, Дж.Х. (2002). Стохастическое градиентное бустирование.. Computational Statistics & Data Analysis, 38, 367-378.
G. Ridgeway (2006). Generalized Boosted Models: A guide to the gbm package
1.11.2. Случайные леса и другие ансамбли рандомизированных деревьев#
The sklearn.ensemble модуль включает два алгоритма усреднения, основанных
на рандомизированных деревья решений: алгоритм RandomForest и метод Extra-Trees. Оба алгоритма являются техниками perturb-and-combine [B1998] специально разработан для деревьев. Это означает, что создается разнообразный набор классификаторов путем внесения случайности в построение классификатора. Прогноз ансамбля выдается как усредненный прогноз отдельных классификаторов.
Как и другие классификаторы, классификаторы леса должны быть обучены с двумя массивами: разреженным или плотным массивом X формы (n_samples, n_features)
содержащий обучающие выборки, и массив Y формы (n_samples,)
содержащий целевые значения (метки классов) для обучающих выборок:
>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, Y)
Как деревья решений, леса деревьев также расширяются до
многомерные задачи (если Y - массив
формы (n_samples, n_outputs)).
1.11.2.1. Случайные леса#
В случайных лесах (см. RandomForestClassifier и
RandomForestRegressor классы), каждое дерево в ансамбле строится из выборки, взятой с возвращением (т.е. бутстрап-выборки) из обучающего набора.
При построении каждого дерева в лесу рассматривается случайное подмножество признаков. Размер этого подмножества контролируется параметром
max_features параметр; он может включать либо все входные признаки, либо случайное
подмножество из них (см. рекомендации по настройке параметров для получения дополнительных деталей).
Цель этих двух источников случайности (бутстрэппинг выборок и случайный выбор признаков на каждом разбиении) — уменьшить дисперсию оценки леса. Действительно, отдельные деревья решений обычно демонстрируют высокую дисперсию и склонны к переобучению. Внесённая случайность в лесах приводит к деревьям решений с несколько разобщёнными ошибками предсказания. Усредняя эти предсказания, некоторые ошибки могут компенсироваться. Случайные леса достигают снижения дисперсии за счёт комбинирования разнообразных деревьев, иногда ценой небольшого увеличения смещения. На практике снижение дисперсии часто значимо, что даёт в целом лучшую модель.
При выращивании каждого дерева в лесу, "лучшее" разделение (т.е. эквивалентно
передаче splitter="best" к базовым деревьям решений) выбирается в соответствии
с критерием нечистоты. См. Математическая формулировка CART для получения дополнительной информации.
В отличие от оригинальной публикации [B2001], реализация scikit-learn объединяет классификаторы путём усреднения их вероятностных предсказаний, вместо того чтобы позволить каждому классификатору голосовать за один класс.
Конкурентной альтернативой случайным лесам являются Градиентный бустинг на основе гистограмм (HGBT) моделей:
Построение деревьев: Случайные леса обычно полагаются на глубокие деревья (которые переобучаются индивидуально), использующие много вычислительных ресурсов, так как требуют нескольких разбиений и оценок кандидатных разбиений. Бустинговые модели строят неглубокие деревья (которые недообучаются индивидуально), которые быстрее обучать и предсказывать.
Последовательный бустинг: В HGBT деревья решений строятся последовательно, где каждое дерево обучается для исправления ошибок, допущенных предыдущими. Это позволяет им итеративно улучшать производительность модели, используя относительно мало деревьев. В отличие от этого, случайные леса используют большинство голосов для прогнозирования результата, что может потребовать большего количества деревьев для достижения того же уровня точности.
Эффективное бинирование: HGBT использует эффективный алгоритм бинирования, который может обрабатывать большие наборы данных с большим количеством признаков. Алгоритм бинирования может предварительно обрабатывать данные для ускорения последующего построения дерева (см. Почему это быстрее). В отличие от этого, реализация случайных лесов в scikit-learn не использует бининг и полагается на точное разделение, что может быть вычислительно затратным.
В целом, вычислительная стоимость HGBT по сравнению с RF зависит от конкретных характеристик набора данных и задачи моделирования. Рекомендуется попробовать обе модели и сравнить их производительность и вычислительную эффективность на вашей конкретной задаче, чтобы определить, какая модель лучше подходит.
Примеры
1.11.2.2. Чрезвычайно рандомизированные деревья#
В экстремально рандомизированных деревьях (см. ExtraTreesClassifier
и ExtraTreesRegressor классов), случайность идет на шаг дальше в способе вычисления разбиений. Как и в случайных лесах, используется случайное подмножество кандидатных признаков, но вместо поиска наиболее дискриминативных порогов, пороги выбираются случайно для каждого кандидатного признака, и лучший из этих случайно сгенерированных порогов выбирается в качестве правила разбиения. Это обычно позволяет немного уменьшить дисперсию модели, за счет немного большего увеличения смещения:
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import make_blobs
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_blobs(n_samples=10000, n_features=10, centers=100,
... random_state=0)
>>> clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,
... random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.98)
>>> clf = RandomForestClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.999)
>>> clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,
... min_samples_split=2, random_state=0)
>>> scores = cross_val_score(clf, X, y, cv=5)
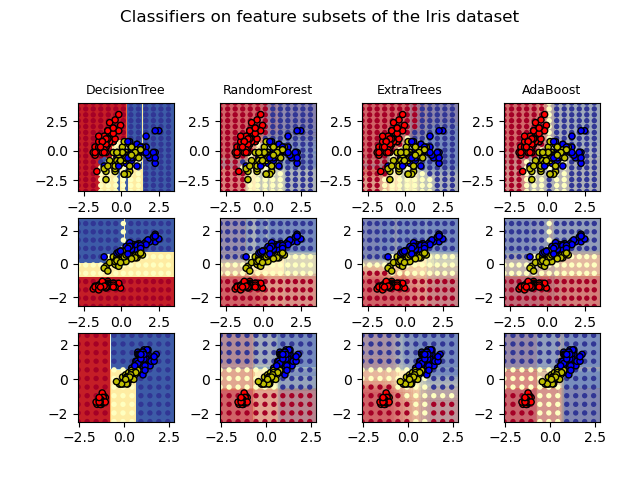
>>> scores.mean() > 0.999
np.True_
1.11.2.3. Параметры#
Основные параметры для настройки при использовании этих методов — это n_estimators и
max_featuresданные без скрытого повышения типа. Тип данных сохраняется
max_features=1.0 или эквивалентно max_features=None (всегда рассматривая
все признаки вместо случайного подмножества) для задач регрессии, и
max_features="sqrt" (используя случайное подмножество размера sqrt(n_features))
для задач классификации (где n_features — это количество признаков в
данных). Значение по умолчанию max_features=1.0 эквивалентно бэггированным
деревьям, и большая случайность может быть достигнута установкой меньших значений (например, 0.3
является типичным значением по умолчанию в литературе). Хорошие результаты часто достигаются при
установке max_depth=None в комбинации с min_samples_split=2 (т.е., при полном развитии деревьев). Однако имейте в виду, что эти значения обычно не являются оптимальными и могут привести к моделям, потребляющим много оперативной памяти. Лучшие значения параметров всегда должны быть проверены с помощью кросс-валидации. Кроме того, обратите внимание, что в случайных лесах по умолчанию используются бутстрап-выборки (bootstrap=True), в то время как стратегия по умолчанию для extra-trees — использовать
весь набор данных (bootstrap=False). При использовании бутстрап-выборки ошибка обобщения может быть оценена на исключённых или out-of-bag выборках. Это можно включить, установив oob_score=True.
Примечание
Размер модели с параметрами по умолчанию составляет \(O( M * N * log (N) )\),
где \(M\) это количество деревьев и \(N\) это количество образцов. Чтобы уменьшить размер модели, вы можете изменить эти параметры:
min_samples_split, max_leaf_nodes, max_depth и min_samples_leaf.
1.11.2.4. Параллелизация#
Наконец, этот модуль также включает параллельное построение деревьев и параллельное вычисление предсказаний через n_jobs
параметр. Если n_jobs=k затем вычисления разделяются на
k jobs, и запускаются на k ядер машины. Если n_jobs=-1
то используются все доступные ядра на машине. Обратите внимание, что из-за
накладных расходов на межпроцессное взаимодействие ускорение может быть нелинейным
(т.е. использование k задачи, к сожалению, не будут k раз
быстрее). Значительное ускорение все же может быть достигнуто при построении
большого количества деревьев или когда построение одного дерева требует значительного
времени (например, на больших наборах данных).
Примеры
Ссылки
Брейман, «Случайные леса», Machine Learning, 45(1), 5-32, 2001.
Брейман, «Arcing Classifiers», Annals of Statistics 1998.
P. Geurts, D. Ernst. и L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
1.11.2.5. Оценка важности признаков#
Относительный ранг (т.е. глубина) признака, используемого как узел решения в дереве, может использоваться для оценки относительной важности этого признака относительно предсказуемости целевой переменной. Признаки, используемые в верхней части дерева, вносят вклад в окончательное решение предсказания большей доли входных выборок. ожидаемая доля выборок в которые они вносят вклад, таким образом могут использоваться как оценка относительная важность признаков. В scikit-learn доля образцов, которую вносит признак, комбинируется с уменьшением нечистоты от их разделения для создания нормализованной оценки предсказательной силы этого признака.
По усреднение оценки предсказательной способности по нескольким рандомизированным деревьям можно уменьшить дисперсию такой оценки и использовать её для отбора признаков. Это известно как среднее уменьшение неоднородности (MDI). См. [L2014] для получения дополнительной информации о MDI и оценке важности признаков с помощью Random Forests.
Предупреждение
Важности признаков на основе нечистоты, вычисленные на древовидных моделях, страдают от двух недостатков, которые могут привести к вводящим в заблуждение выводам. Во-первых, они вычисляются на статистиках, полученных из обучающего набора данных, и поэтому не обязательно информируют нас о том, какие признаки наиболее важны для получения хороших прогнозов на отложенном наборе данных. Во-вторых, они отдают предпочтение признакам с высокой кардинальностью, то есть признаки со многими уникальными значениями. Важность признаков на основе перестановок является альтернативой важности признаков на основе нечистоты, которая не страдает от этих недостатков. Эти два метода получения важности признаков исследуются в: Важность перестановок против важности признаков случайного леса (MDI).
На практике эти оценки хранятся как атрибут с именем
feature_importances_ на обученной модели. Это массив формы
(n_features,) значения которых положительны и суммируются до 1.0. Чем выше значение, тем важнее вклад соответствующего признака в функцию прогнозирования.
Примеры
Ссылки
G. Louppe, “Understanding Random Forests: From Theory to Practice”, докторская диссертация, Университет Льежа, 2014.
1.11.2.6. Полностью случайные деревья вложения#
RandomTreesEmbedding реализует неконтролируемое преобразование данных. Используя лес полностью случайных деревьев, RandomTreesEmbedding
кодирует данные индексами листьев, в которые попадает точка данных. Этот
индекс затем кодируется методом one-of-K, что приводит к высокоразмерному,
разреженному бинарному кодированию.
Это кодирование может быть вычислено очень эффективно и затем использовано как основа
для других задач обучения.
Размер и разреженность кода могут быть изменены выбором количества
деревьев и максимальной глубины для каждого дерева. Для каждого дерева в ансамбле кодирование
содержит одну единицу. Размер кодирования не превышает n_estimators * 2
** max_depth, максимальное количество листьев в лесу.
Поскольку соседние точки данных с большей вероятностью находятся в одном листе дерева, преобразование выполняет неявную, непараметрическую оценку плотности.
Примеры
Преобразование признаков с хешированием с использованием полностью случайных деревьев
Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap… сравнивает нелинейные методы снижения размерности на рукописных цифрах.
Преобразования признаков с ансамблями деревьев сравнивает контролируемые и неконтролируемые преобразования признаков на основе деревьев.
Смотрите также
Обучение многообразию методы также могут быть полезны для получения нелинейных представлений пространства признаков, также эти подходы фокусируются на снижении размерности.
1.11.2.7. Добавление дополнительных деревьев#
RandomForest, Extra-Trees и RandomTreesEmbedding оценщики все поддерживают
warm_start=True что позволяет добавлять больше деревьев к уже обученной модели.
>>> from sklearn.datasets import make_classification
>>> from sklearn.ensemble import RandomForestClassifier
>>> X, y = make_classification(n_samples=100, random_state=1)
>>> clf = RandomForestClassifier(n_estimators=10)
>>> clf = clf.fit(X, y) # fit with 10 trees
>>> len(clf.estimators_)
10
>>> # set warm_start and increase num of estimators
>>> _ = clf.set_params(n_estimators=20, warm_start=True)
>>> _ = clf.fit(X, y) # fit additional 10 trees
>>> len(clf.estimators_)
20
Когда random_state также установлен, внутреннее случайное состояние также сохраняется между fit вызовов. Это означает, что обучение модели один раз с n оценщиков совпадает с построением модели итеративно через несколько fit вызовов, где окончательное количество оценщиков равно n.
>>> clf = RandomForestClassifier(n_estimators=20) # set `n_estimators` to 10 + 10
>>> _ = clf.fit(X, y) # fit `estimators_` will be the same as `clf` above
Обратите внимание, что это отличается от обычного поведения random_state в том, что он не не приводит к одинаковому результату при разных вызовах.
1.11.3. Мета-оценщик бэггинга#
В ансамблевых алгоритмах методы бэггинга образуют класс алгоритмов, которые строят несколько экземпляров черного ящика-оценивателя на случайных подмножествах исходного обучающего набора, а затем агрегируют их индивидуальные предсказания для формирования окончательного предсказания. Эти методы используются как способ уменьшения дисперсии базового оценивателя (например, дерева решений), путем введения рандомизации в его процедуру построения и затем создания ансамбля из него. Во многих случаях методы бэггинга представляют собой очень простой способ улучшения по сравнению с единственной моделью, без необходимости адаптации базового алгоритма. Поскольку они предоставляют способ уменьшить переобучение, методы бэггинга работают лучше всего с сильными и сложными моделями (например, полностью развитыми деревьями решений), в отличие от методов бустинга, которые обычно работают лучше всего со слабыми моделями (например, неглубокими деревьями решений).
Методы бэггинга бывают разных видов, но в основном отличаются друг от друга способом, которым они выбирают случайные подмножества обучающего набора:
Когда случайные подмножества набора данных выбираются как случайные подмножества выборок, этот алгоритм известен как Pasting [B1999].
Когда образцы извлекаются с возвращением, метод известен как Bagging [B1996].
Когда случайные подмножества набора данных выбираются как случайные подмножества признаков, метод известен как Random Subspaces [H1998].
Наконец, когда базовые оценки строятся на подмножествах как выборок, так и признаков, метод известен как Random Patches. [LG2012].
В scikit-learn методы бэггинга предлагаются как унифицированный
BaggingClassifier мета-оценщик (соответственно BaggingRegressor),
принимая в качестве входных данных пользовательский оценщик вместе с параметрами,
определяющими стратегию выборки случайных подмножеств. В частности, max_samples
и max_features контролировать размер подмножеств (в терминах образцов и признаков), в то время как bootstrap и bootstrap_features управляют тем, выбираются ли образцы и признаки с заменой или без замены. При использовании подмножества доступных образцов точность обобщения может быть оценена с помощью образцов вне выборки, установив oob_score=True. В качестве примера, фрагмент ниже иллюстрирует, как создать ансамбль бэггинга из
KNeighborsClassifier оценщики, каждый построен на случайных
подмножествах 50% выборок и 50% признаков.
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
... max_samples=0.5, max_features=0.5)
Примеры
Ссылки
L. Breiman, “Pasting small votes for classification in large databases and on-line”, Machine Learning, 36(1), 85-103, 1999.
L. Breiman, "Bagging predictors", Machine Learning, 24(2), 123-140, 1996.
T. Ho, "The random subspace method for constructing decision forests", Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.
G. Louppe и P. Geurts, «Ensembles on Random Patches», Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.
1.11.4. Голосующий классификатор#
Идея, лежащая в основе VotingClassifier заключается в объединении
концептуально различных классификаторов машинного обучения и использовании мажоритарного голосования
или усреднённых предсказанных вероятностей (мягкое голосование) для предсказания меток классов.
Такой классификатор может быть полезен для набора одинаково хорошо работающих моделей
с целью компенсации их индивидуальных слабостей.
1.11.4.1. Метки большинства классов (Мажоритарное/Жёсткое голосование)#
При мажоритарном голосовании предсказанный метка класса для конкретного образца — это метка класса, представляющая большинство (моду) меток классов, предсказанных каждым отдельным классификатором.
Например, если прогноз для данного образца
классификатор 1 -> класс 1
классификатор 2 -> класс 1
классификатор 3 -> класс 2
VotingClassifier (с voting='hard') классифицировал бы образец как "класс 1" на основе метки большинства классов.
В случае ничьей, VotingClassifier выберет класс на основе порядка сортировки по возрастанию. Например, в следующем сценарии
классификатор 1 -> класс 2
классификатор 2 -> класс 1
метка класса 1 будет присвоена образцу.
1.11.4.2. Использование#
Следующий пример показывает, как обучить классификатор по правилу большинства:
>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier
>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='hard')
>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
... scores = cross_val_score(clf, X, y, scoring='accuracy', cv=5)
... print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.95 (+/- 0.04) [Logistic Regression]
Accuracy: 0.94 (+/- 0.04) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.04) [Ensemble]
1.11.4.3. Взвешенные средние вероятности (Мягкое голосование)#
В отличие от голосования большинством (жесткое голосование), мягкое голосование возвращает метку класса как argmax суммы предсказанных вероятностей.
Конкретные веса могут быть назначены каждому классификатору через weights
параметр. При указании весов предсказанные вероятности классов для каждого классификатора собираются, умножаются на вес классификатора и усредняются. Итоговая метка класса затем выводится из метки класса с наибольшей средней вероятностью.
Чтобы проиллюстрировать это на простом примере, предположим, что у нас есть 3 классификатора и задача классификации на 3 класса, где мы назначаем равные веса всем классификаторам: w1=1, w2=1, w3=1.
Взвешенные средние вероятности для образца затем рассчитываются следующим образом:
классификатор |
класс 1 |
класс 2 |
класс 3 |
|---|---|---|---|
классификатор 1 |
w1 * 0.2 |
w1 * 0.5 |
w1 * 0.3 |
классификатор 2 |
w2 * 0.6 |
w2 * 0.3 |
w2 * 0.1 |
классификатор 3 |
w3 * 0.3 |
w3 * 0.4 |
w3 * 0.3 |
взвешенное среднее |
0.37 |
0.4 |
0.23 |
Здесь предсказанная метка класса — 2, поскольку она имеет наивысшую среднюю предсказанную вероятность. См. пример на Визуализация вероятностных предсказаний VotingClassifier для демонстрации того, как предсказанная метка класса может быть получена из взвешенного среднего предсказанных вероятностей.
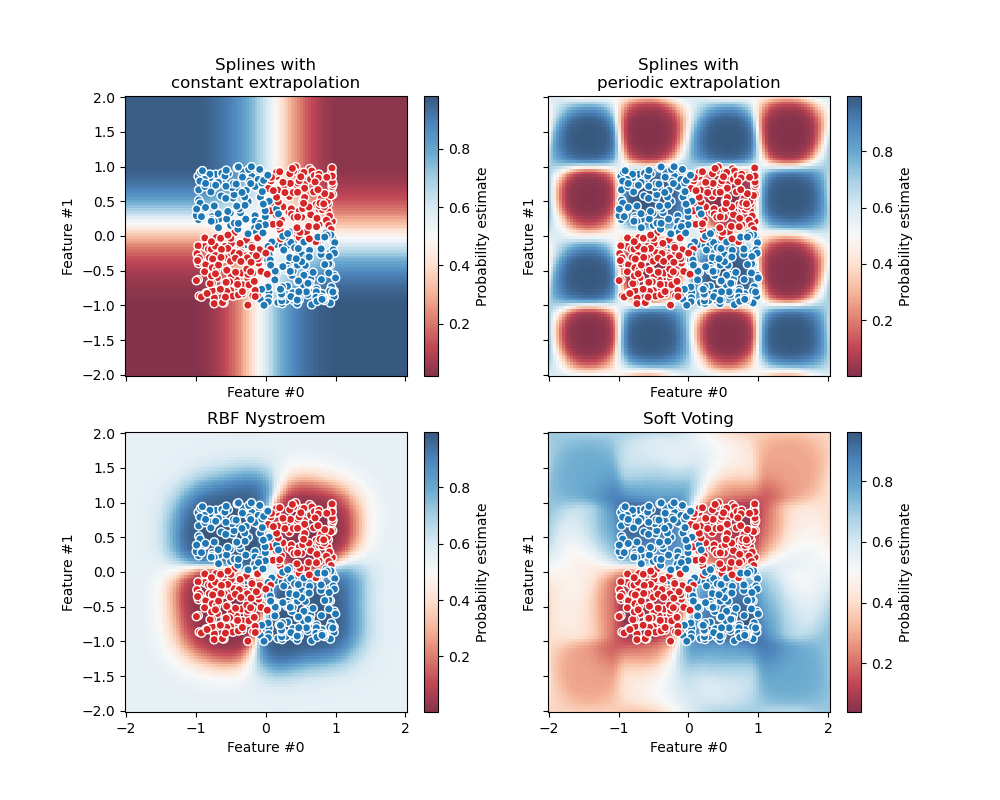
Следующий рисунок иллюстрирует, как могут измениться области решений при
мягком VotingClassifier обучается с весами на трёх линейных моделях:
1.11.4.4. Использование#
Чтобы предсказать метки классов на основе предсказанных
вероятностей классов (оценщики scikit-learn в VotingClassifier
должны поддерживать predict_proba метод):
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft'
... )
Опционально могут быть предоставлены веса для отдельных классификаторов:
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft', weights=[2,5,1]
... )
Используя VotingClassifier с GridSearchCV#
The VotingClassifier также может использоваться вместе с
GridSearchCV для настройки
гиперпараметров отдельных оценщиков:
>>> from sklearn.model_selection import GridSearchCV
>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()
>>> eclf = VotingClassifier(
... estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft'
... )
>>> params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200]}
>>> grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
>>> grid = grid.fit(iris.data, iris.target)
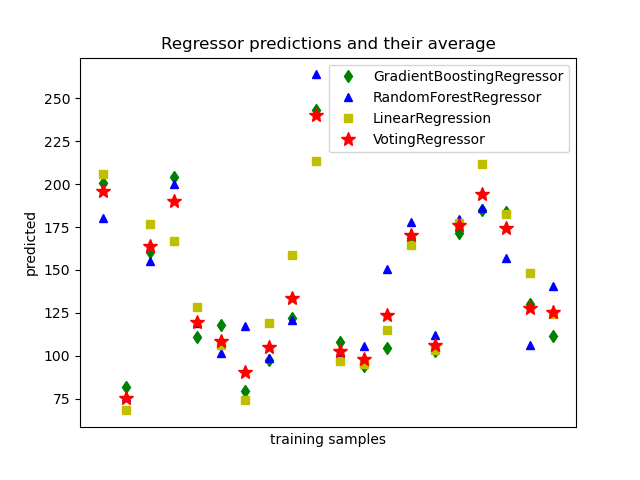
1.11.5. Voting Regressor#
Идея, лежащая в основе VotingRegressor состоит в объединении концептуально
различных регрессоров машинного обучения и возврате средних предсказанных значений.
Такой регрессор может быть полезен для набора одинаково хорошо работающих моделей,
чтобы сбалансировать их индивидуальные слабости.
1.11.5.1. Использование#
Следующий пример показывает, как обучить VotingRegressor:
>>> from sklearn.datasets import load_diabetes
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import VotingRegressor
>>> # Loading some example data
>>> X, y = load_diabetes(return_X_y=True)
>>> # Training classifiers
>>> reg1 = GradientBoostingRegressor(random_state=1)
>>> reg2 = RandomForestRegressor(random_state=1)
>>> reg3 = LinearRegression()
>>> ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
>>> ereg = ereg.fit(X, y)
Примеры
1.11.6. Стекинг (Stacked generalization)#
Стекинг (обобщение) — это метод объединения оценщиков для уменьшения их смещений [W1992] [HTF]. Точнее, предсказания каждого отдельного оценщика объединяются и используются как вход для финального оценщика для вычисления предсказания. Этот финальный оценщик обучается через перекрёстную проверку.
The StackingClassifier и StackingRegressor предоставляют такие стратегии, которые могут применяться к задачам классификации и регрессии.
The estimators параметр соответствует списку оценщиков, которые объединены параллельно на входных данных. Он должен быть задан как список имен и оценщиков:
>>> from sklearn.linear_model import RidgeCV, LassoCV
>>> from sklearn.neighbors import KNeighborsRegressor
>>> estimators = [('ridge', RidgeCV()),
... ('lasso', LassoCV(random_state=42)),
... ('knr', KNeighborsRegressor(n_neighbors=20,
... metric='euclidean'))]
The final_estimator будет использовать предсказания estimators в качестве входных данных. Он
должен быть классификатором или регрессором при использовании StackingClassifier
или StackingRegressor, соответственно:
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.ensemble import StackingRegressor
>>> final_estimator = GradientBoostingRegressor(
... n_estimators=25, subsample=0.5, min_samples_leaf=25, max_features=1,
... random_state=42)
>>> reg = StackingRegressor(
... estimators=estimators,
... final_estimator=final_estimator)
Для обучения estimators и final_estimator, fit метод должен быть вызван на обучающих данных:
>>> from sklearn.datasets import load_diabetes
>>> X, y = load_diabetes(return_X_y=True)
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... random_state=42)
>>> reg.fit(X_train, y_train)
StackingRegressor(...)
Во время обучения estimators обучаются на всех обучающих данных
X_train. Они будут использоваться при вызове predict или predict_proba. Для обобщения и избежания переобучения, final_estimator обучается на внешних выборках с использованием sklearn.model_selection.cross_val_predict внутренне.
Для StackingClassifier, обратите внимание, что выход estimators управляется параметром stack_method и вызывается каждым оценщиком.
Этот параметр является либо строкой, содержащей имена методов оценщика, либо 'auto'
, который автоматически определит доступный метод в зависимости от доступности, проверяя в порядке предпочтения: predict_proba,
decision_function и predict.
A StackingRegressor и StackingClassifier может использоваться как
любой другой регрессор или классификатор, предоставляя predict, predict_proba, или
decision_function метод, например:
>>> y_pred = reg.predict(X_test)
>>> from sklearn.metrics import r2_score
>>> print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))
R2 score: 0.53
Обратите внимание, что также можно получить выходные данные стекированной
estimators используя transform method:
>>> reg.transform(X_test[:5])
array([[142, 138, 146],
[179, 182, 151],
[139, 132, 158],
[286, 292, 225],
[126, 124, 164]])
На практике стекинг-предсказатель предсказывает так же хорошо, как лучший предсказатель базового слоя, а иногда даже превосходит его, комбинируя различные сильные стороны этих предсказателей. Однако обучение стекинг-предсказателя вычислительно затратно.
Примечание
Для StackingClassifier, при использовании stack_method_='predict_proba', первый столбец отбрасывается, когда задача является задачей бинарной классификации. Действительно, оба столбца вероятностей, предсказанных каждым оценщиком, идеально коллинеарны.
Примечание
Несколько слоев стекинга могут быть достигнуты путем назначения final_estimator в StackingClassifier или StackingRegressor:
>>> final_layer_rfr = RandomForestRegressor(
... n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer_gbr = GradientBoostingRegressor(
... n_estimators=10, max_features=1, max_leaf_nodes=5,random_state=42)
>>> final_layer = StackingRegressor(
... estimators=[('rf', final_layer_rfr),
... ('gbrt', final_layer_gbr)],
... final_estimator=RidgeCV()
... )
>>> multi_layer_regressor = StackingRegressor(
... estimators=[('ridge', RidgeCV()),
... ('lasso', LassoCV(random_state=42)),
... ('knr', KNeighborsRegressor(n_neighbors=20,
... metric='euclidean'))],
... final_estimator=final_layer
... )
>>> multi_layer_regressor.fit(X_train, y_train)
StackingRegressor(...)
>>> print('R2 score: {:.2f}'
... .format(multi_layer_regressor.score(X_test, y_test)))
R2 score: 0.53
Примеры
Ссылки
Волперт, Дэвид Х. «Сложенное обобщение». Neural networks 5.2 (1992): 241-259.
1.11.7. AdaBoost#
Модуль sklearn.ensemble включает популярный алгоритм бустинга
AdaBoost, представленный в 1995 году Фройндом и Шапире [FS1995].
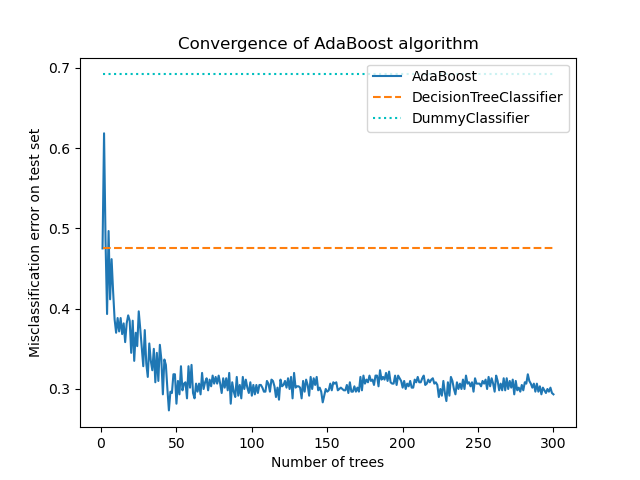
Основной принцип AdaBoost заключается в обучении последовательности слабых учеников (т.е. моделей, которые лишь немного лучше случайного угадывания, таких как небольшие деревья решений) на многократно модифицированных версиях данных. Прогнозы от всех них затем объединяются через взвешенное большинство голосов (или сумму) для получения окончательного прогноза. Модификации данных на каждой так называемой итерации бустинга состоят в применении весов \(w_1\), \(w_2\), …, \(w_N\) для каждого из обучающих образцов. Изначально все эти веса установлены в \(w_i = 1/N\), так что первый шаг просто обучает слабый классификатор на исходных данных. Для каждой последующей итерации веса выборок индивидуально изменяются, и алгоритм обучения применяется повторно к перевзвешенным данным. На данном шаге те обучающие примеры, которые были неправильно предсказаны бустинговой моделью, индуцированной на предыдущем шаге, получают увеличенные веса, в то время как веса уменьшаются для тех, которые были предсказаны правильно. По мере продвижения итераций примеры, которые трудно предсказать, получают все большее влияние. Каждый последующий слабый классификатор тем самым вынужден концентрироваться на примерах, которые были пропущены предыдущими в последовательности [HTF].
AdaBoost можно использовать как для задач классификации, так и для регрессии:
Для многоклассовой классификации,
AdaBoostClassifierреализует AdaBoost.SAMME [ZZRH2009].Для регрессии,
AdaBoostRegressorреализует AdaBoost.R2 [D1997].
1.11.7.1. Использование#
Следующий пример показывает, как обучить классификатор AdaBoost со 100 слабыми обучающимися:
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> X, y = load_iris(return_X_y=True)
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores.mean()
np.float64(0.95)
Количество слабых обучаемых контролируется параметром n_estimators.
learning_rate параметр управляет вкладом слабых обучающихся в
финальную комбинацию. По умолчанию слабые обучающиеся — это решающие пни. Различные
слабые обучающиеся могут быть указаны через estimator параметр.
Основные параметры для настройки для получения хороших результатов — это n_estimators и сложность базовых оценщиков (например, их глубина max_depth или минимальное требуемое количество образцов для рассмотрения разделения min_samples_split).
Примеры
Многоклассовые деревья решений с бустингом AdaBoost показывает производительность AdaBoost на многоклассовой задаче.
Двухклассовый AdaBoost показывает границу решения и значения функции решения для нелинейно разделимой двухклассовой задачи с использованием AdaBoost-SAMME.
Регрессия решающего дерева с AdaBoost демонстрирует регрессию с алгоритмом AdaBoost.R2.
Ссылки