2.6. Оценка ковариации#

Многие статистические задачи требуют оценки ковариационной матрицы популяции, которую можно рассматривать как оценку формы диаграммы рассеяния набора данных. Чаще всего такая оценка должна выполняться на выборке, свойства которой (размер, структура, однородность) сильно влияют на качество оценки. sklearn.covariance пакет предоставляет инструменты для точной оценки ковариационной матрицы популяции в различных условиях.

Мы предполагаем, что наблюдения независимы и одинаково распределены (i.i.d.).

2.6.1. Эмпирическая ковариация#

Известно, что ковариационная матрица набора данных хорошо аппроксимируется классической оценка максимального правдоподобия (или «эмпирическая ковариация»), при условии, что количество наблюдений достаточно велико по сравнению с количеством признаков (переменных, описывающих наблюдения). Более точно, оценка максимального правдоподобия выборки является асимптотически несмещённой оценкой соответствующей ковариационной матрицы генеральной совокупности.

Эмпирическая ковариационная матрица выборки может быть вычислена с использованием empirical_covariance функция пакета, или путем обучения EmpiricalCovariance объект к выборке данных с EmpiricalCovariance.fit метода. Обратите внимание, что результаты зависят от того, центрированы ли данные, поэтому может потребоваться использовать assume_centered параметр точно. Более точно, если assume_centered=True, тогда все признаки в обучающем и тестовом наборах должны иметь нулевое среднее. Если нет, оба должны быть центрированы пользователем, или assume_centered=False должен использоваться.

Примеры

2.6.2. Сжатая ковариация#

2.6.2.1. Базовое сжатие#

Несмотря на то, что это асимптотически несмещенная оценка ковариационной матрицы, оценка максимального правдоподобия не является хорошей оценкой собственных значений ковариационной матрицы, поэтому матрица точности, полученная из её обращения, не точна. Иногда даже случается, что эмпирическая ковариационная матрица не может быть обращена по численным причинам. Чтобы избежать такой проблемы обращения, было введено преобразование эмпирической ковариационной матрицы: shrinkage.

В scikit-learn это преобразование (с пользовательским коэффициентом сжатия) может быть непосредственно применено к предварительно вычисленной ковариации с помощью shrunk_covariance метод. Также, сжатая оценка ковариации может быть подогнана к данным с помощью ShrunkCovariance объект и его ShrunkCovariance.fit метод. Опять же, результаты зависят от того, центрированы ли данные, поэтому может потребоваться использовать assume_centered параметр точно.

Математически это сжатие состоит в уменьшении отношения между наименьшим и наибольшим собственными значениями эмпирической ковариационной матрицы. Это можно сделать простым смещением каждого собственного значения на заданное смещение, что эквивалентно нахождению l2-штрафованного оценщика максимального правдоподобия ковариационной матрицы. На практике сжатие сводится к простому выпуклому преобразованию: \(\Sigma_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id\).

Выбор степени сжатия, \(\alpha\) сводится к установке компромисса между смещением и дисперсией и обсуждается ниже.

Примеры

2.6.2.2. сжатие Ледойта-Вольфа#

В своей статье 2004 года [1], O. Ledoit и M. Wolf предлагают формулу для вычисления оптимального коэффициента сжатия \(\alpha\) который минимизирует среднеквадратичную ошибку между оцененной и реальной ковариационной матрицей.

Оценщик ковариационной матрицы Ледойта-Вольфа может быть вычислен на выборке с помощью ledoit_wolf функция от sklearn.covariance пакет, или его можно получить другим способом, настроив LedoitWolf объект к тому же образцу.

Примечание

Случай, когда ковариационная матрица популяции изотропна

Важно отметить, что когда количество образцов значительно больше, чем количество признаков, можно ожидать, что сжатие не будет необходимым. Интуиция здесь в том, что если ковариация генеральной совокупности имеет полный ранг, то при увеличении количества образцов выборочная ковариация также станет положительно определенной. В результате сжатие не потребуется, и метод должен автоматически это делать.

Однако это не так в процедуре Ледойта-Вольфа, когда ковариация генеральной совокупности оказывается кратной единичной матрице. В этом случае оценка сжатия Ледойта-Вольфа приближается к 1 с увеличением количества выборок. Это указывает, что оптимальная оценка ковариационной матрицы в смысле Ледойта-Вольфа кратна единичной матрице. Поскольку ковариация генеральной совокупности уже кратна единичной матрице, решение Ледойта-Вольфа действительно является разумной оценкой.

Примеры

Ссылки

2.6.2.3. Oracle Approximating Shrinkage#

В предположении, что данные распределены по Гауссу, Чен и др. [2] вывел формулу, направленную на выбор коэффициента сжатия, который дает меньшую среднеквадратичную ошибку, чем формула Ледойта и Вольфа. Полученный оценщик известен как Oracle Shrinkage Approximating estimator ковариации.

Оценщик OAS ковариационной матрицы может быть вычислен на выборке с помощью oas функция от sklearn.covariance пакете, или его можно получить, обучив OAS объект к тому же образцу.

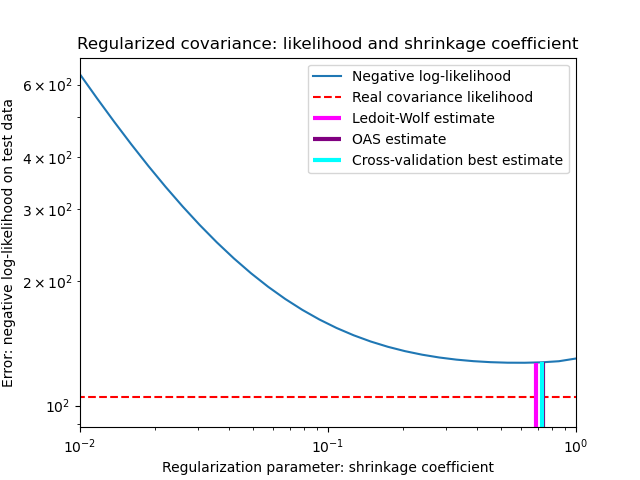
../_images/sphx_glr_plot_covariance_estimation_001.png

Компромисс смещения-дисперсии при установке сжатия: сравнение выбора оценщиков Ledoit-Wolf и OAS#

Ссылки

Примеры

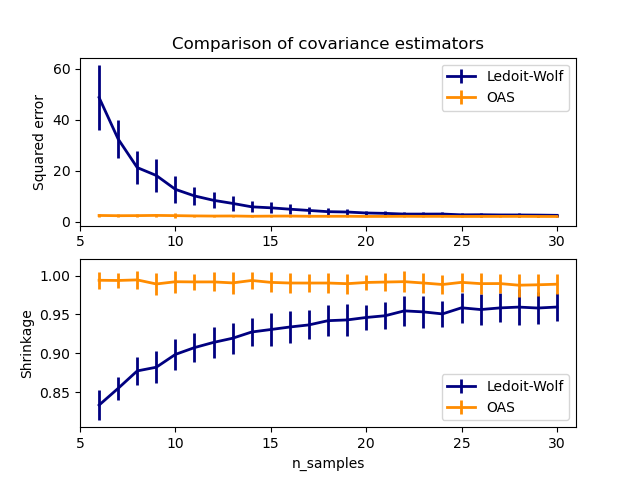
../_images/sphx_glr_plot_lw_vs_oas_001.png

2.6.3. Разреженная обратная ковариация#

Обратная матрица ковариационной матрицы, часто называемая матрицей точности, пропорциональна матрице частных корреляций. Она дает отношение частичной независимости. Другими словами, если два признака независимы условно относительно других, соответствующий коэффициент в матрице точности будет равен нулю. Вот почему имеет смысл оценивать разреженную матрицу точности: оценка ковариационной матрицы лучше обусловлена путем изучения отношений независимости из данных. Это известно как выбор ковариации.

В ситуации с малыми выборками, в которой n_samples имеет порядок n_features или меньше, разреженные оценки обратной ковариации обычно работают лучше, чем оценки сжатой ковариации. Однако в противоположной ситуации или для сильно коррелированных данных они могут быть численно неустойчивыми. Кроме того, в отличие от оценок сжатия, разреженные оценки способны восстанавливать внедиагональную структуру.

The GraphicalLasso оценщик использует штраф l1 для обеспечения разреженности матрицы точности: чем выше его alpha параметра, тем более разреженной будет матрица точности. Соответствующая GraphicalLassoCV объект использует кросс-валидацию для автоматической установки alpha параметр.

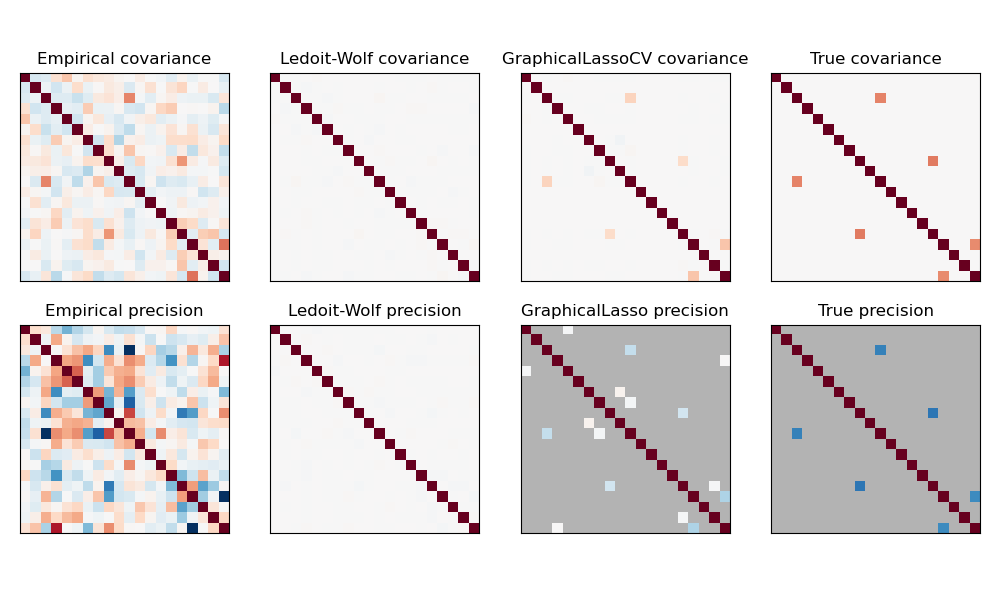
../_images/sphx_glr_plot_sparse_cov_001.png

Сравнение оценок ковариационной и прецизионной матриц методом максимального правдоподобия, сжатия и разреженных оценок в условиях очень малых выборок.#

Примечание

Восстановление структуры

Восстановление графической структуры из корреляций в данных — это сложная задача. Если вы заинтересованы в таком восстановлении, помните, что:

  • Восстановление проще из корреляционной матрицы, чем из ковариационной матрицы: стандартизируйте ваши наблюдения перед запуском GraphicalLasso

  • Если в базовом графе есть узлы со значительно большим количеством связей, чем в среднем по узлам, алгоритм пропустит некоторые из этих связей.

  • Если количество ваших наблюдений невелико по сравнению с количеством ребер в вашем базовом графе, вы не восстановите его.

  • Даже если вы находитесь в благоприятных условиях восстановления, параметр альфа, выбранный с помощью перекрестной проверки (например, с использованием GraphicalLassoCV объект) приведёт к выбору слишком многих рёбер. Однако соответствующие рёбра будут иметь больший вес, чем нерелевантные.

Математическая формулировка следующая:

\[\hat{K} = \mathrm{argmin}_K \big( \mathrm{tr} S K - \mathrm{log} \mathrm{det} K + \alpha \|K\|_1 \big)\]

Где \(K\) это матрица точности, которую нужно оценить, и \(S\) является выборочной ковариационной матрицей. \(\|K\|_1\) является суммой абсолютных значений внедиагональных коэффициентов \(K\). Алгоритм, используемый для решения этой проблемы, — это алгоритм GLasso из статьи Friedman 2008 Biostatistics. Это тот же алгоритм, что и в R glasso пакет.

Примеры

Ссылки

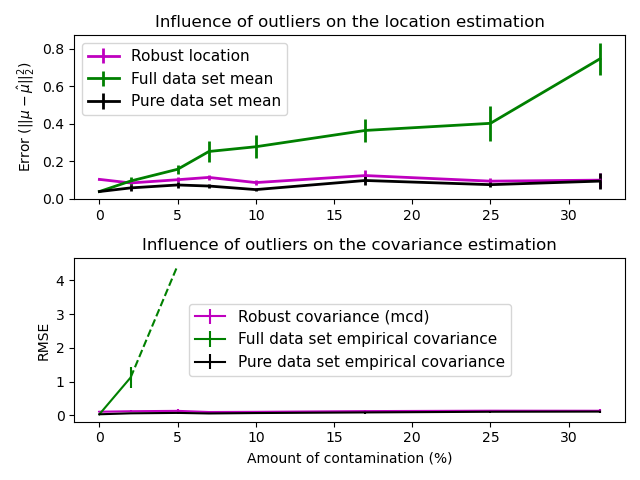
2.6.4. Робастная оценка ковариации#

Реальные наборы данных часто подвержены ошибкам измерений или записи. Регулярные, но необычные наблюдения также могут появляться по разным причинам. Наблюдения, которые очень необычны, называются выбросами. Эмпирический оценщик ковариации и оценщики сжатой ковариации, представленные выше, очень чувствительны к наличию выбросов в данных. Поэтому следует использовать устойчивые оценщики ковариации для оценки ковариации реальных наборов данных. Альтернативно, устойчивые оценщики ковариации могут использоваться для обнаружения выбросов и отбрасывания/понижения веса некоторых наблюдений в соответствии с дальнейшей обработкой данных.

The sklearn.covariance пакет реализует робастный оценщик ковариации, Минимальный Ковариационный Детерминант [3].

2.6.4.1. Минимальный определитель ковариации#

Оценщик минимального ковариационного определителя — это робастный оценщик ковариации набора данных, представленный P.J. Rousseeuw в [3]. Идея состоит в том, чтобы найти заданную долю (h) «хороших» наблюдений, которые не являются выбросами, и вычислить их эмпирическую ковариационную матрицу. Затем эта эмпирическая ковариационная матрица масштабируется для компенсации выполненного выбора наблюдений («этап согласованности»). Вычислив оценщик минимального ковариационного определителя, можно присвоить веса наблюдениям в соответствии с их расстоянием Махаланобиса, что приводит к перевзвешенной оценке ковариационной матрицы набора данных («этап перевзвешивания»).

Руссеув и Ван Дриссен [4] разработал алгоритм FastMCD для вычисления минимального определителя ковариации. Этот алгоритм используется в scikit-learn при подгонке объекта MCD к данным. Алгоритм FastMCD также вычисляет устойчивую оценку местоположения набора данных одновременно.

Сырые оценки доступны как raw_location_ и raw_covariance_ атрибуты MinCovDet объект оценки устойчивой ковариации.

Ссылки

Примеры

Влияние выбросов на оценки местоположения и ковариации

Разделение нормальных объектов от выбросов с использованием расстояния Махаланобиса

robust_vs_emp

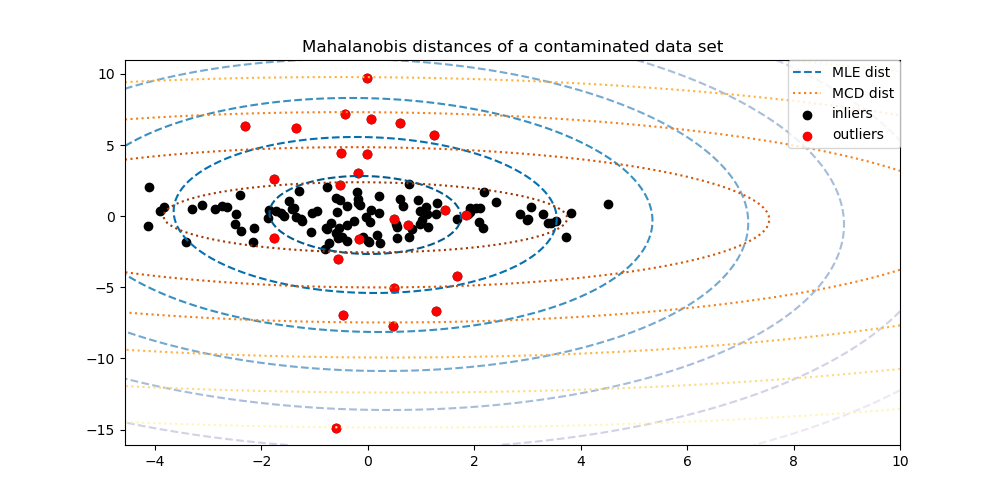
mahalanobis