1.17. 3.2.4.1. Указание целевой метрики#

Предупреждение

Эта реализация не предназначена для крупномасштабных приложений. В частности, scikit-learn не поддерживает GPU. Для более быстрых реализаций на GPU, а также фреймворков, предлагающих гораздо больше гибкости для построения архитектур глубокого обучения, см. Связанные проекты.

1.17.1. Многослойный перцептрон#

Многослойный перцептрон (MLP) является алгоритмом обучения с учителем, который изучает функцию \(f: R^m \rightarrow R^o\) путем обучения на наборе данных, где \(m\) является количеством измерений для входа и \(o\) это количество измерений для вывода. Учитывая набор признаков \(X = \{x_1, x_2, ..., x_m\}\) и цель \(y\), он может изучать нелинейный аппроксиматор функции для классификации или регрессии. Он отличается от логистической регрессии тем, что между входным и выходным слоем может быть один или несколько нелинейных слоев, называемых скрытыми слоями. На рисунке 1 показан MLP с одним скрытым слоем и скалярным выходом.

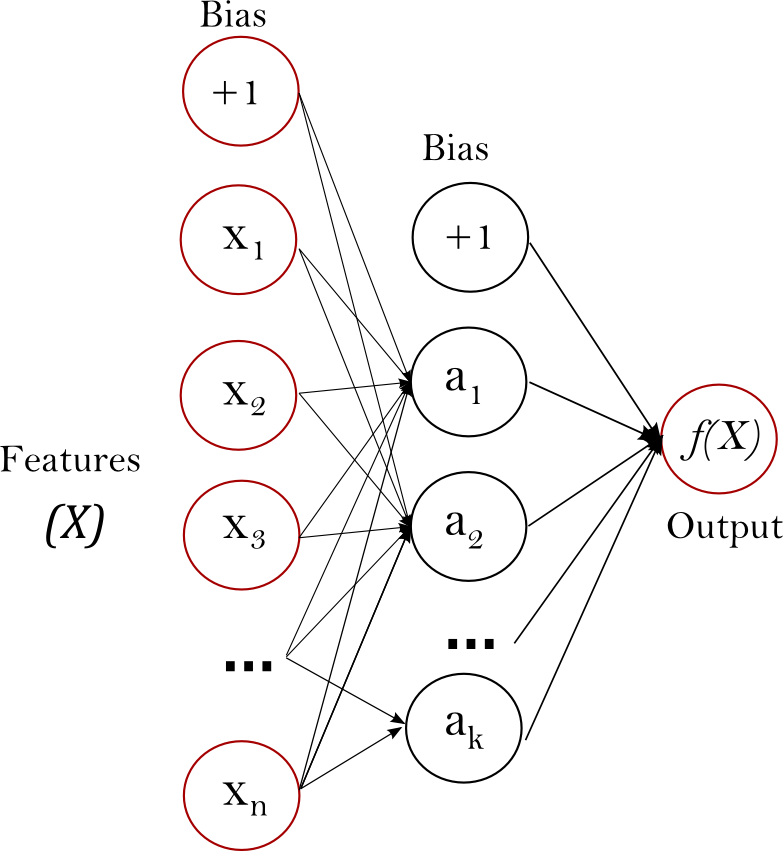
../_images/multilayerperceptron_network.png — **Рисунок 1: MLP с одним скрытым слоем.**#

Самый левый слой, известный как входной слой, состоит из набора нейронов \(\{x_i | x_1, x_2, ..., x_m\}\) представляющие входные признаки. Каждый нейрон в скрытом слое преобразует значения из предыдущего слоя с помощью взвешенной линейной суммы \(w_1x_1 + w_2x_2 + ... + w_mx_m\), за которым следует нелинейная функция активации \(g(\cdot):R \rightarrow R\) - как гиперболический тангенс. Выходной слой получает значения от последнего скрытого слоя и преобразует их в выходные значения.

Модуль содержит публичные атрибуты coefs_ и intercepts_. coefs_ представляет собой список весовых матриц, где весовая матрица с индексом \(i\) представляет веса между слоем \(i\) и слой \(i+1\). intercepts_ является списком векторов смещения, где вектор по индексу \(i\) представляет значения смещения, добавленные к слою \(i+1\).

1.17.2. Классификация#

Класс MLPClassifier implements a multi-layer perceptron (MLP) algorithm that trains using Обратное распространение ошибки.

MLP обучается на двух массивах: массив X размером (n_samples, n_features), который содержит обучающие выборки, представленные как векторы признаков с плавающей точкой; и массив y размером (n_samples,), который содержит целевые значения (метки классов) для обучающих выборок:

>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
              solver='lbfgs')

После обучения модель может предсказывать метки для новых выборок:

>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])

MLP может подогнать нелинейную модель к обучающим данным. clf.coefs_ содержит весовые матрицы, составляющие параметры модели:

>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]

В настоящее время, MLPClassifier поддерживает только функцию потерь перекрестной энтропии, которая позволяет оценивать вероятности, запуская predict_proba метод.

MLP обучается с использованием обратного распространения ошибки. Точнее, он обучается с использованием некоторой формы градиентного спуска, а градиенты вычисляются с помощью обратного распространения ошибки. Для классификации он минимизирует функцию потерь перекрёстной энтропии, давая вектор оценок вероятности \(P(y|x)\) на образец \(x\):

>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967e-04, 9.998e-01],
       [1.967e-04, 9.998e-01]])

MLPClassifier поддерживает многоклассовую классификацию путём применения Softmax в качестве выходной функции.

Кроме того, модель поддерживает многометочная классификация в которой выборка может принадлежать более чем одному классу. Для каждого класса необработанный выход проходит через логистическую функцию. Значения больше или равные 0.5 округляются до 1, иначе в 0. Для прогнозируемого выхода образца индексы, где значение равно 1 представляют назначенные классы этого образца:

>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
              solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])

См. примеры ниже и строку документации MLPClassifier.fit для получения дополнительной информации.

Примеры

Сравнение стохастических стратегий обучения для MLPClassifier
См. Visualization of MLP weights on MNIST для визуализированного представления обученных весов.

1.17.3. Регрессия#

Класс MLPRegressor реализует многослойный перцептрон (MLP), который обучается с использованием обратного распространения без функции активации в выходном слое, что также можно рассматривать как использование тождественной функции в качестве функции активации. Поэтому он использует квадратичную ошибку в качестве функции потерь, а выход представляет собой набор непрерывных значений.

MLPRegressor также поддерживает многомерную регрессию, в которой у образца может быть более одной целевой переменной.

1.17.4. Регуляризация#

Оба MLPRegressor и MLPClassifier используйте параметр alpha для регуляризации (L2-регуляризация), которая помогает избежать переобучения, штрафуя веса с большими величинами. Следующий график показывает изменяющуюся решающую функцию со значением альфа.

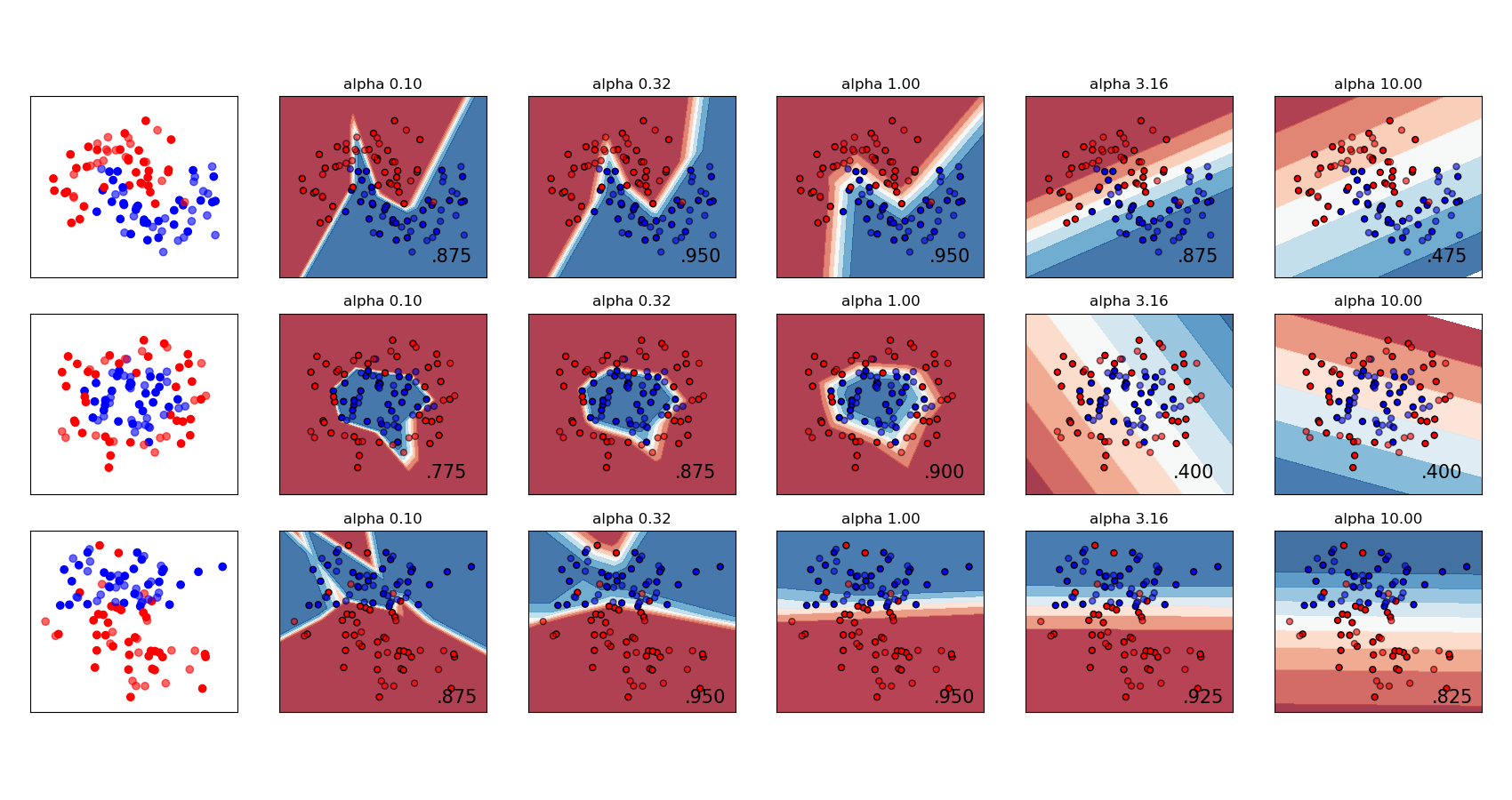
../_images/sphx_glr_plot_mlp_alpha_001.png

Смотрите примеры ниже для дополнительной информации.

Примеры

Изменение регуляризации в многослойном перцептроне

1.17.5. Алгоритмы#

MLP обучается с использованием Стохастический градиентный спуск, Адам, или L-BFGS. Стохастический градиентный спуск (SGD) обновляет параметры с использованием градиента функции потерь по отношению к параметру, который нуждается в адаптации, т.е.

\[w \leftarrow w - \eta \left[\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial Loss}{\partial w}\right]\]

где \(\eta\) — это скорость обучения, которая контролирует размер шага в поиске по пространству параметров. \(Loss\) является функцией потерь, используемой для сети.

Более подробную информацию можно найти в документации SGD

Adam похож на SGD в том смысле, что это стохастический оптимизатор, но он может автоматически регулировать величину обновления параметров на основе адаптивных оценок моментов низшего порядка.

При использовании SGD или Adam обучение поддерживает онлайн-обучение и обучение мини-пакетами.

L-BFGS — это решатель, который аппроксимирует матрицу Гессе, представляющую вторую частную производную функции. Далее он аппроксимирует обратную матрицу Гессе для выполнения обновлений параметров. Реализация использует версию Scipy L-BFGS.

Если выбранный решатель — 'L-BFGS', обучение не поддерживает онлайн- или мини-пакетное обучение.

1.17.6. Сложность#

Предположим, есть \(n\) обучающие образцы, \(m\) признаки, \(k\) скрытых слоев, каждый из которых содержит \(h\) нейроны - для простоты, и \(o\) выходных нейронов. Временная сложность обратного распространения равна \(O(i \cdot n \cdot (m \cdot h + (k - 1) \cdot h \cdot h + h \cdot o))\), где \(i\) это количество итераций. Поскольку обратное распространение имеет высокую временную сложность, рекомендуется начинать с меньшего количества скрытых нейронов и нескольких скрытых слоев для обучения.

Математическая формулировка#

Для заданного набора обучающих примеров \(\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\) где \(x_i \in \mathbf{R}^n\) и \(y_i \in \{0, 1\}\), однослойный MLP с одним скрытым нейроном изучает функцию \(f(x) = W_2 g(W_1^T x + b_1) + b_2\) где \(W_1 \in \mathbf{R}^m\) и \(W_2, b_1, b_2 \in \mathbf{R}\) являются параметрами модели. \(W_1, W_2\) представляют веса входного слоя и скрытого слоя соответственно; и \(b_1, b_2\) представляют смещение, добавленное к скрытому слою и выходному слою соответственно. \(g(\cdot) : R \rightarrow R\) — это функция активации, установленная по умолчанию как гиперболический тангенс. Она задается как,

\[g(z)= \frac{e^z-e^{-z}}{e^z+e^{-z}}\]

Для бинарной классификации, \(f(x)\) проходит через логистическую функцию \(g(z)=1/(1+e^{-z})\) для получения выходных значений между нулём и единицей. Порог, установленный на 0.5, будет присваивать образцы с выходными значениями больше или равными 0.5 положительному классу, а остальные - отрицательному.

Если классов больше двух, \(f(x)\) сам по себе будет вектором размера (n_classes,). Вместо прохождения через логистическую функцию, он проходит через функцию softmax, которая записывается как,

\[\text{softmax}(z)_i = \frac{\exp(z_i)}{\sum_{l=1}^k\exp(z_l)}\]

где \(z_i\) представляет \(i\) элемент входа в softmax, который соответствует классу \(i\), и \(K\) это количество классов. Результат — вектор, содержащий вероятности того, что образец \(x\) принадлежит каждому классу. Выходом является класс с наибольшей вероятностью.

В регрессии выход остаётся как \(f(x)\); следовательно, выходная активационная функция — это просто тождественная функция.

MLP использует различные функции потерь в зависимости от типа задачи. Функция потерь для классификации — это средняя перекрестная энтропия, которая в бинарном случае задается как,

\[Loss(\hat{y},y,W) = -\dfrac{1}{n}\sum_{i=0}^n(y_i \ln {\hat{y_i}} + (1-y_i) \ln{(1-\hat{y_i})}) + \dfrac{\alpha}{2n} ||W||_2^2\]

где \(\alpha ||W||_2^2\) является членом L2-регуляризации (также называемым штрафом), который штрафует сложные модели; и \(\alpha > 0\) является неотрицательным гиперпараметром, который контролирует величину штрафа.

Для регрессии MLP использует функцию потерь среднеквадратичной ошибки; записывается как,

\[Loss(\hat{y},y,W) = \frac{1}{2n}\sum_{i=0}^n||\hat{y}_i - y_i ||_2^2 + \frac{\alpha}{2n} ||W||_2^2\]

Начиная с начальных случайных весов, многослойный перцептрон (MLP) минимизирует функцию потерь, многократно обновляя эти веса. После вычисления потерь обратный проход распространяет их от выходного слоя к предыдущим слоям, предоставляя каждому весовому параметру значение обновления, предназначенное для уменьшения потерь.

При градиентном спуске градиент \(\nabla Loss_{W}\) градиента функции потерь по весам вычисляется и вычитается из \(W\). Более формально это выражается как,

\[W^{i+1} = W^i - \epsilon \nabla {Loss}_{W}^{i}\]

где \(i\) это шаг итерации, и \(\epsilon\) это скорость обучения со значением больше 0.

Алгоритм останавливается, когда достигает предустановленного максимального числа итераций; или когда улучшение потерь ниже определенного небольшого числа.

1.17.7. Советы по практическому использованию#

7.2.2. тот же масштабирование на тестовом наборе для значимых результатов. Вы можете использовать StandardScaler для стандартизации.
```
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> # Don't cheat - fit only on training data
>>> scaler.fit(X_train)
>>> X_train = scaler.transform(X_train)
>>> # apply same transformation to test data
>>> X_test = scaler.transform(X_test)
```
Альтернативный и рекомендуемый подход — использовать StandardScaler в Pipeline
Поиск разумного параметра регуляризации \(\alpha\) лучше всего выполнять с помощью GridSearchCV, обычно в диапазоне 10.0 ** -np.arange(1, 7).
Эмпирически мы наблюдали, что L-BFGS сходится быстрее и с лучшими решениями на небольших наборах данных. Однако для относительно больших наборов данных Adam очень устойчив. Обычно сходится быстро и дает довольно хорошую производительность. SGD с импульсом или импульсом Нестерова, с другой стороны, может работать лучше, чем эти два алгоритма, если скорость обучения правильно настроена.

1.17.8. Больше контроля с warm_start#

Если вам нужен больший контроль над критериями остановки или скоростью обучения в SGD, или вы хотите осуществлять дополнительный мониторинг, используйте warm_start=True и max_iter=1 и самостоятельная итерация может быть полезной:

>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
...     clf.fit(X, y)
...     # additional monitoring / inspection
MLPClassifier(...