7.7. Аппроксимация ядра#

Этот подмодуль содержит функции, которые аппроксимируют отображения признаков, соответствующие определенным ядрам, как они используются, например, в машинах опорных векторов (см. Метод опорных векторов). Следующие функции признаков выполняют нелинейные преобразования входных данных, которые могут служить основой для линейной классификации или других алгоритмов.

Преимущество использования приближенных явных отображений признаков по сравнению с ядерный трюк, который использует отображения признаков неявно, заключается в том, что явные отображения могут быть лучше подходят для онлайн-обучения и могут значительно снизить стоимость обучения на очень больших наборах данных. Стандартные ядерные SVM плохо масштабируются на большие наборы данных, но используя приближенное ядерное отображение, можно использовать гораздо более эффективные линейные SVM. В частности, комбинация приближений ядерных отображений с SGDClassifier может сделать нелинейное обучение на больших наборах данных возможным.

Поскольку эмпирических работ с использованием приближенных вложений не так много, рекомендуется по возможности сравнивать результаты с точными методами ядер.

Смотрите также

Полиномиальная регрессия: расширение линейных моделей с базисными функциями для точного полиномиального преобразования.

7.7.1. Метод Нистрёма для аппроксимации ядра#

Метод Нистрёма, реализованный в Nystroem является общим методом для приближений пониженного ранга ядер. Это достигается путем субдискретизации без замены строк/столбцов данных, на которых вычисляется ядро. В то время как вычислительная сложность точного метода составляет \(\mathcal{O}(n^3_{\text{samples}})\), сложность аппроксимации \(\mathcal{O}(n^2_{\text{components}} \cdot n_{\text{samples}})\), где можно установить \(n_{\text{components}} \ll n_{\text{samples}}\) без значительного снижения производительности [WS2001].

Мы можем построить собственное разложение матрицы ядра \(K\), на основе признаков данных, а затем разделить их на выборочные и невыборочные точки данных.

\[\begin{split}K = U \Lambda U^T = \begin{bmatrix} U_1 \\ U_2\end{bmatrix} \Lambda \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}^T = \begin{bmatrix} U_1 \Lambda U_1^T & U_1 \Lambda U_2^T \\ U_2 \Lambda U_1^T & U_2 \Lambda U_2^T \end{bmatrix} \equiv \begin{bmatrix} K_{11} & K_{12} \\ K_{21} & K_{22} \end{bmatrix}\end{split}\]

где:

\(U\) является ортонормированным
\(\Lambda\) является диагональной матрицей собственных значений
\(U_1\) является ортонормированной матрицей выбранных образцов
\(U_2\) является ортонормированной матрицей выборок, которые не были выбраны

Учитывая, что \(U_1 \Lambda U_1^T\) может быть получена ортонормированием матрицы \(K_{11}\), и \(U_2 \Lambda U_1^T\) может быть оценен (а также его транспонирование), единственный оставшийся термин для разъяснения — \(U_2 \Lambda U_2^T\). Для этого мы можем выразить это через уже вычисленные матрицы:

\[\begin{split}\begin{align} U_2 \Lambda U_2^T &= \left(K_{21} U_1 \Lambda^{-1}\right) \Lambda \left(K_{21} U_1 \Lambda^{-1}\right)^T \\&= K_{21} U_1 (\Lambda^{-1} \Lambda) \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} U_1 \Lambda^{-1} U_1^T K_{21}^T \\&= K_{21} K_{11}^{-1} K_{21}^T \\&= \left( K_{21} K_{11}^{-\frac12} \right) \left( K_{21} K_{11}^{-\frac12} \right)^T .\end{align}\end{split}\]

Во время fit, класс Nystroem оценивает базис \(U_1\), и вычисляет константу нормализации, \(K_{11}^{-\frac12}\). Позже, во время transform, матрица ядра определяется между базисом (заданным components_ атрибут) и новые точки данных, X. Эта матрица затем умножается на normalization_ матрица для конечного результата.

По умолчанию Nystroem использует rbf ядро, но оно может использовать любую функцию ядра или предварительно вычисленную матрицу ядра. Количество используемых выборок — которое также является размерностью вычисляемых признаков — задается параметром n_components.

Примеры

См. пример под названием Инженерия временных признаков, который показывает эффективный конвейер машинного обучения, использующий Nystroem ядро.
См. Аппроксимация явного отображения признаков для RBF-ядер для сравнения Nystroem ядро с RBFSampler.

7.7.2. Ядро радиальной базисной функции#

The RBFSampler строит приближенное отображение для радиального базисного ядра, также известного как Random Kitchen Sinks [RR2007]. Это преобразование может быть использовано для явного моделирования карты ядра перед применением линейного алгоритма, например, линейного SVM:

>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0

Отображение основано на приближении Монте-Карло к значениям ядра. fit функция выполняет выборку методом Монте-Карло, тогда как transform метод выполняет отображение данных. Из-за присущей процессу случайности результаты могут различаться между разными вызовами fit функция.

The fit функция принимает два аргумента: n_components, что является целевой размерностью преобразования признаков, и gamma, параметр RBF-ядра. Более высокое n_components приведёт к лучшему приближению ядра и даст результаты, более похожие на те, что получены с помощью ядерного SVM. Обратите внимание, что «подгонка» функции признаков фактически не зависит от данных, переданных в fit функция. Используется только размерность данных. Подробности о методе можно найти в [RR2007].

Для заданного значения n_components RBFSampler часто менее точен, так как Nystroem. RBFSampler дешевле вычислять, что делает использование больших пространств признаков более эффективным.

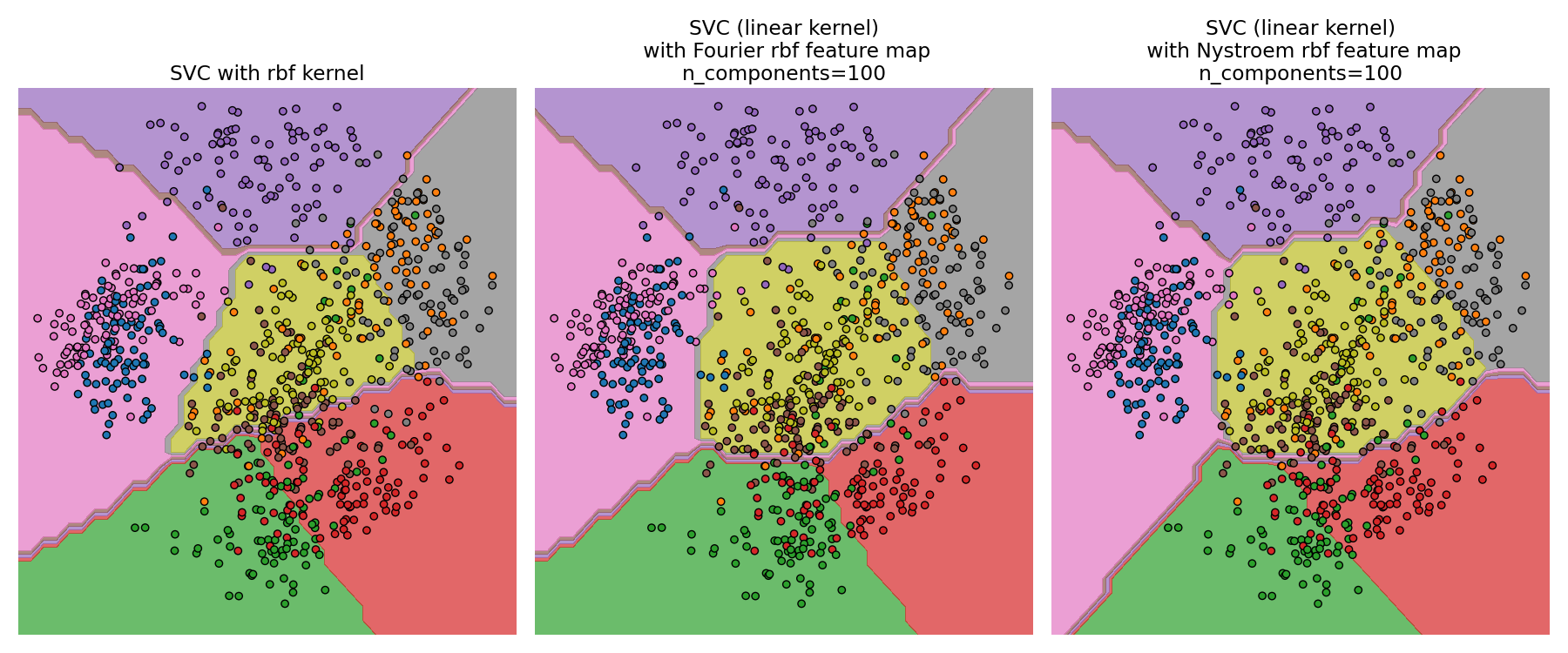
../_images/sphx_glr_plot_kernel_approximation_002.png — Сравнение точного RBF-ядра (слева) с аппроксимацией (справа)#

Примеры

См. Аппроксимация явного отображения признаков для RBF-ядер для сравнения Nystroem ядро с RBFSampler.

7.7.3. Аддитивное ядро хи-квадрат#

Аддитивное хи-квадрат ядро — это ядро для гистограмм, часто используемое в компьютерном зрении.

Аддитивное хи-квадрат ядро, используемое здесь, задаётся как

\[k(x, y) = \sum_i \frac{2x_iy_i}{x_i+y_i}\]

Это не совсем то же самое, что sklearn.metrics.pairwise.additive_chi2_kernel. Авторы [VZ2010] предпочитайте версию выше, так как она всегда положительно определена. Поскольку ядро аддитивно, можно обрабатывать все компоненты \(x_i\) отдельно для встраивания. Это позволяет сэмплировать преобразование Фурье через регулярные интервалы вместо аппроксимации с использованием сэмплирования Монте-Карло.

Класс AdditiveChi2Sampler реализует это покомпонентное детерминированное сэмплирование. Каждый компонент сэмплируется \(n\) раз, давая \(2n+1\) размерностей на входное измерение (кратность двум происходит из действительной и мнимой части преобразования Фурье). В литературе \(n\) обычно выбирается равным 1 или 2, преобразуя набор данных до размера n_samples * 5 * n_features (в случае \(n=2\)).

Приближенное отображение признаков, предоставляемое AdditiveChi2Sampler может быть объединен с приближенным отображением признаков, предоставляемым RBFSampler для получения приближенного отображения признаков для экспоненциального хи-квадрат ядра. См. [VZ2010] для деталей и [VVZ2010] для комбинации с RBFSampler.

7.7.4. Асимметричное ядро хи-квадрат#

Асимметричное хи-квадрат ядро задается формулой:

\[k(x,y) = \prod_i \frac{2\sqrt{x_i+c}\sqrt{y_i+c}}{x_i + y_i + 2c}\]

Обладает свойствами, похожими на экспоненцированное хи-квадрат ядро, часто используемое в компьютерном зрении, но позволяет использовать простое Монте-Карло приближение карты признаков.

Использование SkewedChi2Sampler совпадает с использованием, описанным выше для RBFSampler. Единственное различие заключается в свободном параметре, который называется \(c\). Для обоснования этого отображения и математических деталей см. [LS2010].

7.7.5. Полиномиальная аппроксимация ядра через тензорный скетч#

The полиномиальное ядро является популярным типом функции ядра, заданной как:

\[k(x, y) = (\gamma x^\top y +c_0)^d\]

где:

x, y являются входными векторами
d является степенью ядра

Интуитивно, пространство признаков полиномиального ядра степени d состоит из всех возможных степеней-d произведения между входными признаками, что позволяет алгоритмам обучения, использующим это ядро, учитывать взаимодействия между признаками.

TensorSketch [PP2013] метод, реализованный в PolynomialCountSketch, является масштабируемым, независимым от входных данных методом аппроксимации полиномиального ядра. Он основан на концепции Count sketch [WIKICS] [CCF2002] , метод уменьшения размерности, аналогичный хешированию признаков, который вместо этого использует несколько независимых хеш-функций. TensorSketch получает Count Sketch внешнего произведения двух векторов (или вектора с самим собой), который можно использовать как приближение пространства признаков полиномиального ядра. В частности, вместо явного вычисления внешнего произведения TensorSketch вычисляет Count Sketch векторов, а затем использует полиномиальное умножение через быстрое преобразование Фурье для вычисления Count Sketch их внешнего произведения.

Удобно, что фаза обучения TensorSketch состоит просто из инициализации некоторых случайных переменных. Таким образом, она не зависит от входных данных, т.е. зависит только от количества входных признаков, но не от значений данных. Кроме того, этот метод может преобразовывать выборки в \(\mathcal{O}(n_{\text{samples}}(n_{\text{features}} + n_{\text{components}} \log(n_{\text{components}})))\) time, where \(n_{\text{components}}\) является желаемой размерностью выхода, определяемой n_components.

Примеры

Масштабируемое обучение с полиномиальной аппроксимацией ядра

7.7.6. Математические детали#

Методы ядра, такие как метод опорных векторов или ядерный метод главных компонент, основаны на свойстве воспроизводящих гильбертовых пространств ядер. Для любой положительно определённой ядерной функции \(k\) (так называемое ядро Мерсера), гарантируется, что существует отображение \(\phi\) в пространство Гильберта \(\mathcal{H}\), так что

\[k(x,y) = \langle \phi(x), \phi(y) \rangle\]

Где \(\langle \cdot, \cdot \rangle\) обозначает скалярное произведение в гильбертовом пространстве.

Если алгоритм, такой как линейный метод опорных векторов или PCA, полагается только на скалярное произведение точек данных \(x_i\), можно использовать значение \(k(x_i, x_j)\), что соответствует применению алгоритма к отображённым точкам данных \(\phi(x_i)\). Преимущество использования \(k\) заключается в том, что отображение \(\phi\) никогда не вычисляется явно, что позволяет работать с произвольно большими признаками (даже бесконечными).

Один недостаток методов ядра заключается в том, что может потребоваться хранить множество значений ядра \(k(x_i, x_j)\) во время оптимизации. Если классификатор с ядром применяется к новым данным \(y_j\), \(k(x_i, y_j)\) должно быть вычислено для выполнения предсказаний, возможно, для многих различных \(x_i\) в обучающем наборе.

Классы в этом подмодуле позволяют аппроксимировать вложение \(\phi\), тем самым работая явно с представлениями \(\phi(x_i)\), что устраняет необходимость применения ядра или хранения обучающих примеров.

Ссылки

[WS2001]

«Использование метода Нюстрёма для ускорения ядерных машин» Williams, C.K.I.; Seeger, M. - 2001.

[RR2007] (1,2)

“Случайные признаки для крупномасштабных ядерных машин” Rahimi, A. и Recht, B. - Advances in neural information processing 2007,

[LS2010]

«Случайные аппроксимации Фурье для асимметричных мультипликативных гистограммных ядер» Ли, Ф., Ионеску, К., и Сминчисеску, К. - Pattern Recognition, DAGM 2010, Lecture Notes in Computer Science.

[VZ2010] (1,2)

«Эффективные аддитивные ядра через явные отображения признаков» Vedaldi, A. and Zisserman, A. - Computer Vision and Pattern Recognition 2010

[VVZ2010]

'Generalized RBF feature maps for Efficient Detection' Vempati, S. и Vedaldi, A. и Zisserman, A. и Jawahar, CV - 2010

[PP2013]