1.14. Полу-контролируемое обучение

Полу-контролируемое обучение — это ситуация, когда в обучающих данных некоторые образцы не размечены. Полу-обучаемые оценщики в sklearn.semi_supervised могут использовать эти дополнительные немаркированные данные, чтобы лучше уловить форму лежащего в основе распределения данных и лучше обобщать на новые выборки. Эти алгоритмы могут хорошо работать, когда у нас очень мало маркированных точек и много немаркированных точек.

Неразмеченные записи в y

Важно присвоить идентификатор неразмеченным точкам вместе с размеченными данными при обучении модели с помощью fit метода. Идентификатор, который использует эта реализация, — целочисленное значение \(-1\). Обратите внимание, что для строковых меток тип данных y должен быть объектом, чтобы он мог содержать как строки, так и целые числа.

Примечание

Полу-контролируемые алгоритмы должны делать предположения о распределении набора данных для достижения прироста производительности. См. здесь для получения дополнительной информации.

Примеры

• Полу-контролируемая классификация на текстовом наборе данных

1.14.1. Самообучение

Эта реализация самообучения основана на методе Яровского [1] алгоритм. Используя этот алгоритм, заданный контролируемый классификатор может функционировать как полуконтролируемый классификатор, позволяя ему обучаться на немаркированных данных.

SelfTrainingClassifier может вызываться с любым классификатором, который реализует predict_proba, передаваемый как параметр estimator. В каждой итерации estimator предсказывает метки для немаркированных образцов и добавляет подмножество этих меток к маркированному набору данных.

Выбор этого подмножества определяется критерием отбора. Этот отбор может быть выполнен с использованием threshold на вероятностях предсказания, или выбором k_best выборки в соответствии с вероятностями предсказания.

Метки, используемые для окончательного обучения, а также итерация, в которой каждый образец был помечен, доступны как атрибуты. Необязательный max_iter параметр указывает, сколько раз цикл выполняется максимум.

The max_iter параметр может быть установлен в None, заставляя алгоритм итерировать, пока все образцы не получат метки или пока в этой итерации не будут выбраны новые образцы.

Примечание

При использовании классификатора с самообучением, калибровка классификатора важно.

Примеры

• Влияние изменения порога для самообучения

• Граница решения полуконтролируемых классификаторов против SVM на наборе данных Iris

Ссылки

[1]

“Независимое разрешение неоднозначности слов, конкурирующее с контролируемыми методами” David Yarowsky, Proceedings of the 33rd annual meeting on Association for Computational Linguistics (ACL ‘95). Association for Computational Linguistics, Stroudsburg, PA, USA, 189-196.

1.14.2. Распространение меток

Распространение меток обозначает несколько вариаций полуконтролируемых алгоритмов вывода на графах.

Несколько доступных функций в этой модели:

• Используется для задач классификации

• Исходный индекс Фоулкса-Мэллоуза (FMI) предназначался для измерения сходства между двумя результатами кластеризации, что по своей природе является неконтролируемым сравнением. Контролируемая адаптация индекса Фоулкса-Мэллоуза (как реализовано в

scikit-learn предоставляет две модели распространения меток: LabelPropagation и LabelSpreading. Оба работают путем построения графа сходства по всем элементам входного набора данных.

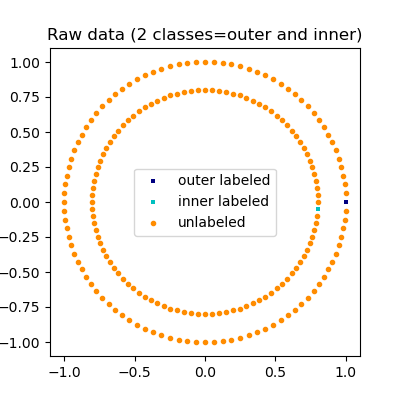
Иллюстрация распространения меток: структура немаркированных наблюдений согласуется со структурой класса, и, таким образом, метка класса может быть распространена на немаркированные наблюдения обучающего набора.

LabelPropagation и LabelSpreading отличаются модификациями матрицы сходства графа и эффектом закрепления на распределения меток. Закрепление позволяет алгоритму изменять вес истинных размеченных данных в некоторой степени. LabelPropagation алгоритм выполняет жёсткое ограничение входных меток, что означает \(\alpha=0\). Этот ограничивающий коэффициент можно ослабить, например, до \(\alpha=0.2\), что означает, что мы всегда сохраним 80 процентов исходного распределения меток, но алгоритм может изменить уверенность в распределении в пределах 20 процентов.

LabelPropagation использует исходную матрицу сходства, построенную из данных без изменений. В отличие от этого, LabelSpreading минимизирует функцию потерь, обладающую свойствами регуляризации, поэтому она часто более устойчива к шуму. Алгоритм итеративно работает с модифицированной версией исходного графа и нормализует веса рёбер путём вычисления нормализованной матрицы Лапласа графа. Эта процедура также используется в Спектральная кластеризация.

Модели распространения меток имеют два встроенных метода ядра. Выбор ядра влияет как на масштабируемость, так и на производительность алгоритмов. Доступны следующие:

• rbf (\(\exp(-\gamma |x-y|^2), \gamma > 0\)). \(\gamma\) задается ключевым словом gamma.

• knn (\(1[x' \in kNN(x)]\)). \(k\) задается ключевым словом n_neighbors.

Ядро RBF создаст полностью связный граф, который представлен в памяти плотной матрицей. Эта матрица может быть очень большой, и в сочетании со стоимостью выполнения полного матричного умножения на каждой итерации алгоритма может привести к неприемлемо долгому времени выполнения. С другой стороны, ядро KNN создаст гораздо более экономную по памяти разреженную матрицу, которая может резко сократить время выполнения.

Примеры

• Граница решения полуконтролируемых классификаторов против SVM на наборе данных Iris

• Распространение меток по кругам: Обучение сложной структуре

• Распространение меток на цифрах: Демонстрация производительности

• Распространение меток цифр: Активное обучение

Ссылки

[2] Yoshua Bengio, Olivier Delalleau, Nicolas Le Roux. In Semi-Supervised Learning (2006), pp. 193-216

[3] Оливье Делалло, Йошуа Бенжио, Николя Ле Ру. Эффективная непараметрическая индукция функций в полуконтролируемом обучении. AISTAT 2005 https://www.gatsby.ucl.ac.uk/aistats/fullpapers/204.pdf