2.5. Разложение сигналов на компоненты (проблемы матричной факторизации)

2.5.1. Метод главных компонент (PCA)

2.5.1.1. Точный PCA и вероятностная интерпретация

PCA используется для разложения многомерного набора данных на набор последовательных ортогональных компонентов, которые объясняют максимальное количество дисперсии. В scikit-learn, PCA реализован как преобразователь объект, который обучается \(n\) компоненты в его fit метод и может использоваться на новых данных для их проекции на эти компоненты.

PCA центрирует, но не масштабирует входные данные для каждого признака перед применением SVD. Необязательный параметр whiten=True позволяет проецировать данные в сингулярное пространство, масштабируя каждый компонент до единичной дисперсии. Это часто полезно, если последующие модели строят сильные предположения об изотропности сигнала: например, это имеет место для машин опорных векторов с RBF-ядром и алгоритма кластеризации K-средних.

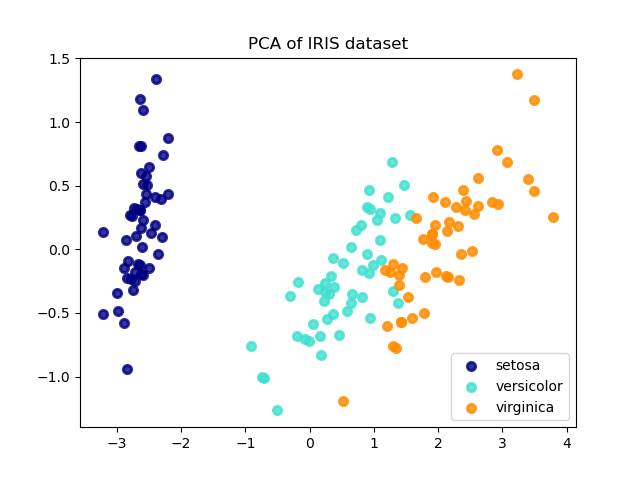
Ниже приведён пример набора данных ирисов, который состоит из 4 признаков, спроецированных на 2 измерения, объясняющих наибольшую дисперсию:

The PCA объект также предоставляет вероятностную интерпретацию PCA, которая может дать правдоподобие данных на основе объясняемой дисперсии. Таким образом, он реализует score метод, который можно использовать в перекрестной проверке:

Примеры

• Анализ главных компонент (PCA) на наборе данных Iris

• Сравнение LDA и PCA 2D проекции набора данных Iris

• Выбор модели с вероятностным PCA и факторным анализом (FA)

2.5.1.2. Инкрементальный PCA

The PCA объект очень полезен, но имеет определённые ограничения для больших наборов данных. Самое большое ограничение — это PCA поддерживает только пакетную обработку, что означает, что все данные для обработки должны помещаться в оперативную память. IncrementalPCA объект использует другую форму обработки и позволяет выполнять частичные вычисления, которые почти точно соответствуют результатам PCA при обработке данных в режиме мини-пакетов. IncrementalPCA позволяет реализовать внеядерный анализ главных компонент либо путем:

• Используя его partial_fit метод на фрагментах данных, последовательно извлекаемых с локального жесткого диска или сетевой базы данных.

• Вызов его метода fit на файле, отображенном в память, с использованием numpy.memmap.

IncrementalPCA хранит только оценки дисперсий компонентов и шума, чтобы обновить explained_variance_ratio_ инкрементально. Вот почему использование памяти зависит от количества образцов в пакете, а не от количества образцов, которые необходимо обработать в наборе данных.

Как в PCA, IncrementalPCA центры, но не масштабирует входные данные для каждого признака перед применением SVD.

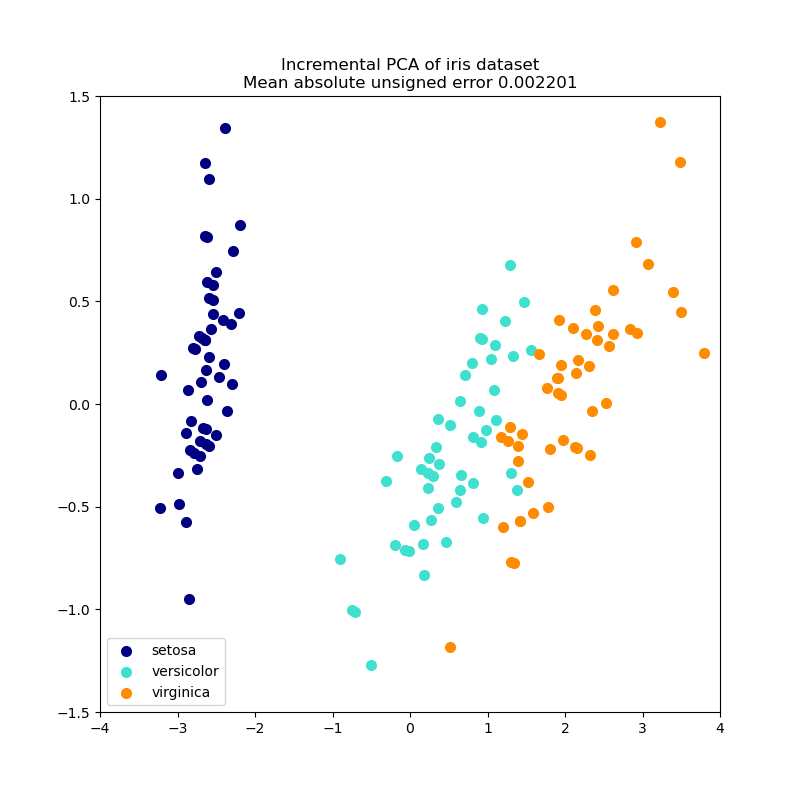
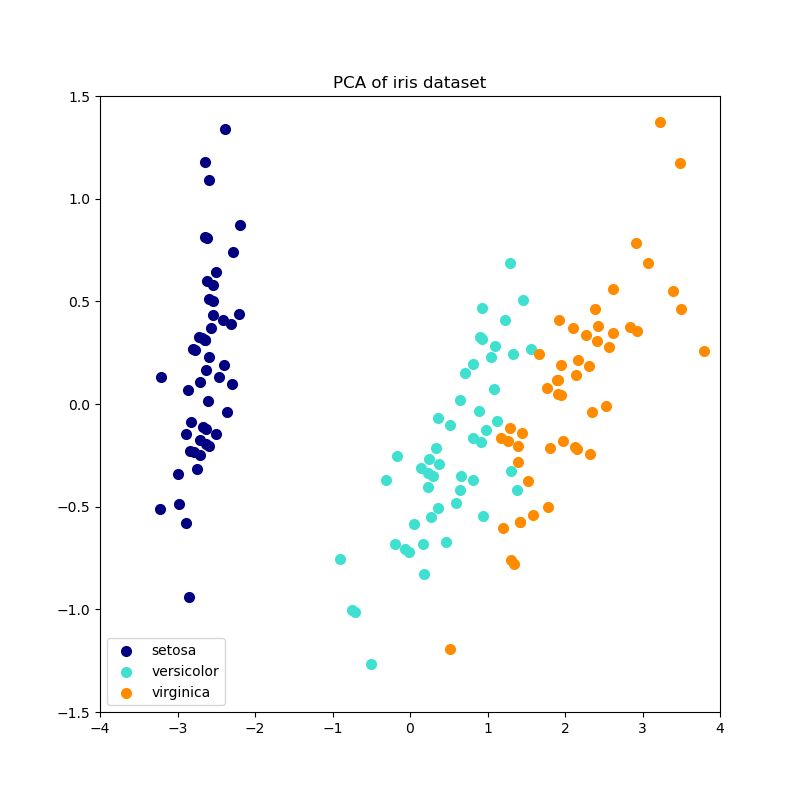
Примеры

• Инкрементальный PCA

2.5.1.3. PCA с использованием рандомизированного SVD

Часто бывает интересно спроецировать данные в пространство меньшей размерности, которое сохраняет большую часть дисперсии, отбрасывая сингулярный вектор компонентов, связанных с меньшими сингулярными значениями.

Например, если мы работаем с 64x64 пиксельными черно-белыми изображениями для распознавания лиц, размерность данных составляет 4096, и обучение машины опорных векторов с RBF-ядром на таких широких данных происходит медленно. Кроме того, мы знаем, что внутренняя размерность данных намного меньше 4096, поскольку все изображения человеческих лиц выглядят примерно одинаково. Образцы лежат на многообразии гораздо меньшей размерности (скажем, около 200, например). Алгоритм PCA может быть использован для линейного преобразования данных с одновременным уменьшением размерности и сохранением большей части объясненной дисперсии.

Класс PCA используется с необязательным параметром svd_solver='randomized' очень полезен в этом случае: поскольку мы собираемся отбросить большинство сингулярных векторов, гораздо эффективнее ограничить вычисления приближённой оценкой сингулярных векторов, которые мы сохраним для фактического выполнения преобразования.

Например, следующие 16 образцов портретов (центрированных вокруг 0.0) из набора данных Olivetti. Справа — первые 16 сингулярных векторов, преобразованных в портреты. Поскольку нам требуются только верхние 16 сингулярных векторов набора данных размером \(n_{samples} = 400\) и \(n_{features} = 64 \times 64 = 4096\), время вычисления менее 1 с:

Если мы отметим \(n_{\max} = \max(n_{\mathrm{samples}}, n_{\mathrm{features}})\) и \(n_{\min} = \min(n_{\mathrm{samples}}, n_{\mathrm{features}})\), временная сложность рандомизированного PCA является \(O(n_{\max}^2 \cdot n_{\mathrm{components}})\) вместо \(O(n_{\max}^2 \cdot n_{\min})\) для точного метода реализованного в PCA.

Объем памяти рандомизированного PCA также пропорционально \(2 \cdot n_{\max} \cdot n_{\mathrm{components}}\) вместо \(n_{\max} \cdot n_{\min}\) для точного метода.

Примечание: реализация inverse_transform в PCA с svd_solver='randomized' не является точным обратным преобразованием transform даже когда whiten=False (по умолчанию).

Примеры

• Пример распознавания лиц с использованием собственных лиц и SVM

• Разложения набора данных Faces

Ссылки

• Алгоритм 4.3 в “Нахождение структуры с помощью случайности: Стохастические алгоритмы для построения приближённых матричных разложений” Halko и др., 2009

• “Реализация рандомизированного алгоритма для анализа главных компонент” A. Szlam et al. 2014

2.5.1.4. Разреженный анализ главных компонент (SparsePCA и MiniBatchSparsePCA)

SparsePCA является вариантом PCA с целью извлечения набора разреженных компонентов, которые лучше всего восстанавливают данные.

Мини-пакетный разреженный PCA (MiniBatchSparsePCA) является вариантом SparsePCA которая быстрее, но менее точна. Повышенная скорость достигается путем итерации по небольшим частям набора признаков для заданного количества итераций.

Метод главных компонент (PCA) имеет недостаток, что компоненты, извлеченные этим методом, имеют исключительно плотные выражения, т.е. они имеют ненулевые коэффициенты при выражении в виде линейных комбинаций исходных переменных. Это может затруднить интерпретацию. Во многих случаях реальные базовые компоненты могут быть более естественно представлены как разреженные векторы; например, в распознавании лиц компоненты могут естественным образом соответствовать частям лиц.

Разреженные главные компоненты дают более экономное, интерпретируемое представление, чётко подчёркивая, какие из исходных признаков вносят вклад в различия между образцами.

Следующий пример иллюстрирует 16 компонентов, извлеченных с помощью разреженного PCA из набора данных лиц Olivetti. Можно увидеть, как член регуляризации индуцирует много нулей. Кроме того, естественная структура данных приводит к тому, что ненулевые коэффициенты становятся вертикально смежными. Модель не навязывает это математически: каждый компонент — это вектор \(h \in \mathbf{R}^{4096}\), и не существует понятия вертикальной смежности, кроме как при визуализации в удобном для человека виде как изображения 64x64 пикселей. То, что компоненты, показанные ниже, выглядят локальными, является эффектом внутренней структуры данных, которая заставляет такие локальные паттерны минимизировать ошибку реконструкции. Существуют нормы, индуцирующие разреженность, которые учитывают смежность и различные виды структуры; см. [Jen09] для обзора таких методов. Для более подробной информации об использовании Sparse PCA, см. раздел Примеры ниже.

Обратите внимание, что существует множество различных формулировок задачи Sparse PCA. Реализованная здесь основана на [Mrl09] . Оптимизационная задача, которая решается, - это задача PCA (обучение словарю) с \(\ell_1\) штраф на компоненты:

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||V||_{1,1} \\ \text{subject to } & ||U_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{components}\end{split}\]

\(||.||_{\text{Fro}}\) обозначает норму Фробениуса и \(||.||_{1,1}\) обозначает поэлементную матричную норму, которая является суммой абсолютных значений всех элементов матрицы. Индуцирующий разреженность \(||.||_{1,1}\) норма матрицы также предотвращает обучение компонентов от шума, когда доступно мало обучающих образцов. Степень штрафа (и, следовательно, разреженности) может быть скорректирована через гиперпараметр alpha. Малые значения приводят к мягкой регуляризации факторизации, в то время как большие значения сжимают многие коэффициенты до нуля.

Примечание

Хотя в духе онлайн-алгоритма, класс MiniBatchSparsePCA не реализует partial_fit по определению равно

Примеры

• Разложения набора данных Faces

Ссылки

[Mrl09]

«Онлайн-обучение словаря для разреженного кодирования» J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

[Jen09]

“Structured Sparse Principal Component Analysis” R. Jenatton, G. Obozinski, F. Bach, 2009

2.5.2. Ядерный метод главных компонент (kPCA)

2.5.2.1. Точный Kernel PCA

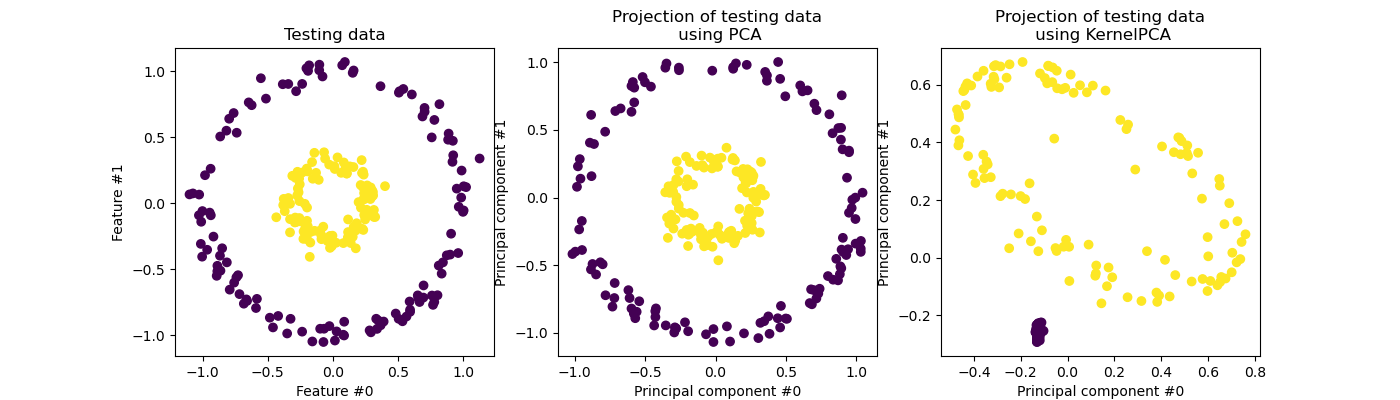
KernelPCA является расширением PCA, которое достигает нелинейного снижения размерности через использование ядер (см. Парные метрики, сходства и ядра) [Scholkopf1997]. Он имеет множество применений, включая шумоподавление, сжатие и структурированное предсказание (оценка зависимости ядра). KernelPCA поддерживает оба transform и inverse_transform.

Примечание

KernelPCA.inverse_transform основывается на ядерном гребне для обучения функции, отображающей выборки из базиса PCA в исходное пространство признаков [Bakir2003]. Таким образом, реконструкция, полученная с KernelPCA.inverse_transform является приближением. Подробнее см. в примере ниже.

Примеры

• Ядерный PCA

• Удаление шума с изображения с использованием ядерного PCA

Ссылки

[Scholkopf1997]

Шёлкхоф, Бернхард, Александр Смола и Клаус-Роберт Мюллер. «Ядерный метод главных компонент». Международная конференция по искусственным нейронным сетям. Springer, Berlin, Heidelberg, 1997.

[Bakir2003]

Bakır, Gökhan H., Jason Weston, and Bernhard Schölkopf. “Learning to find pre-images.” Advances in neural information processing systems 16 (2003): 449-456.

2.5.2.2. Выбор решателя для Kernel PCA

В то время как в PCA количество компонентов ограничено количеством признаков, в KernelPCA количество компонентов ограничено количеством выборок. Многие реальные наборы данных имеют большое количество выборок! В этих случаях поиск все компоненты с полным kPCA — это пустая трата вычислительного времени, так как данные в основном описываются первыми несколькими компонентами (например, n_components<=100). Другими словами, центрированная матрица Грама, которая подвергается разложению по собственным значениям в процессе обучения Kernel PCA, имеет эффективный ранг, значительно меньший её размера. Это ситуация, когда приближённые решатели для собственных значений могут обеспечить ускорение с очень малой потерей точности.

Собственные решатели

Необязательный параметр eigen_solver='randomized' может использоваться для y_indicator уменьшить время вычислений, когда количество запрошенных n_components мало по сравнению с количеством образцов. Он использует рандомизированные методы декомпозиции для нахождения приближенного решения за меньшее время.

Временная сложность рандомизированного KernelPCA является \(O(n_{\mathrm{samples}}^2 \cdot n_{\mathrm{components}})\) вместо \(O(n_{\mathrm{samples}}^3)\) для точного метода, реализованного с eigen_solver='dense'.

Объем памяти рандомизированного KernelPCA также пропорционально \(2 \cdot n_{\mathrm{samples}} \cdot n_{\mathrm{components}}\) вместо \(n_{\mathrm{samples}}^2\) для точного метода.

Примечание: этот метод такой же, как в PCA с использованием рандомизированного SVD.

В дополнение к двум вышеуказанным решателям, eigen_solver='arpack' может использоваться как альтернативный способ получения приближенного разложения. На практике этот метод обеспечивает разумное время выполнения только тогда, когда количество искомых компонентов крайне мало. Он включен по умолчанию, когда желаемое количество компонентов меньше 10 (строго) и количество образцов больше 200 (строго). См. KernelPCA подробности.

Ссылки

• dense solver: документация scipy.linalg.eigh

• randomized solver:

  • Алгоритм 4.3 в “Поиск структуры с помощью случайности: Стохастические алгоритмы для построения приближённых матричных разложений” Halko и др. (2009)

  • “Реализация рандомизированного алгоритма для анализа главных компонент” A. Szlam et al. (2014)

• arpack solver: документация scipy.sparse.linalg.eigsh R. B. Lehoucq, D. C. Sorensen, and C. Yang, (1998)

2.5.3. Усечённое сингулярное разложение и латентно-семантический анализ

TruncatedSVD реализует вариант сингулярного разложения (SVD), который вычисляет только \(k\) наибольшие сингулярные значения, где \(k\) является параметром, задаваемым пользователем.

TruncatedSVD очень похож на PCA, но отличается тем, что матрица \(X\) не требует центрирования. Когда средние значения по столбцам (по признакам) \(X\) вычитаются из значений признаков, усеченное SVD на результирующей матрице эквивалентно PCA.

Об усеченном SVD и латентном семантическом анализе (LSA)

Когда усеченный SVD применяется к матрицам термов-документов (как возвращено CountVectorizer или TfidfVectorizer), это преобразование известно как латентно-семантический анализ (LSA), потому что он преобразует такие матрицы в «семантическое» пространство низкой размерности. В частности, известно, что LSA борется с эффектами синонимии и полисемии (оба означают, что у слова есть несколько значений), что делает матрицы термин-документ слишком разреженными и демонстрирует плохое сходство по таким мерам, как косинусное сходство.

Примечание

LSA также известен как латентное семантическое индексирование, LSI, хотя строго говоря, это относится к его использованию в постоянных индексах для целей информационного поиска.

Математически, усечённое SVD, применённое к обучающим выборкам \(X\) создаёт низкоранговое приближение \(X\):

\[X \approx X_k = U_k \Sigma_k V_k^\top\]

После этой операции, \(U_k \Sigma_k\) является преобразованным обучающим набором с \(k\) признаки (называемые n_components в API).

Чтобы также преобразовать тестовый набор \(X\), мы умножаем его на \(V_k\):

\[X' = X V_k\]

Примечание

В большинстве подходов к LSA в обработке естественного языка (NLP) и информационном поиске (IR) оси матрицы меняются местами \(X\) так, чтобы он имел форму (n_features, n_samples). Мы представляем LSA по-другому, что лучше соответствует API scikit-learn, но найденные сингулярные значения те же.

Хотя TruncatedSVD преобразователь работает с любой матрицей признаков, но его использование на матрицах tf-idf рекомендуется вместо сырых частотных подсчетов в настройках LSA/обработки документов. В частности, сублинейное масштабирование и обратная частота документа должны быть включены (sublinear_tf=True, use_idf=True) чтобы приблизить значения признаков к распределению Гаусса, компенсируя ошибочные предположения LSA о текстовых данных.

Примеры

• Кластеризация текстовых документов с использованием k-means

Ссылки

• Christopher D. Manning, Prabhakar Raghavan и Hinrich Schütze (2008), Introduction to Information Retrieval, Cambridge University Press, глава 18: Матричные разложения и латентно-семантическое индексирование

2.5.4. Словарное обучение

2.5.4.1. Разреженное кодирование с предвычисленным словарём

The SparseCoder объект - это оценщик, который можно использовать для преобразования сигналов в разреженную линейную комбинацию атомов из фиксированного, предварительно вычисленного словаря, такого как дискретный вейвлет-базис. Этот объект, следовательно, не реализует fit метод. Преобразование сводится к задаче разреженного кодирования: поиск представления данных в виде линейной комбинации как можно меньшего количества атомов словаря. Все варианты обучения словаря реализуют следующие методы преобразования, управляемые через transform_method параметр инициализации:

• Ортогональный жадный поиск (Ортогональное согласованное преследование (OMP))

• Регрессия с наименьшим углом (Least Angle Regression)

• Lasso, вычисленный методом наименьшего угла регрессии

• Lasso с использованием координатного спуска (Lasso)

• Пороговая обработка

Пороговая обработка очень быстра, но не дает точных реконструкций. Они показали свою полезность в литературе для задач классификации. Для задач реконструкции изображений ортогональное согласованное преследование дает наиболее точную, несмещенную реконструкцию.

Объекты словарного обучения предлагают, через split_code параметр, возможность разделить положительные и отрицательные значения в результатах разреженного кодирования. Это полезно, когда обучение словаря используется для извлечения признаков, которые будут использоваться для обучения с учителем, потому что это позволяет алгоритму обучения назначать разные веса отрицательным нагрузкам определенного атома, по сравнению с соответствующей положительной нагрузкой.

Код разделения для одного образца имеет длину 2 * n_components и строится по следующему правилу: сначала регулярный код длины n_components вычисляется. Затем первый n_components элементы split_code заполняются положительной частью регулярного кодового вектора. Вторая половина разделенного кода заполняется отрицательной частью кодового вектора, только с положительным знаком. Поэтому split_code неотрицателен.

Примеры

• Разреженное кодирование с предвычисленным словарём

2.5.4.2. Обучение словарю общего вида

Словарное обучение (DictionaryLearning) — это задача матричной факторизации, которая сводится к нахождению (обычно переполненного) словаря, который будет хорошо работать для разреженного кодирования обученных данных.

Представление данных в виде разреженных комбинаций атомов из переполненного словаря считается способом работы первичной зрительной коры млекопитающих. Следовательно, обучение словаря, примененное к патчам изображений, показало хорошие результаты в задачах обработки изображений, таких как восстановление изображений, ретуширование и шумоподавление, а также в задачах контролируемого распознавания.

Обучение словаря — это задача оптимизации, решаемая путем поочередного обновления разреженного кода как решения нескольких задач Lasso при фиксированном словаре, а затем обновления словаря для наилучшего соответствия разреженному коду.

\[\begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2} ||X-UV||_{\text{Fro}}^2+\alpha||U||_{1,1} \\ \text{subject to } & ||V_k||_2 \leq 1 \text{ for all } 0 \leq k < n_{\mathrm{atoms}}\end{split}\]

\(||.||_{\text{Fro}}\) обозначает норму Фробениуса и \(||.||_{1,1}\) обозначает поэлементную матричную норму, которая представляет собой сумму абсолютных значений всех элементов матрицы. После использования такой процедуры для подбора словаря преобразование - это просто шаг разреженного кодирования, который разделяет ту же реализацию со всеми объектами обучения словаря (см. Разреженное кодирование с предвычисленным словарём).

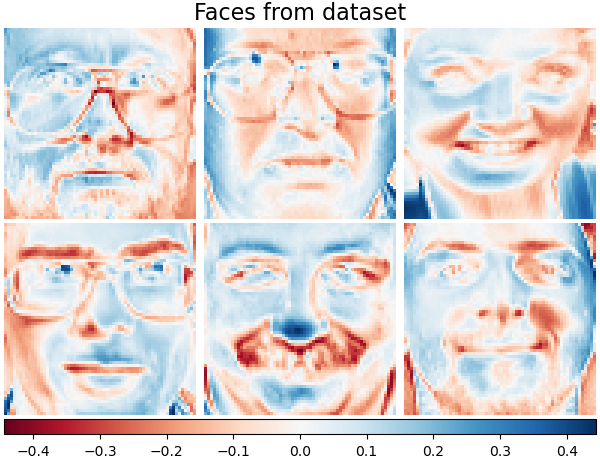
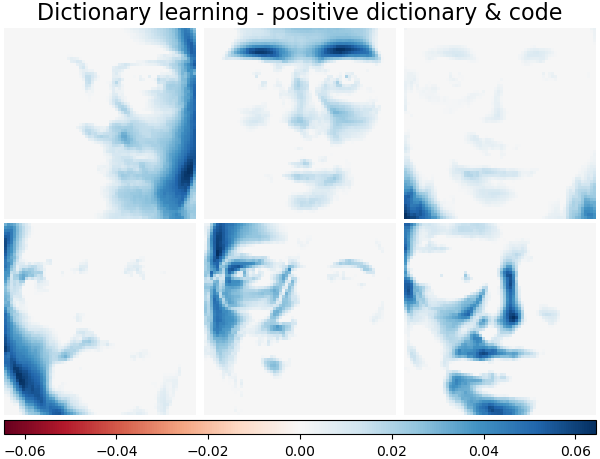
Также возможно ограничить словарь и/или код на положительность, чтобы соответствовать ограничениям, которые могут присутствовать в данных. Ниже приведены лица с применёнными различными ограничениями положительности. Красный указывает на отрицательные значения, синий указывает на положительные значения, а белый представляет нули.

Ссылки

• “Онлайн-обучение словаря для разреженного кодирования” J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009

2.5.4.3. Мини-пакетное обучение словарю

MiniBatchDictionaryLearning реализует более быструю, но менее точную версию алгоритма обучения словаря, которая лучше подходит для больших наборов данных.

По умолчанию, MiniBatchDictionaryLearning разделяет данные на мини-пакеты и оптимизирует в онлайн-режиме, циклически перебирая мини-пакеты заданное количество итераций. Однако в настоящее время не реализует условие остановки.

Оценщик также реализует partial_fit, который обновляет словарь путем итерации только один раз по мини-батчу. Это можно использовать для онлайн-обучения, когда данные не доступны с самого начала, или когда данные не помещаются в память.

Кластеризация для обучения словаря

Обратите внимание, что при использовании словарного обучения для извлечения представления (например, для разреженного кодирования) кластеризация может быть хорошим способом обучения словаря. Например, MiniBatchKMeans оценщик вычислительно эффективен и реализует онлайн-обучение с partial_fit метод.

Пример: Онлайн-обучение словаря частей лиц

Следующее изображение показывает, как выглядит словарь, обученный на патчах изображений 4x4 пикселя, извлеченных из части изображения морды енота.

Примеры

• Удаление шума изображений с использованием обучения словаря

2.5.5. Факторный анализ

В обучении без учителя у нас есть только набор данных \(X = \{x_1, x_2, \dots, x_n \}\). Как этот набор данных можно описать математически? Очень просто continuous latent variable модель для \(X\) является

\[x_i = W h_i + \mu + \epsilon\]

Вектор \(h_i\) называется "латентным", потому что он ненаблюдаем. \(\epsilon\) рассматривается как шумовой член, распределенный по Гауссу со средним 0 и ковариацией \(\Psi\) (т.е. \(\epsilon \sim \mathcal{N}(0, \Psi)\)), \(\mu\) является некоторым произвольным вектором смещения. Такая модель называется "порождающей", так как она описывает, как \(x_i\) генерируется из \(h_i\). Если мы используем все \(x_i\)в виде столбцов для формирования матрицы \(\mathbf{X}\) и все \(h_i\)в качестве столбцов матрицы \(\mathbf{H}\) тогда мы можем записать (с соответствующим образом определенными \(\mathbf{M}\) и \(\mathbf{E}\)):

\[\mathbf{X} = W \mathbf{H} + \mathbf{M} + \mathbf{E}\]

Другими словами, мы разложена матрица \(\mathbf{X}\).

Если \(h_i\) задано, приведенное выше уравнение автоматически подразумевает следующую вероятностную интерпретацию:

\[p(x_i|h_i) = \mathcal{N}(Wh_i + \mu, \Psi)\]

missing_values: int, float, str, np.nan, None или pandas.NA, по умолчанию=np.nan \(h\)Самое простое предположение (основанное на хороших свойствах распределения Гаусса) заключается в том, что \(h \sim \mathcal{N}(0, \mathbf{I})\)В результате получается гауссово распределение как маргинальное распределение \(x\):

\[p(x) = \mathcal{N}(\mu, WW^T + \Psi)\]

Теперь, без каких-либо дополнительных предположений, идея наличия скрытой переменной \(h\) было бы излишним – \(x\) может быть полностью смоделирована с помощью среднего и ковариации. Нам нужно наложить более конкретную структуру на один из этих двух параметров. Простое дополнительное предположение касается структуры ковариации ошибок \(\Psi\):

• \(\Psi = \sigma^2 \mathbf{I}\): Это предположение приводит к вероятностной модели PCA.

• \(\Psi = \mathrm{diag}(\psi_1, \psi_2, \dots, \psi_n)\): Эта модель называется FactorAnalysis, классическая статистическая модель. Матрица W иногда называется "матрицей факторных нагрузок".

Обе модели по сути оценивают гауссово распределение с низкоранговой ковариационной матрицей. Поскольку обе модели вероятностные, они могут быть интегрированы в более сложные модели, например, в смесь факторных анализаторов. Получаются очень разные модели (например, FastICA) если предполагаются негауссовские априорные распределения на скрытых переменных.

Факторный анализ может производить похожие компоненты (столбцы его матрицы загрузки) как PCA. Однако нельзя делать общие утверждения об этих компонентах (например, являются ли они ортогональными):

Основное преимущество факторного анализа перед PCA заключается в том, что он может моделировать дисперсию в каждом направлении входного пространства независимо (гетероскедастичный шум):

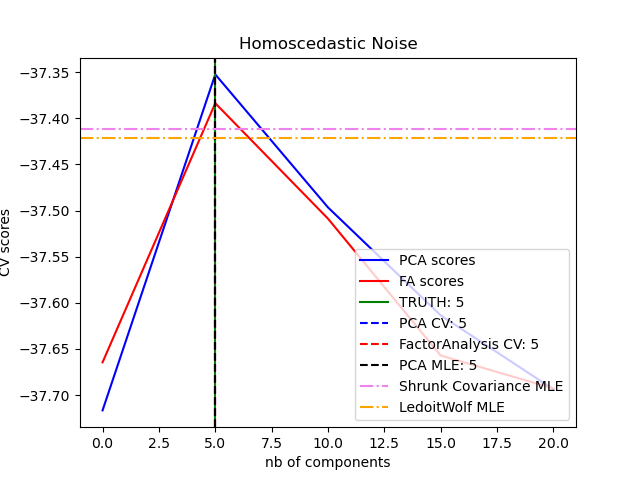
Это позволяет лучше выбирать модель, чем вероятностный PCA в присутствии гетероскедастического шума:

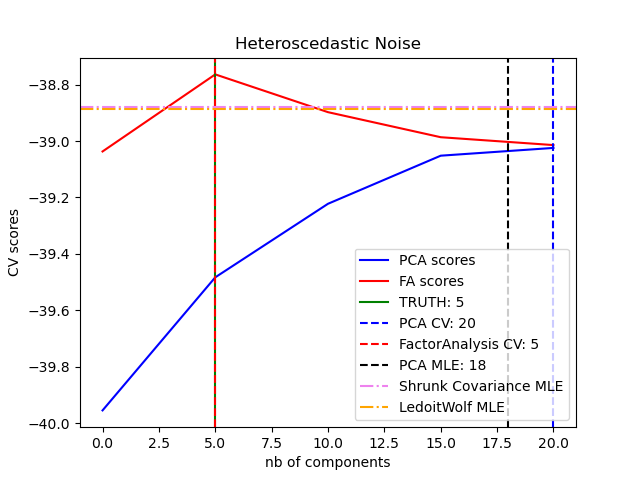
Факторный анализ часто сопровождается вращением факторов (с параметром rotation), обычно для улучшения интерпретируемости. Например, вращение Varimax максимизирует сумму дисперсий квадратов нагрузок, т.е. оно стремится создавать более разреженные факторы, на которые влияют только несколько признаков каждый (“простая структура”). См., например, первый пример ниже.

Примеры

• Факторный анализ (с вращением) для визуализации паттернов

• Выбор модели с вероятностным PCA и факторным анализом (FA)

2.5.6. Анализ независимых компонент (ICA)

Анализ независимых компонент разделяет многомерный сигнал на аддитивные подкомпоненты, которые максимально независимы. Он реализован в scikit-learn с использованием Fast ICA алгоритм. Обычно ICA не используется для уменьшения размерности, а для разделения наложенных сигналов. Поскольку модель ICA не включает член шума, для корректности модели необходимо применять отбеливание. Это можно сделать внутренне с помощью whiten аргумент или вручную с использованием одного из вариантов PCA.

Классически используется для разделения смешанных сигналов (задача, известная как разделение слепых источников), как в примере ниже:

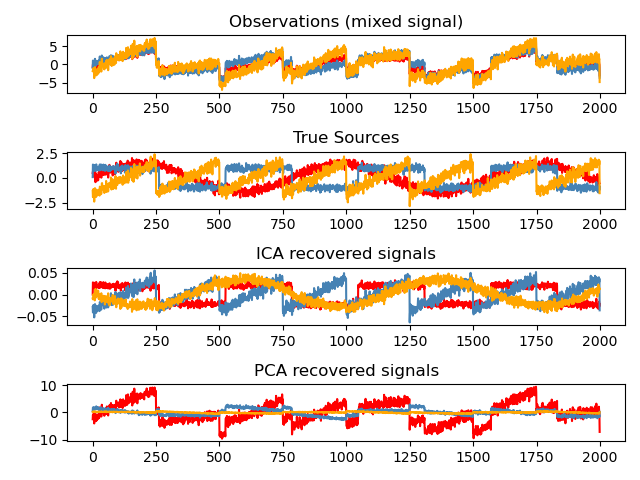
ICA также можно использовать как ещё один нелинейный метод декомпозиции, который находит компоненты с некоторой разреженностью:

Примеры

• Разделение слепых источников с использованием FastICA

• FastICA на 2D облаках точек

• Разложения набора данных Faces

2.5.7. Неотрицательная матричная факторизация (NMF или NNMF)

2.5.7.1. NMF с нормой Фробениуса

NMF [1] является альтернативным подходом к разложению, который предполагает, что данные и компоненты неотрицательны. NMF может быть подключен вместо PCA или его вариантов, в случаях, когда матрица данных не содержит отрицательных значений. Он находит разложение выборок \(X\) в две матрицы \(W\) и \(H\) неотрицательных элементов, оптимизируя расстояние \(d\) между \(X\) и матричное произведение \(WH\). Наиболее широко используемая функция расстояния — это квадрат нормы Фробениуса, которая является очевидным расширением евклидовой нормы на матрицы:

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{\mathrm{Fro}}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

В отличие от PCA, представление вектора получается аддитивным способом, путём наложения компонентов, без вычитания. Такие аддитивные модели эффективны для представления изображений и текста.

Было замечено в [Hoyer, 2004] [2] которые при тщательном ограничении NMF может создавать частичное представление набора данных, что приводит к интерпретируемым моделям. Следующий пример показывает 16 разреженных компонентов, найденных NMF из изображений в наборе данных лиц Olivetti, в сравнении с собственными лицами PCA.

The init атрибут определяет метод инициализации, который применяется и оказывает большое влияние на производительность метода. NMF реализует метод Nonnegative Double Singular Value Decomposition. NNDSVD [4] основан на двух процессах SVD: один аппроксимирует матрицу данных, другой аппроксимирует положительные секции результирующих частичных факторов SVD, используя алгебраическое свойство матриц единичного ранга. Базовый алгоритм NNDSVD лучше подходит для разреженной факторизации. Его варианты NNDSVDa (в котором все нули устанавливаются равными среднему значению всех элементов данных) и NNDSVDar (в котором нули устанавливаются в случайные возмущения, меньшие среднего значения данных, делённого на 100) рекомендуются в плотном случае.

Обратите внимание, что решатель Multiplicative Update ('mu') не может обновлять нули, присутствующие в инициализации, поэтому приводит к худшим результатам при совместном использовании с базовым алгоритмом NNDSVD, который вводит много нулей; в этом случае следует предпочесть NNDSVDa или NNDSVDar.

NMF также может быть инициализирован правильно масштабированными случайными неотрицательными матрицами, установив init="random". Целочисленное семя или RandomState также может быть передано в random_state для контроля воспроизводимости.

В NMF, L1 и L2 априорные распределения могут быть добавлены к функции потерь для регуляризации модели. L2 априор использует норму Фробениуса, а L1 априор использует поэлементную L1 норму. Как в ElasticNet, мы управляем комбинацией L1 и L2 с помощью l1_ratio (\(\rho\)параметр, и интенсивность регуляризации с помощью alpha_W и alpha_H (\(\alpha_W\) и \(\alpha_H\)) параметры. Априорные вероятности масштабируются количеством образцов (\(n\_samples\)) для H и количество признаков (\(n\_features\)) для W чтобы сбалансировать их влияние относительно друг друга и члена соответствия данным, насколько возможно независимо от размера обучающей выборки. Затем члены априорных распределений:

\[(\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

и регуляризованная целевая функция:

\[d_{\mathrm{Fro}}(X, WH) + (\alpha_W \rho ||W||_1 + \frac{\alpha_W(1-\rho)}{2} ||W||_{\mathrm{Fro}} ^ 2) * n\_features + (\alpha_H \rho ||H||_1 + \frac{\alpha_H(1-\rho)}{2} ||H||_{\mathrm{Fro}} ^ 2) * n\_samples\]

2.5.7.2. NMF с бета-дивергенцией

Как описано ранее, наиболее широко используемая функция расстояния - это квадрат нормы Фробениуса, которая является очевидным расширением евклидовой нормы на матрицы:

\[d_{\mathrm{Fro}}(X, Y) = \frac{1}{2} ||X - Y||_{Fro}^2 = \frac{1}{2} \sum_{i,j} (X_{ij} - {Y}_{ij})^2\]

Другие функции расстояния могут использоваться в NMF, например, (обобщенная) дивергенция Кульбака-Лейблера (KL), также называемая I-дивергенцией:

\[d_{KL}(X, Y) = \sum_{i,j} (X_{ij} \log(\frac{X_{ij}}{Y_{ij}}) - X_{ij} + Y_{ij})\]

Или дивергенция Итакуры-Сайто (IS):

\[d_{IS}(X, Y) = \sum_{i,j} (\frac{X_{ij}}{Y_{ij}} - \log(\frac{X_{ij}}{Y_{ij}}) - 1)\]

Эти три расстояния являются частными случаями семейства бета-расхождений, с \(\beta = 2, 1, 0\) соответственно [6]. Бета-дивергенция определяется как:

\[d_{\beta}(X, Y) = \sum_{i,j} \frac{1}{\beta(\beta - 1)}(X_{ij}^\beta + (\beta-1)Y_{ij}^\beta - \beta X_{ij} Y_{ij}^{\beta - 1})\]

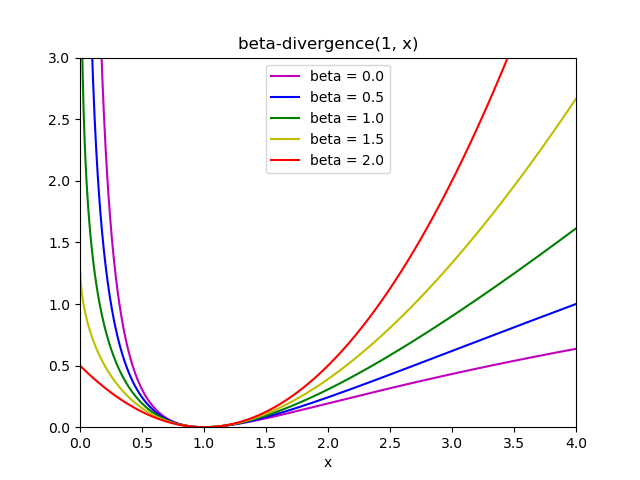
Обратите внимание, что это определение недействительно, если \(\beta \in (0; 1)\), однако она может быть непрерывно расширена до определений \(d_{KL}\) и \(d_{IS}\) соответственно.

Реализованные решатели NMF

NMF реализует два решателя, используя координатный спуск ('cd') [5], и Мультипликативное обновление (‘mu’) [6]. Решатель 'mu' может оптимизировать любую бета-дивергенцию, включая, конечно, норму Фробениуса (\(\beta=2\)), (обобщенная) дивергенция Кульбака-Лейблера (\(\beta=1\)) и расхождение Итакуры-Сайто (\(\beta=0\)). Обратите внимание, что для \(\beta \in (1; 2)\), решатель 'mu' значительно быстрее, чем для других значений \(\beta\). Также обратите внимание, что с отрицательным (или 0, т.е. ‘itakura-saito’) \(\beta\), входная матрица не может содержать нулевые значения.

Решатель 'cd' может оптимизировать только норму Фробениуса. Из-за присущей NMF невыпуклости, различные решатели могут сходиться к различным минимумам, даже при оптимизации той же функции расстояния.

NMF лучше всего использовать с fit_transform метод, который возвращает матрицу W. Матрица H сохраняется в обученной модели в components_ атрибут; метод transform разложит новую матрицу X_new на основе этих сохраненных компонентов:

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)

Примеры

• Разложения набора данных Faces

• Извлечение тем с использованием неотрицательной матричной факторизации и латентного размещения Дирихле

2.5.7.3. Мини-пакетное неотрицательное матричное разложение

MiniBatchNMF [7] реализует более быструю, но менее точную версию неотрицательного матричного разложения (т.е. NMF), лучше подходит для больших наборов данных.

По умолчанию, MiniBatchNMF разделяет данные на мини-пакеты и оптимизирует модель NMF в онлайн-режиме, циклически перебирая мини-пакеты указанное количество итераций. Параметр batch_size параметр управляет размером батчей.

Для ускорения алгоритма мини-пакетов также можно масштабировать прошлые пакеты, придавая им меньшее значение, чем новым пакетам. Это делается путем введения так называемого фактора забывания, управляемого forget_factor параметр.

Оценщик также реализует partial_fit, который обновляет H путем итерации только один раз по мини-батчу. Это может использоваться для онлайн-обучения, когда данные не доступны с самого начала или когда данные не помещаются в память.

Ссылки

[1]

«Изучение частей объектов с помощью неотрицательного матричного разложения» D. Lee, S. Seung, 1999

[2]

“Неотрицательное матричное разложение с ограничениями разреженности” P. Hoyer, 2004

[4]

"Инициализация на основе SVD: Хороший старт для неотрицательного матричного разложения" C. Boutsidis, E. Gallopoulos, 2008

[5]

“Быстрые локальные алгоритмы для крупномасштабного неотрицательного матричного и тензорного разложения.” A. Cichocki, A. Phan, 2009

[6] (1,2)

“Алгоритмы для неотрицательного матричного разложения с бета-дивергенцией” C. Fevotte, J. Idier, 2011

[7]

«Онлайн-алгоритмы для неотрицательного матричного разложения с дивергенцией Итакуры-Сайто» А. Лефевр, Ф. Бах, К. Февот, 2011

2.5.8. Латентное размещение Дирихле (LDA)

Латентное размещение Дирихле — это генеративная вероятностная модель для коллекций дискретных наборов данных, таких как текстовые корпуса. Это также тематическая модель, используемая для обнаружения абстрактных тем из коллекции документов.

Графическая модель LDA — это трёхуровневая генеративная модель:

Примечание к обозначениям, представленным в графической модели выше, которые можно найти в Hoffman et al. (2013):

• Корпус — это коллекция \(D\) документов.

• Документ \(d \in D\) является последовательностью \(N_d\) слова.

• Существуют \(K\) темы в корпусе.

• Коробки представляют повторную выборку.

В графической модели каждый узел является случайной величиной и играет роль в генеративном процессе. Закрашенный узел указывает на наблюдаемую переменную, а незакрашенный — на скрытую (латентную) переменную. В данном случае слова в корпусе — это единственные данные, которые мы наблюдаем. Латентные переменные определяют случайную смесь тем в корпусе и распределение слов в документах. Цель LDA — использовать наблюдаемые слова для вывода скрытой тематической структуры.

Подробности о моделировании текстовых корпусов

При моделировании текстовых корпусов модель предполагает следующий генеративный процесс для корпуса с \(D\) документы и \(K\) темы, с \(K\) соответствующий n_components в API:

1. Для каждой темы \(k \in K\), рисовать \(\beta_k \sim \mathrm{Dirichlet}(\eta)\). Это обеспечивает распределение по словам, т.е. вероятность появления слова в теме \(k\). \(\eta\) соответствует topic_word_prior.

2. Для каждого документа \(d \in D\), нарисуйте пропорции тем \(\theta_d \sim \mathrm{Dirichlet}(\alpha)\). \(\alpha\) соответствует doc_topic_prior.

3. Для каждого слова \(n=1,\cdots,N_d\) в документе \(d\):

   1. Нарисовать назначение темы \(z_{dn} \sim \mathrm{Multinomial} (\theta_d)\)

   2. Нарисуйте наблюдаемое слово \(w_{dn} \sim \mathrm{Multinomial} (\beta_{z_{dn}})\)

Для оценки параметров апостериорное распределение:

\[p(z, \theta, \beta |w, \alpha, \eta) = \frac{p(z, \theta, \beta|\alpha, \eta)}{p(w|\alpha, \eta)}\]

Поскольку апостериорное распределение невычислимо, вариационный байесовский метод использует более простое распределение \(q(z,\theta,\beta | \lambda, \phi, \gamma)\) для его аппроксимации, и эти вариационные параметры \(\lambda\), \(\phi\), \(\gamma\) оптимизированы для максимизации нижней границы доказательства (ELBO):

\[\log\: P(w | \alpha, \eta) \geq L(w,\phi,\gamma,\lambda) \overset{\triangle}{=} E_{q}[\log\:p(w,z,\theta,\beta|\alpha,\eta)] - E_{q}[\log\:q(z, \theta, \beta)]\]

Максимизация ELBO эквивалентна минимизации дивергенции Кульбака-Лейблера (KL) между \(q(z,\theta,\beta)\) и истинное апостериорное распределение \(p(z, \theta, \beta |w, \alpha, \eta)\).

LatentDirichletAllocation реализует онлайн-алгоритм вариационного Байеса и поддерживает как онлайн, так и пакетные методы обновления. В то время как пакетный метод обновляет вариационные переменные после каждого полного прохода по данным, онлайн-метод обновляет вариационные переменные на основе мини-пакетов точек данных.

Примечание

Хотя онлайн-метод гарантированно сходится к локальному оптимуму, качество этого оптимума и скорость сходимости могут зависеть от размера мини-пакета и атрибутов, связанных с настройкой скорости обучения.

Когда LatentDirichletAllocation применяется к матрице 'документ-термин', матрица будет разложена на матрицу 'тема-термин' и матрицу 'документ-тема'. При этом матрица 'тема-термин' хранится как components_ в модели, матрица "документ-тема" может быть вычислена из transform метод.

LatentDirichletAllocation также реализует partial_fit метод. Используется, когда данные могут быть получены последовательно.

Примеры

• Извлечение тем с использованием неотрицательной матричной факторизации и латентного размещения Дирихле

Ссылки

• “Latent Dirichlet Allocation” Д. Блей, А. Нг, М. Джордан, 2003

• «Онлайн-обучение для латентного размещения Дирихле» М. Хоффман, Д. Блей, Ф. Бах, 2010

• «Стохастический вариационный вывод» M. Hoffman, D. Blei, C. Wang, J. Paisley, 2013

• “Критерий варимакс для аналитического вращения в факторном анализе” H. F. Kaiser, 1958

Смотрите также Снижение размерности для снижения размерности с помощью анализа компонентов соседства.