2.3. Кластеризация

Кластеризация неразмеченных данных может быть выполнено с помощью модуля sklearn.cluster.

Каждый алгоритм кластеризации представлен в двух вариантах: класс, который реализует fit метод для изучения кластеров на обучающих данных и функцию, которая, учитывая обучающие данные, возвращает массив целочисленных меток, соответствующих различным кластерам. Для класса метки по обучающим данным можно найти в labels_ атрибут.

Входные данные

Важно отметить, что алгоритмы, реализованные в этом модуле, могут принимать различные типы матриц на вход. Все методы принимают стандартные матрицы данных формы (n_samples, n_features). Их можно получить из классов в sklearn.feature_extraction модуль. Для AffinityPropagation, SpectralClustering и DBSCAN также можно вводить матрицы сходства формы (n_samples, n_samples). Их можно получить из функций в sklearn.metrics.pairwise модуль.

2.3.1. Обзор методов кластеризации

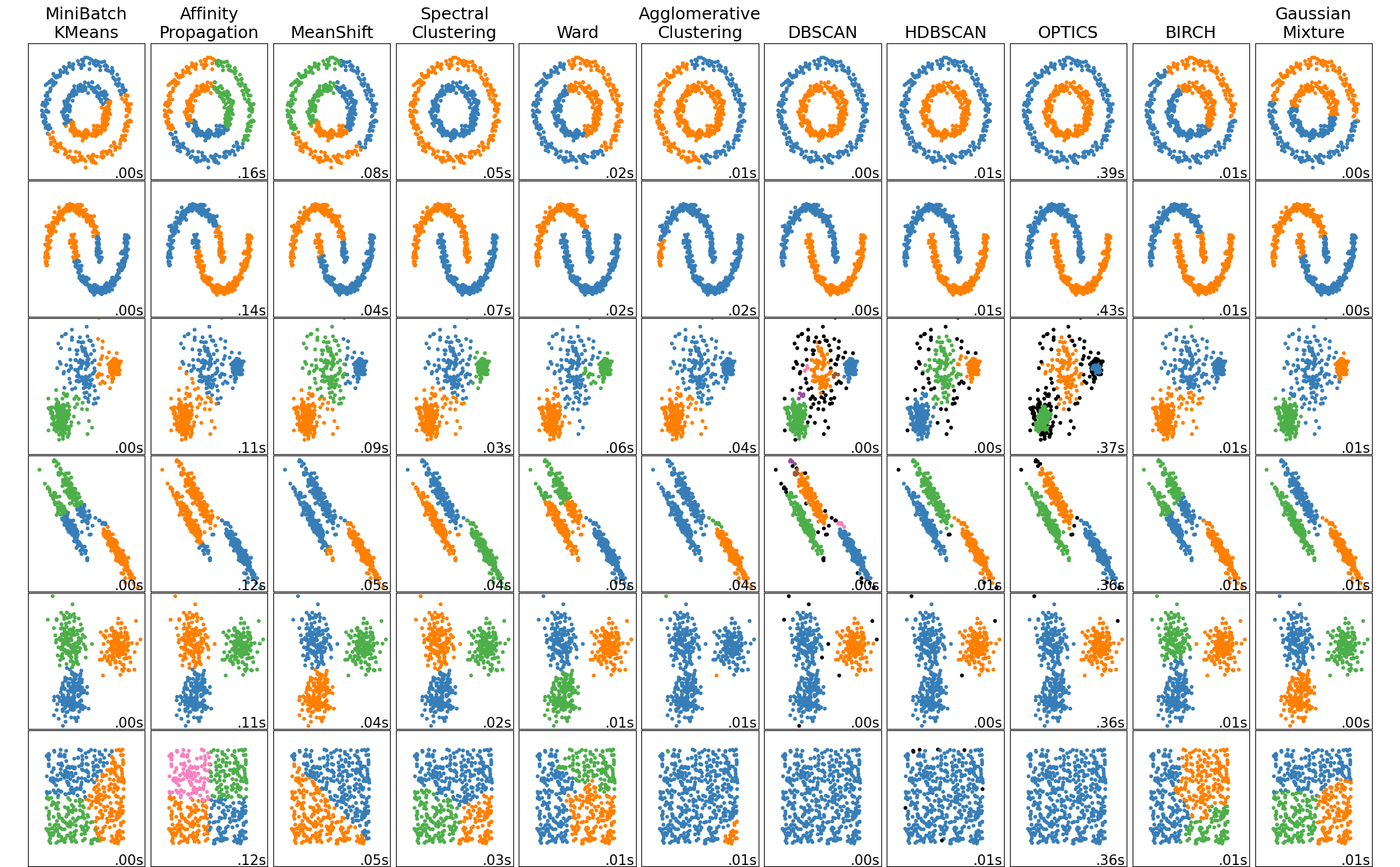
Сравнение алгоритмов кластеризации в scikit-learn

Имя метода	Параметры	Масштабируемость	Случай использования	Геометрия (используемая метрика)
K-Means	количество кластеров	Очень большие n_samples, medium n_clusters с Код MiniBatch	Универсальный, равный размер кластеров, плоская геометрия, не слишком много кластеров, индуктивный	Расстояния между точками
Распространение аффинности	демпфирование, предпочтение образца	Не масштабируется с n_samples	Много кластеров, неравномерный размер кластеров, неевклидова геометрия, индуктивный	Графовое расстояние (например, граф ближайших соседей)
Mean-shift	bandwidth	Не масштабируется с n_samples	Много кластеров, неравномерный размер кластеров, неевклидова геометрия, индуктивный	Расстояния между точками
Спектральная кластеризация	количество кластеров	Средний n_samples, малый n_clusters	Мало кластеров, равный размер кластеров, не плоская геометрия, транзитивное обучение	Графовое расстояние (например, граф ближайших соседей)
Иерархическая кластеризация Уорда	количество кластеров или порог расстояния	Большой n_samples и n_clusters	Много кластеров, возможно, ограничения связности, транзитивное обучение	Расстояния между точками
Агломеративная кластеризация	количество кластеров или порог расстояния, тип связи, расстояние	Большой n_samples и n_clusters	Много кластеров, возможно ограничения связности, неевклидовы расстояния, транзитивные	Любое попарное расстояние
DBSCAN	размер окрестности	Очень большие n_samples, medium n_clusters	Неплоская геометрия, неравные размеры кластеров, удаление выбросов, транзитивность	Расстояния между ближайшими точками
HDBSCAN	минимальное членство в кластере, минимальное количество соседей точки	большой n_samples, medium n_clusters	Неевклидова геометрия, неравные размеры кластеров, удаление выбросов, транзитивное, иерархическое, переменная плотность кластеров	Расстояния между ближайшими точками
OPTICS	минимальное членство в кластере	Очень большие n_samples, большие n_clusters	Неевклидова геометрия, неравные размеры кластеров, переменная плотность кластеров, удаление выбросов, транзитивность	Расстояния между точками
Гауссовские смеси	много	Не масштабируется	Плоская геометрия, хороша для оценки плотности, индуктивная	Расстояния Махаланобиса до центров
BIRCH	коэффициент ветвления, порог, опциональный глобальный кластеризатор.	Большой n_clusters и n_samples	Большой набор данных, удаление выбросов, сокращение данных, индуктивный	Евклидово расстояние между точками
Биссекционный K-Means	количество кластеров	Очень большие n_samples, medium n_clusters	Универсальный, равный размер кластеров, плоская геометрия, нет пустых кластеров, индуктивный, иерархический	Расстояния между точками

Кластеризация с неевклидовой геометрией полезна, когда кластеры имеют специфическую форму, т.е. неевклидово многообразие, и стандартное евклидово расстояние не является подходящей метрикой. Этот случай показан в двух верхних строках рисунка выше.

Гауссовские смеси, полезные для кластеризации, описаны в другой раздел документации посвященный моделям смеси. KMeans можно рассматривать как частный случай гауссовской модели смеси с равной ковариацией на компонент.

Трансдуктивный методы кластеризации (в отличие от индуктивный методы кластеризации) не предназначены для применения к новым, невидимым данным.

Примеры

• Индуктивная кластеризация: Пример индуктивной модели кластеризации для обработки новых данных.

2.3.2. K-means

The KMeans алгоритм кластеризует данные, пытаясь разделить образцы на n групп с равной дисперсией, минимизируя критерий, известный как инерция или внутрикластерная сумма квадратов (см. ниже). Этот алгоритм требует указания количества кластеров. Он хорошо масштабируется на большое количество образцов и использовался в широком диапазоне областей применения во многих различных областях.

Алгоритм k-средних делит набор \(N\) образцы \(X\) в \(K\) непересекающиеся кластеры \(C\), каждый из которых описывается средним значением \(\mu_j\) ‘newton-cholesky’ \(X\), хотя они находятся в одном пространстве.

Алгоритм K-средних стремится выбрать центроиды, которые минимизируют инерция, или критерий суммы квадратов внутри кластера:

\[\sum_{i=0}^{n}\min_{\mu_j \in C}(||x_i - \mu_j||^2)\]

Инерцию можно рассматривать как меру внутренней согласованности кластеров. Она страдает от различных недостатков:

• Инерция предполагает, что кластеры выпуклые и изотропные, что не всегда верно. Она плохо реагирует на вытянутые кластеры или многообразия неправильной формы.

• Инерция не является нормализованной метрикой: мы просто знаем, что меньшие значения лучше, а ноль оптимален. Но в очень многомерных пространствах евклидовы расстояния имеют тенденцию увеличиваться (это пример так называемого "проклятия размерности"). Запуск алгоритма уменьшения размерности, такого как Метод главных компонент (PCA) перед кластеризацией k-средних может смягчить эту проблему и ускорить вычисления.

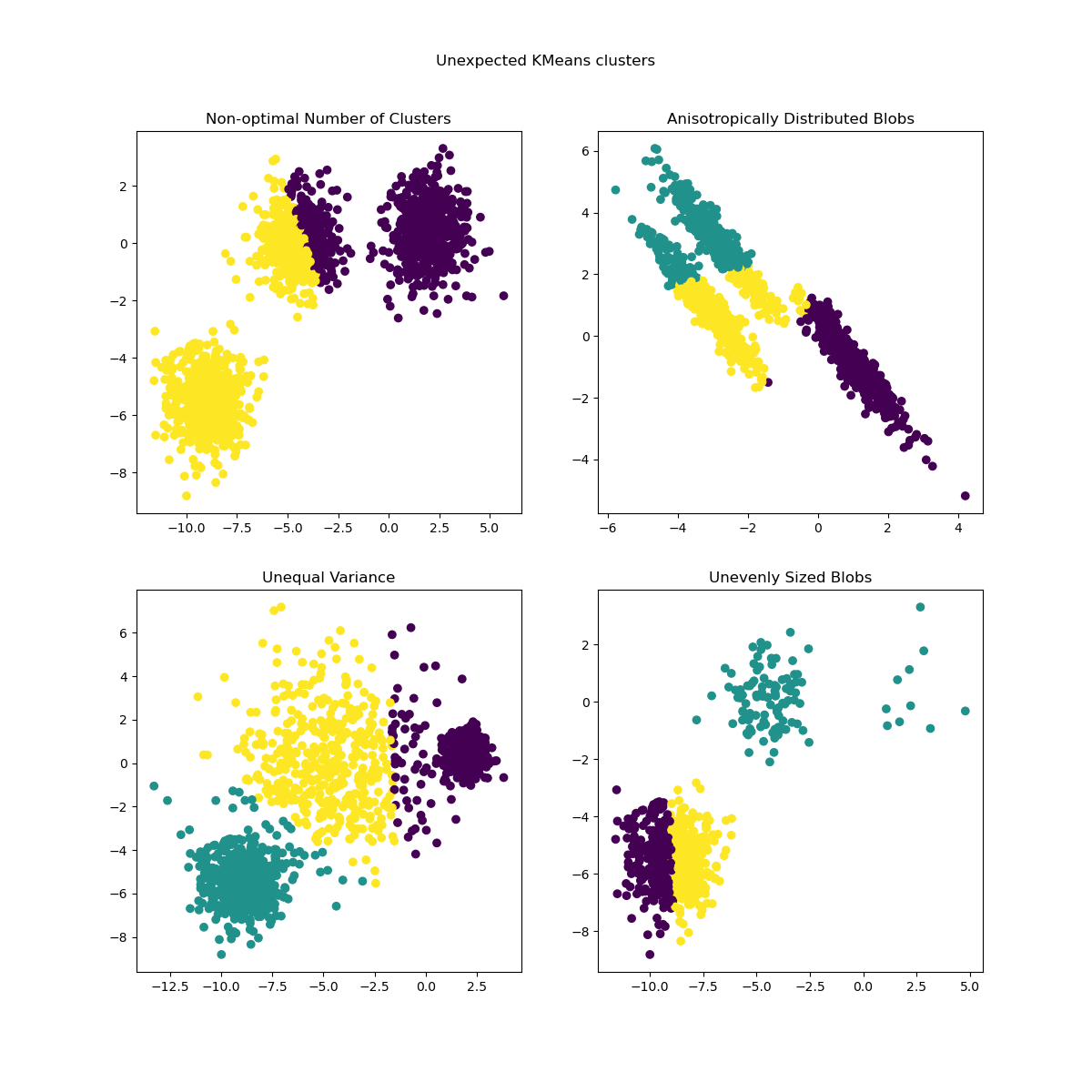
Для более подробных описаний показанных выше проблем и способов их решения обратитесь к примерам Демонстрация предположений k-means и Выбор количества кластеров с помощью анализа силуэта для кластеризации KMeans.

K-means часто называют алгоритмом Ллойда. В общих чертах алгоритм состоит из трех шагов. Первый шаг выбирает начальные центроиды, причем самый базовый метод — выбрать \(k\) выборки из набора данных \(X\). После инициализации K-средних состоит из цикла между двумя другими шагами. Первый шаг назначает каждый образец его ближайшему центроиду. Второй шаг создает новые центроиды, беря среднее значение всех образцов, назначенных каждому предыдущему центроиду. Разница между старыми и новыми центроидами вычисляется, и алгоритм повторяет эти последние два шага, пока это значение не станет меньше порога. Другими словами, он повторяется, пока центроиды не перестанут значительно двигаться.

K-means эквивалентен алгоритму максимизации ожидания с небольшой, одинаковой, диагональной ковариационной матрицей.

Алгоритм также можно понять через концепцию Диаграммы Вороного. Сначала вычисляется диаграмма Вороного точек с использованием текущих центроидов. Каждый сегмент в диаграмме Вороного становится отдельным кластером. Во-вторых, центроиды обновляются до среднего каждого сегмента. Алгоритм затем повторяет это, пока не выполнится критерий остановки. Обычно алгоритм останавливается, когда относительное уменьшение целевой функции между итерациями меньше заданного значения допуска. Это не так в этой реализации: итерация останавливается, когда центроиды перемещаются меньше, чем допуск.

При достаточном времени K-средние всегда сойдутся, однако это может быть к локальному минимуму. Это сильно зависит от инициализации центроидов. В результате вычисление часто выполняется несколько раз с разными инициализациями центроидов. Один метод, помогающий решить эту проблему, — схема инициализации k-means++, которая реализована в scikit-learn (используйте init='k-means++' параметр). Это инициализирует центроиды так, чтобы они были (обычно) удалены друг от друга, что приводит, вероятно, к лучшим результатам, чем случайная инициализация, как показано в ссылке. Подробные примеры сравнения различных схем инициализации см. 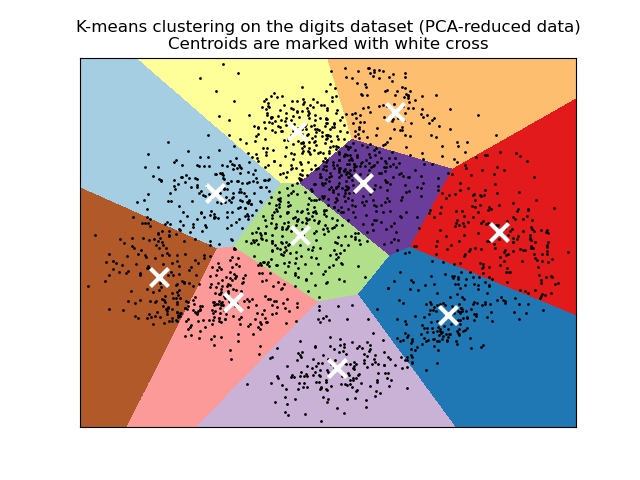в Демонстрация кластеризации K-Means на данных рукописных цифр и Эмпирическая оценка влияния инициализации k-means.

K-means++ также может быть вызван независимо для выбора начальных точек для других алгоритмов кластеризации, см. sklearn.cluster.kmeans_plusplus для подробностей и примеров использования.

Алгоритм поддерживает веса образцов, которые могут быть заданы параметром sample_weight. Это позволяет назначать больший вес некоторым образцам при вычислении центров кластеров и значений инерции. Например, назначение веса 2 образцу эквивалентно добавлению дубликата этого образца в набор данных \(X\).

Примеры

• Кластеризация текстовых документов с использованием k-means: Кластеризация документов с использованием KMeans и MiniBatchKMeans на основе разреженных данных

• Пример инициализации K-Means++: Использование K-means++ для выбора начальных точек для других алгоритмов кластеризации.

2.3.2.1. Низкоуровневый параллелизм

KMeans использует преимущества параллелизма на основе OpenMP через Cython. Небольшие блоки данных (256 образцов) обрабатываются параллельно, что также обеспечивает низкое потребление памяти. Для получения дополнительной информации о том, как управлять количеством потоков, обратитесь к нашей Параллелизм примечания.

Примеры

• Демонстрация предположений k-means: Демонстрация случаев, когда k-средних работает интуитивно и когда нет

• Демонстрация кластеризации K-Means на данных рукописных цифр: Кластеризация рукописных цифр

Ссылки

• “k-means++: Преимущества тщательной инициализации” Артур, Дэвид и Сергей Васильвицкий, Труды восемнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, Общество промышленной и прикладной математики (2007)

2.3.2.2. Mini Batch K-Means

The MiniBatchKMeans является вариантом KMeans алгоритм, который использует мини-пакеты для сокращения времени вычислений, при этом все еще пытаясь оптимизировать ту же целевую функцию. Мини-пакеты — это подмножества входных данных, случайно выбираемые на каждой итерации обучения. Эти мини-пакеты значительно сокращают объем вычислений, необходимых для сходимости к локальному решению. В отличие от других алгоритмов, сокращающих время сходимости k-средних, мини-пакетный k-средних дает результаты, которые обычно лишь немного хуже, чем у стандартного алгоритма.

Алгоритм итерирует между двумя основными шагами, аналогично классическому k-means. На первом шаге, \(b\) образцы случайным образом выбираются из набора данных, чтобы сформировать мини-пакет. Затем они присваиваются ближайшему центроиду. На втором шаге центроиды обновляются. В отличие от k-средних, это делается на основе каждого образца. Для каждого образца в мини-пакете присвоенный центроид обновляется путём взятия скользящего среднего образца и всех предыдущих образцов, присвоенных этому центроиду. Это приводит к уменьшению скорости изменения центроида со временем. Эти шаги выполняются до сходимости или достижения предопределённого количества итераций.

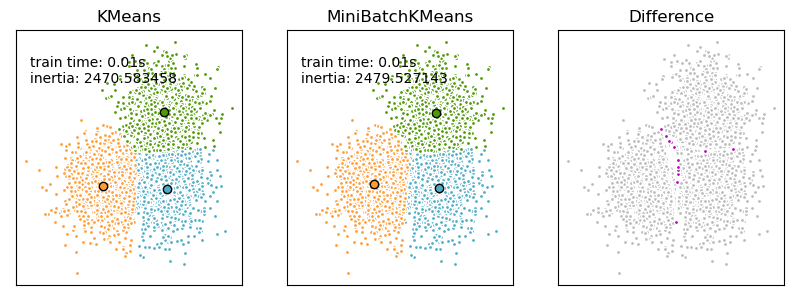
MiniBatchKMeans сходится быстрее, чем KMeans, но качество результатов снижается. На практике эта разница в качестве может быть довольно небольшой, как показано в примере и цитируемой ссылке.

Примеры

• Сравнение алгоритмов кластеризации K-Means и MiniBatchKMeans: Сравнение KMeans и MiniBatchKMeans

• Кластеризация текстовых документов с использованием k-means: Кластеризация документов с использованием KMeans и MiniBatchKMeans на основе разреженных данных

• Онлайн-обучение словаря частей лиц

Ссылки

• “Web Scale K-Means clustering” D. Sculley, Труды 19-й международной конференции по всемирной паутине (2010).

2.3.3. Affinity Propagation

AffinityPropagation создает кластеры, отправляя сообщения между парами образцов до сходимости. Набор данных затем описывается с использованием небольшого числа экземпляров, которые идентифицируются как наиболее репрезентативные для других образцов. Сообщения, отправляемые между парами, представляют пригодность одного образца быть экземпляром другого, что обновляется в ответ на значения от других пар. Это обновление происходит итеративно до сходимости, после чего выбираются окончательные экземпляры и, следовательно, дается окончательная кластеризация.

Распространение сходства может быть интересным, поскольку оно выбирает количество кластеров на основе предоставленных данных. Для этой цели два важных параметра — это предпочтение, который контролирует, сколько экземпляров используется, и коэффициент демпфирования которая демпфирует сообщения ответственности и доступности, чтобы избежать числовых колебаний при обновлении этих сообщений.

Основной недостаток Affinity Propagation — его сложность. Алгоритм имеет временную сложность порядка \(O(N^2 T)\), где \(N\) — это количество образцов и \(T\) это количество итераций до сходимости. Кроме того, сложность по памяти имеет порядок \(O(N^2)\) если используется плотная матрица сходства, но приводима, если используется разреженная матрица сходства. Это делает распространение аффинности наиболее подходящим для наборов данных малого и среднего размера.

Описание алгоритма

Сообщения, отправляемые между точками, принадлежат к одной из двух категорий. Первая — ответственность \(r(i, k)\), что является накопленным свидетельством того, что выборка \(k\) должен быть экземпляром для образца \(i\). Второй - это доступность \(a(i, k)\) что представляет собой накопленные доказательства того, что образец \(i\) должен выбрать образец \(k\) быть его экземпляром, и рассматривает значения для всех других образцов, которые \(k\) должен быть экземпляром. Таким образом, экземпляры выбираются образцами, если они (1) достаточно похожи на многие образцы и (2) выбраны многими образцами в качестве представителей самих себя.

Более формально, ответственность образца \(k\) быть экземпляром для выборки \(i\) задается формулой:

\[r(i, k) \leftarrow s(i, k) - max [ a(i, k') + s(i, k') \forall k' \neq k ]\]

Где \(s(i, k)\) это сходство между образцами \(i\) и \(k\). The availability of sample \(k\) быть экземпляром образца \(i\) задается формулой:

\[a(i, k) \leftarrow min [0, r(k, k) + \sum_{i'~s.t.~i' \notin \{i, k\}}{r(i', k)}]\]

Для начала все значения для \(r\) и \(a\) устанавливаются в ноль, и вычисление каждой итерации продолжается до сходимости. Как обсуждалось выше, чтобы избежать числовых колебаний при обновлении сообщений, коэффициент демпфирования \(\lambda\) вводится в итерационный процесс:

\[r_{t+1}(i, k) = \lambda\cdot r_{t}(i, k) + (1-\lambda)\cdot r_{t+1}(i, k)\]

\[a_{t+1}(i, k) = \lambda\cdot a_{t}(i, k) + (1-\lambda)\cdot a_{t+1}(i, k)\]

где \(t\) указывает количество итераций.

Примеры

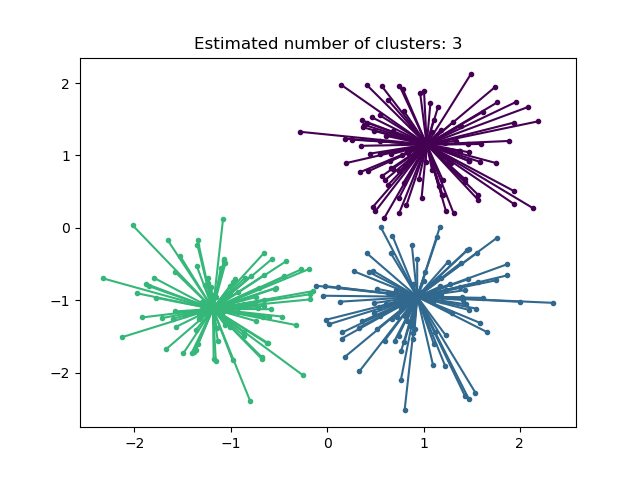
• Демонстрация алгоритма кластеризации с распространением аффинности: Распространение сходства на синтетических 2D-наборах данных с 3 классами

• Визуализация структуры фондового рынка Распространение сходства на финансовых временных рядах для поиска групп компаний

2.3.4. Mean Shift

MeanShift кластеризация направлена на обнаружение blobs в плавной плотности выборок. Это алгоритм на основе центроидов, который работает путем обновления кандидатов для центроидов как среднего точек в заданной области. Затем эти кандидаты фильтруются на этапе постобработки для устранения почти дубликатов и формирования окончательного набора центроидов.

Математические детали

Положение кандидатов в центроиды итеративно корректируется с использованием техники, называемой hill climbing, которая находит локальные максимумы оцененной плотности вероятности. Для заданного кандидата в центроид \(x\) для итерации \(t\), кандидат обновляется согласно следующему уравнению:

\[x^{t+1} = x^t + m(x^t)\]

Где \(m\) является средний сдвиг вектор, который вычисляется для каждого центроида и указывает в сторону области максимального увеличения плотности точек. Для вычисления \(m\) мы определяем \(N(x)\) как окрестность образцов в пределах заданного расстояния вокруг \(x\). Затем \(m\) вычисляется с использованием следующего уравнения, эффективно обновляя центроид до среднего значения выборок в его окрестности:

\[m(x) = \frac{1}{|N(x)|} \sum_{x_j \in N(x)}x_j - x\]

В общем случае, уравнение для \(m\) зависит от ядра, используемого для оценки плотности. Общая формула:

\[m(x) = \frac{\sum_{x_j \in N(x)}K(x_j - x)x_j}{\sum_{x_j \in N(x)}K(x_j - x)} - x\]

В нашей реализации, \(K(x)\) равно 1, если \(x\) достаточно мал и равен 0 в противном случае. По сути \(K(y - x)\) указывает, является ли \(y\) находится в окрестности \(x\).

Алгоритм автоматически устанавливает количество кластеров вместо того, чтобы полагаться на параметр bandwidth, который определяет размер области для поиска. Этот параметр может быть установлен вручную, но может быть оценён с использованием предоставленного estimate_bandwidth функция, которая вызывается, если полоса пропускания не задана.

Алгоритм не является высокомасштабируемым, так как требует нескольких поисков ближайших соседей во время выполнения алгоритма. Алгоритм гарантированно сходится, однако итерации прекратятся, когда изменение центроидов станет малым.

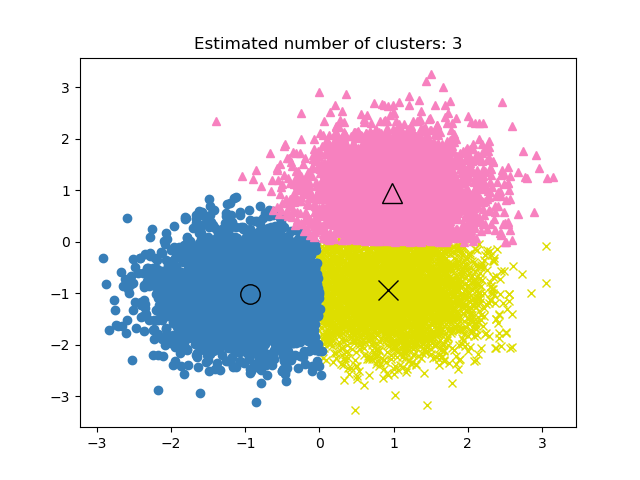
Маркировка нового образца выполняется путем нахождения ближайшего центроида для заданного образца.

Примеры

• Демонстрация алгоритма кластеризации mean-shiftСписок 2D массивов, соответствующих каждой многоклассовой решающей функции.

Ссылки

• “Mean shift: A robust approach toward feature space analysis” D. Comaniciu и P. Meer, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)

2.3.5. Спектральная кластеризация

SpectralClustering выполняет низкоразмерное вложение матрицы сходства между образцами, за которым следует кластеризация, например, с помощью KMeans, компонентов собственных векторов в низкоразмерном пространстве. Это особенно вычислительно эффективно, если матрица сходства разреженная и amg решатель используется для проблемы собственных значений (Примечание, что amg solver требует, чтобы pyamg модуль установлен.)

Текущая версия SpectralClustering требует указания количества кластеров заранее. Она хорошо работает для небольшого числа кластеров, но не рекомендуется для многих кластеров.

Для двух кластеров SpectralClustering решает выпуклую релаксацию нормализованные разрезы задачу на графе сходства: разделение графа на две части так, чтобы вес разрезанных ребер был мал по сравнению с весами ребер внутри каждого кластера. Этот критерий особенно интересен при работе с изображениями, где вершины графа — пиксели, а веса ребер графа сходства вычисляются с использованием функции градиента изображения.

Предупреждение

Преобразование расстояния в хорошо обусловленные сходства

Обратите внимание, что если значения вашей матрицы сходства распределены неравномерно, например, содержат отрицательные значения или представляют собой матрицу расстояний, а не сходства, спектральная задача будет сингулярной и неразрешимой. В этом случае рекомендуется применить преобразование к элементам матрицы. Например, в случае знаковой матрицы расстояний обычно применяется тепловое ядро:

similarity = np.exp(-beta * distance / distance.std())

См. примеры такого применения.

Примеры

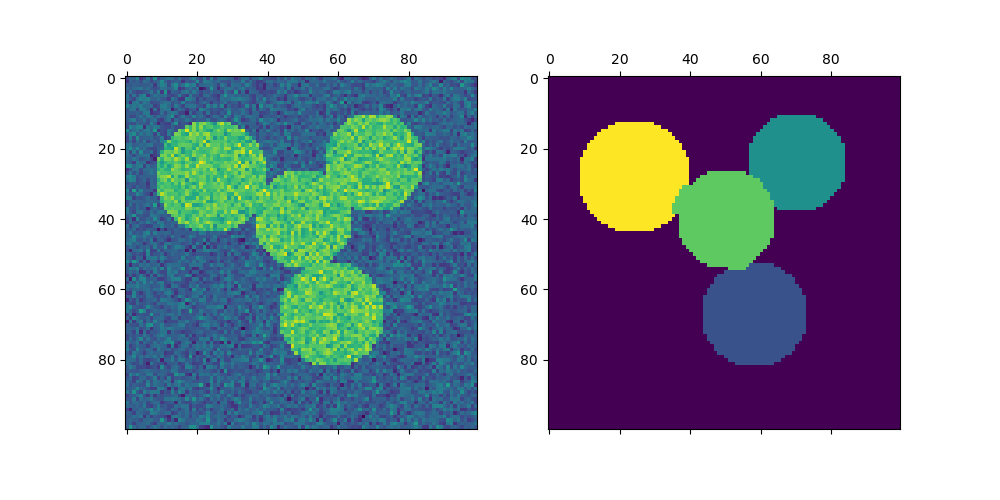
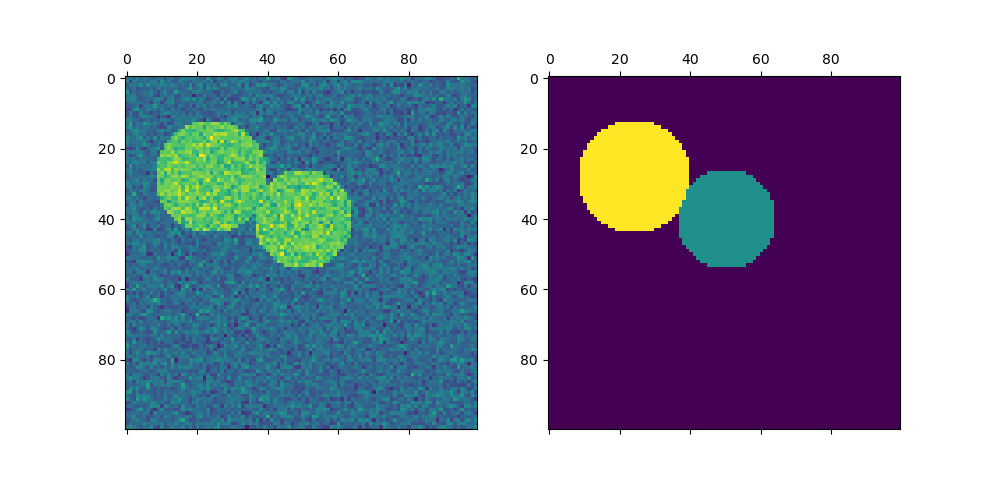
• Спектральная кластеризация для сегментации изображений: Сегментация объектов из зашумленного фона с использованием спектральной кластеризации.

• Сегментация изображения греческих монет на регионы: Спектральная кластеризация для разделения изображения монет на регионы.

2.3.5.1. Различные стратегии назначения меток

Могут использоваться различные стратегии назначения меток, соответствующие assign_labels параметр SpectralClustering. "kmeans" стратегия может соответствовать более тонким деталям, но может быть нестабильной. В частности, если вы не контролируете random_state, это может быть не воспроизводимо от запуска к запуску, так как зависит от случайной инициализации. Альтернатива "discretize" стратегия на 100% воспроизводима, но имеет тенденцию создавать участки довольно равномерной и геометрической формы. Недавно добавленная "cluster_qr" опция является детерминированной альтернативой, которая стремится создать визуально наилучшее разбиение в примере приложения ниже.

assign_labels="kmeans"	assign_labels="discretize"	assign_labels="cluster_qr"

Ссылки

• “Многоклассовая спектральная кластеризация” Stella X. Yu, Jianbo Shi, 2003

• «Простой, прямой и эффективный многомерный спектральный кластерный анализ» Анил Дамле, Виктор Минден, Лексинг Йинг, 2019

2.3.5.2. Spectral Clustering Graphs

Spectral Clustering также может использоваться для разделения графов через их спектральные вложения. В этом случае матрица сходства является матрицей смежности графа, и SpectralClustering инициализируется с affinity='precomputed':

>>> from sklearn.cluster import SpectralClustering
>>> sc = SpectralClustering(3, affinity='precomputed', n_init=100,
...                         assign_labels='discretize')
>>> sc.fit_predict(adjacency_matrix)

Ссылки

• «Учебное пособие по спектральной кластеризации» Ulrike von Luxburg, 2007

• “Normalized cuts and image segmentation” Jianbo Shi, Jitendra Malik, 2000

• «A Random Walks View of Spectral Segmentation» Марина Мейла, Цзяньбо Ши, 2001

• «О спектральной кластеризации: анализ и алгоритм» Andrew Y. Ng, Michael I. Jordan, Yair Weiss, 2001

• 'Preconditioned Spectral Clustering for Stochastic Block Partition Streaming Graph Challenge' Давид Жужунашвили, Эндрю Князев

если объекты Иерархическая кластеризация

Иерархическая кластеризация — это общее семейство алгоритмов кластеризации, которые строят вложенные кластеры, последовательно объединяя или разделяя их. Эта иерархия кластеров представляется в виде дерева (или дендрограммы). Корень дерева — это уникальный кластер, содержащий все образцы, а листья — это кластеры только с одним образцом. См. Страница Википедии для получения дополнительной информации.

The AgglomerativeClustering объект выполняет иерархическую кластеризацию с использованием подхода снизу вверх: каждое наблюдение начинается в своём собственном кластере, и кластеры последовательно объединяются. Критерий связи определяет метрику, используемую для стратегии объединения:

• Ward минимизирует сумму квадратов разностей внутри всех кластеров. Это подход, минимизирующий дисперсию, и в этом смысле он похож на целевую функцию k-средних, но решается с помощью агломеративного иерархического подхода.

• Максимум или полная связь минимизирует максимальное расстояние между наблюдениями пар кластеров.

• Средняя связь минимизирует среднее расстояний между всеми наблюдениями пар кластеров.

• Одиночная связь минимизирует расстояние между ближайшими наблюдениями пар кластеров.

AgglomerativeClustering также может масштабироваться на большое количество образцов, когда используется совместно с матрицей связности, но вычислительно дорого, когда не добавлены ограничения связности между образцами: он рассматривает на каждом шаге все возможные слияния.

FeatureAgglomeration

The FeatureAgglomeration использует агломеративную кластеризацию для группировки признаков, которые выглядят очень похожими, тем самым уменьшая количество признаков. Это инструмент снижения размерности, см. Неконтролируемое снижение размерности.

2.3.6.1. Различные типы связывания: Уорда, полное, среднее и одиночное связывание

AgglomerativeClustering поддерживает стратегии связывания Уорда, одиночного, среднего и полного.

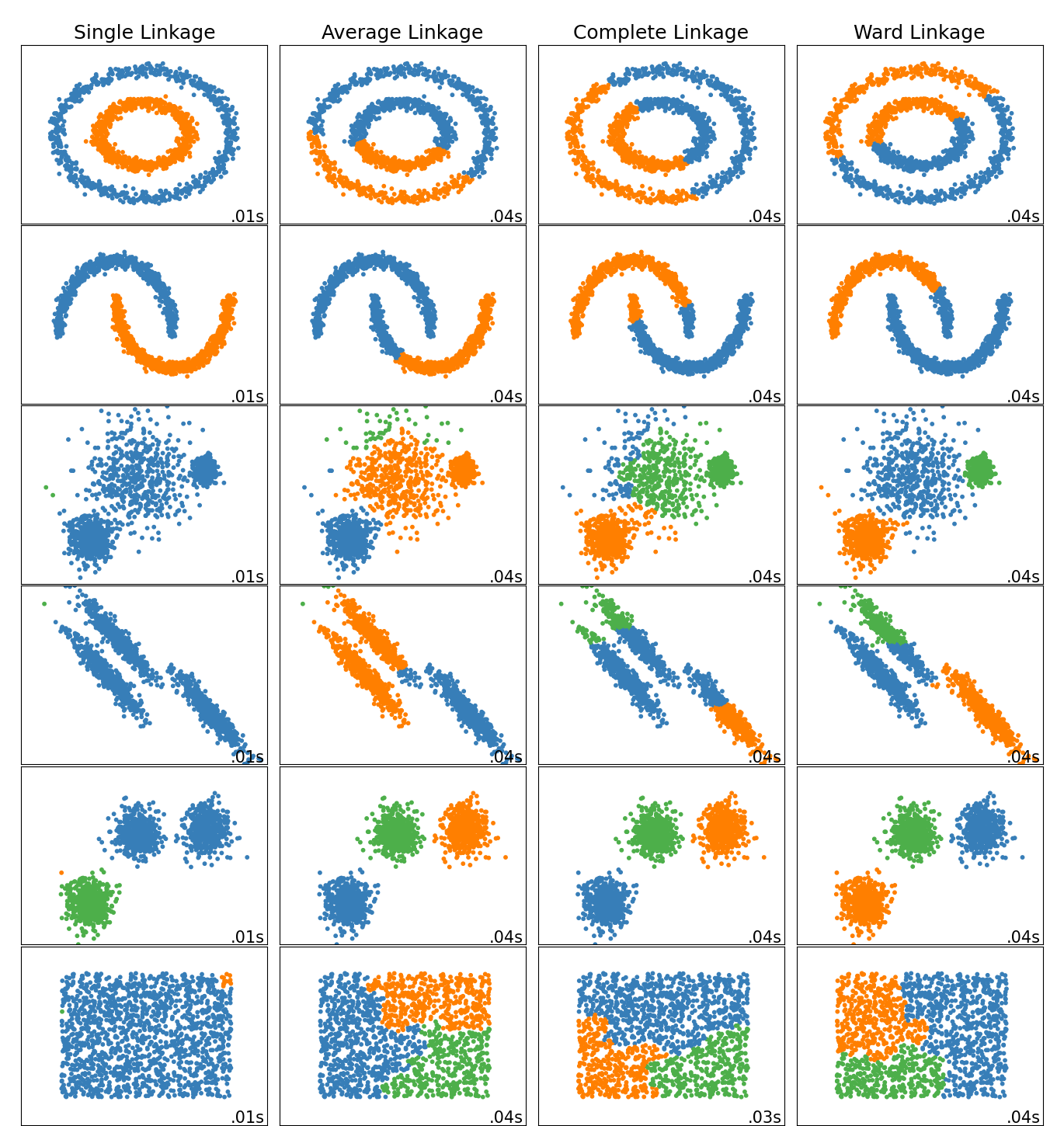
Агломеративная кластеризация имеет поведение "богатые становятся богаче", что приводит к неравномерным размерам кластеров. В этом отношении одиночная связь является наихудшей стратегией, а метод Уорда дает наиболее равномерные размеры. Однако сходство (или расстояние, используемое в кластеризации) не может быть изменено с методом Уорда, поэтому для неевклидовых метрик средняя связь является хорошей альтернативой. Одиночная связь, хотя и не устойчива к зашумленным данным, может быть вычислена очень эффективно и поэтому может быть полезна для иерархической кластеризации больших наборов данных. Одиночная связь также может хорошо работать с неглобулярными данными.

Примеры

• Различные агломеративные кластеризации на 2D-вложении цифр: исследование различных стратегий связывания на реальном наборе данных.

  • Сравнение различных методов иерархической связи на игрушечных наборах данных: исследование различных стратегий связывания в игрушечных наборах данных.

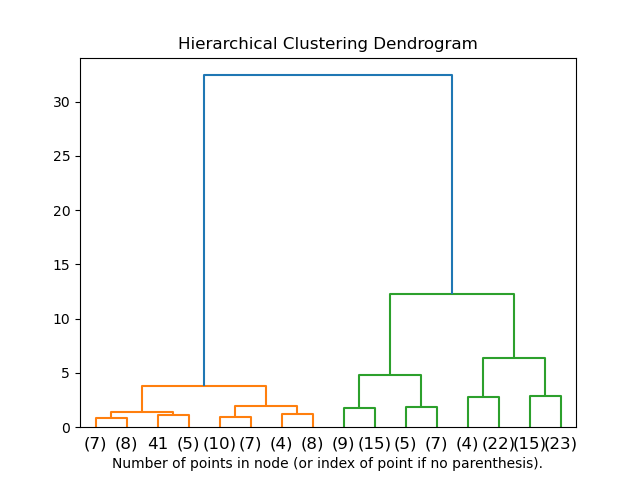
2.3.6.2. Визуализация иерархии кластеров

Можно визуализировать дерево, представляющее иерархическое слияние кластеров, в виде дендрограммы. Визуальный осмотр часто может быть полезен для понимания структуры данных, особенно в случае небольших выборок.

Примеры

• Построить дендрограмму иерархической кластеризации

2.3.6.3. Добавление ограничений связности

Интересный аспект AgglomerativeClustering заключается в том, что к этому алгоритму можно добавить ограничения связности (объединять можно только соседние кластеры) через матрицу связности, которая определяет для каждой выборки соседние выборки в соответствии с заданной структурой данных. Например, в примере со швейцарским рулетом ниже ограничения связности запрещают объединение точек, не являющихся соседними на рулете, и таким образом избегают формирования кластеров, которые простираются через перекрывающиеся слои рулета.

Эти ограничения не только полезны для наложения определенной локальной структуры, но и ускоряют алгоритм, особенно когда количество образцов велико.

Ограничения связности накладываются через матрицу связности: разреженную матрицу scipy, которая имеет элементы только на пересечении строки и столбца с индексами набора данных, которые должны быть связаны. Эта матрица может быть построена на основе априорной информации: например, вы можете захотеть кластеризовать веб-страницы, объединяя только страницы со ссылкой, указывающей с одной на другую. Она также может быть изучена из данных, например, используя sklearn.neighbors.kneighbors_graph ограничить объединение ближайшими соседями, как в этот пример, или используя sklearn.feature_extraction.image.grid_to_graph чтобы включить только слияние соседних пикселей на изображении, как в монета пример.

Предупреждение

Ограничения связности с одиночной, средней и полной связью

Ограничения связности и одиночная, полная или средняя связь могут усилить аспект «богатые становятся богаче» в агломеративной кластеризации, особенно если они построены с sklearn.neighbors.kneighbors_graph. В пределе малого количества кластеров они стремятся давать несколько макроскопически заполненных кластеров и почти пустые. (см. обсуждение в Иерархическая кластеризация со структурой и без). Одиночная связь является наиболее хрупким вариантом связи в отношении этой проблемы.

Примеры

• Демонстрация структурированной иерархической кластеризации Уорда на изображении монет: Кластеризация Уорда для разделения изображения монет на регионы.

• Иерархическая кластеризация со структурой и без: Пример алгоритма Уорда на швейцарском рулете, сравнение структурированных подходов с неструктурированными.

• Агломерация признаков против одномерного отбора: Пример снижения размерности с агломерацией признаков на основе иерархической кластеризации Уорда.

2.3.6.4. Изменение метрики

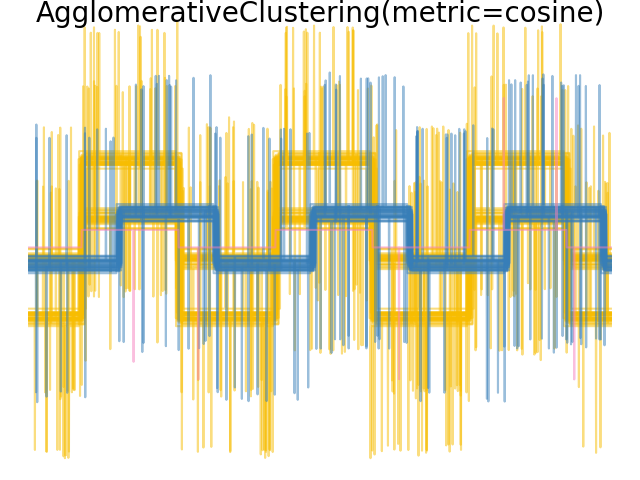
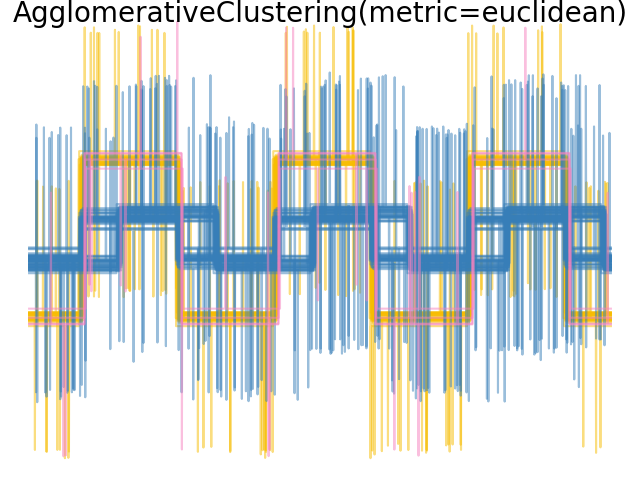
Одиночную, среднюю и полную связь можно использовать с различными расстояниями (или сходствами), в частности евклидовым расстоянием (l2), расстояние Манхэттена (или Cityblock, или l1), косинусное расстояние или любая предварительно вычисленная матрица сходства.

• l1 расстояние часто хорошо для разреженных признаков или разреженного шума: т.е. многие признаки равны нулю, как в текстовом анализе с использованием встречаемости редких слов.

• косинус расстояние интересно, потому что оно инвариантно к глобальным масштабированиям сигнала.

Рекомендации по выбору метрики заключаются в использовании той, которая максимизирует расстояние между образцами разных классов и минимизирует его внутри каждого класса.

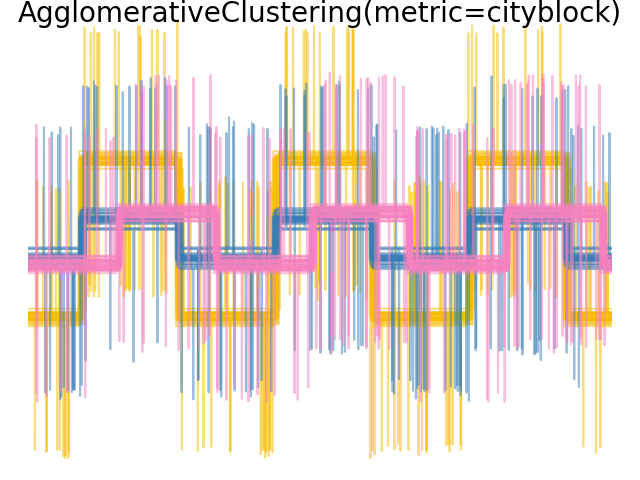
Примеры

• Агломеративная кластеризация с разными метриками

2.3.6.5. Биссекционный K-Means

The BisectingKMeans является итеративным вариантом KMeans, используя делительную иерархическую кластеризацию. Вместо создания всех центроидов сразу, центроиды выбираются постепенно на основе предыдущей кластеризации: кластер делится на два новых кластера повторно до достижения целевого количества кластеров.

BisectingKMeans более эффективен, чем KMeans когда количество кластеров велико, поскольку он работает только с подмножеством данных при каждом разбиении, в то время как KMeans всегда работает со всем набором данных.

Хотя BisectingKMeans не может воспользоваться преимуществами "k-means++" инициализация по дизайну, она все равно даст сопоставимые результаты с KMeans(init="k-means++") с точки зрения инерции при меньших вычислительных затратах и, вероятно, даст лучшие результаты, чем KMeans со случайной инициализацией.

Y. Freund и R. Schapire, «A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting», 1997.

Этот вариант также не создает пустые кластеры.

Существуют две стратегии выбора кластера для разделения:

• bisecting_strategy="largest_cluster" выбирает кластер с наибольшим количеством точек

• bisecting_strategy="biggest_inertia" выбирает кластер с наибольшей инерцией (кластер с наибольшей суммой квадратов ошибок внутри)

Выбор по наибольшему количеству точек данных в большинстве случаев даёт результат столь же точный, как выбор по инерции, и быстрее (особенно для большего количества точек данных, где вычисление ошибки может быть затратным).

Выбор по наибольшему количеству точек данных также, вероятно, создаст кластеры схожих размеров, в то время как KMeans известен тем, что создает кластеры разного размера.

Разницу между Bisecting K-Means и обычным K-Means можно увидеть на примере Сравнение производительности биссекционного K-средних и обычного K-средних. В то время как обычный алгоритм K-Means стремится создавать несвязанные кластеры, кластеры от Bisecting K-Means хорошо упорядочены и создают довольно видимую иерархию.

Ссылки

• «Сравнение методов кластеризации документов» Майкл Штайнбах, Джордж Карипис и Випин Кумар, факультет компьютерных наук и инженерии, Университет Миннесоты (июнь 2000)

• “Анализ производительности алгоритмов K-Means и Bisecting K-Means в данных веб-логов” K.Abirami и Dr.P.Mayilvahanan, International Journal of Emerging Technologies in Engineering Research (IJETER) Volume 4, Issue 8, (August 2016)

• “Алгоритм биссекционного K-средних на основе самоопределяемого K-значения и оптимизации центров кластеризации” Цзянь Ди, Синьюэ Го, Школа управления и компьютерной инженерии, Северо-Китайский университет электроэнергетики, Баодин, Хэбэй, Китай (август 2017)

2.3.7. DBSCAN

The DBSCAN алгоритм рассматривает кластеры как области высокой плотности, разделённые областями низкой плотности. Из-за этого довольно общего взгляда кластеры, найденные DBSCAN, могут иметь любую форму, в отличие от k-means, который предполагает, что кластеры имеют выпуклую форму. Ключевым компонентом DBSCAN является концепция основные выборки, которые являются образцами в областях высокой плотности. Кластер, следовательно, представляет собой набор основных образцов, каждый близкий друг к другу (измеряемый некоторой метрикой расстояния) и набор неосновных образцов, которые близки к основному образцу (но сами не являются основными образцами). В алгоритме есть два параметра, min_samples и eps, которые формально определяют, что мы имеем в виду, когда говорим dense. Выше min_samples или ниже eps указывают на более высокую плотность, необходимую для формирования кластера.

Более формально мы определяем основную выборку как выборку в наборе данных, такую что существует min_samples других образцов в пределах расстояния eps, которые определены как соседи основного образца. Это говорит нам, что основной образец находится в плотной области векторного пространства. Кластер - это набор основных образцов, который может быть построен рекурсивным взятием основного образца, нахождением всех его соседей, которые являются основными образцами, нахождением всех их соседей, которые являются основными образцами, и так далее. Кластер также имеет набор неосновных образцов, которые являются соседями основного образца в кластере, но сами не являются основными образцами. Интуитивно, эти образцы находятся на окраинах кластера.

Любой основной образец по определению является частью кластера. Любой образец, который не является основным образцом и находится хотя бы eps в расстоянии от любого основного образца, считается выбросом алгоритмом.

Хотя параметр min_samples в основном контролирует, насколько алгоритм устойчив к шуму (на зашумленных и больших наборах данных может быть желательно увеличить этот параметр), параметр eps является критически важно выбрать соответствующим образом для набора данных и функции расстояния и обычно не может быть оставлен со значением по умолчанию. Он контролирует локальную окрестность точек. Если выбран слишком маленьким, большинство данных вообще не будет кластеризовано (и помечено как -1 для «шума»). Если выбрано слишком большое значение, это приводит к слиянию близких кластеров в один кластер и в конечном итоге к возврату всего набора данных как одного кластера. В литературе обсуждались некоторые эвристики для выбора этого параметра, например, основанные на «колене» на графике расстояний ближайших соседей (как обсуждается в ссылках ниже).

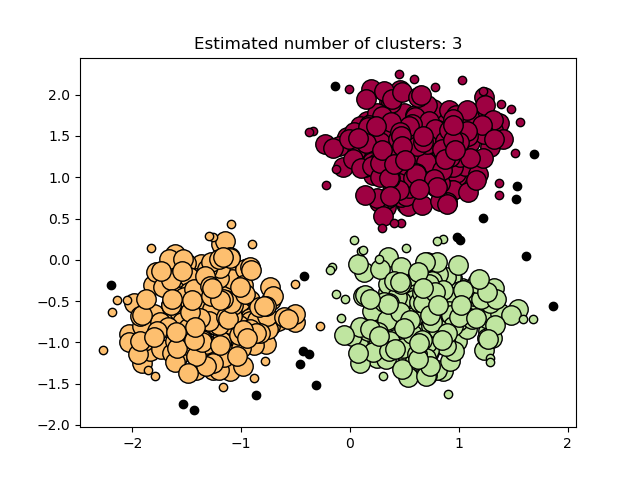
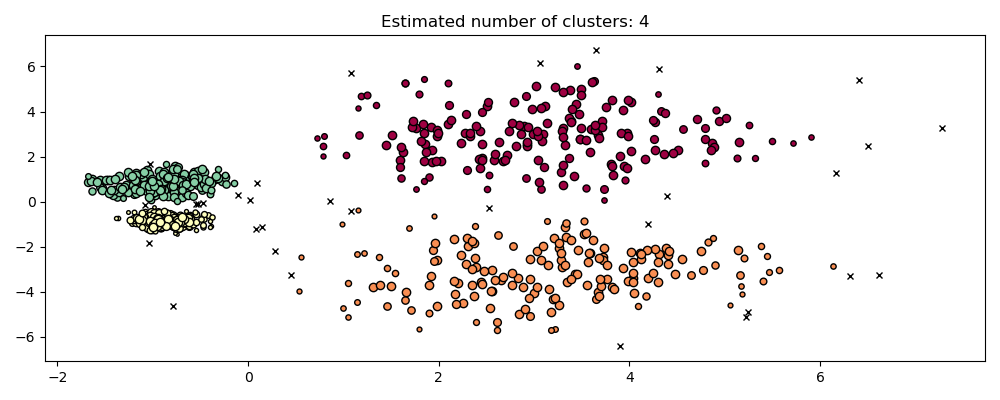
На рисунке ниже цвет указывает на принадлежность к кластеру, причём большие круги обозначают основные образцы, найденные алгоритмом. Меньшие круги — это неосновные образцы, которые всё ещё входят в кластер. Кроме того, выбросы обозначены чёрными точками ниже.

Примеры

• Демонстрация алгоритма кластеризации DBSCAN

Реализация

Алгоритм DBSCAN детерминирован и всегда генерирует одни и те же кластеры при одинаковых данных в том же порядке. Однако результаты могут различаться, когда данные предоставляются в другом порядке. Во-первых, хотя основные образцы всегда будут назначены одним и тем же кластерам, метки этих кластеров будут зависеть от порядка, в котором эти образцы встречаются в данных. Во-вторых, и что более важно, кластеры, к которым назначены неосновные образцы, могут различаться в зависимости от порядка данных. Это происходит, когда неосновной образец имеет расстояние меньше eps к двум основным образцам в разных кластерах. По неравенству треугольника, эти два основных образца должны быть более удаленными, чем eps друг от друга, иначе они были бы в одном кластере. Неосновной образец присваивается тому кластеру, который генерируется первым при проходе по данным, поэтому результаты будут зависеть от порядка данных.

Текущая реализация использует ball trees и kd-trees для определения окрестности точек, что позволяет избежать вычисления полной матрицы расстояний (как это делалось в версиях scikit-learn до 0.14). Возможность использования пользовательских метрик сохранена; подробности см. в NearestNeighbors.

Потребление памяти для больших размеров выборки

Эта реализация по умолчанию не является эффективной по памяти, поскольку она строит полную матрицу попарного сходства в случаях, когда kd-деревья или ball-деревья не могут быть использованы (например, с разреженными матрицами). Эта матрица будет потреблять \(n^2\) числа с плавающей точкой. Несколько механизмов для обхода этого:

• Используйте OPTICS кластеризация в сочетании с extract_dbscan метод. Кластеризация OPTICS также вычисляет полную попарную матрицу, но хранит в памяти только одну строку за раз (сложность по памяти \(\mathcal{O}(n)\)).

• Разреженный граф окрестностей по радиусу (где отсутствующие элементы считаются вне eps) может быть предварительно вычислен эффективно по памяти, и dbscan может быть запущен над ним с metric='precomputed'. См. sklearn.neighbors.NearestNeighbors.radius_neighbors_graph.

• Набор данных может быть сжат, либо путем удаления точных дубликатов, если они встречаются в ваших данных, либо с помощью BIRCH. Тогда у вас есть относительно небольшое количество представителей для большого количества точек. Затем вы можете предоставить sample_weight при обучении DBSCAN.

Ссылки

• Алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом Эстер, М., Х. П. Кригель, Дж. Сандер и К. Сюй, В материалах 2-й Международной конференции по обнаружению знаний и интеллектуальному анализу данных, Портленд, Орегон, AAAI Press, стр. 226-231. 1996.

• DBSCAN пересмотрен, пересмотрен: почему и как вам следует (все еще) использовать DBSCAN. данные, даже с правилами повышения типа NumPy 2.

2.3.8. HDBSCAN

The HDBSCAN алгоритм можно рассматривать как расширение DBSCAN и OPTICS. Конкретно, DBSCAN предполагает, что критерий кластеризации (т.е. требование плотности) является глобально однородный. Другими словами, DBSCAN может испытывать трудности с успешным захватом кластеров с разной плотностью. HDBSCAN pair_confusion_matrix

Примечание

Эта реализация адаптирована из оригинальной реализации HDBSCAN, scikit-learn-contrib/hdbscan на основе [LJ2017].

Примеры

• Демонстрация алгоритма кластеризации HDBSCAN

2.3.8.1. Граф взаимной достижимости

HDBSCAN сначала определяет \(d_c(x_p)\), базовое расстояние выборки \(x_p\), как расстояние до его min_samples k-й ближайший сосед, считая себя. Например, если min_samples=5 и \(x_*\) является 5-м ближайшим соседом для \(x_p\) тогда основное расстояние равно:

\[d_c(x_p)=d(x_p, x_*).\]

Далее определяется \(d_m(x_p, x_q)\), взаимная достижимая дистанция двух точек \(x_p, x_q\), как:

\[d_m(x_p, x_q) = \max\{d_c(x_p), d_c(x_q), d(x_p, x_q)\}\]

Эти два понятия позволяют нам построить граф взаимной достижимости \(G_{ms}\) определено для фиксированного выбора min_samples связывая каждый образец \(x_p\) с вершиной графа, и, следовательно, рёбрами между точками \(x_p, x_q\) являются расстояниями взаимной достижимости \(d_m(x_p, x_q)\) между ними. Мы можем построить подмножества этого графа, обозначаемые как \(G_{ms,\varepsilon}\), удаляя любые ребра со значением больше \(\varepsilon\): из исходного графа. Любые точки, чьё ядерное расстояние меньше \(\varepsilon\)На этом этапе помечены как шум. Оставшиеся точки затем кластеризуются путем нахождения связных компонент этого обрезанного графа.

Примечание

Взятие связных компонент обрезанного графа \(G_{ms,\varepsilon}\) эквивалентно запуску DBSCAN* с min_samples и \(\varepsilon\). DBSCAN* — это слегка измененная версия DBSCAN, упомянутая в [CM2013].

2.3.8.2. Иерархическая кластеризация

HDBSCAN можно рассматривать как алгоритм, выполняющий кластеризацию DBSCAN* для всех значений \(\varepsilon\). Как упоминалось ранее, это эквивалентно нахождению связных компонентов графов взаимной достижимости для всех значений \(\varepsilon\)Для эффективного выполнения этого HDBSCAN сначала извлекает минимальное остовное дерево (MST) из полностью связного графа взаимной достижимости, затем жадным образом обрезает ребра с наибольшим весом. Общий алгоритм HDBSCAN выглядит следующим образом:

1. Извлечь MST из \(G_{ms}\).

2. Расширьте MST, добавив «саморебро» для каждой вершины с весом, равным основному расстоянию базового образца.

3. Инициализация одного кластера и метки для MST.

4. Удалите ребро с наибольшим весом из MST (связи удаляются одновременно).

5. Назначьте метки кластеров связанным компонентам, которые содержат конечные точки теперь удаленного ребра. Если компонент не имеет хотя бы одного ребра, ему вместо этого назначается метка «null», отмечающая его как шум.

6. Повторяйте 4-5, пока не останется больше связных компонент.

Таким образом, HDBSCAN способен получить все возможные разбиения, достижимые с помощью DBSCAN* для фиксированного выбора min_samples иерархическим образом. Действительно, это позволяет HDBSCAN выполнять кластеризацию при различных плотностях и, таким образом, ему больше не требуется \(\varepsilon\) должен быть задан как гиперпараметр. Вместо этого он полагается исключительно на выбор min_samples, что обычно является более устойчивым гиперпараметром.

HDBSCAN можно сгладить с помощью дополнительного гиперпараметра min_cluster_size который указывает, что во время иерархической кластеризации компоненты с менее чем minimum_cluster_size многие образцы считаются шумом. На практике можно установить minimum_cluster_size = min_samples для связи параметров и упрощения пространства гиперпараметров.

Ссылки

[CM2013]

Campello, R.J.G.B., Moulavi, D., Sander, J. (2013). Density-Based Clustering Based on Hierarchical Density Estimates. В: Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G. (ред.) Advances in Knowledge Discovery and Data Mining. PAKDD 2013. Lecture Notes in Computer Science(), том 7819. Springer, Berlin, Heidelberg. Кластеризация на основе плотности с использованием иерархических оценок плотности

[LJ2017]

L. McInnes и J. Healy, (2017). Ускоренная иерархическая кластеризация на основе плотности. В: IEEE International Conference on Data Mining Workshops (ICDMW), 2017, стр. 33-42. Ускоренная иерархическая кластеризация на основе плотности

2.3.9. OPTICS

The OPTICS алгоритм имеет много общего с DBSCAN алгоритм, и может рассматриваться как обобщение DBSCAN, которое ослабляет eps требование от одного значения до диапазона значений. Ключевое различие между DBSCAN и OPTICS заключается в том, что алгоритм OPTICS строит достижимость граф, который присваивает каждому образцу как reachability_ расстояние, и точка внутри кластера ordering_ атрибут; эти два атрибута назначаются при обучении модели и используются для определения принадлежности к кластеру. Если OPTICS запускается со значением по умолчанию inf набор для max_eps, тогда извлечение кластеров в стиле DBSCAN может выполняться многократно за линейное время для любого заданного eps значение с использованием cluster_optics_dbscan метод. Установка max_eps установка меньшего значения приведет к сокращению времени выполнения и может рассматриваться как максимальный радиус окрестности от каждой точки для поиска других потенциально достижимых точек.

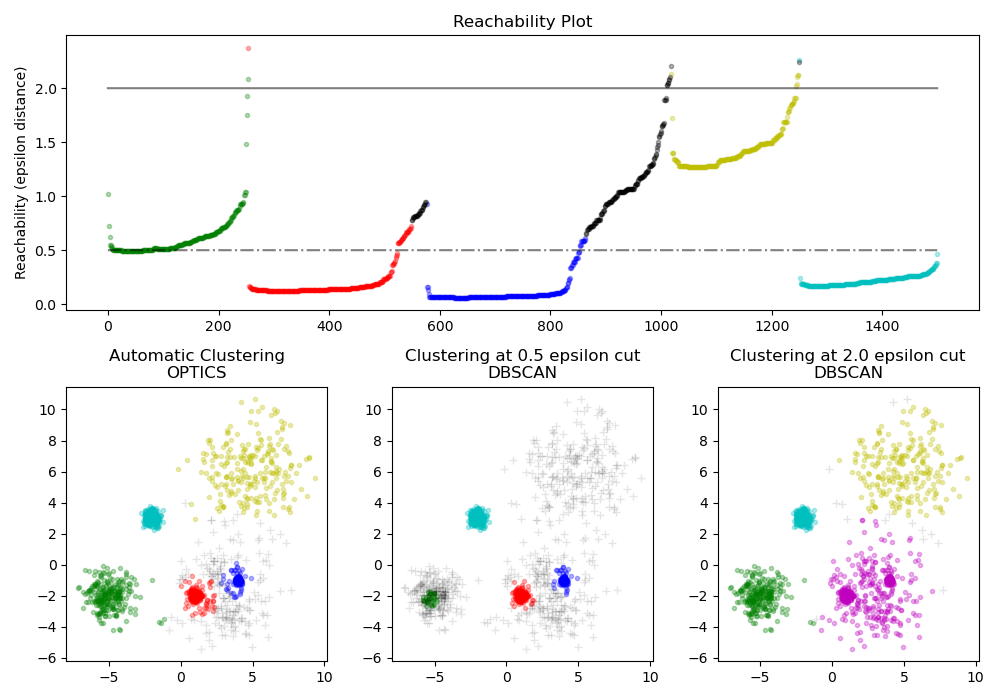
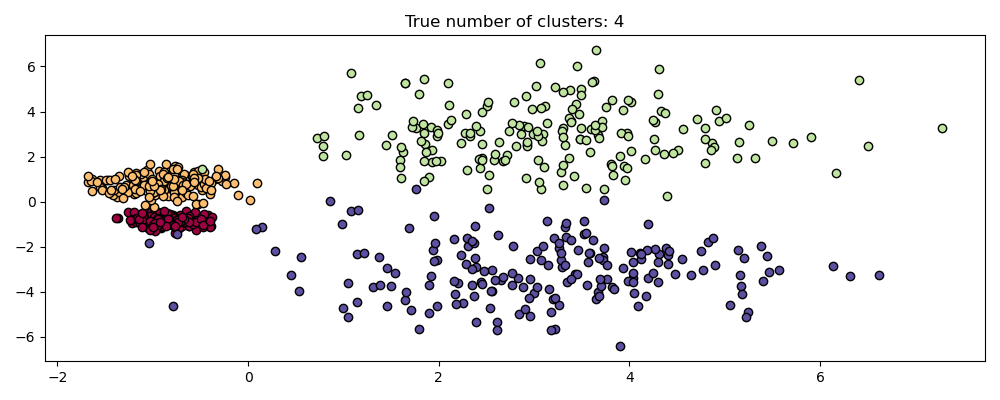
The достижимость расстояния, сгенерированные OPTICS, позволяют извлекать кластеры с переменной плотностью в одном наборе данных. Как показано на графике выше, объединение достижимость расстояния и набор данных ordering_ создаёт график достижимости, где плотность точек представлена на оси Y, и точки упорядочены так, что соседние точки являются смежными. 'Разрез' графика достижимости при одном значении дает результаты, подобные DBSCAN; все точки выше 'разреза' классифицируются как шум, и каждый раз, когда при чтении слева направо происходит разрыв, это означает новый кластер. Извлечение кластеров по умолчанию с OPTICS смотрит на крутые склоны внутри графика, чтобы найти кластеры, и пользователь может определить, что считается крутым склоном, используя параметр xi. Также существуют другие возможности для анализа самого графа, такие как генерация иерархических представлений данных через дендрограммы достижимости, а иерархия кластеров, обнаруженных алгоритмом, может быть доступна через cluster_hierarchy_ параметр. График выше раскрашен так, что цвета кластеров в плоском пространстве соответствуют линейным сегментам кластеров на графике достижимости. Обратите внимание, что синий и красный кластеры смежны на графике достижимости и могут быть иерархически представлены как дочерние элементы большего родительского кластера.

Примеры

• Демонстрация алгоритма кластеризации OPTICS

Сравнение с DBSCAN

Результаты из OPTICS cluster_optics_dbscan метод и DBSCAN очень похожи, но не всегда идентичны; в частности, маркировка периферийных и шумовых точек. Это отчасти связано с тем, что первые образцы каждой плотной области, обработанные OPTICS, имеют большое значение достижимости, находясь близко к другим точкам в своей области, и поэтому иногда будут помечены как шум, а не как периферия. Это влияет на соседние точки, когда они рассматриваются как кандидаты на маркировку как периферия или шум.

Обратите внимание, что для любого отдельного значения eps, DBSCAN будет иметь меньшее время выполнения, чем OPTICS; однако для повторных запусков с различными eps значениям, один запуск OPTICS может потребовать меньше совокупного времени выполнения, чем DBSCAN. Также важно отметить, что вывод OPTICS близок к выводу DBSCAN только если eps и max_eps близки.

Вычислительная сложность

Пространственные индексные деревья используются, чтобы избежать вычисления полной матрицы расстояний, и позволяют эффективно использовать память на больших наборах образцов. Различные метрики расстояния могут быть предоставлены через metric ключевое слово.

Для больших наборов данных можно получить похожие (но не идентичные) результаты с помощью HDBSCANРеализация HDBSCAN является многопоточной и имеет лучшую алгоритмическую сложность времени выполнения по сравнению с OPTICS, ценой худшего масштабирования памяти. Для очень больших наборов данных, которые исчерпывают системную память при использовании HDBSCAN, OPTICS сохранит \(n\) (в отличие от \(n^2\)) масштабирование памяти; однако, настройка max_eps Параметр, вероятно, потребуется использовать для получения решения за разумное время.

Ссылки

• “OPTICS: ordering points to identify the clustering structure.” Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. In ACM Sigmod Record, vol. 28, no. 2, pp. 49-60. ACM, 1999.

2.3.10. BIRCH

The Birch строит дерево, называемое деревом характеристик кластеризации (CFT) для заданных данных. Данные по сути сжимаются с потерями в набор узлов характеристик кластеризации (CF Nodes). Узлы CF имеют несколько подкластеров, называемых подкластерами характеристик кластеризации (CF Subclusters), и эти подкластеры CF, расположенные в нетерминальных узлах CF, могут иметь узлы CF в качестве дочерних элементов.

CF Subclusters содержат необходимую информацию для кластеризации, что предотвращает необходимость хранения всех входных данных в памяти. Эта информация включает:

• Количество образцов в подкластере.

• Линейная сумма - n-мерный вектор, содержащий сумму всех выборок

• Квадрат суммы - сумма квадратов L2 нормы всех образцов.

• Центроиды — чтобы избежать пересчета линейной суммы / n_samples.

• Квадрат нормы центроидов.

Алгоритм BIRCH имеет два параметра: порог и коэффициент ветвления. Коэффициент ветвления ограничивает количество подкластеров в узле, а порог ограничивает расстояние между входящей выборкой и существующими подкластерами.

Этот алгоритм можно рассматривать как пример метода сокращения данных, поскольку он сокращает входные данные до набора подкластеров, которые получены непосредственно из листьев CFT. Эти сокращённые данные можно дополнительно обработать, передав их в глобальный кластеризатор. Этот глобальный кластеризатор может быть задан с помощью n_clusters. Если n_clusters установлен в None, подкластеры из листьев напрямую считываются, в противном случае глобальный шаг кластеризации помечает эти подкластеры в глобальные кластеры (метки), и выборки отображаются в глобальную метку ближайшего подкластера.

Описание алгоритма

• Новый образец вставляется в корень CF-дерева, который является CF-узлом. Затем он объединяется с подкластером корня, имеющим наименьший радиус после объединения, с учётом условий порога и коэффициента ветвления. Если подкластер имеет какой-либо дочерний узел, то это повторяется до достижения листа. После нахождения ближайшего подкластера в листе свойства этого подкластера и родительских подкластеров рекурсивно обновляются.

• Если радиус подкластера, полученного объединением нового образца и ближайшего подкластера, больше квадрата порога и если количество подкластеров больше коэффициента ветвления, то пространство временно выделяется для этого нового образца. Два наиболее удаленных подкластера выбираются, и подкластеры делятся на две группы на основе расстояния между ними.

• Если этот узел разделения имеет родительский субкластер и есть место для нового субкластера, то родитель разделяется на два. Если места нет, то этот узел снова разделяется на два, и процесс продолжается рекурсивно, пока не достигнет корня.

BIRCH или MiniBatchKMeans?

• BIRCH не очень хорошо масштабируется на данные высокой размерности. Как правило, если n_features больше двадцати, обычно лучше использовать MiniBatchKMeans.

• Если количество экземпляров данных необходимо уменьшить или если требуется большое количество подкластеров либо в качестве шага предварительной обработки, либо по другим причинам, BIRCH более полезен, чем MiniBatchKMeans.

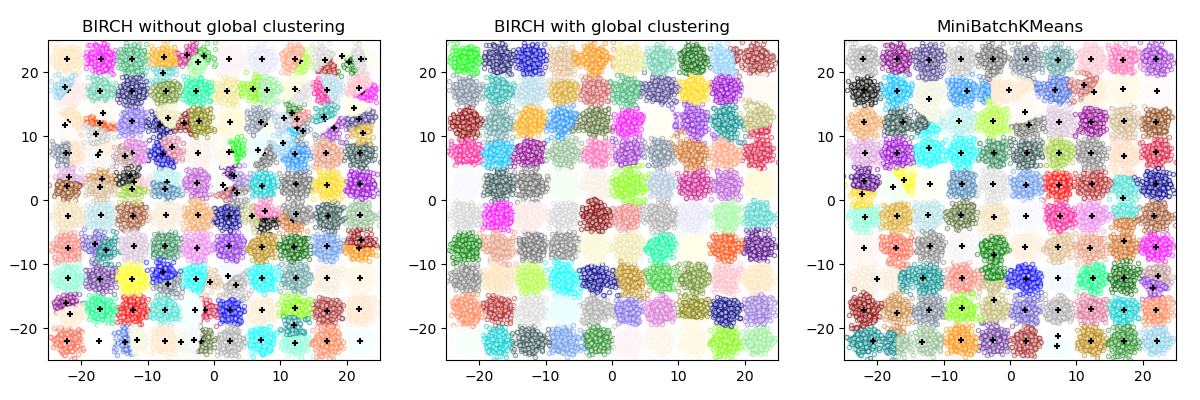
Как использовать partial_fit?

Чтобы избежать вычисления глобальной кластеризации при каждом вызове partial_fit пользователю рекомендуется:

1. Чтобы установить n_clusters=None изначально.

2. Обучить все данные несколькими вызовами partial_fit.

3. Установить n_clusters к требуемому значению с помощью brc.set_params(n_clusters=n_clusters).

4. Вызов partial_fit наконец, без аргументов, т.е. brc.partial_fit() который выполняет глобальную кластеризацию.

Ссылки

• Тиан Чжан, Рагху Рамакришнан, Марон Ливни BIRCH: Эффективный метод кластеризации данных для больших баз данных. https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf

• Roberto Perdisci JBirch - Java-реализация алгоритма кластеризации BIRCH https://code.google.com/archive/p/jbirch

2.3.11. Оценка производительности кластеризации

Оценка производительности алгоритма кластеризации не так тривиальна, как подсчет количества ошибок или точности и полноты алгоритма контролируемой классификации. В частности, любая метрика оценки не должна учитывать абсолютные значения меток кластеров, а скорее определяет ли эта кластеризация разделения данных, аналогичные некоторому эталонному набору классов или удовлетворяющие некоторому предположению, такому что члены одного класса более похожи, чем члены разных классов, согласно некоторой метрике сходства.

2.3.11.1. Индекс Рэнда

При известных истинных назначениях классов labels_true и назначениями нашего алгоритма кластеризации тех же образцов labels_pred, (скорректированный или нескорректированный) индекс Рэнда является функцией, измеряющей similarity двух назначений, игнорируя перестановки:

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.rand_score(labels_true, labels_pred)
0.66

Индекс Рэнда не гарантирует получение значения, близкого к 0.0, для случайной разметки. Скорректированный индекс Рэнда корректирует на случайность и даст такую базовую линию.

>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

Как и со всеми метриками кластеризации, можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.rand_score(labels_true, labels_pred)
0.66
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24

Кроме того, оба rand_score и adjusted_rand_score являются symmetric: перестановка аргумента не меняет оценки. Таким образом, они могут использоваться как меры консенсуса:

>>> metrics.rand_score(labels_pred, labels_true)
0.66
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24

Идеальная разметка оценивается в 1.0:

>>> labels_pred = labels_true[:]
>>> metrics.rand_score(labels_true, labels_pred)
1.0
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0

Плохо согласующиеся метки (например, независимые разметки) имеют более низкие оценки, и для скорректированного индекса Рэнда оценка будет отрицательной или близкой к нулю. Однако для нескорректированного индекса Рэнда оценка, хотя и ниже, не обязательно будет близка к нулю:

>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1]
>>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6]
>>> metrics.rand_score(labels_true, labels_pred)
0.39
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.072

Преимущества:

• Интерпретируемость: нескорректированный индекс Рэнда пропорционален количеству пар образцов, метки которых одинаковы в обоих labels_pred и labels_true, или различаются в обоих.

• Случайные (равномерные) назначения меток имеют скорректированный индекс Рэнда, близкий к 0.0 для любого значения n_clusters и n_samples (что не относится к нескорректированному индексу Рэнда или V-меры, например).

• Ограниченный диапазон: Меньшие значения указывают на различные разметки, схожие кластеризации имеют высокий (скорректированный или нескорректированный) индекс Рэнда, 1.0 — это идеальный показатель соответствия. Диапазон оценки — [0, 1] для нескорректированного индекса Рэнда и [-0.5, 1] для скорректированного индекса Рэнда.

• Не делается никаких предположений о структуре кластера: (Скорректированный или нескорректированный) индекс Рэнда может использоваться для сравнения всех видов алгоритмов кластеризации и может применяться для сравнения алгоритмов кластеризации, таких как k-means, который предполагает изотропные формы кластеров, с результатами спектральных алгоритмов кластеризации, которые могут находить кластеры со "сложенными" формами.

Недостатки:

• В отличие от инерции, (скорректированный или нескорректированный) индекс Rand требует знания истинных классов что почти никогда не доступно на практике или требует ручного назначения человеком-аннотатором (как в настройке обучения с учителем).

  Однако (скорректированный или нескорректированный) индекс Рэнда также может быть полезен в чисто неконтролируемой настройке как строительный блок для индекса консенсуса, который может быть использован для выбора модели кластеризации (TODO).

• The нескорректированный индекс Рэнда часто близок к 1.0 даже если сами кластеризации значительно различаются. Это можно понять, интерпретируя индекс Рэнда как точность маркировки пар элементов, полученную из кластеризаций: на практике часто существует большинство пар элементов, которым присвоен different метка пары как в предсказанной, так и в истинной кластеризации, что приводит к высокой доле совпадающих меток пар, что впоследствии дает высокий балл.

Примеры

• Коррекция на случайность в оценке производительности кластеризации: Анализ влияния размера набора данных на значение мер кластеризации для случайных назначений.

Математическая формулировка

Если C — это истинное назначение классов, а K — кластеризация, определим \(a\) и \(b\) как:

• \(a\), количество пар элементов, которые находятся в одном множестве в C и в одном множестве в K

• \(b\)количество пар элементов, которые находятся в разных множествах в C и в разных множествах в K

Некорректированный индекс Рэнда тогда задается как:

\[\text{RI} = \frac{a + b}{C_2^{n_{samples}}}\]

где \(C_2^{n_{samples}}\) это общее количество возможных пар в наборе данных. Не имеет значения, выполняется ли расчет на упорядоченных парах или неупорядоченных парах, если расчет выполняется последовательно.

Однако индекс Рэнда не гарантирует, что случайные назначения меток получат значение, близкое к нулю (особенно если количество кластеров того же порядка величины, что и количество образцов).

Чтобы противодействовать этому эффекту, мы можем дисконтировать ожидаемый RI \(E[\text{RI}]\) случайных маркировок путём определения скорректированного индекса Рэнда следующим образом:

\[\text{ARI} = \frac{\text{RI} - E[\text{RI}]}{\max(\text{RI}) - E[\text{RI}]}\]

Ссылки

• Сравнение разделов L. Hubert и P. Arabie, Journal of Classification 1985

• Свойства скорректированного индекса Рэнда Хьюберта-Араби D. Steinley, Psychological Methods 2004

• Запись в Википедии для индекса Рэнда

• Минимальный скорректированный индекс Рэнда для двух кластеризаций заданного размера, 2022, J. E. Chacón и A. I. Rastrojo

2.3.11.2. Оценки на основе взаимной информации

При известных истинных назначениях классов labels_true и назначения нашего алгоритма кластеризации тех же образцов labels_pred, Mutual Information является функцией, измеряющей согласие двух назначений, игнорируя перестановки. Доступны две разные нормализованные версии этой меры, Нормализованная взаимная информация (NMI) и Скорректированная взаимная информация (AMI). NMI часто используется в литературе, в то время как AMI был предложен недавно и является нормализованный относительно случайности:

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:

>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504

All, mutual_info_score, adjusted_mutual_info_score и normalized_mutual_info_score симметричны: перестановка аргументов не меняет оценку. Таким образом, они могут использоваться как мера консенсуса:

>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504

Идеальная разметка оценивается в 1.0:

>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0

>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0

Это неверно для mutual_info_score, что, следовательно, сложнее оценить:

>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69

Плохие (например, независимые разметки) имеют неположительные оценки:

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526

Преимущества:

• Случайные (равномерные) назначения меток имеют оценку AMI близкую к 0.0 для любого значения n_clusters и n_samples (что не относится к сырой взаимной информации или V-мере, например).

• Верхняя граница 1: Значения, близкие к нулю, указывают на два назначения меток, которые в основном независимы, в то время как значения, близкие к единице, указывают на значительное согласие. Кроме того, AMI, равный точно 1, указывает, что два назначения меток равны (с перестановкой или без).

Недостатки:

• В отличие от инерции, Меры на основе взаимной информации требуют знания истинных классов в то время как почти никогда не доступен на практике или требует ручного назначения человеком-аннотатором (как в настройке обучения с учителем).

  Однако меры на основе MI также могут быть полезны в чисто неконтролируемой настройке как строительный блок для индекса консенсуса, который может использоваться для выбора модели кластеризации.

• NMI и MI не скорректированы на случайность.

Примеры

• Коррекция на случайность в оценке производительности кластеризации: Анализ влияния размера набора данных на значение мер кластеризации для случайных назначений. Этот пример также включает скорректированный индекс Рэнда.

Математическая формулировка

Предположим два назначения меток (для тех же N объектов), \(U\) и \(V\). Их энтропия - это количество неопределенности для набора разделов, определяемое:

\[H(U) = - \sum_{i=1}^{|U|}P(i)\log(P(i))\]

где \(P(i) = |U_i| / N\) — это вероятность того, что объект, выбранный случайным образом из \(U\) относится к классу \(U_i\). Аналогично для \(V\):

\[H(V) = - \sum_{j=1}^{|V|}P'(j)\log(P'(j))\]

С \(P'(j) = |V_j| / N\). Взаимная информация (MI) между \(U\) и \(V\) рассчитывается по формуле:

\[\text{MI}(U, V) = \sum_{i=1}^{|U|}\sum_{j=1}^{|V|}P(i, j)\log\left(\frac{P(i,j)}{P(i)P'(j)}\right)\]

где \(P(i, j) = |U_i \cap V_j| / N\) это вероятность того, что случайно выбранный объект попадает в оба класса \(U_i\) и \(V_j\).

Это также может быть выражено в формулировке мощности множества:

\[\text{MI}(U, V) = \sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \frac{|U_i \cap V_j|}{N}\log\left(\frac{N|U_i \cap V_j|}{|U_i||V_j|}\right)\]

Нормализованная взаимная информация определяется как

\[\text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))}\]

Это значение взаимной информации, а также нормализованный вариант не скорректированы на случайность и будут стремиться увеличиваться с ростом количества различных меток (кластеров), независимо от фактического количества "взаимной информации" между назначениями меток.

Ожидаемое значение для взаимной информации может быть рассчитано с использованием следующего уравнения [VEB2009]. В этом уравнении, \(a_i = |U_i|\) (количество элементов в \(U_i\)) и \(b_j = |V_j|\) (количество элементов в \(V_j\)).

\[E[\text{MI}(U,V)]=\sum_{i=1}^{|U|} \sum_{j=1}^{|V|} \sum_{n_{ij}=(a_i+b_j-N)^+ }^{\min(a_i, b_j)} \frac{n_{ij}}{N}\log \left( \frac{ N.n_{ij}}{a_i b_j}\right) \frac{a_i!b_j!(N-a_i)!(N-b_j)!}{N!n_{ij}!(a_i-n_{ij})!(b_j-n_{ij})! (N-a_i-b_j+n_{ij})!}\]

Используя ожидаемое значение, скорректированная взаимная информация может быть рассчитана по аналогичной формуле с скорректированным индексом Рэнда:

\[\text{AMI} = \frac{\text{MI} - E[\text{MI}]}{\text{mean}(H(U), H(V)) - E[\text{MI}]}\]

Для нормализованной взаимной информации и скорректированной взаимной информации нормализующее значение обычно является некоторым обобщённый среднее значение энтропий каждого кластеризации. Существуют различные обобщённые средние, и нет строгих правил для предпочтения одного другому. Решение во многом зависит от области; например, в обнаружении сообществ наиболее распространено арифметическое среднее. Каждый метод нормализации обеспечивает «качественно схожее поведение» [YAT2016]. В нашей реализации это контролируется параметром average_method параметр.

Винь и др. (2010) назвали варианты NMI и AMI по их методу усреднения [VEB2010]Их средние значения 'sqrt' и 'sum' являются геометрическим и арифметическим средними; мы используем эти более распространенные названия.

Ссылки

• Strehl, Alexander, and Joydeep Ghosh (2002). “Cluster ensembles - a knowledge reuse framework for combining multiple partitions”. Journal of Machine Learning Research 3: 583-617. doi:10.1162/153244303321897735.

• Запись в Википедии о (нормализованной) взаимной информации

• Запись в Википедии для скорректированной взаимной информации

[VEB2009]

Vinh, Epps, and Bailey, (2009). "Information theoretic measures for clusterings comparison". Proceedings of the 26th Annual International Conference on Machine Learning - ICML '09. doi:10.1145/1553374.1553511. ISBN 9781605585161.

[VEB2010]

Vinh, Epps, and Bailey, (2010). "Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance". JMLR <https://jmlr.csail.mit.edu/papers/volume11/vinh10a/vinh10a.pdf>

[YAT2016]

Ян, Альгесхаймер и Тессон, (2016). «Сравнительный анализ алгоритмов обнаружения сообществ на искусственных сетях». Scientific Reports 6: 30750. doi:10.1038/srep30750.

2.3.11.3. Однородность, полнота и V-мера

Учитывая знание истинных назначений классов образцов, можно определить некоторую интуитивную метрику, используя анализ условной энтропии.

В частности, Розенберг и Хиршберг (2007) определяют следующие две желательные цели для любого назначения кластера:

• гомогенность: каждый кластер содержит только элементы одного класса.

• полнота: все элементы данного класса назначаются в один кластер.

Мы можем превратить эти концепции в оценки homogeneity_score и completeness_score. Оба ограничены снизу 0.0 и сверху 1.0 (чем выше, тем лучше):

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66

>>> metrics.completeness_score(labels_true, labels_pred)
0.42

Их среднее гармоническое, называемое V-мера вычисляется с помощью v_measure_score:

>>> metrics.v_measure_score(labels_true, labels_pred)
0.516

Формула этой функции следующая:

\[v = \frac{(1 + \beta) \times \text{homogeneity} \times \text{completeness}}{(\beta \times \text{homogeneity} + \text{completeness})}\]

beta по умолчанию имеет значение 1.0, но для использования значения меньше 1 для beta:

>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.547

больший вес будет приписан однородности, а использование значения больше 1:

>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48

больший вес будет приписан полноте.

Мера V фактически эквивалентна взаимной информации (NMI), обсуждаемой выше, с функцией агрегации в виде среднего арифметического [B2011].

Однородность, полноту и V-меру можно вычислить одновременно с помощью homogeneity_completeness_v_measure следующим образом:

>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.67, 0.42, 0.52)

Следующее назначение кластеров немного лучше, поскольку оно однородно, но не полно:

>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68, 0.81)

Примечание

v_measure_score является symmetric: может использоваться для оценки согласие двух независимых назначений на одном и том же наборе данных.

Это не относится к completeness_score и homogeneity_score: оба связаны соотношением:

homogeneity_score(a, b) == completeness_score(b, a)

Преимущества:

• Ограниченные оценки: 0.0 — наихудший результат, 1.0 — идеальный результат.

• Интуитивная интерпретация: кластеризация с плохим V-мерой может быть качественно анализируется с точки зрения однородности и полноты чтобы лучше понять, какие 'типы' ошибок совершаются при назначении.

• Не делается никаких предположений о структуре кластера: может использоваться для сравнения алгоритмов кластеризации, таких как k-means, который предполагает изотропные формы кластеров, с результатами алгоритмов спектральной кластеризации, которые могут находить кластеры с «сложенными» формами.

Недостатки:

• Ранее введенные метрики являются не нормализованы относительно случайной разметки: это означает, что в зависимости от количества образцов, кластеров и истинных классов, полностью случайная маркировка не всегда будет давать одинаковые значения для однородности, полноты и, следовательно, v-меры. В частности случайная маркировка не даст нулевых оценок, особенно когда количество кластеров велико.

  Эту проблему можно безопасно игнорировать, когда количество выборок превышает тысячу, а количество кластеров меньше 10. Для меньших размеров выборки или большего числа кластеров безопаснее использовать скорректированный индекс, такой как Adjusted Rand Index (ARI).

• Эти метрики требуют знания истинных классов в то время как почти никогда не доступны на практике или требуют ручного назначения человеком аннотатором (как в контролируемом обучении).

Примеры

• Коррекция на случайность в оценке производительности кластеризации: Анализ влияния размера набора данных на значение мер кластеризации для случайных назначений.

Математическая формулировка

Оценки однородности и полноты формально задаются как:

\[h = 1 - \frac{H(C|K)}{H(C)}\]

\[c = 1 - \frac{H(K|C)}{H(K)}\]

где \(H(C|K)\) является условная энтропия классов при заданных назначениях кластеров и задается формулой:

\[H(C|K) = - \sum_{c=1}^{|C|} \sum_{k=1}^{|K|} \frac{n_{c,k}}{n} \cdot \log\left(\frac{n_{c,k}}{n_k}\right)\]

и \(H(C)\) является энтропия классов и задается формулой:

\[H(C) = - \sum_{c=1}^{|C|} \frac{n_c}{n} \cdot \log\left(\frac{n_c}{n}\right)\]

с \(n\) общее количество образцов, \(n_c\) и \(n_k\) количество образцов, принадлежащих классу \(c\) и кластер \(k\), и, наконец, \(n_{c,k}\) количество образцов из класса \(c\) назначен кластеру \(k\).

The условная энтропия кластеров при заданном классе \(H(K|C)\) и энтропия кластеров \(H(K)\) определены симметричным образом.

Розенберг и Хиршберг дополнительно определяют V-мера как среднее гармоническое однородности и полноты:

\[v = 2 \cdot \frac{h \cdot c}{h + c}\]

Ссылки

• V-мера: внешняя метрика оценки кластеризации на основе условной энтропии Эндрю Розенберг и Джулия Хиршберг, 2007

[B2011]

Identification and Characterization of Events in Social Media, Хила Беккер, докторская диссертация.

2.3.11.4. Оценки Fowlkes-Mallows

Эти изображения показывают, как схожие признаки объединяются с помощью агломерации признаков. sklearn.metrics.fowlkes_mallows_score) может использоваться когда известны истинные назначения классов образцов. FMI определяется как среднее геометрическое попарной точности и полноты:

\[\text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}}\]

В приведенной выше формуле:

• TP (Истинно положительный): Количество пар точек, которые сгруппированы вместе как в истинных метках, так и в предсказанных метках.

• FP (Ложноположительный): Количество пар точек, которые сгруппированы вместе в предсказанных метках, но не в истинных метках.

• FN (Ложноотрицательный): Количество пар точек, которые сгруппированы вместе в истинных метках, но не в предсказанных метках.

Оценка варьируется от 0 до 1. Высокое значение указывает на хорошее сходство между двумя кластерами.

>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

Можно переставить 0 и 1 в предсказанных метках, переименовать 2 в 3 и получить тот же результат:

>>> labels_pred = [1, 1, 0, 0, 3, 3]

>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140

Идеальная разметка оценивается в 1.0:

>>> labels_pred = labels_true[:]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
1.0

Плохие (например, независимые разметки) имеют нулевые оценки:

>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0

Преимущества:

• Случайные (равномерные) назначения меток имеют оценку FMI, близкую к 0.0 для любого значения n_clusters и n_samples (что не относится к сырой взаимной информации или V-мере, например).

• Верхняя граница 1: Значения, близкие к нулю, указывают на два назначения меток, которые в основном независимы, в то время как значения, близкие к единице, указывают на значительное согласие. Кроме того, значения ровно 0 указывают на чисто независимые назначения меток и FMI ровно 1 указывает, что два назначения меток равны (с перестановкой или без).

• Не делается никаких предположений о структуре кластера: может использоваться для сравнения алгоритмов кластеризации, таких как k-means, который предполагает изотропные формы кластеров, с результатами алгоритмов спектральной кластеризации, которые могут находить кластеры с «сложенными» формами.

Недостатки:

• В отличие от инерции, Меры на основе FMI требуют знания истинных классов хотя на практике почти никогда не доступно или требует ручного назначения человеком-аннотатором (как в настройке обучения с учителем).

Ссылки

• E. B. Fowkles и C. L. Mallows, 1983. "Метод сравнения двух иерархических кластеризаций". Journal of the American Statistical Association. https://www.tandfonline.com/doi/abs/10.1080/01621459.1983.10478008

• Запись в Википедии для индекса Фоулкса-Мэллоуза

2.3.11.5. Коэффициент силуэта

Если истинные метки неизвестны, оценка должна проводиться с использованием самой модели. Коэффициент силуэта (sklearn.metrics.silhouette_score) является примером такой оценки, где более высокий коэффициент силуэта соответствует модели с более четко определенными кластерами. Коэффициент силуэта определяется для каждого образца и состоит из двух оценок:

• a: Среднее расстояние между образцом и всеми другими точками в том же классе.

• b: Среднее расстояние между образцом и всеми другими точками в следующий ближайший кластер.

Коэффициент силуэта s для одного образца тогда задаётся как:

\[s = \frac{b - a}{max(a, b)}\]

Коэффициент силуэта для набора образцов вычисляется как среднее значение коэффициента силуэта для каждого образца.

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

В обычном использовании коэффициент силуэта применяется к результатам кластерного анализа.

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55

Преимущества:

• Оценка ограничена между -1 для некорректной кластеризации и +1 для плотной кластеризации. Оценки около нуля указывают на перекрывающиеся кластеры.

• Оценка выше, когда кластеры плотные и хорошо разделены, что соответствует стандартному понятию кластера.

Недостатки:

• Коэффициент силуэта обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, полученные через DBSCAN.

Примеры

• Выбор количества кластеров с помощью анализа силуэта для кластеризации KMeans : В этом примере анализ силуэта используется для выбора оптимального значения для n_clusters.

Ссылки

• Peter J. Rousseeuw (1987). “Силуэты: графическое средство для интерпретации и проверки кластерного анализа”. Вычислительная и прикладная математика 20: 53-65.

2.3.11.6. Индекс Калинского-Харабаша

Если истинные метки неизвестны, индекс Калински-Харабаша (sklearn.metrics.calinski_harabasz_score) - также известный как критерий отношения дисперсий - может использоваться для оценки модели, где более высокий показатель Калинского-Харабаза соответствует модели с более четко определенными кластерами.

Индекс представляет собой отношение суммы дисперсии между кластерами и дисперсии внутри кластеров для всех кластеров (где дисперсия определяется как сумма квадратов расстояний):

>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)

При обычном использовании индекс Калински-Харабаса применяется к результатам кластерного анализа:

>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.59

Преимущества:

• Оценка выше, когда кластеры плотные и хорошо разделены, что соответствует стандартному понятию кластера.

• Оценка быстро вычисляется.

Недостатки:

• Индекс Калинского-Харабаса обычно выше для выпуклых кластеров, чем для других концепций кластеров, таких как кластеры на основе плотности, полученные через DBSCAN.

Математическая формулировка

Для набора данных \(E\) размера \(n_E\) который был сгруппирован в \(k\) кластеров, оценка Калински-Харабаша \(s\) определяется как отношение среднего межкластерного рассеяния к внутрикластерному рассеянию:

\[s = \frac{\mathrm{tr}(B_k)}{\mathrm{tr}(W_k)} \times \frac{n_E - k}{k - 1}\]

где \(\mathrm{tr}(B_k)\) является следом матрицы дисперсии между группами и \(\mathrm{tr}(W_k)\) является следом матрицы дисперсии внутри кластера, определенной как:

\[W_k = \sum_{q=1}^k \sum_{x \in C_q} (x - c_q) (x - c_q)^T\]

\[B_k = \sum_{q=1}^k n_q (c_q - c_E) (c_q - c_E)^T\]

с \(C_q\) множество точек в кластере \(q\), \(c_q\) центр кластера \(q\), \(c_E\) центр \(E\), и \(n_q\) количество точек в кластере \(q\).

Ссылки

• Caliński, T., & Harabasz, J. (1974). “Дендритный метод для кластерного анализа”. Communications in Statistics-theory and Methods 3: 1-27.

2.3.11.7. Индекс Дэвиса-Боулдина

Если истинные метки неизвестны, индекс Дэвиса-Боулдина (sklearn.metrics.davies_bouldin_score) может использоваться для оценки модели, где более низкий индекс Дэвиса-Боулдина соответствует модели с лучшим разделением между кластерами.

Этот индекс означает среднее 'сходство' между кластерами, где сходство — это мера, сравнивающая расстояние между кластерами с размером самих кластеров.

Ноль — наименьший возможный балл. Значения ближе к нулю указывают на лучшее разделение.

При обычном использовании индекс Дэвиса-Боулдина применяется к результатам кластерного анализа следующим образом:

>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> from sklearn.cluster import KMeans
>>> from sklearn.metrics import davies_bouldin_score
>>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans.labels_
>>> davies_bouldin_score(X, labels)
0.666

Преимущества:

• Вычисление Davies-Bouldin проще, чем вычисление оценок силуэта.

• Индекс основан исключительно на количествах и признаках, присущих набору данных, так как его вычисление использует только попарные расстояния.

Недостатки:

• Индекс Дэвиса-Боулдина обычно выше для выпуклых кластеров, чем для других концепций кластеризации, таких как кластеры на основе плотности, полученные, например, с помощью DBSCAN.

• Использование расстояния до центроида ограничивает метрику расстояния евклидовым пространством.

Математическая формулировка

Индекс определяется как среднее сходство между каждым кластером \(C_i\) для \(i=1, ..., k\) и его наиболее похожий \(C_j\). В контексте этого индекса сходство определяется как мера \(R_{ij}\) который компромиссно учитывает:

• \(s_i\), среднее расстояние между каждой точкой кластера \(i\) и центроид этого кластера — также известный как диаметр кластера.

• \(d_{ij}\), расстояние между центроидами кластеров \(i\) и \(j\).

Простой выбор для построения \(R_{ij}\) так, чтобы она была неотрицательной и симметричной:

\[R_{ij} = \frac{s_i + s_j}{d_{ij}}\]

Тогда индекс Дэвиса-Боулдина определяется как:

\[DB = \frac{1}{k} \sum_{i=1}^k \max_{i \neq j} R_{ij}\]

Ссылки

• Дэвис, Дэвид Л.; Боулдин, Дональд В. (1979). "A Cluster Separation Measure" IEEE Transactions on Pattern Analysis and Machine Intelligence. PAMI-1 (2): 224-227.

• Халкиди, Мария; Батистикис, Яннис; Вазиргианнис, Михалис (2001). «О методах проверки кластеризации» Journal of Intelligent Information Systems, 17(2-3), 107-145.

• Статья в Википедии об индексе Дэвиса-Боулдина.

2.3.11.8. Матрица сопряженности

Матрица сопряженности (sklearn.metrics.cluster.contingency_matrix) сообщает мощность пересечения для каждой пары истинный/предсказанный кластер. Матрица сопряженности предоставляет достаточную статистику для всех метрик кластеризации, где выборки независимы и одинаково распределены, и не требуется учитывать некоторые экземпляры, не попавшие в кластеры.

Вот пример:

>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
       [0, 1, 2]])

Первая строка выходного массива показывает, что есть три образца, чей истинный кластер — "a". Из них два находятся в предсказанном кластере 0, один — в 1, и ни одного — в 2. А вторая строка показывает, что есть три образца, чей истинный кластер — "b". Из них ни одного в предсказанном кластере 0, один — в 1 и два — в 2.

A матрица ошибок для классификации представляет собой квадратную таблицу сопряженности, где порядок строк и столбцов соответствует списку классов.

Преимущества:

• Позволяет изучить распределение каждого истинного кластера по предсказанным кластерам и наоборот.

• Рассчитанная таблица сопряженности обычно используется при вычислении статистики сходства (как другие, перечисленные в этом документе) между двумя кластеризациями.

Недостатки:

• Матрица сопряженности легко интерпретируется для небольшого числа кластеров, но становится очень сложной для интерпретации при большом числе кластеров.

• Он не дает единой метрики для использования в качестве цели оптимизации кластеризации.

Ссылки

• Статья в Википедии о матрице сопряженности

2.3.11.9. Матрица путаницы пар

Матрица парной путаницы (sklearn.metrics.cluster.pair_confusion_matrix) является матрицей сходства 2x2

\[\begin{split}C = \left[\begin{matrix} C_{00} & C_{01} \\ C_{10} & C_{11} \end{matrix}\right]\end{split}\]

между двумя кластеризациями, вычисленными путем рассмотрения всех пар образцов и подсчета пар, которые назначены в одни и те же или разные кластеры при истинной и предсказанной кластеризациях.

Он имеет следующие записи:

\(C_{00}\) : количество пар, в которых обе кластеризации имеют образцы, не сгруппированные вместе

\(C_{10}\) : количество пар, где истинная кластеризация меток имеет образцы, сгруппированные вместе, но другая кластеризация не имеет образцы, сгруппированные вместе

\(C_{01}\) : количество пар, где истинная метка кластеризации не имеет образцы, сгруппированные вместе, но другая кластеризация имеет образцы, сгруппированные вместе

\(C_{11}\) : количество пар, в которых обе кластеризации имеют образцы, сгруппированные вместе

Рассматривая пару выборок, которые сгруппированы вместе как положительная пара, тогда, как в бинарной классификации, количество истинных отрицаний равно \(C_{00}\), ложноотрицательные значения это \(C_{10}\), истинные положительные результаты — это \(C_{11}\) и ложные срабатывания - это \(C_{01}\).

Идеально совпадающие метки имеют все ненулевые элементы на диагонали независимо от фактических значений меток:

>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
       [0, 4]])

>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
       [0, 4]])

Разметки, которые назначают все элементы классов одним и тем же кластерам, являются полными, но не всегда чистыми, поэтому штрафуются и имеют некоторые ненулевые элементы вне диагонали:

>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
       [0, 2]])

Матрица не является симметричной:

>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
       [2, 2]])

Если члены классов полностью разделены по разным кластерам, назначение полностью неполное, поэтому матрица имеет все нулевые диагональные элементы:

>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0,  0],
       [12,  0]])

Ссылки

• “Сравнение разделений” L. Hubert и P. Arabie, Journal of Classification 1985