1.2. Линейный и квадратичный дискриминантный анализ#
Линейный дискриминантный анализ
(LinearDiscriminantAnalysis) и квадратичный дискриминантный анализ
(QuadraticDiscriminantAnalysis) — два классических
классификатора, которые, как следует из их названий, имеют линейную и квадратичную решающие
поверхности соответственно.
Эти классификаторы привлекательны, поскольку имеют аналитические решения, которые можно легко вычислить, по своей природе являются многоклассовыми, доказали свою эффективность на практике и не требуют настройки гиперпараметров.
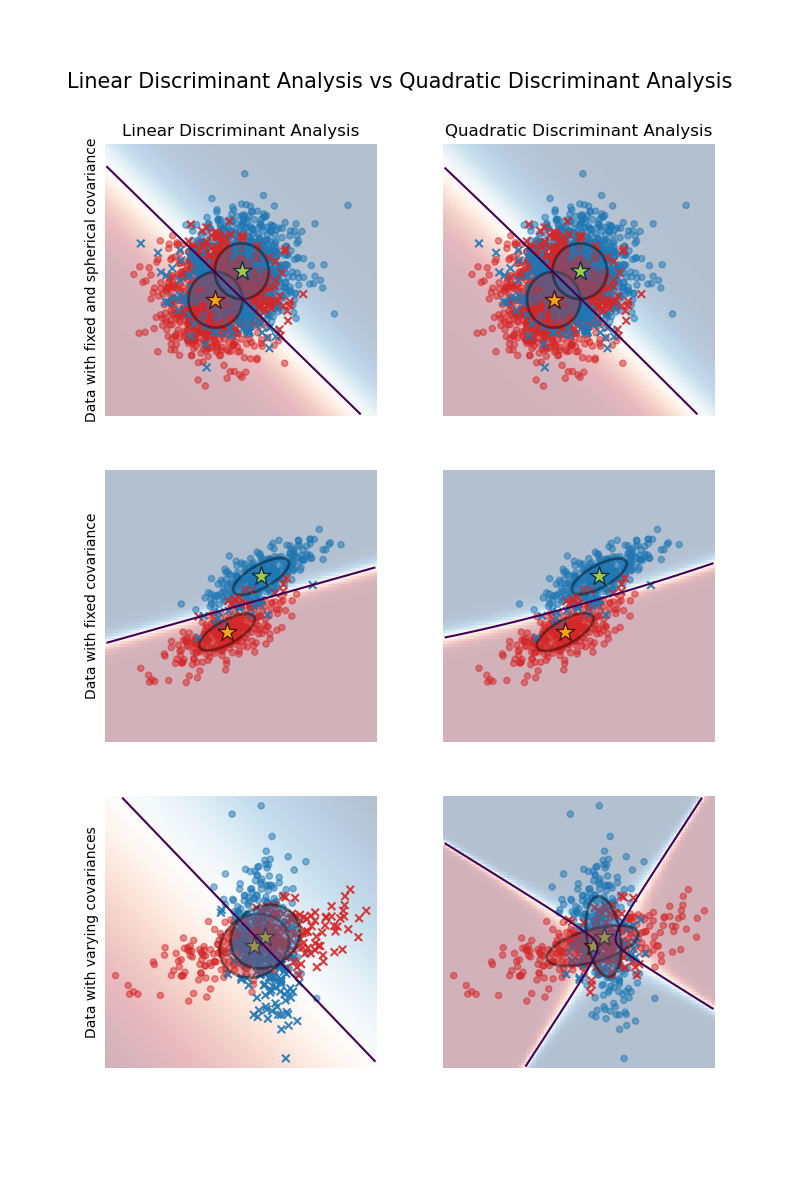
График показывает границы решений для линейного дискриминантного анализа и квадратичного дискриминантного анализа. Нижний ряд демонстрирует, что линейный дискриминантный анализ может изучать только линейные границы, в то время как квадратичный дискриминантный анализ может изучать квадратичные границы и поэтому является более гибким.
Примеры
Линейный и квадратичный дискриминантный анализ с эллипсоидом ковариации: Сравнение LDA и QDA на синтетических данных.
1.2.1. Снижение размерности с использованием линейного дискриминантного анализа#
LinearDiscriminantAnalysis может использоваться для выполнения контролируемого понижения размерности путем проецирования входных данных на линейное подпространство, состоящее из направлений, которые максимизируют разделение между классами (в точном смысле, обсуждаемом в разделе математики ниже). Размерность выхода обязательно меньше количества классов, поэтому это, как правило, довольно сильное понижение размерности и имеет смысл только в многоклассовой настройке.
Это реализовано в transform методу. Желаемую размерность можно
задать с помощью n_components параметр. Этот параметр не влияет на fit и predict методы.
Примеры
Сравнение LDA и PCA 2D проекции набора данных Iris: Сравнение LDA и PCA для уменьшения размерности набора данных Iris
1.2.2. Математическая формулировка классификаторов LDA и QDA#
Как LDA, так и QDA могут быть выведены из простых вероятностных моделей, которые моделируют условное распределение данных по классам \(P(X|y=k)\) для каждого класса \(k\). Затем прогнозы можно получить, используя правило Байеса, для каждого обучающего образца \(x \in \mathbb{R}^d\):
и мы выбираем класс \(k\) который максимизирует эту апостериорную вероятность.
Более конкретно, для линейного и квадратичного дискриминантного анализа, \(P(x|y)\) моделируется как многомерное гауссовское распределение с плотностью:
где \(d\) это количество признаков.
1.2.2.1. QDA#
Согласно приведенной выше модели, логарифм апостериорной вероятности равен:
где постоянный член \(Cst\) соответствует знаменателю \(P(x)\), в дополнение к другим постоянным членам из гауссовского распределения. Предсказанный класс - это тот, который максимизирует этот логарифм апостериорной вероятности.
Примечание
Связь с гауссовским наивным байесовским классификатором
Если в модели QDA предполагается, что ковариационные матрицы диагональны, то входные данные считаются условно независимыми в каждом классе, и результирующий классификатор эквивалентен наивному байесовскому классификатору Гаусса naive_bayes.GaussianNB.
1.2.2.2. LDA#
LDA является частным случаем QDA, где предполагается, что гауссовы распределения для каждого класса имеют одну и ту же ковариационную матрицу: \(\Sigma_k = \Sigma\) для всех \(k\). Это сводит логарифмическую апостериорную вероятность к:
Термин \((x-\mu_k)^T \Sigma^{-1} (x-\mu_k)\) соответствует Расстояние Махаланобиса между выборкой \(x\) и среднее \(\mu_k\). Расстояние Махаланобиса показывает, насколько близко \(x\) от \(\mu_k\), а также учитывая дисперсию каждого признака. Таким образом, мы можем интерпретировать LDA как назначение \(x\) к классу, чье среднее значение является ближайшим с точки зрения расстояния Махаланобиса, также учитывая априорные вероятности классов.
Логарифм апостериорной вероятности LDA также может быть записан [3] как:
где \(\omega_k = \Sigma^{-1} \mu_k\) и \(\omega_{k0} =
-\frac{1}{2} \mu_k^T\Sigma^{-1}\mu_k + \log P (y = k)\). Эти величины
соответствуют coef_ и intercept_ атрибуты, соответственно.
Из приведённой выше формулы ясно, что LDA имеет линейную решающую поверхность. В случае QDA нет предположений о ковариационных матрицах \(\Sigma_k\) гауссовых распределений, приводя к квадратичным поверхностям решений. См. [1] для получения дополнительной информации.
1.2.3. Математическая формулировка уменьшения размерности LDA#
Сначала обратите внимание, что K-средних \(\mu_k\) являются векторами в \(\mathbb{R}^d\), и они лежат в аффинном подпространстве \(H\) размерности не более \(K - 1\) (2 точки лежат на линии, 3 точки лежат на плоскости и т.д.).
Как упоминалось выше, мы можем интерпретировать LDA как присваивание \(x\) к классу, среднее значение которого \(\mu_k\) является ближайшим с точки зрения расстояния Махаланобиса, а также учитывает априорные вероятности классов. Альтернативно, LDA эквивалентна сначала сферирование данные так, чтобы ковариационная матрица была единичной, а затем присвоение \(x\) к ближайшему среднему в терминах евклидова расстояния (с учётом априорных вероятностей классов).
Вычисление евклидовых расстояний в этом d-мерном пространстве эквивалентно сначала проецированию точек данных в \(H\), и вычисление расстояний там (поскольку другие размерности будут одинаково вносить вклад в каждый класс с точки зрения расстояния). Другими словами, если \(x\) наиболее близок к \(\mu_k\) в исходном пространстве, это также будет иметь место в \(H\). Это показывает, что неявно в классификаторе LDA происходит уменьшение размерности путем линейной проекции на \(K-1\) -мерном пространстве.
Мы можем уменьшить размерность ещё больше, до выбранного \(L\), путём проецирования на линейное подпространство \(H_L\) который максимизирует дисперсию
\(\mu^*_k\) после проекции (по сути, мы выполняем форму PCA для преобразованных средних классов \(\mu^*_k\)). Это \(L\) соответствует
n_components параметр, используемый в
transform метод. См.
[1] для получения дополнительной информации.
1.2.4. Оценщик сжатия и ковариации#
Сжатие — это форма регуляризации, используемая для улучшения оценки ковариационных матриц в ситуациях, когда количество обучающих выборок мало по сравнению с количеством признаков. В этом сценарии эмпирическая выборочная ковариация является плохим оценщиком, и сжатие помогает улучшить обобщающую способность классификатора. Сжатие можно использовать с LDA (или QDA), установив shrinkage параметр
LinearDiscriminantAnalysis класс
(или QuadraticDiscriminantAnalysis) в 'auto'.
Это автоматически определяет оптимальный параметр сжатия аналитическим
способом, следуя лемме, представленной Ледойтом и Вольфом [2]. Обратите внимание, что
в настоящее время сжатие работает только при установке solver параметр для 'lsqr'
или 'eigen' (только 'eigen' реализован для QDA).
The shrinkage параметр также может быть установлен вручную между 0 и 1. В частности, значение 0 соответствует отсутствию сжатия (что означает, что будет использоваться эмпирическая ковариационная матрица), а значение 1 соответствует полному сжатию (что означает, что диагональная матрица дисперсий будет использоваться в качестве оценки ковариационной матрицы). Установка этого параметра в значение между этими двумя крайностями позволит оценить сжатую версию ковариационной матрицы.
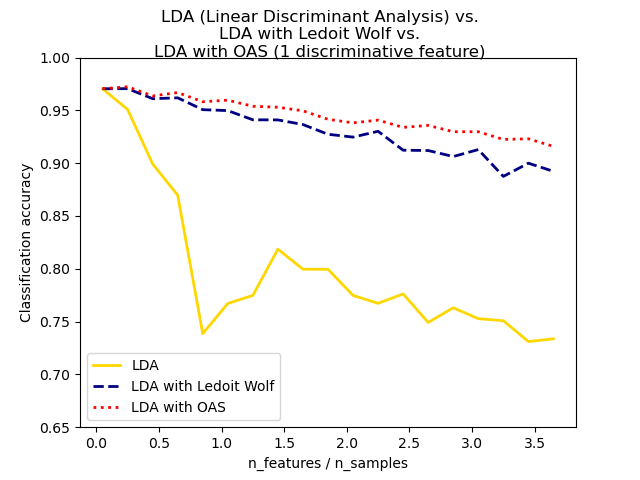
Сжатый оценщик ковариации Ледойта и Вольфа не всегда может быть лучшим выбором. Например, если распределение данных является нормальным, оценщик Oracle Approximating Shrinkage sklearn.covariance.OAS
дает меньшую среднеквадратичную ошибку, чем та, что получена по формуле Ледойта и Вольфа,
используемой с shrinkage="auto". В LDA и QDA данные предполагаются гауссовыми
условно по классу. Если эти предположения выполняются, использование LDA и QDA с
оценщиком ковариации OAS даст лучшую точность
классификации, чем если используется оценщик Ledoit и Wolf или эмпирический оценщик ковариации.
Оценщик ковариации может быть выбран с помощью covariance_estimator
параметр discriminant_analysis.LinearDiscriminantAnalysis
и discriminant_analysis.QuadraticDiscriminantAnalysis классов. Оценщик ковариации должен иметь fit метод и
covariance_ атрибут, как и все ковариационные оценщики в
sklearn.covariance модуль.
Примеры
Нормальный, Ledoit-Wolf и OAS линейный дискриминантный анализ для классификации: Сравнение классификаторов LDA с эмпирической оценкой ковариации, оценкой Ледойта-Вольфа и оценкой OAS.
1.2.5. Алгоритмы оценки#
Использование LDA и QDA требует вычисления логарифма апостериорной вероятности, который зависит от априорных вероятностей классов. Это выполняется для каждого признака итеративно, а затем повторяется для \(P(y=k)\), средние значения классов \(\mu_k\), и ковариационные матрицы.
Решатель 'svd' является решателем по умолчанию для
LinearDiscriminantAnalysis и
QuadraticDiscriminantAnalysis.
Он может выполнять как классификацию, так и преобразование (для LDA).
Поскольку он не полагается на вычисление ковариационной матрицы, решатель 'svd'
может быть предпочтительнее в ситуациях, когда количество признаков велико.
Решатель 'svd' нельзя использовать с shrinkage.
Для QDA использование решателя SVD основано на том, что ковариационная матрица \(\Sigma_k\) обучается на преобразованном выходе, т.е. используя только релевантные признаки. Вы можете выполнять аналогичные операции с другими методами отбора признаков, а также с классификаторами, которые предоставляют способ оценки важности признаков. См. \(\frac{1}{n - 1}
X_k^TX_k = \frac{1}{n - 1} V S^2 V^T\) где \(V\) происходит из SVD (центрированной)
матрицы: \(X_k = U S V^T\). Оказывается, мы можем вычислить
логарифм апостериорной вероятности выше без явного вычисления \(\Sigma\):
вычисление \(S\) и \(V\) через SVD \(X\) достаточно. Для LDA вычисляются два SVD: SVD центрированной входной матрицы \(X\)
и SVD векторов средних значений по классам.
The 'lsqr' solver — эффективный алгоритм, который работает только для классификации. Ему необходимо явно вычислять ковариационную матрицу
\(\Sigma\)и поддерживает сжатие и пользовательские оценки ковариации.
Этот решатель вычисляет коэффициенты
\(\omega_k = \Sigma^{-1}\mu_k\) путем решения для \(\Sigma \omega =
\mu_k\), тем самым избегая явного вычисления обратной матрицы
\(\Sigma^{-1}\).
The 'eigen' решатель для LinearDiscriminantAnalysis
основан на оптимизации отношения межклассового разброса к внутриклассовому разбросу. Может использоваться как для классификации, так и для преобразования, и поддерживает сжатие.
Для QuadraticDiscriminantAnalysis, 'eigen' решатель основан на вычислении собственных значений и собственных векторов каждой ковариационной матрицы класса. Он позволяет использовать сжатие для классификации. Однако, 'eigen' решателю необходимо вычислить ковариационную матрицу, поэтому он может не подходить для ситуаций с большим количеством признаков.
Ссылки