1.10. Деревья решений#

Деревья решений (DTs) являются непараметрическим методом обучения с учителем, используемым для классификация и регрессия. Цель состоит в создании модели, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из признаков данных. Дерево можно рассматривать как кусочно-постоянную аппроксимацию.

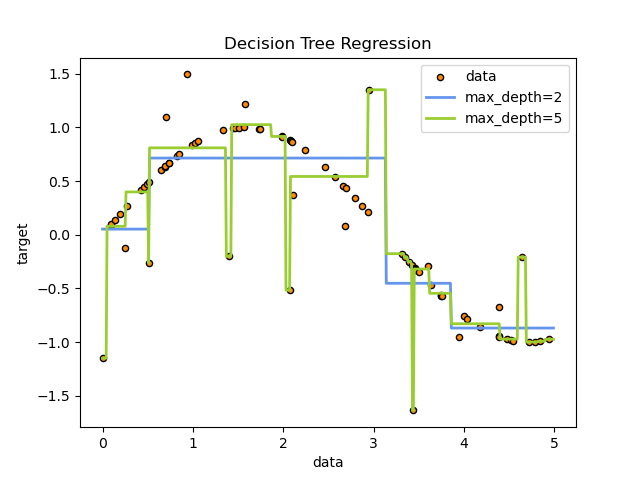
Например, в приведенном ниже примере деревья решений обучаются на данных, чтобы аппроксимировать синусоидальную кривую с помощью набора правил решений "если-то-иначе". Чем глубже дерево, тем сложнее правила решений и лучше модель.

../_images/sphx_glr_plot_tree_regression_001.png

Некоторые преимущества деревьев решений:

  • Просто для понимания и интерпретации. Деревья можно визуализировать.

  • Требует минимальной подготовки данных. Другие методы часто требуют нормализации данных, создания фиктивных переменных и удаления пустых значений. Некоторые комбинации деревьев и алгоритмов поддерживают пропущенные значения.

  • Стоимость использования дерева (т.е., предсказания данных) логарифмическая по количеству точек данных, использованных для обучения дерева.

  • Может обрабатывать как числовые, так и категориальные данные. Однако текущая реализация scikit-learn не поддерживает категориальные переменные. Другие методы обычно специализируются на анализе наборов данных, содержащих только один тип переменных. См. алгоритмы для получения дополнительной информации.

  • Способен обрабатывать многомерные задачи.

  • Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко описывается булевой логикой. В отличие от этого, в модели черного ящика (например, в искусственной нейронной сети) результаты могут быть сложнее для интерпретации.

  • Возможность проверки модели с использованием статистических тестов. Это позволяет учитывать надежность модели.

  • Хорошо работает даже если его предположения несколько нарушены истинной моделью, из которой были сгенерированы данные.

Недостатки деревьев решений включают:

  • Обучающиеся деревья решений могут создавать излишне сложные деревья, которые не хорошо обобщают данные. Это называется переобучением. Механизмы такие как обрезка, установка минимального количества выборок, требуемых в листовом узле или установка максимальной глубины дерева необходимы, чтобы избежать этой проблемы.

  • Деревья решений могут быть нестабильными, потому что небольшие вариации в данных могут привести к генерации совершенно другого дерева. Эта проблема смягчается использованием деревьев решений в составе ансамбля.

  • Прогнозы деревьев решений не являются ни гладкими, ни непрерывными, а представляют собой кусочно-постоянные аппроксимации, как показано на рисунке выше. Поэтому они плохо справляются с экстраполяцией.

  • Проблема обучения оптимальному дереву решений известна как NP-полная при нескольких аспектах оптимальности и даже для простых понятий. Следовательно, практические алгоритмы обучения деревьям решений основаны на эвристических алгоритмах, таких как жадный алгоритм, где локально оптимальные решения принимаются в каждом узле. Такие алгоритмы не могут гарантировать возвращение глобально оптимального дерева решений. Это можно смягчить, обучая несколько деревьев в ансамблевом обучении, где признаки и выборки случайным образом выбираются с возвращением.

  • Существуют концепции, которые сложно изучить, потому что деревья решений не выражают их легко, такие как XOR, четность или задачи мультиплексора.

  • Алгоритмы обучения деревьям решений создают смещенные деревья, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед обучением дерева решений.

1.10.1. Классификация#

DecisionTreeClassifier это класс, способный выполнять многоклассовую классификацию на наборе данных.

Как и с другими классификаторами, DecisionTreeClassifier принимает на вход два массива: массив X, разреженный или плотный, формы (n_samples, n_features) содержащий обучающие выборки, и массив Y целочисленных значений, форма (n_samples,), содержащий метки классов для обучающих выборок:

>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)

После обучения модель может использоваться для предсказания класса образцов:

>>> clf.predict([[2., 2.]])
array([1])

В случае, если есть несколько классов с одинаковой и наивысшей вероятностью, классификатор предскажет класс с наименьшим индексом среди этих классов.

В качестве альтернативы выводу конкретного класса можно предсказывать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе:

>>> clf.predict_proba([[2., 2.]])
array([[0., 1.]])

DecisionTreeClassifier способен как к бинарной (где метки [-1, 1]), так и к многоклассовой (где метки [0, …, K-1]) классификации.

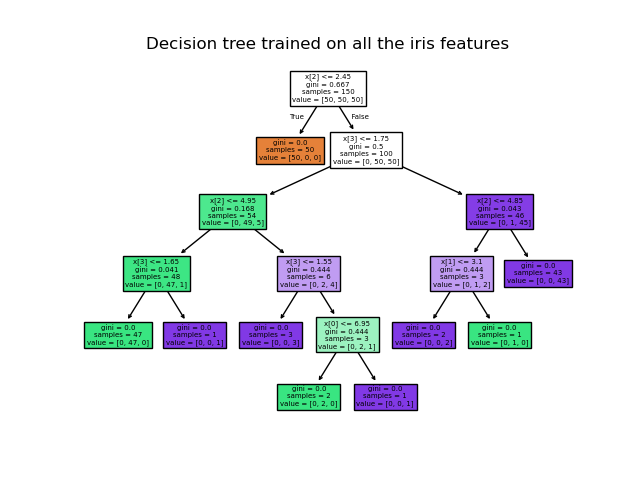
Используя набор данных Iris, мы можем построить дерево следующим образом:

>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)

После обучения вы можете построить дерево с помощью plot_tree функция:

>>> tree.plot_tree(clf)
[...]
../_images/sphx_glr_plot_iris_dtc_002.png
Альтернативные способы экспорта деревьев#

Мы также можем экспортировать дерево в Graphviz формат с использованием export_graphviz экспортёр. Если вы используете conda менеджер пакетов, бинарные файлы graphviz и пакет Python могут быть установлены с помощью conda install python-graphviz.

В качестве альтернативы бинарные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а обертку Python установить из pypi с помощью pip install graphviz.

Ниже приведён пример экспорта graphviz для вышеуказанного дерева, обученного на полном наборе данных iris; результаты сохранены в выходном файле iris.pdf:

>>> import graphviz
>>> dot_data = tree.export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")

The export_graphviz экспортер также поддерживает различные эстетические опции, включая раскраску узлов по их классу (или значению для регрессии) и использование явных имён переменных и классов при желании. Jupyter notebooks также автоматически отображают эти графики встроенными:

>>> dot_data = tree.export_graphviz(clf, out_file=None,
...                      feature_names=iris.feature_names,
...                      class_names=iris.target_names,
...                      filled=True, rounded=True,
...                      special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
../_images/iris.svg
../_images/sphx_glr_plot_iris_dtc_001.png

Кроме того, дерево также может быть экспортировано в текстовом формате с помощью функции export_text. Этот метод не требует установки внешних библиотек и более компактен:

>>> from sklearn.datasets import load_iris
>>> from sklearn.tree import DecisionTreeClassifier
>>> from sklearn.tree import export_text
>>> iris = load_iris()
>>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2)
>>> decision_tree = decision_tree.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=iris['feature_names'])
>>> print(r)
|--- petal width (cm) <= 0.80
|   |--- class: 0
|--- petal width (cm) >  0.80
|   |--- petal width (cm) <= 1.75
|   |   |--- class: 1
|   |--- petal width (cm) >  1.75
|   |   |--- class: 2

Примеры

1.10.2. Регрессия#

../_images/sphx_glr_plot_tree_regression_001.png

Деревья решений также могут применяться к задачам регрессии, используя DecisionTreeRegressor класс.

Как и в случае классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей точкой вместо целочисленных значений:

>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])

Примеры

1.10.3. Многозадачные проблемы#

Многомерная задача — это задача обучения с учителем с несколькими выходными переменными для предсказания, то есть когда Y является двумерным массивом формы (n_samples, n_outputs).

Когда нет корреляции между выходами, очень простой способ решить этот тип проблемы — построить n независимых моделей, т.е. по одной для каждого выхода, а затем использовать эти модели для независимого предсказания каждого из n выходов. Однако, поскольку вероятно, что значения выходов, связанные с одним и тем же входом, сами коррелируют, часто лучшим способом является построение одной модели, способной одновременно предсказывать все n выходов. Во-первых, это требует меньше времени на обучение, поскольку строится только один оценщик. Во-вторых, точность обобщения полученного оценщика часто может быть повышена.

Что касается деревьев решений, эта стратегия может быть легко использована для поддержки многомерных задач. Это требует следующих изменений:

  • Хранить n выходных значений в листьях вместо 1;

  • Используйте критерии разделения, которые вычисляют среднее снижение по всем n выходам.

Этот модуль предлагает поддержку многомерных задач, реализуя эту стратегию как в DecisionTreeClassifier и DecisionTreeRegressor. Если дерево решений обучается на выходном массиве Y формы (n_samples, n_outputs) тогда результирующий оценщик будет:

  • Вывод n_output значений при predict;

  • Вывести список из n_output массивов вероятностей классов при predict_proba.

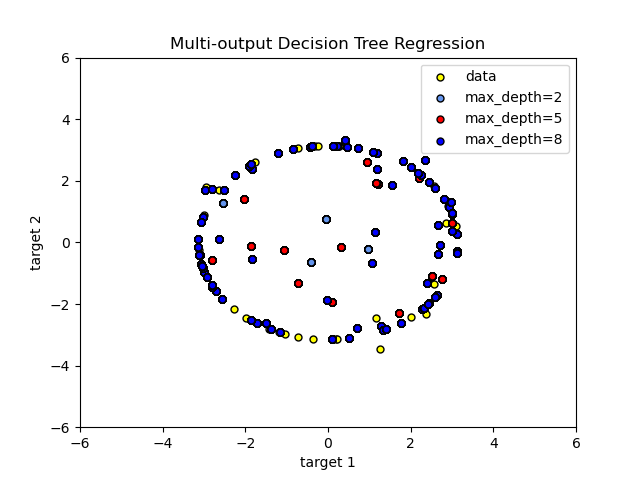
Использование деревьев с множественным выходом для регрессии демонстрируется в Регрессия дерева решений. В этом примере входные данные X представляют собой одно вещественное значение, а выходные данные Y - синус и косинус X.

../_images/sphx_glr_plot_tree_regression_002.png

Использование многоцелевых деревьев для классификации демонстрируется в Завершение лица с помощью многоканальных оценщиков. В этом примере входы X — пиксели верхней половины лиц, а выходы Y — пиксели нижней половины этих лиц.

../_images/sphx_glr_plot_multioutput_face_completion_001.png

Примеры

Ссылки

1.10.4. Сложность#

В следующей таблице показаны оценки сложности в наихудшем случае для сбалансированного бинарного дерева:

Разделитель

Общая стоимость обучения

Общая стоимость вывода

“best”

\(\mathcal{O}(n_{features} \, n^2_{samples} \log(n_{samples}))\)

\(\mathcal{O}(\log(n_{samples}))\)

"random"

\(\mathcal{O}(n_{features} \, n^2_{samples})\)

\(\mathcal{O}(\log(n_{samples}))\)

В общем случае стоимость обучения для построения сбалансированного бинарного дерева на каждом узле является

\[\mathcal{O}(n_{features}n_{samples}\log (n_{samples})) + \mathcal{O}(n_{features}n_{samples})\]

Первый член — это стоимость сортировки \(n_{samples}\) повторяется для \(n_{features}\). Второй член — это линейный просмотр кандидатных точек разделения, чтобы найти признак, который предлагает наибольшее снижение критерия нечистоты. Последний является второстепенным для жадной стратегии разделителя «best» и поэтому обычно отбрасывается.

Независимо от стратегии разделения, после суммирования стоимости по все внутренние узлы, общая сложность масштабируется линейно с \(n_{nodes}=n_{leaves}-1\), что является \(\mathcal{O}(n_{samples})\) в наихудшей сложности, то есть когда дерево растет до тех пор, пока каждый образец не окажется в своем собственном листе.

Многие реализации, такие как scikit-learn, используют эффективные приемы кэширования для отслеживания общего порядка индексов в каждом узле, чтобы признаки не нужно было пересортировывать на каждом узле; следовательно, временная сложность этих реализаций составляет всего \(\mathcal{O}(n_{features}n_{samples}\log(n_{samples}))\) [1].

#24264 \(\mathcal{O}(\text{depth})\)В приблизительно сбалансированном двоичном дереве каждое разделение делит данные пополам, и количество таких делений растет с глубиной как степени двойки. Если этот процесс продолжается до тех пор, пока каждый образец не окажется изолированным в своем собственном листе, результирующая глубина равна \(\mathcal{O}(\log(n_{samples}))\).

Ссылки

1.10.5. Советы по практическому использованию#

  • Деревья решений склонны к переобучению на данных с большим количеством признаков. Получение правильного соотношения количества выборок к количеству признаков важно, поскольку дерево с малым количеством выборок в многомерном пространстве с высокой вероятностью переобучится.

  • Рассмотрите выполнение снижения размерности (PCA, ICA, или Выбор признаков) заранее, чтобы дать вашему дереву больше шансов найти дискриминативные признаки.

  • Понимание структуры дерева решений поможет получить больше информации о том, как дерево решений делает прогнозы, что важно для понимания значимых признаков в данных.

  • Визуализируйте своё дерево во время обучения с помощью export функция. Используйте max_depth=3 как начальная глубина дерева, чтобы почувствовать, как дерево подгоняется к вашим данным, а затем увеличить глубину.

  • Помните, что количество образцов, необходимых для заполнения дерева, удваивается с каждым дополнительным уровнем роста дерева. Используйте max_depth для контроля размера дерева, чтобы предотвратить переобучение.

  • Используйте min_samples_split или min_samples_leaf чтобы гарантировать, что несколько образцов информируют каждое решение в дереве, контролируя, какие разбиения будут рассматриваться. Очень маленькое число обычно означает, что дерево переобучится, тогда как большое число помешает дереву обучаться на данных. Попробуйте min_samples_leaf=5 в качестве начального значения. Если размер выборки сильно варьируется, можно использовать число с плавающей точкой в процентах для этих двух параметров. Хотя min_samples_split может создавать сколь угодно маленькие листья, min_samples_leaf гарантирует, что каждый лист имеет минимальный размер, избегая листов с низкой дисперсией и переобучением в задачах регрессии. Для классификации с небольшим количеством классов, min_samples_leaf=1 часто является лучшим выбором.

    Обратите внимание, что min_samples_split рассматривает образцы напрямую и независимо от sample_weight, если предоставлено (например, узел с m взвешенными выборками все равно рассматривается как имеющий ровно m выборок). Рассмотрите min_weight_fraction_leaf или min_impurity_decrease если требуется учет весов выборок при разбиениях.

  • Сбалансируйте ваш набор данных перед обучением, чтобы предотвратить смещение дерева в сторону доминирующих классов. Балансировка классов может быть выполнена путём выборки равного количества образцов из каждого класса или, предпочтительно, путём нормализации суммы весов образцов (sample_weight) для каждого класса в одно и то же значение. Также обратите внимание, что критерии предварительной обрезки на основе веса, такие как min_weight_fraction_leaf, тогда будет менее смещенным в сторону доминирующих классов, чем критерии, которые не учитывают веса выборок, такие как min_samples_leaf.

  • Если выборки взвешены, будет проще оптимизировать структуру дерева с использованием критерия предварительной обрезки на основе весов, такого как min_weight_fraction_leaf, что гарантирует, что листовые узлы содержат как минимум долю от общей суммы весов образцов.

  • Все деревья решений используют np.float32 массивы внутри. Если обучающие данные не в этом формате, будет создана копия набора данных.

  • Если входная матрица X очень разрежена, рекомендуется преобразовать в разреженный csc_matrix перед вызовом fit и sparse csr_matrix перед вызовом predict. Время обучения может быть на порядки быстрее для разреженной матрицы по сравнению с плотной матрицей, когда признаки имеют нулевые значения в большинстве выборок.

1.10.6. Алгоритмы деревьев: ID3, C4.5, C5.0 и CART#

Каковы все различные алгоритмы деревьев решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?

Различные алгоритмы деревьев решений#

ID3 (Iterative Dichotomiser 3) был разработан в 1986 году Россом Квинланом. Алгоритм создаёт многостороннее дерево, находя для каждого узла (т.е. жадным способом) категориальный признак, который даст наибольший прирост информации для категориальных целей. Деревья растут до максимального размера, а затем обычно применяется этап обрезки для улучшения способности дерева обобщать на невидимые данные.

C4.5 является преемником ID3 и устраняет ограничение, согласно которому признаки должны быть категориальными, динамически определяя дискретный атрибут (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т.е. результат алгоритма ID3) в наборы правил if-then. Затем точность каждого правила оценивается, чтобы определить порядок их применения. Обрезка выполняется путем удаления предварительного условия правила, если точность правила улучшается без него.

C5.0 — последняя версия Квинлана, выпущенная под проприетарной лицензией. Она использует меньше памяти и строит меньшие наборы правил, чем C4.5, будучи более точной.

CART (Classification and Regression Trees) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессия) и не вычисляет наборы правил. CART строит бинарные деревья, используя признаки и пороги, которые дают наибольший прирост информации на каждом узле.

scikit-learn использует оптимизированную версию алгоритма CART; однако, реализация scikit-learn пока не поддерживает категориальные переменные.

1.10.7. Математическая формулировка#

Для заданных обучающих векторов \(x_i \in R^n\), i=1,…, l и вектор меток \(y \in R^l\), дерево решений рекурсивно разделяет пространство признаков таким образом, что образцы с одинаковыми метками или схожими целевыми значениями группируются вместе.

Пусть данные в узле \(m\) может быть представлен \(Q_m\) с \(n_m\) выборок. Для каждого кандидата на разделение \(\theta = (j, t_m)\) состоящий из признака \(j\) и порог \(t_m\), разделить данные на \(Q_m^{left}(\theta)\) и \(Q_m^{right}(\theta)\) подмножества

\[ \begin{align}\begin{aligned}Q_m^{left}(\theta) = \{(x, y) | x_j \leq t_m\}\\Q_m^{right}(\theta) = Q_m \setminus Q_m^{left}(\theta)\end{aligned}\end{align} \]

Качество кандидата на разделение узла \(m\) затем вычисляется с использованием функции неопределенности или функции потерь \(H()\), выбор которого зависит от решаемой задачи (классификация или регрессия)

\[G(Q_m, \theta) = \frac{n_m^{left}}{n_m} H(Q_m^{left}(\theta)) + \frac{n_m^{right}}{n_m} H(Q_m^{right}(\theta))\]

Выбрать параметры, которые минимизируют неопределённость

\[\theta^* = \operatorname{argmin}_\theta G(Q_m, \theta)\]

Стратегия выбора разделения в каждом узле контролируется splitter параметр:

  • С лучший разделитель (по умолчанию, splitter='best'), \(\theta^*\) находится путем выполнения жадный исчерпывающий поиск по всем доступным признакам и всем возможным порогам \(t_m\) (т.е. средние точки между отсортированными, различными значениями признаков), выбирая пару, которая точно минимизирует \(G(Q_m, \theta)\).

  • С случайный разделитель (splitter='random'), \(\theta^*\) находится путем выборки один случайный порог кандидата для каждой доступной признака. Это выполняет стохастическую аппроксимацию жадного поиска, эффективно сокращая время вычислений (см. Сложность).

После выбора оптимального разделения \(\theta^*\) в узле \(m\), та же процедура разделения затем рекурсивно применяется к каждому разделу \(Q_m^{left}(\theta^*)\) и \(Q_m^{right}(\theta^*)\) до тех пор, пока не будет достигнуто условие остановки, такое как:

  • Количество компонент. Еслиmax_depth);

  • \(n_m\) меньше, чем min_samples_split;

  • уменьшение примеси для этого разделения меньше, чем min_impurity_decrease.

См. документацию соответствующего оценщика для других условий остановки.

1.10.7.1. Критерии классификации#

Если целевая переменная является классификационным исходом, принимающим значения 0,1,…,K-1, для узла \(m\), пусть

\[p_{mk} = \frac{1}{n_m} \sum_{y \in Q_m} I(y = k)\]

будет долей наблюдений класса k в узле \(m\). Если \(m\) является терминальным узлом, predict_proba для этого региона установлено \(p_{mk}\). Общие меры неопределенности следующие.

Джини:

\[H(Q_m) = \sum_k p_{mk} (1 - p_{mk})\]

Логарифмическая потеря или энтропия:

\[H(Q_m) = - \sum_k p_{mk} \log(p_{mk})\]
Энтропия Шеннона#

Критерий энтропии вычисляет энтропию Шеннона возможных классов. Он использует частоты классов обучающих точек данных, достигших данного листа \(m\) как их вероятность. Используя Энтропия Шеннона как критерий разделения узлов дерева эквивалентна минимизации логарифмических потерь (также известное как кросс-энтропия и мультиномиальный девнанс) между истинными метками \(y_i\) и вероятностные предсказания \(T_k(x_i)\) модели дерева \(T\) для класса \(k\).

Чтобы увидеть это, сначала вспомним, что лог-лосс модели дерева \(T\) вычисленный на наборе данных \(D\) определяется следующим образом:

\[\mathrm{LL}(D, T) = -\frac{1}{n} \sum_{(x_i, y_i) \in D} \sum_k I(y_i = k) \log(T_k(x_i))\]

где \(D\) является обучающим набором данных \(n\) пары \((x_i, y_i)\).

В классификационном дереве предсказанные вероятности классов внутри листовых узлов постоянны, то есть: для всех \((x_i, y_i) \in Q_m\), имеем: \(T_k(x_i) = p_{mk}\) для каждого класса \(k\).

Это свойство позволяет переписать \(\mathrm{LL}(D, T)\) как сумма энтропий Шеннона, вычисленных для каждого листа \(T\) взвешенный по количеству обучающих точек данных, достигших каждого листа:

\[\mathrm{LL}(D, T) = \sum_{m \in T} \frac{n_m}{n} H(Q_m)\]

1.10.7.2. Критерии регрессии#

Если цель - непрерывное значение, то для узла \(m\), общие критерии для минимизации, как для определения мест для будущих разбиений, — это Среднеквадратичная ошибка (MSE или ошибка L2), отклонение Пуассона, а также Средняя Абсолютная ошибка (MAE или ошибка L1). MSE и отклонение Пуассона оба устанавливают прогнозируемое значение терминальных узлов в изученное среднее значение \(\bar{y}_m\) узла, тогда как MAE устанавливает прогнозируемое значение конечных узлов равным медиане \(median(y)_m\).

Среднеквадратичная ошибка:

\[ \begin{align}\begin{aligned}\bar{y}_m = \frac{1}{n_m} \sum_{y \in Q_m} y\\H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} (y - \bar{y}_m)^2\end{aligned}\end{align} \]

Среднее отклонение Пуассона:

\[H(Q_m) = \frac{2}{n_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} - y + \bar{y}_m)\]

Установка criterion="poisson" может быть хорошим выбором, если ваша цель — это количество или частота (количество на некоторую единицу). В любом случае, \(y >= 0\) является необходимым условием для использования этого критерия. По соображениям производительности фактическая реализация минимизирует половину среднего отклонения Пуассона, т.е. среднее отклонение Пуассона, деленное на 2.

Средняя абсолютная ошибка:

\[ \begin{align}\begin{aligned}median(y)_m = \underset{y \in Q_m}{\mathrm{median}}(y)\\H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} |y - median(y)_m|\end{aligned}\end{align} \]

Обратите внимание, что обучение в 3–6 раз медленнее, чем критерий MSE, начиная с версии 1.8.

1.10.8. Поддержка пропущенных значений#

DecisionTreeClassifier, DecisionTreeRegressor имеют встроенную поддержку пропущенных значений с использованием splitter='best', где разбиения определяются жадным образом. ExtraTreeClassifier, и ExtraTreeRegressor имеют встроенную поддержку пропущенных значений для splitter='random', где разбиения определяются случайным образом. Для получения дополнительных сведений о том, как разделитель отличается для ненулевых значений, см. Раздел Forest.

Критерии, поддерживаемые при наличии пропущенных значений: 'gini', 'entropy', или 'log_loss', для классификации или 'squared_error', 'friedman_mse', или 'poisson' для регрессии.

Сначала мы опишем, как DecisionTreeClassifier, DecisionTreeRegressor обрабатывать пропущенные значения в данных.

Для каждого потенциального порога на данных без пропусков разделитель оценит разбиение, при котором все пропущенные значения отправляются в левый или правый узел.

Решения принимаются следующим образом:

  • По умолчанию при предсказании образцы с пропущенными значениями классифицируются с использованием класса, найденного при обучении:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 6, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0).fit(X, y)
>>> tree.predict(X)
array([0, 0, 1, 1])

  • Если оценка критерия одинакова для обоих узлов, то ничья для пропущенного значения во время предсказания разрешается переходом в правый узел. Разделитель также проверяет разделение, где все пропущенные значения идут в один дочерний узел, а не пропущенные значения — в другой:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([np.nan, -1, np.nan, 1]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0, max_depth=1).fit(X, y)

>>> X_test = np.array([np.nan]).reshape(-1, 1)
>>> tree.predict(X_test)
array([1])

  • Если во время обучения для данного признака не было пропущенных значений, то во время предсказания пропущенные значения отображаются на дочерний узел с наибольшим количеством образцов:

    >>> from sklearn.tree import DecisionTreeClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 2, 3]).reshape(-1, 1)
>>> y = [0, 1, 1, 1]

>>> tree = DecisionTreeClassifier(random_state=0).fit(X, y)

>>> X_test = np.array([np.nan]).reshape(-1, 1)
>>> tree.predict(X_test)
array([1])

ExtraTreeClassifier, и ExtraTreeRegressor обрабатывать пропущенные значения немного иначе. При разделении узла случайный порог будет выбран для разделения непропущенных значений. Затем непропущенные значения будут отправлены в левый и правый дочерние узлы на основе случайно выбранного порога, а пропущенные значения также будут случайно отправлены в левый или правый дочерний узел. Это повторяется для каждого признака, рассматриваемого при каждом разделении. Выбирается лучшее разделение среди них.

При предсказании обработка пропущенных значений такая же, как у дерева решений:

  • По умолчанию при прогнозировании образцы с пропущенными значениями классифицируются с классом, использованным в разделе, найденном во время обучения.

  • Если во время обучения для данного признака не было пропущенных значений, то во время предсказания пропущенные значения сопоставляются с дочерним узлом, имеющим наибольшее количество образцов.

1.10.9. Минимальная обрезка по стоимости-сложности#

Минимальное обрезание по стоимости-сложности — это алгоритм, используемый для обрезки дерева, чтобы избежать переобучения, описанный в главе 3 [BRE]. Этот алгоритм параметризуется параметром \(\alpha\ge0\) известный как параметр сложности. Параметр сложности используется для определения меры стоимости-сложности, \(R_\alpha(T)\) данного дерева \(T\):

\[R_\alpha(T) = R(T) + \alpha|\widetilde{T}|\]

где \(|\widetilde{T}|\) это количество терминальных узлов в \(T\) и \(R(T)\) традиционно определяется как общая частота ошибочной классификации терминальных узлов. В качестве альтернативы scikit-learn использует общую взвешенную примесь выборки терминальных узлов для \(R(T)\). Как показано выше, нечистота узла зависит от критерия. Обрезка с минимальной стоимостью-сложностью находит поддерево \(T\) который минимизирует \(R_\alpha(T)\).

Мера сложности стоимости одного узла равна \(R_\alpha(t)=R(t)+\alpha\). Ветка, \(T_t\), определяется как дерево, где узел \(t\) является его корнем. В общем случае, нечистота узла больше суммы нечистот его терминальных узлов, \(R(T_t). Однако мера стоимости сложности узла, \(t\), и его ветвь, \(T_t\), могут быть равны в зависимости от \(\alpha\). Мы определяем эффективный \(\alpha\) узла быть значением, где они равны, \(R_\alpha(T_t)=R_\alpha(t)\) или \(\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}\). Не терминальный узел с наименьшим значением \(\alpha_{eff}\) является самым слабым звеном и будет обрезан. Этот процесс останавливается, когда минимальное \(\alpha_{eff}\) больше, чем ccp_alpha параметр.

Примеры

Ссылки

[BRE]

L. Breiman, J. Friedman, R. Olshen и C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.