2.4. Бикластеризация#
Алгоритмы бикластеризации одновременно кластеризуют строки и столбцы матрицы данных. Эти кластеры строк и столбцов известны как бикластеры. Каждый определяет подматрицу исходной матрицы данных с некоторыми желаемыми свойствами.
Например, для матрицы формы (10, 10), один возможный бикластер
с тремя строками и двумя столбцами индуцирует подматрицу формы (3, 2):
>>> import numpy as np
>>> data = np.arange(100).reshape(10, 10)
>>> rows = np.array([0, 2, 3])[:, np.newaxis]
>>> columns = np.array([1, 2])
>>> data[rows, columns]
array([[ 1, 2],
[21, 22],
[31, 32]])
Для целей визуализации, при наличии бикластера, строки и столбцы матрицы данных могут быть переупорядочены, чтобы сделать бикластер непрерывным.
Алгоритмы различаются в том, как они определяют бикластеры. Некоторые из распространённых типов включают:
постоянные значения, постоянные строки или постоянные столбцы
необычно высокие или низкие значения
подматрицы с низкой дисперсией
коррелированные строки или столбцы
Алгоритмы также различаются по тому, как строки и столбцы могут быть назначены бикластерам, что приводит к разным структурам бикластеров. Блочно-диагональные или шахматные структуры возникают, когда строки и столбцы разделены на разделы.
Если каждая строка и каждый столбец принадлежат ровно одному бикластеру, то перестановка строк и столбцов матрицы данных выявляет бикластеры на диагонали. Вот пример такой структуры, где бикластеры имеют более высокие средние значения, чем другие строки и столбцы:
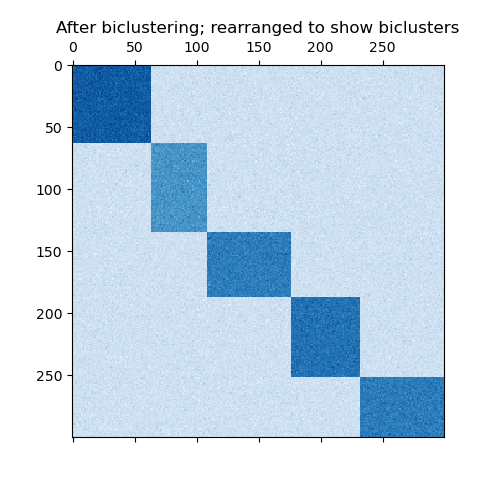
Пример бикластеров, сформированных разделением строк и столбцов.#
В случае шахматной доски каждая строка принадлежит всем кластерам столбцов, и каждый столбец принадлежит всем кластерам строк. Вот пример этой структуры, где дисперсия значений внутри каждого бикластера мала:
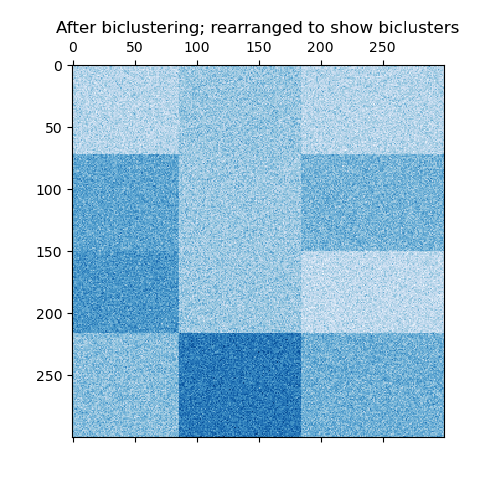
Пример шахматных бикластеров.#
После обучения модели членство в кластерах строк и столбцов можно найти в rows_ и columns_ атрибуты. rows_[i] является бинарным вектором с ненулевыми элементами, соответствующими строкам, принадлежащим бикластеру
i. Аналогично, columns_[i] указывает, какие столбцы принадлежат
бикластеру i.
Некоторые модели также имеют row_labels_ и column_labels_ атрибуты. Эти модели разделяют строки и столбцы, как в блочно-диагональной и шахматной структурах бикластеров.
Примечание
Бикластеризация имеет много других названий в различных областях, включая ко-кластеризацию, двухрежимную кластеризацию, двустороннюю кластеризацию, блочную кластеризацию, связанную двустороннюю кластеризацию и т.д. Названия некоторых алгоритмов, таких как алгоритм спектральной ко-кластеризации, отражают эти альтернативные названия.
2.4.1. Спектральная совместная кластеризация#
The SpectralCoclustering алгоритм находит бикластеры с
значениями выше, чем в соответствующих других строках и столбцах.
Каждая строка и каждый столбец принадлежат ровно одному бикластеру, поэтому
перестановка строк и столбцов для создания непрерывных разделов выявляет
эти высокие значения вдоль диагонали:
Примечание
Алгоритм рассматривает входную матрицу данных как двудольный граф: строки и столбцы матрицы соответствуют двум множествам вершин, а каждая запись соответствует ребру между строкой и столбцом. Алгоритм аппроксимирует нормализованный разрез этого графа, чтобы найти тяжёлые подграфы.
2.4.1.1. Математическая формулировка#
Приближенное решение оптимального нормализованного разреза может быть найдено через обобщенное разложение по собственным значениям лапласиана графа. Обычно это означает работу непосредственно с матрицей лапласиана. Если исходная матрица данных \(A\) имеет форму \(m \times n\), матрица Лапласа для соответствующего двудольного графа имеет форму \((m + n) \times (m + n)\). Однако в этом случае можно работать напрямую с \(A\), который меньше и эффективнее.
Входная матрица \(A\) предварительно обрабатывается следующим образом:
Где \(R\) является диагональной матрицей с записью \(i\) равно \(\sum_{j} A_{ij}\) и \(C\) — это диагональная матрица с элементом \(j\) равно \(\sum_{i} A_{ij}\).
Сингулярное разложение, \(A_n = U \Sigma V^\top\), предоставляет разделения строк и столбцов \(A\). Подмножество левых сингулярных векторов даёт разделение строк, а подмножество правых сингулярных векторов даёт разделение столбцов.
The \(\ell = \lceil \log_2 k \rceil\) сингулярные векторы, начиная со второго, предоставляют необходимую информацию о разделении. Они используются для формирования матрицы \(Z\):
где столбцы \(U\) являются \(u_2, \dots, u_{\ell + 1}\), и аналогично для \(V\).
Затем строки \(Z\) кластеризуются с использованием k-means. Первый n_rows метки обеспечивают разделение по строкам, а оставшиеся n_columns метки обеспечивают разделение по столбцам.
Примеры
Демонстрация алгоритма спектральной совместной кластеризации: Простой пример, показывающий, как сгенерировать матрицу данных с бикластерами и применить этот метод к ней.
Бикластеризация документов с помощью алгоритма спектральной совместной кластеризации: Пример нахождения бикластеров в наборе данных двадцати новостных групп.
Ссылки
Dhillon, Inderjit S, 2001. Совместная кластеризация документов и слов с использованием биспектрального разделения графа
2.4.2. Спектральная бикластеризация#
The SpectralBiclustering алгоритм предполагает, что входная матрица данных имеет скрытую шахматную структуру. Строки и столбцы матрицы с такой структурой могут быть разделены так, что элементы любого бикластера в декартовом произведении кластеров строк и столбцов приблизительно постоянны. Например, если есть два раздела строк и три раздела столбцов, каждая строка будет принадлежать трём бикластерам, а каждый столбец — двум бикластерам.
Алгоритм разделяет строки и столбцы матрицы так, чтобы соответствующая блочно-постоянная шахматная матрица обеспечивала хорошее приближение к исходной матрице.
2.4.2.1. Математическая формулировка#
Входная матрица \(A\) сначала нормализуется, чтобы сделать шахматный узор более очевидным. Существует три возможных метода:
Независимая нормализация строк и столбцов, как в спектральной совместной кластеризации. Этот метод делает суммы строк постоянными, а суммы столбцов – другой постоянной.
Бистохастизация: повторная нормализация строк и столбцов до сходимости. Этот метод делает так, что и строки, и столбцы суммируются до одной и той же константы.
Логарифмическая нормализация: вычисляется логарифм матрицы данных: \(L = \log A\). Затем среднее значение столбца \(\overline{L_{i \cdot}}\), среднее по строкам \(\overline{L_{\cdot j}}\), и общее среднее \(\overline{L_{\cdot \cdot}}\) of \(L\) вычисляются. Итоговая матрица вычисляется по формуле
После нормализации вычисляются первые несколько сингулярных векторов, как в алгоритме Spectral Co-Clustering.
Если использовалась логарифмическая нормализация, все сингулярные векторы значимы. Однако, если использовалась независимая нормализация или бистохастизация, первые сингулярные векторы, \(u_1\) и \(v_1\). отбрасываются. Отныне «первые» сингулярные векторы относятся к \(u_2 \dots u_{p+1}\) и \(v_2 \dots v_{p+1}\) за исключением случая логарифмической нормализации.
Учитывая эти сингулярные векторы, они ранжируются в соответствии с тем, какой из них может быть наилучшим образом аппроксимирован кусочно-постоянным вектором. Аппроксимации для каждого вектора находятся с использованием одномерного k-средних и оцениваются с помощью евклидова расстояния. Выбирается некоторое подмножество лучших левых и правых сингулярных векторов. Затем данные проецируются на это лучшее подмножество сингулярных векторов и кластеризуются.
Например, если \(p\) сингулярные векторы были вычислены,
\(q\) лучшие находятся как описано, где \(q
Примеры
Демонстрация алгоритма Spectral Biclustering: простой пример показывающий, как сгенерировать шахматную матрицу и выполнить бикластеризацию.
Ссылки
Kluger, Yuval, et. al., 2003. Спектральная бикластеризация данных микрочипов: совместная кластеризация генов и условий
2.4.3. Оценка бикластеризации#
Существует два способа оценки результата бикластеризации: внутренний и внешний. Внутренние меры, такие как стабильность кластеров, опираются только на данные и сам результат. В настоящее время в scikit-learn нет внутренних мер бикластеризации. Внешние меры ссылаются на внешний источник информации, такой как истинное решение. При работе с реальными данными истинное решение обычно неизвестно, но бикластеризация искусственных данных может быть полезна для оценки алгоритмов именно потому, что истинное решение известно.
Для сравнения набора найденных бикластеров с набором истинных бикластеров необходимы две меры сходства: мера сходства для отдельных бикластеров и способ объединения этих индивидуальных сходств в общую оценку.
Для сравнения отдельных бикластеров использовалось несколько мер. На данный момент реализован только индекс Жаккара:
где \(A\) и \(B\) являются бикластерами, \(|A \cap B|\) это количество элементов в их пересечении. Индекс Жаккара достигает своего минимума 0, когда бикластеры вообще не перекрываются, и максимума 1, когда они идентичны.
Было разработано несколько методов для сравнения двух наборов бикластеров.
На данный момент только consensus_score (Хохрейтер и др., 2010) доступен:
Вычислить сходства бикластеров для пар бикластеров, по одному в каждом наборе, используя индекс Жаккара или аналогичную меру.
Назначьте бикластеры из одного набора другому в соответствии один к одному, чтобы максимизировать сумму их сходств. Этот шаг выполняется с использованием
scipy.optimize.linear_sum_assignment, который использует модифицированный алгоритм Йонкера-Волгенанта.Итоговая сумма сходств делится на размер большего множества.
Минимальный консенсусный балл, 0, достигается, когда все пары бикластеров полностью различны. Максимальный балл, 1, достигается, когда оба множества идентичны.
Ссылки
Hochreiter, Bodenhofer, et. al., 2010. FABIA: факторный анализ для получения бикластеров.