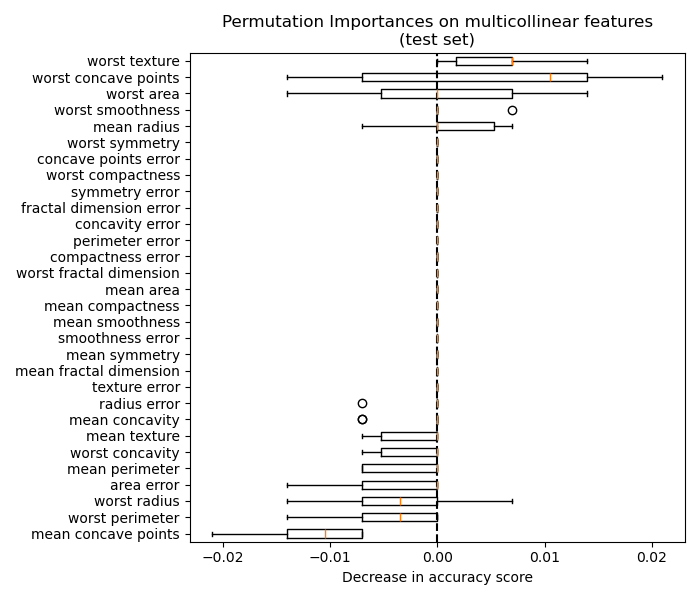
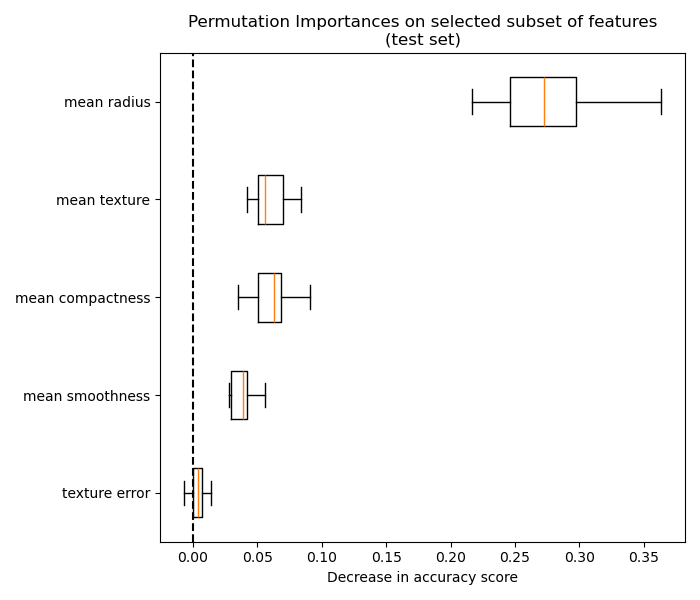
5.2. Важность признаков на основе перестановок#

Важность признаков на основе перестановок — это техника инспекции модели, которая измеряет вклад каждого признака в обученный статистическая производительность модели на заданном табличном наборе данных. Эта техника особенно полезна для нелинейных или непрозрачных оценщики, и включает случайное перемешивание значений одного признака и наблюдение за результирующим ухудшением оценки модели [1]. Разрывая связь между признаком и целевой переменной, мы определяем, насколько модель полагается на этот конкретный признак.

На следующих рисунках мы наблюдаем эффект перестановки признаков на корреляцию между признаком и целевой переменной и, следовательно, на статистическую производительность модели.

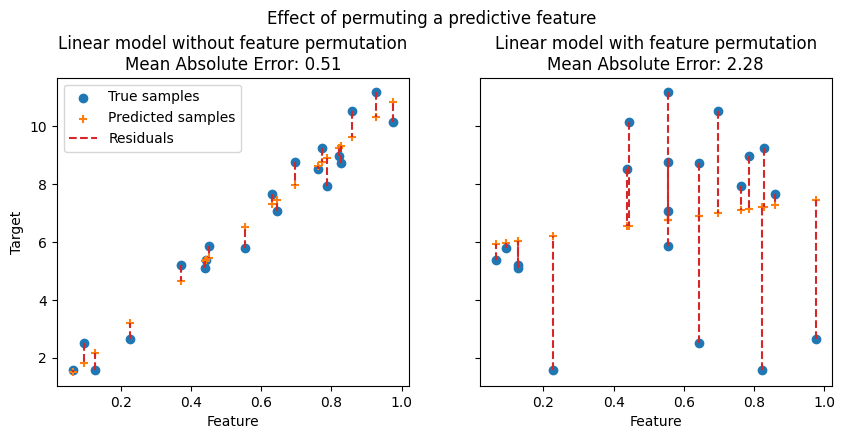
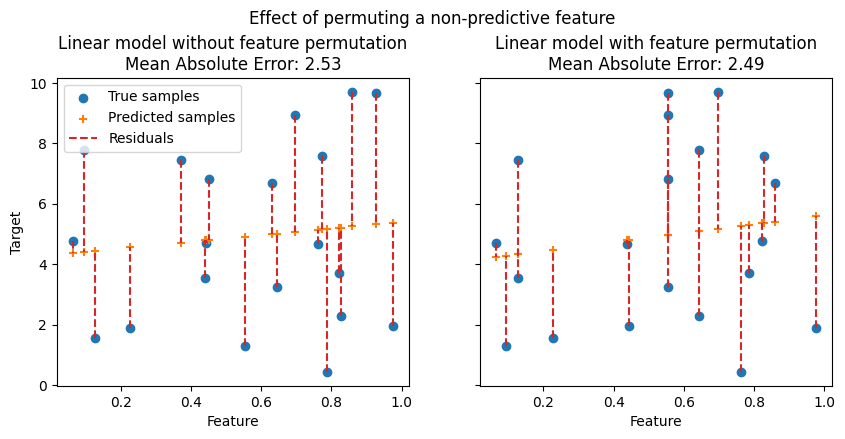
../_images/permuted_predictive_feature.png ../_images/permuted_non_predictive_feature.png

На верхнем графике мы видим, что перестановка прогностического признака нарушает корреляцию между признаком и целевой переменной, и, как следствие, статистическая производительность модели снижается. На нижнем графике мы видим, что перестановка непрогностического признака не приводит к значительному ухудшению статистической производительности модели.

Одно ключевое преимущество важности характеристик на основе перестановок заключается в том, что оно не зависит от модели, т.е. может применяться к любому обученному оценщику. Более того, его можно рассчитать несколько раз с разными перестановками характеристик, дополнительно предоставляя меру дисперсии в оценённой важности характеристик для конкретной обученной модели.

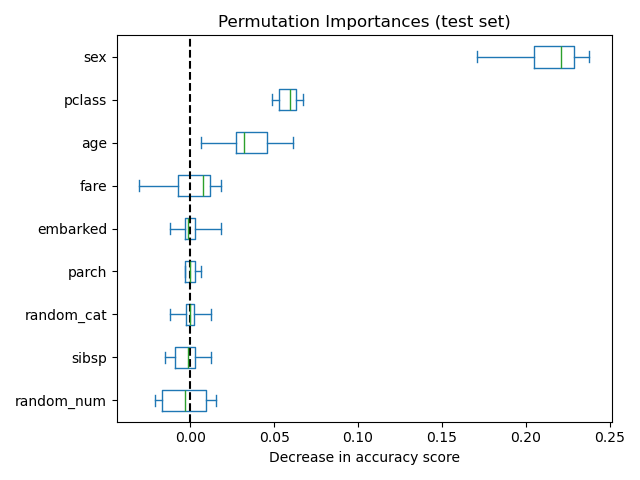
На рисунке ниже показана важность признаков на основе перестановок для RandomForestClassifier обучен на расширенной версии набора данных titanic, который содержит random_cat и random_num признаки, т.е. категориальный и числовой признаки, которые никак не коррелируют с целевой переменной:

../_images/sphx_glr_plot_permutation_importance_002.png

Предупреждение

Признаки, которые считаются низкая важность для плохой модели (низкая оценка перекрестной проверки) может быть очень важно для хорошей модели. Поэтому всегда важно оценивать предсказательную способность модели на отложенной выборке (или лучше с перекрестной проверкой) перед вычислением важности признаков. Перестановочная важность не отражает внутреннюю предсказательную ценность признака сам по себе, а насколько важна эта характеристика для конкретной модели.

The permutation_importance функция вычисляет важность признаков для оценщики для заданного набора данных. n_repeats параметр устанавливает количество случайных перестановок признака и возвращает выборку важностей признаков.

Рассмотрим следующую обученную регрессионную модель:

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import Ridge
>>> diabetes = load_diabetes()
>>> X_train, X_val, y_train, y_val = train_test_split(
...     diabetes.data, diabetes.target, random_state=0)
...
>>> model = Ridge(alpha=1e-2).fit(X_train, y_train)
>>> model.score(X_val, y_val)
0.356...

Его производительность на валидации, измеренная через \(R^2\) оценка, значительно больше, чем уровень случайности. Это позволяет использовать permutation_importance функция для исследования, какие признаки наиболее предсказуемы:

>>> from sklearn.inspection import permutation_importance
>>> r = permutation_importance(model, X_val, y_val,
...                            n_repeats=30,
...                            random_state=0)
...
>>> for i in r.importances_mean.argsort()[::-1]:
...     if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
...         print(f"{diabetes.feature_names[i]:<8}"
...               f"{r.importances_mean[i]:.3f}"
...               f" +/- {r.importances_std[i]:.3f}")
...
s5      0.204 +/- 0.050
bmi     0.176 +/- 0.048
bp      0.088 +/- 0.033
sex     0.056 +/- 0.023

Обратите внимание, что значения важности для главных признаков представляют большую долю эталонного показателя 0.356.

Перестановочные важности могут быть вычислены либо на обучающем наборе, либо на отложенном тестовом или валидационном наборе. Использование отложенного набора позволяет выделить, какие признаки вносят наибольший вклад в обобщающую способность исследуемой модели. Признаки, которые важны на обучающем наборе, но не на отложенном, могут вызывать переобучение модели.

Важность признаков на основе перестановки зависит от функции оценки, которая указана с помощью scoring аргумент. Этот аргумент принимает несколько оценщиков, что вычислительно эффективнее, чем последовательный вызов permutation_importance несколько раз с разными оценщиками, так как он повторно использует предсказания модели.

Пример перестановочной важности признаков с использованием нескольких оценщиков#

В примере ниже мы используем список метрик, но возможны и другие форматы ввода, как описано в Использование оценки по нескольким метрикам.

>>> scoring = ['r2', 'neg_mean_absolute_percentage_error', 'neg_mean_squared_error']
>>> r_multi = permutation_importance(
...     model, X_val, y_val, n_repeats=30, random_state=0, scoring=scoring)
...
>>> for metric in r_multi:
...     print(f"{metric}")
...     r = r_multi[metric]
...     for i in r.importances_mean.argsort()[::-1]:
...         if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
...             print(f"    {diabetes.feature_names[i]:<8}"
...                   f"{r.importances_mean[i]:.3f}"
...                   f" +/- {r.importances_std[i]:.3f}")
...
r2
    s5      0.204 +/- 0.050
    bmi     0.176 +/- 0.048
    bp      0.088 +/- 0.033
    sex     0.056 +/- 0.023
neg_mean_absolute_percentage_error
    s5      0.081 +/- 0.020
    bmi     0.064 +/- 0.015
    bp      0.029 +/- 0.010
neg_mean_squared_error
    s5      1013.866 +/- 246.445
    bmi     872.726 +/- 240.298
    bp      438.663 +/- 163.022
    sex     277.376 +/- 115.123

Ранжирование признаков примерно одинаково для разных метрик, даже если масштабы значений важности очень разные. Однако это не гарантируется, и разные метрики могут привести к значительно разным важностям признаков, особенно для моделей, обученных на несбалансированных задачах классификации, для которых выбор метрики классификации может быть критическим.

5.2.1. Обзор алгоритма важности перестановок#

  • Входные данные: обученная прогнозная модель \(m\), табличный набор данных (обучающий или валидационный) \(D\).

  • Вычислить эталонную оценку \(s\) модели \(m\) на данных \(D\) (например, точность для классификатора или \(R^2\) для регрессора).

  • Для каждого признака \(j\) (столбец \(D\)):

    • Для каждого повторения \(k\) в \({1, ..., K}\):

      • Случайное перемешивание столбца \(j\) набора данных \(D\) для генерации искаженной версии данных, названной \(\tilde{D}_{k,j}\).

      • Вычислить оценку \(s_{k,j}\) модели \(m\) на поврежденных данных \(\tilde{D}_{k,j}\).

    • Вычислить важность \(i_j\) для признака \(f_j\) определяется как:

      \[i_j = s - \frac{1}{K} \sum_{k=1}^{K} s_{k,j}\]

5.2.2. Связь с важностью на основе примесей в деревьях#

Древовидные модели предоставляют альтернативную меру важность признаков на основе среднего уменьшения примесей (MDI). Нечистота количественно оценивается критерием разделения деревьев решений (Джини, Логарифмические потери или Среднеквадратичная ошибка). Однако этот метод может придавать высокую важность признакам, которые могут не быть предсказательными на невидимых данных, когда модель переобучается. С другой стороны, важность признаков на основе перестановок избегает этой проблемы, поскольку может быть вычислена на невидимых данных.

Кроме того, важность признаков на основе нечистоты для деревьев сильно смещен и предпочитать признаки с высокой кардинальностью (обычно числовые признаки) над признаками с низкой кардинальностью, такими как бинарные признаки или категориальные переменные с небольшим количеством возможных категорий.

Важности признаков на основе перестановок не проявляют такого смещения. Кроме того, важность признаков на основе перестановок может быть вычислена с любой метрикой производительности на предсказаниях модели и может использоваться для анализа любого класса моделей (не только моделей на основе деревьев).

Следующий пример демонстрирует ограничения важности признаков на основе нечистоты в сравнении с важностью признаков на основе перестановок: Важность перестановок против важности признаков случайного леса (MDI).

5.2.3. Вводящие в заблуждение значения на сильно коррелированных признаках#

Когда два признака коррелируют и один из признаков переставлен, модель все еще имеет доступ к последнему через его коррелированный признак. Это приводит к более низкому заявленному значению важности для обоих признаков, хотя они могут фактически может быть важным.

На рисунке ниже показана важность признаков на основе перестановок для RandomForestClassifier обучен с использованием Набор данных о раке молочной железы в Висконсине (диагностический), который содержит сильно коррелированные признаки. Наивная интерпретация может предположить, что все признаки не важны:

../_images/sphx_glr_plot_permutation_importance_multicollinear_002.png

Один из способов справиться с проблемой — кластеризовать коррелированные признаки и оставить только один признак из каждого кластера.

../_images/sphx_glr_plot_permutation_importance_multicollinear_004.png

Для получения более подробной информации о такой стратегии см. пример Важность перестановок с мультиколлинеарными или коррелированными признаками.

Примеры

Ссылки