Изотоническая регрессия

Иллюстрация изотонной регрессии на сгенерированных данных (нелинейный монотонный тренд с гомоскедастичным равномерным шумом).

Алгоритм изотонной регрессии находит неубывающую аппроксимацию функции, минимизируя среднеквадратичную ошибку на обучающих данных. Преимущество такой непараметрической модели в том, что она не предполагает какой-либо формы для целевой функции, кроме монотонности. Для сравнения также представлена линейная регрессия.

График на правой стороне показывает функцию предсказания модели, которая получается в результате линейной интерполяции пороговых точек. Пороговые точки — это подмножество входных наблюдений обучения, и их соответствующие целевые значения вычисляются с помощью изотонической непараметрической подгонки.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import LineCollection

from sklearn.isotonic import IsotonicRegression
from sklearn.linear_model import LinearRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50.0 * np.log1p(np.arange(n))

Обучить модели IsotonicRegression и LinearRegression:

ir = IsotonicRegression(out_of_bounds="clip")
y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  # x needs to be 2d for LinearRegression

LinearRegression()

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Построить результаты:

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 6))

ax0.plot(x, y, "C0.", markersize=12)
ax0.plot(x, y_, "C1.-", markersize=12)
ax0.plot(x, lr.predict(x[:, np.newaxis]), "C2-")
ax0.add_collection(lc)
ax0.legend(("Training data", "Isotonic fit", "Linear fit"), loc="lower right")
ax0.set_title("Isotonic regression fit on noisy data (n=%d)" % n)

x_test = np.linspace(-10, 110, 1000)
ax1.plot(x_test, ir.predict(x_test), "C1-")
ax1.plot(ir.X_thresholds_, ir.y_thresholds_, "C1.", markersize=12)
ax1.set_title("Prediction function (%d thresholds)" % len(ir.X_thresholds_))

plt.show()

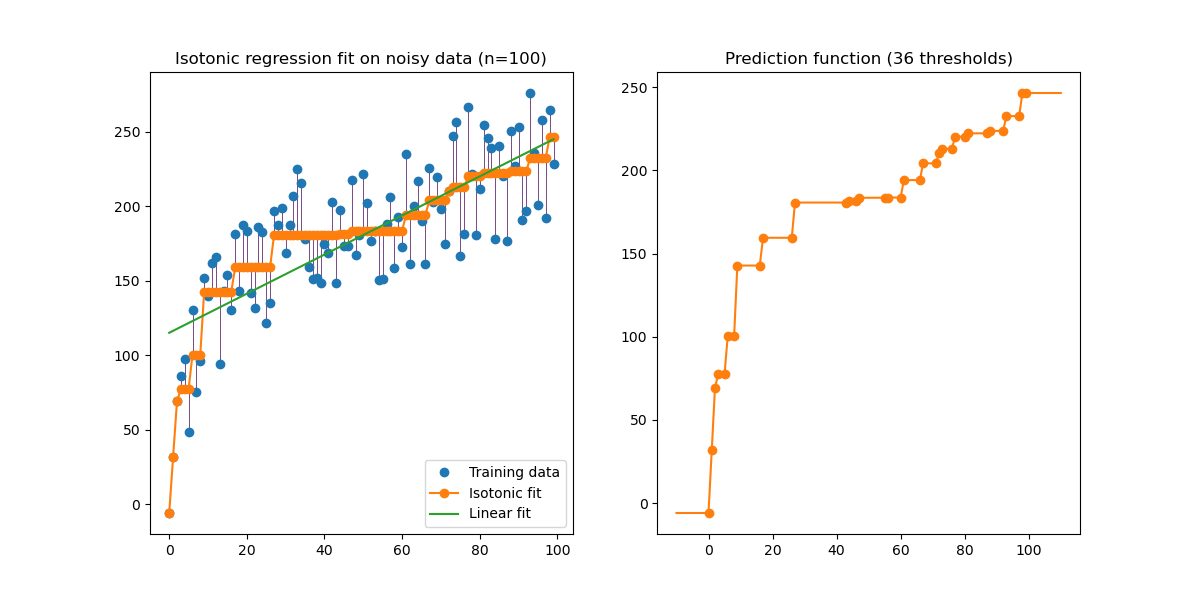
Обратите внимание, что мы явно передали out_of_bounds="clip" в конструктор IsotonicRegression для управления способом экстраполяции модели за пределы диапазона данных, наблюдаемых в обучающем наборе. Эта "отсечка" экстраполяции может быть видна на графике решающей функции справа.

Связанные примеры

Эффект преобразования целей в регрессионной модели

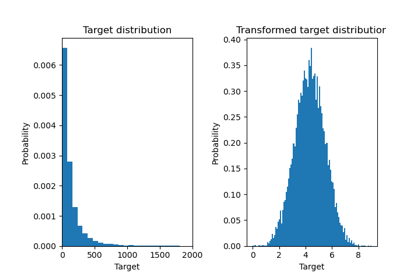
Эффект преобразования целей в регрессионной модели

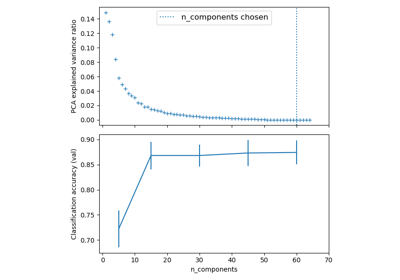
Конвейеризация: объединение PCA и логистической регрессии

Конвейеризация: объединение PCA и логистической регрессии

Кривые калибровки вероятности

Кривые калибровки вероятности

Калибровка вероятностей классификаторов

Калибровка вероятностей классификаторов