Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Графики частичной зависимости и индивидуального условного ожидания#
Графики частной зависимости показывают зависимость между целевой функцией [2] и набор интересующих признаков, маргинализируя по значениям всех других признаков (дополнительных признаков). Из-за ограничений человеческого восприятия размер набора интересующих признаков должен быть небольшим (обычно один или два), поэтому они обычно выбираются среди наиболее важных признаков.
Аналогично, график индивидуального условного ожидания (ICE) [3] показывает зависимость между целевой функцией и интересующим признаком. Однако, в отличие от графиков частичной зависимости, которые показывают средний эффект интересующих признаков, ICE-графики визуализируют зависимость предсказания от признака для каждого sample отдельно, с одной строкой на образец. Только один интересующий признак поддерживается для ICE-графиков.
Этот пример показывает, как получить графики частичной зависимости и ICE из
MLPRegressor и
HistGradientBoostingRegressor обученная на наборе данных о прокате велосипедов. Пример вдохновлен [1].
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Предобработка набора данных о прокате велосипедов#
Мы будем использовать набор данных о прокате велосипедов. Цель — предсказать количество прокатов велосипедов, используя данные о погоде и сезоне, а также информацию о дате и времени.
from sklearn.datasets import fetch_openml
bikes = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
# Make an explicit copy to avoid "SettingWithCopyWarning" from pandas
X, y = bikes.data.copy(), bikes.target
# We use only a subset of the data to speed up the example.
X = X.iloc[::5, :]
y = y[::5]
Признак "weather" имеет особенность: категория "heavy_rain" является редкой
категорией.
X["weather"].value_counts()
weather
clear 2284
misty 904
rain 287
heavy_rain 1
Name: count, dtype: int64
Из-за этой редкой категории мы объединяем ее в "rain".
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
Теперь мы подробнее рассмотрим "year" признак:
X["year"].value_counts()
year
1 1747
0 1729
Name: count, dtype: int64
Мы видим, что у нас есть данные за два года. Мы используем первый год для обучения модели, а второй год - для тестирования модели.
mask_training = X["year"] == 0.0
X = X.drop(columns=["year"])
X_train, y_train = X[mask_training], y[mask_training]
X_test, y_test = X[~mask_training], y[~mask_training]
Мы можем проверить информацию о наборе данных, чтобы увидеть, что у нас есть разнородные типы данных. Мы должны предварительно обработать различные столбцы соответствующим образом.
X_train.info()
Index: 1729 entries, 0 to 8640
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 season 1729 non-null category
1 month 1729 non-null int64
2 hour 1729 non-null int64
3 holiday 1729 non-null category
4 weekday 1729 non-null int64
5 workingday 1729 non-null category
6 weather 1729 non-null category
7 temp 1729 non-null float64
8 feel_temp 1729 non-null float64
9 humidity 1729 non-null float64
10 windspeed 1729 non-null float64
dtypes: category(4), float64(4), int64(3)
memory usage: 115.4 KB
Из предыдущей информации мы рассмотрим category столбцы как номинальные категориальные признаки. Кроме того, мы будем рассматривать информацию о дате и времени как категориальные признаки.
Мы вручную определяем столбцы, содержащие числовые и категориальные признаки.
numerical_features = [
"temp",
"feel_temp",
"humidity",
"windspeed",
]
categorical_features = X_train.columns.drop(numerical_features)
Прежде чем мы углубимся в детали предварительной обработки различных конвейеров машинного обучения, мы попытаемся получить дополнительную интуицию относительно набора данных, которая поможет понять статистическую производительность модели и результаты анализа частичной зависимости.
Мы строим график среднего количества аренд велосипедов, группируя данные по сезонам и по годам.
from itertools import product
import matplotlib.pyplot as plt
import numpy as np
days = ("Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat")
hours = tuple(range(24))
xticklabels = [f"{day}\n{hour}:00" for day, hour in product(days, hours)]
xtick_start, xtick_period = 6, 12
fig, axs = plt.subplots(nrows=2, figsize=(8, 6), sharey=True, sharex=True)
average_bike_rentals = bikes.frame.groupby(
["year", "season", "weekday", "hour"], observed=True
).mean(numeric_only=True)["count"]
for ax, (idx, df) in zip(axs, average_bike_rentals.groupby("year")):
df.groupby("season", observed=True).plot(ax=ax, legend=True)
# decorate the plot
ax.set_xticks(
np.linspace(
start=xtick_start,
stop=len(xticklabels),
num=len(xticklabels) // xtick_period,
)
)
ax.set_xticklabels(xticklabels[xtick_start::xtick_period])
ax.set_xlabel("")
ax.set_ylabel("Average number of bike rentals")
ax.set_title(
f"Bike rental for {'2010 (train set)' if idx == 0.0 else '2011 (test set)'}"
)
ax.set_ylim(0, 1_000)
ax.set_xlim(0, len(xticklabels))
ax.legend(loc=2)
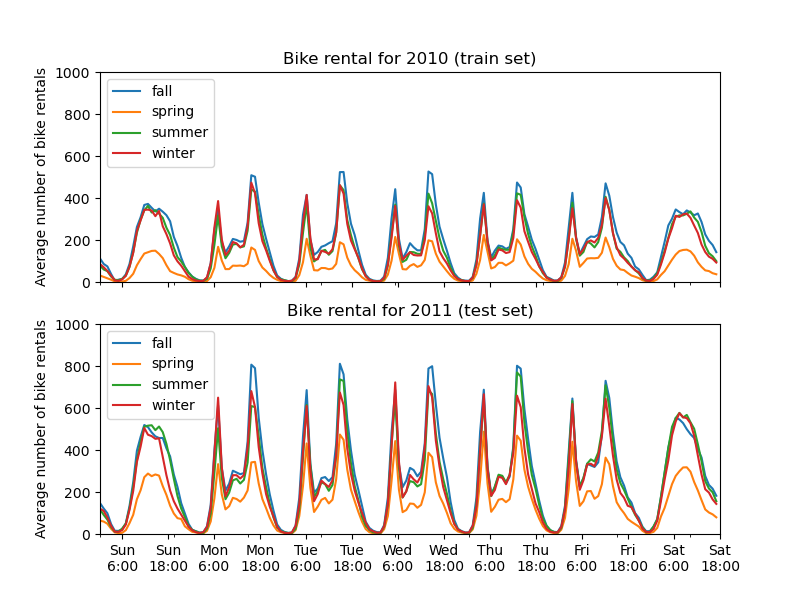
Первое заметное различие между обучающим и тестовым наборами данных заключается в том, что количество прокатов велосипедов выше в тестовом наборе. По этой причине неудивительно получить модель машинного обучения, которая недооценивает количество прокатов велосипедов. Мы также наблюдаем, что количество прокатов велосипедов ниже в весенний сезон. Кроме того, мы видим, что в рабочие дни существует специфический паттерн около 6-7 утра и 5-6 вечера с некоторыми пиками прокатов велосипедов. Мы можем учитывать эти различные инсайты и использовать их для понимания графика частичной зависимости.
Препроцессор для моделей машинного обучения#
Поскольку мы позже используем две разные модели,
MLPRegressor и
HistGradientBoostingRegressor, мы создаем два разных
препроцессора, специфичных для каждой модели.
Препроцессор для модели нейронной сети#
Мы будем использовать QuantileTransformer масштабировать
числовые признаки и кодировать категориальные признаки с помощью
OneHotEncoder.
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, QuantileTransformer
mlp_preprocessor = ColumnTransformer(
transformers=[
("num", QuantileTransformer(n_quantiles=100), numerical_features),
("cat", OneHotEncoder(handle_unknown="ignore"), categorical_features),
]
)
mlp_preprocessor
Препроцессор для модели градиентного бустинга#
Для модели градиентного бустинга мы оставляем числовые признаки как есть и кодируем только категориальные признаки с помощью
OrdinalEncoder.
from sklearn.preprocessing import OrdinalEncoder
hgbdt_preprocessor = ColumnTransformer(
transformers=[
("cat", OrdinalEncoder(), categorical_features),
("num", "passthrough", numerical_features),
],
sparse_threshold=1,
verbose_feature_names_out=False,
).set_output(transform="pandas")
hgbdt_preprocessor
1-сторонняя частичная зависимость с разными моделями#
В этом разделе мы вычислим 1-стороннюю частичную зависимость с двумя разными моделями машинного обучения: (i) многослойный перцептрон и (ii) градиентный бустинг. С этими двумя моделями мы проиллюстрируем, как вычислять и интерпретировать как график частичной зависимости (PDP) для числовых и категориальных признаков, так и индивидуальное условное ожидание (ICE).
Многослойный перцептрон#
Давайте обучим MLPRegressor и вычислить графики частной зависимости для одной переменной.
from time import time
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
print("Training MLPRegressor...")
tic = time()
mlp_model = make_pipeline(
mlp_preprocessor,
MLPRegressor(
hidden_layer_sizes=(30, 15),
learning_rate_init=0.01,
early_stopping=True,
random_state=0,
),
)
mlp_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {mlp_model.score(X_test, y_test):.2f}")
Training MLPRegressor...
done in 0.662s
Test R2 score: 0.61
Мы настроили конвейер, используя предобработчик, который мы создали специально для нейронной сети, и настроили размер нейронной сети и скорость обучения, чтобы получить разумный компромисс между временем обучения и прогнозной производительностью на тестовом наборе.
Важно отметить, что этот табличный набор данных имеет сильно различающиеся динамические диапазоны для своих признаков. Нейронные сети обычно очень чувствительны к признакам с разными масштабами, и забывание предобработать числовые признаки приведёт к очень плохой модели.
Можно было бы достичь еще более высокой предсказательной производительности с более крупной нейронной сетью, но обучение также было бы значительно дороже.
Обратите внимание, что важно проверить, что модель достаточно точна на тестовом наборе, прежде чем строить график частной зависимости, поскольку было бы мало смысла объяснять влияние данного признака на функцию предсказания модели с плохой предсказательной способностью. В этом отношении наша модель MLP работает достаточно хорошо.
Мы построим усредненную частную зависимость.
import matplotlib.pyplot as plt
from sklearn.inspection import PartialDependenceDisplay
common_params = {
"subsample": 50,
"n_jobs": 2,
"grid_resolution": 20,
"random_state": 0,
}
print("Computing partial dependence plots...")
features_info = {
# features of interest
"features": ["temp", "humidity", "windspeed", "season", "weather", "hour"],
# type of partial dependence plot
"kind": "average",
# information regarding categorical features
"categorical_features": categorical_features,
}
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
mlp_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with an MLPRegressor"
),
fontsize=16,
)
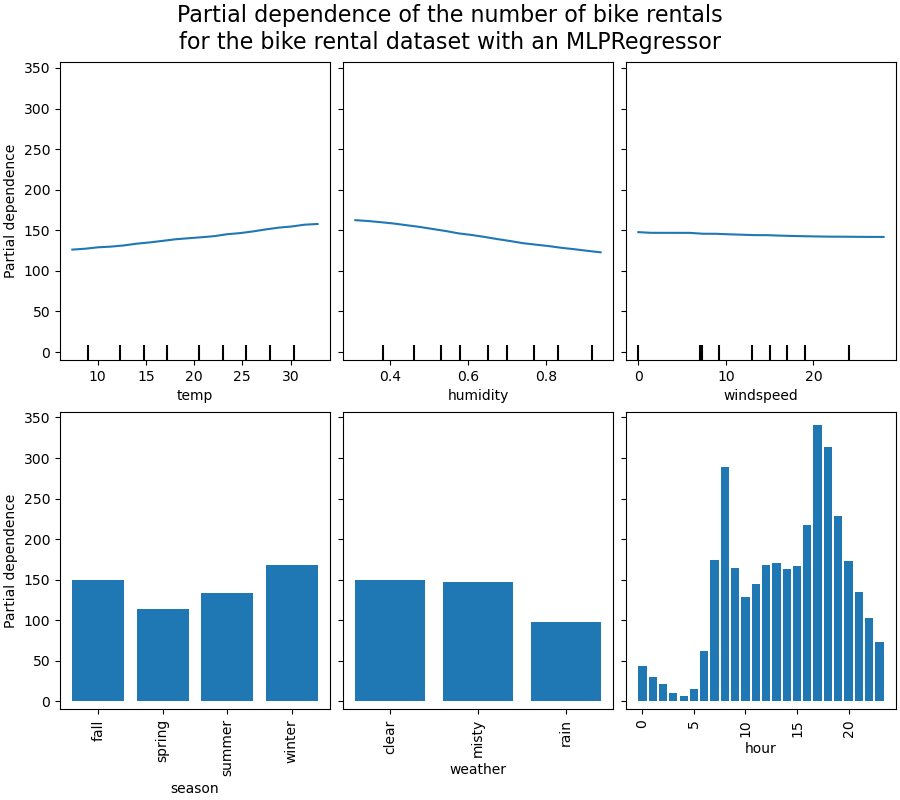
Computing partial dependence plots...
done in 0.635s
Градиентный бустинг#
Давайте теперь обучим HistGradientBoostingRegressor и вычисляем частичную зависимость по тем же признакам. Мы также используем конкретный препроцессор, созданный для этой модели.
from sklearn.ensemble import HistGradientBoostingRegressor
print("Training HistGradientBoostingRegressor...")
tic = time()
hgbdt_model = make_pipeline(
hgbdt_preprocessor,
HistGradientBoostingRegressor(
categorical_features=categorical_features,
random_state=0,
max_iter=50,
),
)
hgbdt_model.fit(X_train, y_train)
print(f"done in {time() - tic:.3f}s")
print(f"Test R2 score: {hgbdt_model.score(X_test, y_test):.2f}")
Training HistGradientBoostingRegressor...
done in 0.119s
Test R2 score: 0.62
Здесь мы использовали гиперпараметры по умолчанию для модели градиентного бустинга без какой-либо предварительной обработки, так как древовидные модели естественно устойчивы к монотонным преобразованиям числовых признаков.
Обратите внимание, что на этом табличном наборе данных градиентный бустинг на деревьях значительно быстрее обучается и точнее, чем нейронные сети. Также значительно дешевле настраивать их гиперпараметры (значения по умолчанию обычно работают хорошо, в то время как для нейронных сетей это часто не так).
Мы построим частичную зависимость для некоторых числовых и категориальных признаков.
print("Computing partial dependence plots...")
tic = time()
_, ax = plt.subplots(ncols=3, nrows=2, figsize=(9, 8), constrained_layout=True)
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with a gradient boosting"
),
fontsize=16,
)
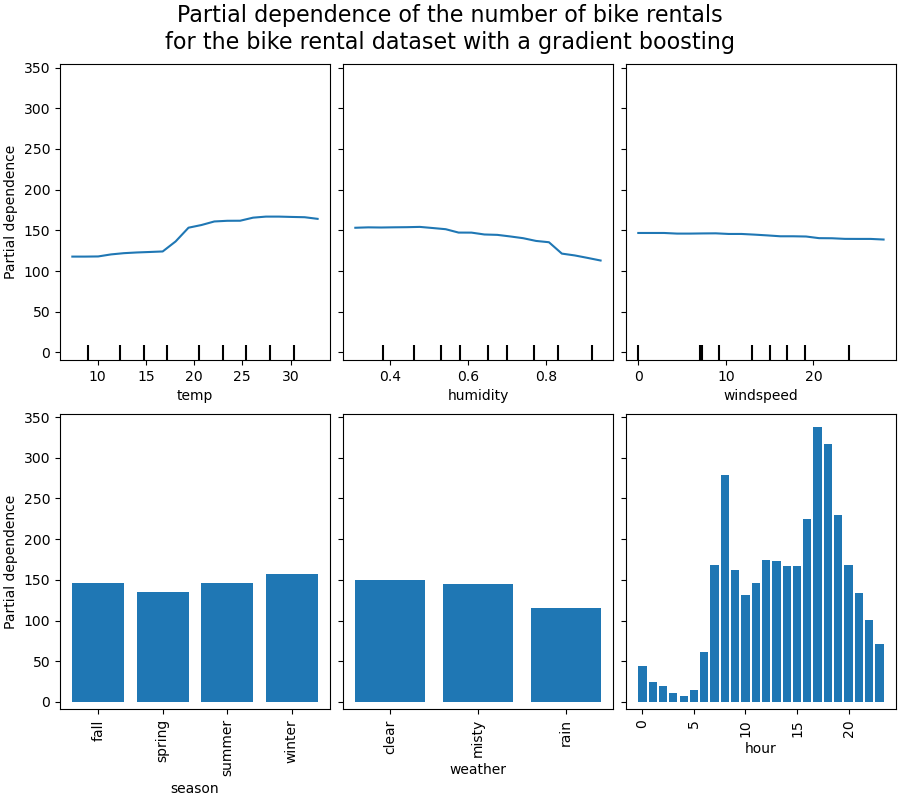
Computing partial dependence plots...
done in 1.169s
Анализ графиков#
Сначала рассмотрим частные зависимости предсказания (PDP) для числовых признаков. Для обеих моделей общая тенденция PDP температуры заключается в том, что количество прокатов велосипедов увеличивается с температурой. Можно провести аналогичный анализ, но с противоположной тенденцией для признаков влажности. Количество прокатов велосипедов уменьшается при увеличении влажности. Наконец, мы видим ту же тенденцию для признака скорости ветра. Количество прокатов велосипедов уменьшается при увеличении скорости ветра для обеих моделей. Также наблюдаем, что MLPRegressor имеет гораздо
более гладкие предсказания, чем HistGradientBoostingRegressor.
Теперь мы рассмотрим графики частных зависимостей для категориальных признаков.
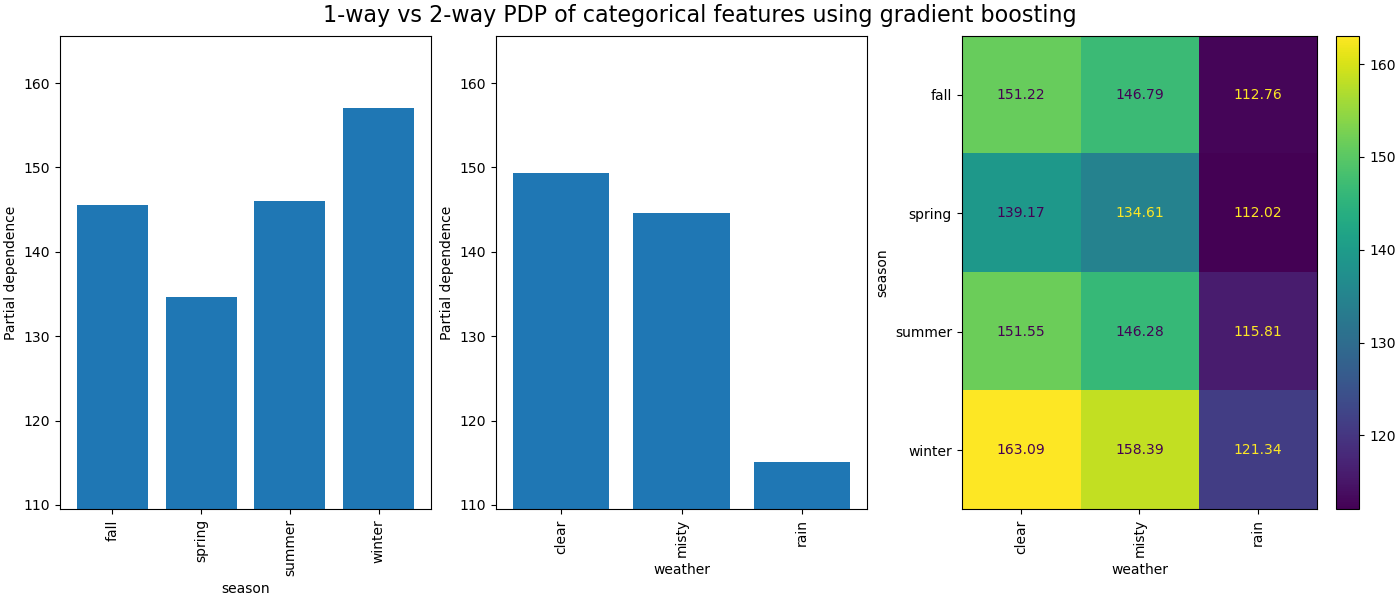
Мы наблюдаем, что весенний сезон является самым низким баром для признака сезона. Для признака погоды категория дождя является самым низким баром. Что касается признака часа, мы видим два пика около 7 утра и 6 вечера. Эти выводы соответствуют наблюдениям, сделанным ранее на наборе данных.
Однако стоит отметить, что мы создаем потенциально бессмысленные синтетические выборки, если признаки коррелированы.
ICE против PDP#
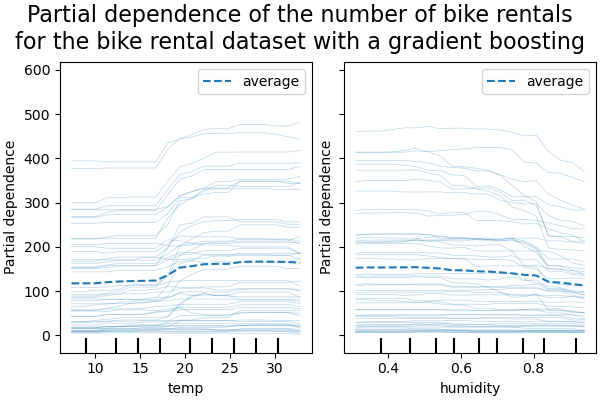
PDP — это среднее значение маргинальных эффектов признаков. Мы усредняем отклик всех образцов предоставленного набора. Таким образом, некоторые эффекты могут быть скрыты. В этом отношении можно построить каждый индивидуальный отклик. Это представление называется графиком индивидуального эффекта (ICE). На графике ниже мы строим 50 случайно выбранных ICE для признаков температуры и влажности.
print("Computing partial dependence plots and individual conditional expectation...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
"centered": True,
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)
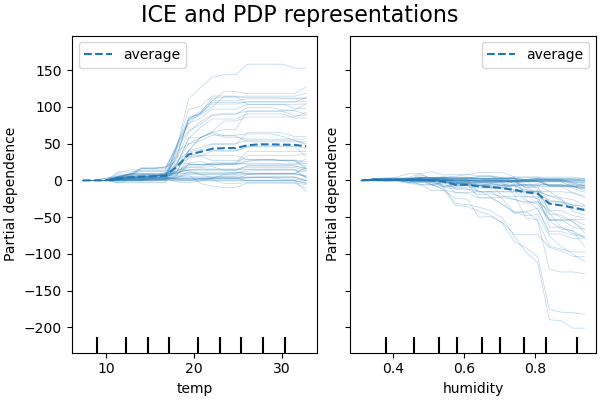
Computing partial dependence plots and individual conditional expectation...
done in 0.477s
Мы видим, что ICE для признака температуры дает нам дополнительную информацию: Некоторые линии ICE плоские, а другие показывают уменьшение зависимости для температуры выше 35 градусов Цельсия. Мы наблюдаем аналогичную картину для признака влажности: некоторые линии ICE показывают резкое уменьшение, когда влажность выше 80%.
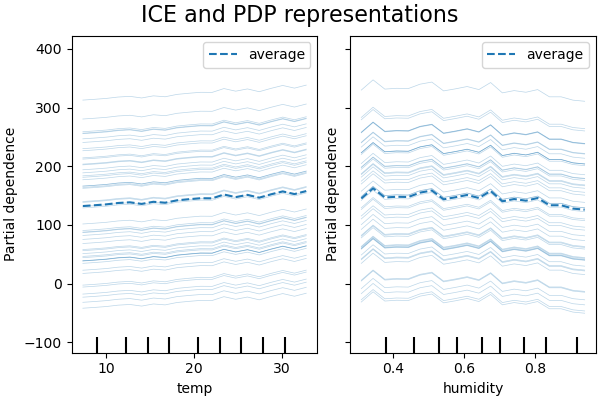
Не все линии ICE параллельны, это указывает на то, что модель находит взаимодействия между признаками. Мы можем повторить эксперимент, ограничив модель градиентного бустинга, чтобы она не использовала взаимодействия между признаками, с помощью параметра interaction_cst:
from sklearn.base import clone
interaction_cst = [[i] for i in range(X_train.shape[1])]
hgbdt_model_without_interactions = (
clone(hgbdt_model)
.set_params(histgradientboostingregressor__interaction_cst=interaction_cst)
.fit(X_train, y_train)
)
print(f"Test R2 score: {hgbdt_model_without_interactions.score(X_test, y_test):.2f}")
Test R2 score: 0.38
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info["centered"] = False
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
_ = display.figure_.suptitle("ICE and PDP representations", fontsize=16)
2D графики взаимодействий#
PDP с двумя интересующими признаками позволяют нам визуализировать взаимодействия между ними.
Однако ICE не могут быть легко построены и, следовательно, интерпретированы. Мы покажем
представление доступное в
from_estimator что представляет собой 2D
тепловую карту.
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)
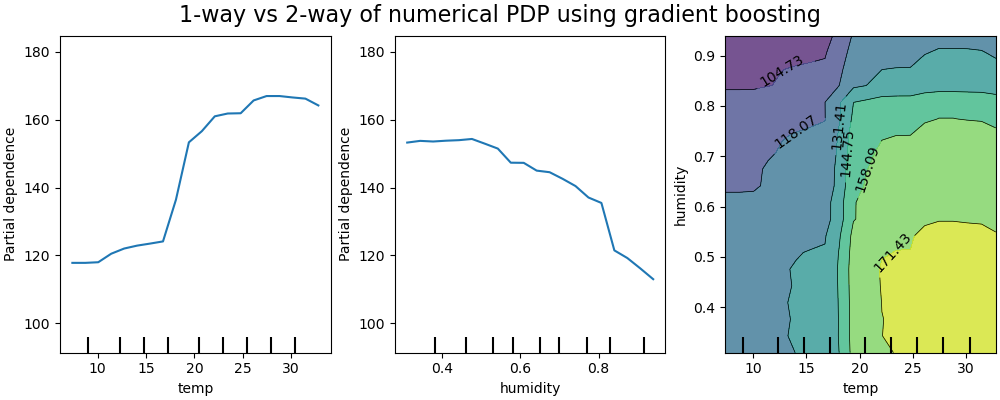
Computing partial dependence plots...
done in 7.839s
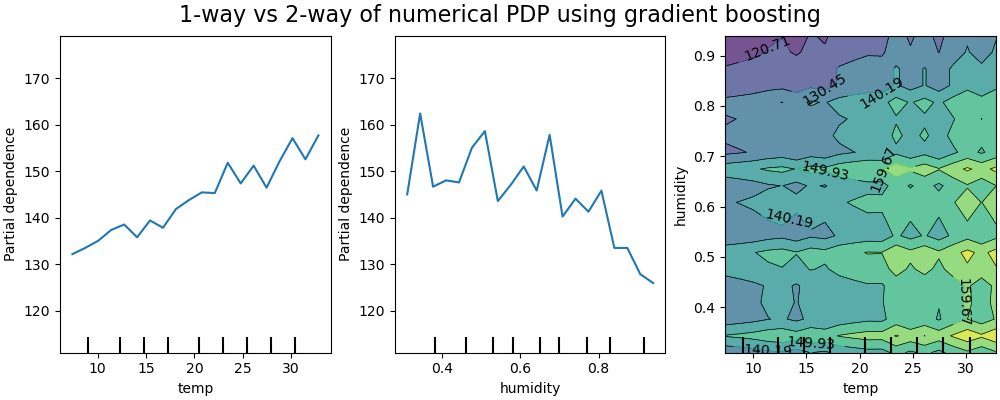
Двусторонний график частичной зависимости показывает зависимость количества прокатов велосипедов от совместных значений температуры и влажности. Мы ясно видим взаимодействие между двумя признаками. При температуре выше 20 градусов Цельсия влажность влияет на количество прокатов велосипедов, и это влияние, кажется, не зависит от температуры.
С другой стороны, для температур ниже 20 градусов Цельсия и температура, и влажность постоянно влияют на количество аренд велосипедов.
Кроме того, наклон гребня воздействия порога в 20 градусов Цельсия сильно зависит от уровня влажности: гребень крутой при сухих условиях, но гораздо более плавный при более влажных условиях выше 70% влажности.
Теперь мы сопоставляем эти результаты с теми же графиками, вычисленными для модели, ограниченной изучением предсказательной функции, которая не зависит от таких нелинейных взаимодействий признаков.
print("Computing partial dependence plots...")
features_info = {
"features": ["temp", "humidity", ("temp", "humidity")],
"kind": "average",
}
_, ax = plt.subplots(ncols=3, figsize=(10, 4), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model_without_interactions,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way of numerical PDP using gradient boosting", fontsize=16
)
Computing partial dependence plots...
done in 6.837s
1D графики частной зависимости для модели, ограниченной запретом на моделирование взаимодействий признаков, показывают локальные всплески для каждого признака в отдельности, в частности для признака «влажность». Эти всплески могут отражать ухудшенное поведение модели, которая пытается каким-то образом компенсировать запрещённые взаимодействия путём переобучения на определённых точках обучения. Отметим, что прогностическая производительность этой модели, измеренная на тестовом наборе, значительно хуже, чем у исходной, неограниченной модели.
Также обратите внимание, что количество локальных пиков, видимых на этих графиках, зависит от параметра разрешения сетки самого графика PD.
Эти локальные всплески приводят к шумному сетчатому 2D PD графику. Довольно сложно определить, есть ли взаимодействие между этими признаками из-за высокочастотных колебаний в признаке влажности. Однако можно четко увидеть, что простое эффект взаимодействия, наблюдаемый при пересечении температурой границы в 20 градусов, больше не виден для этой модели.
Частичная зависимость между категориальными признаками предоставит дискретное представление, которое можно показать в виде тепловой карты. Например, взаимодействие между сезоном, погодой и целью будет следующим:
print("Computing partial dependence plots...")
features_info = {
"features": ["season", "weather", ("season", "weather")],
"kind": "average",
"categorical_features": categorical_features,
}
_, ax = plt.subplots(ncols=3, figsize=(14, 6), constrained_layout=True)
tic = time()
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
"1-way vs 2-way PDP of categorical features using gradient boosting", fontsize=16
)
Computing partial dependence plots...
done in 0.327s
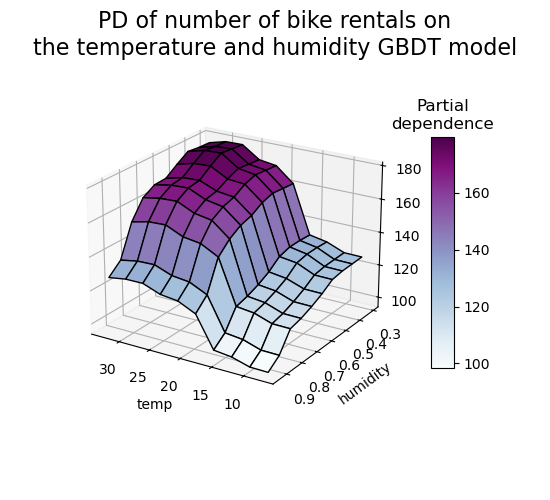
3D-представление#
Давайте построим тот же график частной зависимости для взаимодействия 2 признаков, на этот раз в 3-х измерениях.
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
import numpy as np
from sklearn.inspection import partial_dependence
fig = plt.figure(figsize=(5.5, 5))
features = ("temp", "humidity")
pdp = partial_dependence(
hgbdt_model, X_train, features=features, kind="average", grid_resolution=10
)
XX, YY = np.meshgrid(pdp["grid_values"][0], pdp["grid_values"][1])
Z = pdp.average[0].T
ax = fig.add_subplot(projection="3d")
fig.add_axes(ax)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1, cmap=plt.cm.BuPu, edgecolor="k")
ax.set_xlabel(features[0])
ax.set_ylabel(features[1])
fig.suptitle(
"PD of number of bike rentals on\nthe temperature and humidity GBDT model",
fontsize=16,
)
# pretty init view
ax.view_init(elev=22, azim=122)
clb = plt.colorbar(surf, pad=0.08, shrink=0.6, aspect=10)
clb.ax.set_title("Partial\ndependence")
plt.show()
Пользовательские точки инспекции#
Ни один из примеров до сих пор не указывает, _какие_ точки оцениваются для создания графиков частичной зависимости. По умолчанию мы используем процентили, определенные входным набором данных. В некоторых случаях может быть полезно указать точные точки, где вы хотите оценить модель. Например, если пользователь хочет проверить поведение модели на данных вне распределения или сравнить две модели, обученные на немного разных данных. custom_values параметр позволяет пользователю передавать значения, на которых они хотят оценить модель. Это переопределяет grid_resolution и
percentiles параметры. Вернемся к нашему примеру с градиентным бустингом выше, но с пользовательскими значениями
print("Computing partial dependence plots with custom evaluation values...")
tic = time()
_, ax = plt.subplots(ncols=2, figsize=(6, 4), sharey=True, constrained_layout=True)
features_info = {
"features": ["temp", "humidity"],
"kind": "both",
}
display = PartialDependenceDisplay.from_estimator(
hgbdt_model,
X_train,
**features_info,
ax=ax,
**common_params,
# we set custom values for temp feature -
# all other features are evaluated based on the data
custom_values={"temp": np.linspace(0, 40, 10)},
)
print(f"done in {time() - tic:.3f}s")
_ = display.figure_.suptitle(
(
"Partial dependence of the number of bike rentals\n"
"for the bike rental dataset with a gradient boosting"
),
fontsize=16,
)
Computing partial dependence plots with custom evaluation values...
done in 0.452s
Общее время выполнения скрипта: (0 минут 23.253 секунды)
Связанные примеры

Расширенное построение графиков с частичной зависимостью