johnson_lindenstrauss_min_dim#

sklearn.random_projection.johnson_lindenstrauss_min_dim(n_samples, *, eps=0.1)[источник]#

Найти «безопасное» количество компонентов для случайного проецирования.

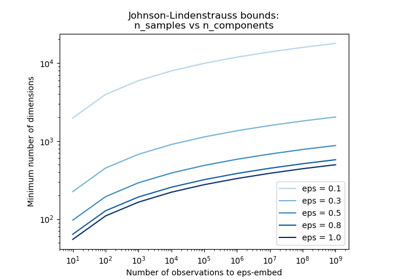
Искажение, вносимое случайной проекцией p изменяет расстояние между двумя точками только на множитель (1 +- eps) в евклидовом пространстве с высокой вероятностью. Проекция p правильно помечать.

(1 - eps) ||u - v||^2 < ||p(u) - p(v)||^2 < (1 + eps) ||u - v||^2

Где u и v — любые строки, взятые из набора данных формы (n_samples, n_features), eps находится в ]0, 1[, а p — проекция случайной гауссовской матрицей N(0, 1) формы (n_components, n_features) (или разреженной матрицей Achlioptas).

Минимальное количество компонент для гарантии eps-вложения задаётся:

n_components >= 4 log(n_samples) / (eps^2 / 2 - eps^3 / 3)

Обратите внимание, что количество измерений не зависит от исходного количества признаков, а зависит от размера набора данных: чем больше набор данных, тем выше минимальная размерность eps-вложения.

Подробнее в Руководство пользователя.

Параметры:
n_samplesint или array-like из int

Количество выборок должно быть целым числом больше 0. Если передан массив, будет вычислено безопасное количество компонентов поэлементно.

epsfloat или array-like формы (n_components,), dtype=float, по умолчанию=0.1

Максимальная скорость искажения в диапазоне (0, 1), как определено леммой Джонсона-Линденштраусса. Если задан массив, он вычислит безопасное количество компонентов поэлементно.

Возвращает:
n_componentsint или ndarray из int

Минимальное количество компонентов для гарантии с хорошей вероятностью eps-вложения с n_samples.

Ссылки

Примеры

>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(1e6, eps=0.5)
np.int64(663)

>>> johnson_lindenstrauss_min_dim(1e6, eps=[0.5, 0.1, 0.01])
array([    663,   11841, 1112658])

>>> johnson_lindenstrauss_min_dim([1e4, 1e5, 1e6], eps=0.1)
array([ 7894,  9868, 11841])