Граница Джонсона-Линденштрауса для вложения с помощью случайных проекций

The Лемма Джонсона-Линденштраусса утверждает, что любой высокоразмерный набор данных может быть случайно спроецирован в пространство меньшей размерности Евклида с контролем искажения попарных расстояний.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import sys
from time import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_20newsgroups_vectorized, load_digits
from sklearn.metrics.pairwise import euclidean_distances
from sklearn.random_projection import (
    SparseRandomProjection,
    johnson_lindenstrauss_min_dim,
)

Теоретические границы

Искажение, вносимое случайной проекцией p подтверждается тем фактом, что p определяет эпсилон-вложение с хорошей вероятностью, как определено:

\[(1 - eps) \|u - v\|^2 < \|p(u) - p(v)\|^2 < (1 + eps) \|u - v\|^2\]

Где u и v любые строки, взятые из набора данных формы (n_samples, n_features) и p является проекцией случайным гауссовым N(0, 1) матрица формы (n_components, n_features) (или разреженная матрица Ахлиоптаса).

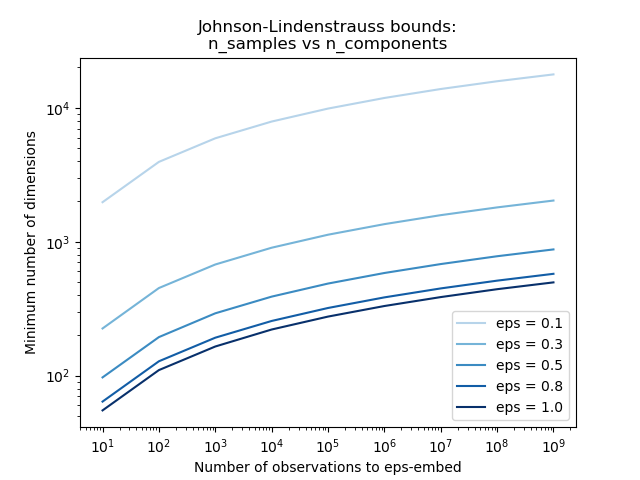
Минимальное количество компонентов, гарантирующее eps-вложение, задаётся формулой:

\[n\_components \geq 4 log(n\_samples) / (eps^2 / 2 - eps^3 / 3)\]

Вместо одного вектора коэффициентов теперь у нас есть матрица коэффициентов n_samples, минимальное количество измерений n_components увеличивается логарифмически чтобы гарантировать eps-embedding.

# range of admissible distortions
eps_range = np.linspace(0.1, 0.99, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(eps_range)))

# range of number of samples (observation) to embed
n_samples_range = np.logspace(1, 9, 9)

plt.figure()
for eps, color in zip(eps_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples_range, eps=eps)
    plt.loglog(n_samples_range, min_n_components, color=color)

plt.legend([f"eps = {eps:0.1f}" for eps in eps_range], loc="lower right")
plt.xlabel("Number of observations to eps-embed")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_samples vs n_components")
plt.show()

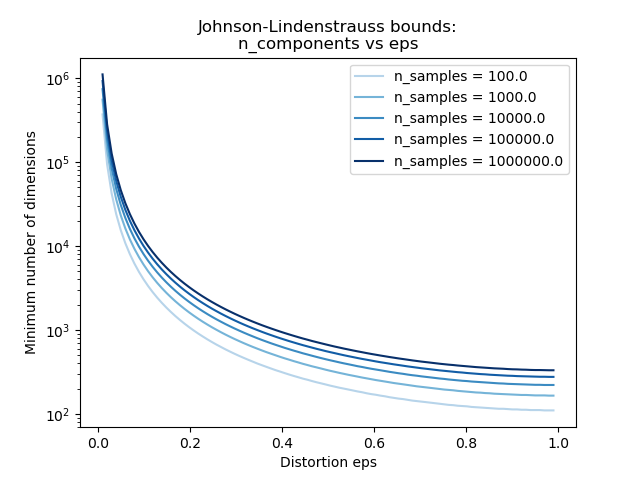
Второй график показывает, что увеличение допустимого искажения eps позволяет значительно уменьшить минимальное количество измерений n_components для заданного количества выборок n_samples

# range of admissible distortions
eps_range = np.linspace(0.01, 0.99, 100)

# range of number of samples (observation) to embed
n_samples_range = np.logspace(2, 6, 5)
colors = plt.cm.Blues(np.linspace(0.3, 1.0, len(n_samples_range)))

plt.figure()
for n_samples, color in zip(n_samples_range, colors):
    min_n_components = johnson_lindenstrauss_min_dim(n_samples, eps=eps_range)
    plt.semilogy(eps_range, min_n_components, color=color)

plt.legend([f"n_samples = {n}" for n in n_samples_range], loc="upper right")
plt.xlabel("Distortion eps")
plt.ylabel("Minimum number of dimensions")
plt.title("Johnson-Lindenstrauss bounds:\nn_components vs eps")
plt.show()

Эмпирическая проверка

Мы проверяем указанные границы на наборе текстовых документов 20 newsgroups (частоты слов TF-IDF) или на наборе данных digits:

• для набора данных 20 newsgroups около 300 документов с 100k признаков в целом проецируются с использованием разреженной случайной матрицы в меньшие евклидовы пространства с различными значениями целевого числа измерений n_components.

• для набора данных digits, некоторые 8x8 пикселей в градациях серого для 300 изображений рукописных цифр случайно проецируются в пространства с различным большим количеством измерений n_components.

Набор данных по умолчанию — 20 newsgroups. Чтобы запустить пример на наборе данных digits, передайте --use-digits-dataset аргумент командной строки для этого скрипта.

if "--use-digits-dataset" in sys.argv:
    data = load_digits().data[:300]
else:
    data = fetch_20newsgroups_vectorized().data[:300]

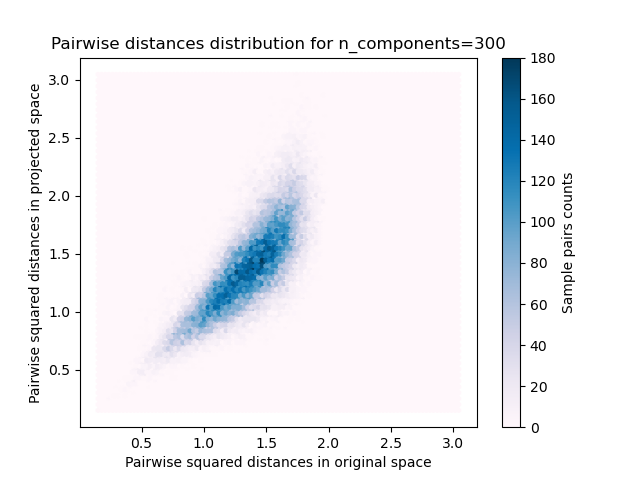
Для каждого значения n_components, мы строим график:

• 2D распределение пар выборок с попарными расстояниями в исходном и проецируемом пространствах как по оси x и y соответственно.

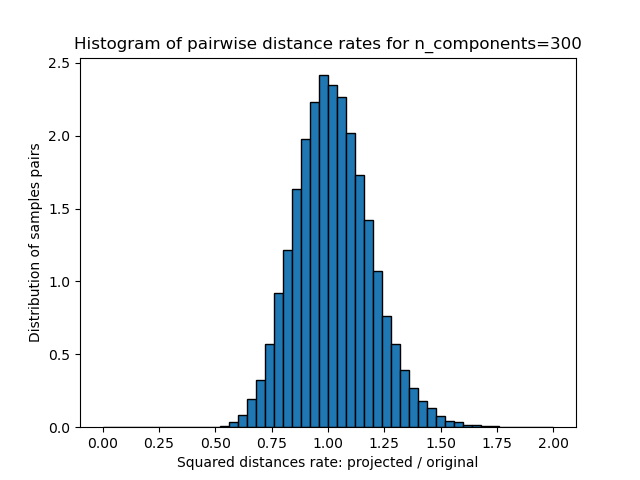
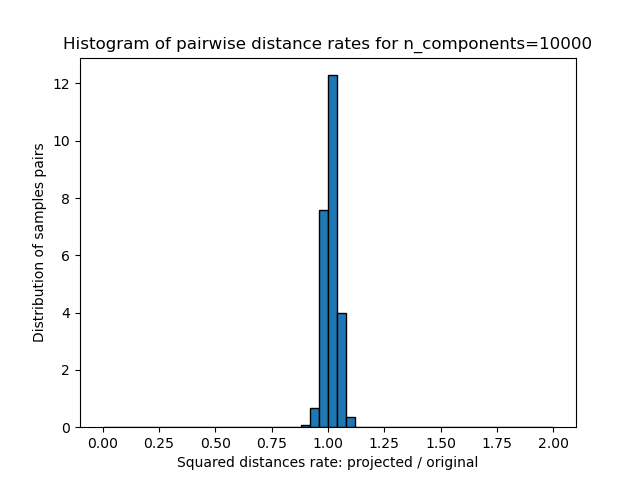
• 1D гистограмма отношения этих расстояний (спроецированных / исходных).

n_samples, n_features = data.shape
print(
    f"Embedding {n_samples} samples with dim {n_features} using various "
    "random projections"
)

n_components_range = np.array([300, 1_000, 10_000])
dists = euclidean_distances(data, squared=True).ravel()

# select only non-identical samples pairs
nonzero = dists != 0
dists = dists[nonzero]

for n_components in n_components_range:
    t0 = time()
    rp = SparseRandomProjection(n_components=n_components)
    projected_data = rp.fit_transform(data)
    print(
        f"Projected {n_samples} samples from {n_features} to {n_components} in "
        f"{time() - t0:0.3f}s"
    )
    if hasattr(rp, "components_"):
        n_bytes = rp.components_.data.nbytes
        n_bytes += rp.components_.indices.nbytes
        print(f"Random matrix with size: {n_bytes / 1e6:0.3f} MB")

    projected_dists = euclidean_distances(projected_data, squared=True).ravel()[nonzero]

    plt.figure()
    min_dist = min(projected_dists.min(), dists.min())
    max_dist = max(projected_dists.max(), dists.max())
    plt.hexbin(
        dists,
        projected_dists,
        gridsize=100,
        cmap=plt.cm.PuBu,
        extent=[min_dist, max_dist, min_dist, max_dist],
    )
    plt.xlabel("Pairwise squared distances in original space")
    plt.ylabel("Pairwise squared distances in projected space")
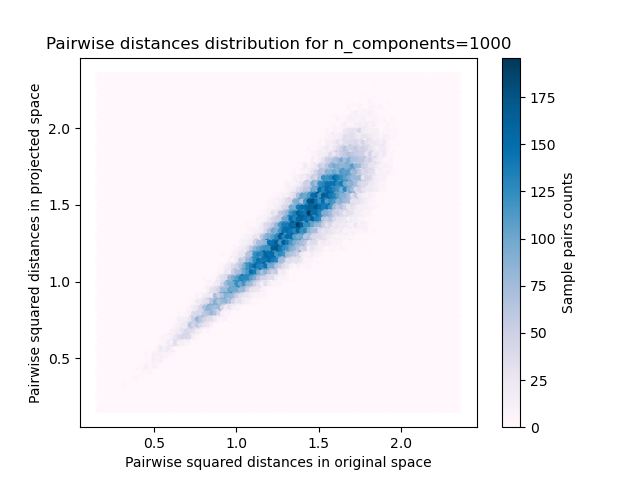
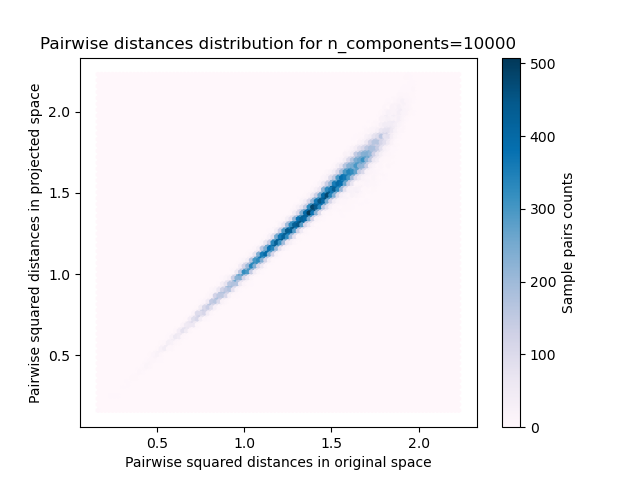
    plt.title("Pairwise distances distribution for n_components=%d" % n_components)
    cb = plt.colorbar()
    cb.set_label("Sample pairs counts")

    rates = projected_dists / dists
    print(f"Mean distances rate: {np.mean(rates):.2f} ({np.std(rates):.2f})")

    plt.figure()
    plt.hist(rates, bins=50, range=(0.0, 2.0), edgecolor="k", density=True)
    plt.xlabel("Squared distances rate: projected / original")
    plt.ylabel("Distribution of samples pairs")
    plt.title("Histogram of pairwise distance rates for n_components=%d" % n_components)

    # TODO: compute the expected value of eps and add them to the previous plot
    # as vertical lines / region

plt.show()

• 
• 
• 
• 
• 
• 

Embedding 300 samples with dim 130107 using various random projections
Projected 300 samples from 130107 to 300 in 0.227s
Random matrix with size: 1.304 MB
Mean distances rate: 1.02 (0.17)
Projected 300 samples from 130107 to 1000 in 0.750s
Random matrix with size: 4.326 MB
Mean distances rate: 1.01 (0.09)
Projected 300 samples from 130107 to 10000 in 7.567s
Random matrix with size: 43.248 MB
Mean distances rate: 1.01 (0.03)

Мы видим, что для низких значений n_components распределение широкое со многими искаженными парами и скошенное распределение (из-за жесткого ограничения нулевого соотношения слева, так как расстояния всегда положительны), в то время как для больших значений n_components искажение контролируется, и расстояния хорошо сохраняются случайной проекцией.

Замечания

Согласно лемме JL, проекция 300 выборок без значительных искажений потребует как минимум несколько тысяч измерений, независимо от количества признаков исходного набора данных.

Следовательно, использование случайных проекций на наборе данных digits, который имеет только 64 признака во входном пространстве, не имеет смысла: это не позволяет осуществить снижение размерности в данном случае.

С другой стороны, на twenty newsgroups размерность может быть уменьшена с 56,436 до 10,000 при разумном сохранении попарных расстояний.

Связанные примеры

Демонстрация алгоритма кластеризации HDBSCAN

Демонстрация алгоритма кластеризации HDBSCAN

Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap…

Обучение многообразию на рукописных цифрах: Локально линейное вложение, Isomap...

Оценка Ледойта-Вольфа против OAS оценки

Оценка Ледойта-Вольфа против OAS оценки

load_files

load_files