Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Понимание структуры дерева решений#
Структуру дерева решений можно проанализировать, чтобы получить дополнительное представление о связи между признаками и целевой переменной для прогнозирования. В этом примере мы показываем, как получить:
бинарная древовидная структура;
глубина каждого узла и является ли он листовым;
узлы, которые были достигнуты выборкой с использованием
decision_pathметод;лист, которого достиг образец с помощью метода apply;
правила, которые использовались для предсказания образца;
путь принятия решений, общий для группы выборок.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
Обучить древовидный классификатор#
Сначала мы обучаем DecisionTreeClassifier используя
load_iris набора данных.
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = DecisionTreeClassifier(max_leaf_nodes=3, random_state=0)
clf.fit(X_train, y_train)
Структура дерева#
Классификатор решений имеет атрибут под названием tree_ который позволяет получить доступ к низкоуровневым атрибутам, таким как node_count, общее количество узлов,
и max_depth, максимальная глубина дерева.
tree_.compute_node_depths() метод вычисляет глубину каждого узла в дереве. tree_ также хранит всю структуру бинарного дерева, представленную как
несколько параллельных массивов. i-й элемент каждого массива содержит информацию
о узле i. Узел 0 является корнем дерева. Некоторые массивы применяются только к листьям или разделяющим узлам. В этом случае значения узлов другого типа произвольны. Например, массивы feature и
threshold применяются только к узлам разделения. Значения для листовых узлов в этих
массивах поэтому произвольны.
Среди этих массивов у нас есть:
children_left[i]: id левого дочернего узла узлаiили -1, если листовой узелchildren_right[i]: идентификатор правого дочернего узлаiили -1, если листовой узелfeature[i]: признак, используемый для разделения узлаithreshold[i]: пороговое значение в узлеin_node_samples[i]: количество обучающих выборок, достигающих узлаiimpurity[i]: неопределенность в узлеiweighted_n_node_samples[i]: взвешенное количество обучающих образцов, достигающих узлаivalue[i, j, k]: сводка обучающих выборок, достигших узла i для выхода j и класса k (для дерева регрессии класс установлен в 1). См. ниже для получения дополнительной информации оvalue.
Используя массивы, мы можем обойти структуру дерева для вычисления различных свойств. Ниже мы вычислим глубину каждого узла и является ли он листом.
n_nodes = clf.tree_.node_count
children_left = clf.tree_.children_left
children_right = clf.tree_.children_right
feature = clf.tree_.feature
threshold = clf.tree_.threshold
values = clf.tree_.value
node_depth = np.zeros(shape=n_nodes, dtype=np.int64)
is_leaves = np.zeros(shape=n_nodes, dtype=bool)
stack = [(0, 0)] # start with the root node id (0) and its depth (0)
while len(stack) > 0:
# `pop` ensures each node is only visited once
node_id, depth = stack.pop()
node_depth[node_id] = depth
# If the left and right child of a node is not the same we have a split
# node
is_split_node = children_left[node_id] != children_right[node_id]
# If a split node, append left and right children and depth to `stack`
# so we can loop through them
if is_split_node:
stack.append((children_left[node_id], depth + 1))
stack.append((children_right[node_id], depth + 1))
else:
is_leaves[node_id] = True
print(
"The binary tree structure has {n} nodes and has "
"the following tree structure:\n".format(n=n_nodes)
)
for i in range(n_nodes):
if is_leaves[i]:
print(
"{space}node={node} is a leaf node with value={value}.".format(
space=node_depth[i] * "\t", node=i, value=np.around(values[i], 3)
)
)
else:
print(
"{space}node={node} is a split node with value={value}: "
"go to node {left} if X[:, {feature}] <= {threshold} "
"else to node {right}.".format(
space=node_depth[i] * "\t",
node=i,
left=children_left[i],
feature=feature[i],
threshold=threshold[i],
right=children_right[i],
value=np.around(values[i], 3),
)
)
The binary tree structure has 5 nodes and has the following tree structure:
node=0 is a split node with value=[[0.33 0.304 0.366]]: go to node 1 if X[:, 3] <= 0.800000011920929 else to node 2.
node=1 is a leaf node with value=[[1. 0. 0.]].
node=2 is a split node with value=[[0. 0.453 0.547]]: go to node 3 if X[:, 2] <= 4.950000047683716 else to node 4.
node=3 is a leaf node with value=[[0. 0.917 0.083]].
node=4 is a leaf node with value=[[0. 0.026 0.974]].
Для чего здесь используется массив values?#
The tree_.value массив представляет собой 3D-массив формы [n_nodes, n_classes, n_outputs] который предоставляет долю выборок, достигающих узла для каждого класса и каждого вывода. Каждый узел имеет value массив, который представляет собой долю взвешенных образцов, достигающих
этого узла для каждого выхода и класса относительно родительского узла.
Можно преобразовать это в абсолютное взвешенное количество образцов, достигающих узла,
умножив это число на tree_.weighted_n_node_samples[node_idx] для
данного узла. Обратите внимание, что веса образцов не используются в этом примере, поэтому взвешенное
количество образцов - это количество образцов, достигающих узел, потому что каждый образец
имеет вес 1 по умолчанию.
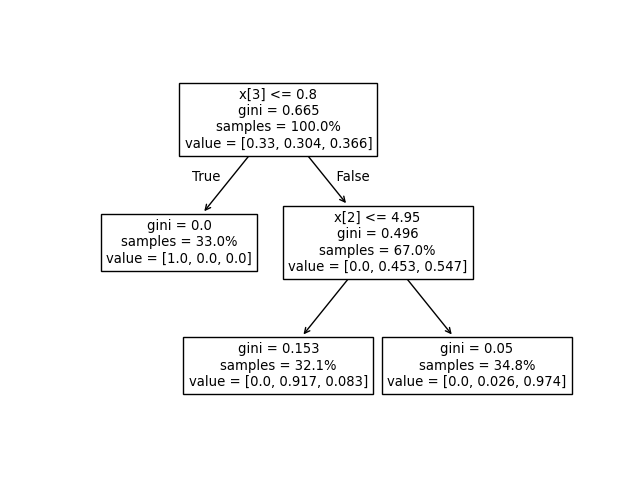
Например, в приведенном выше дереве, построенном на наборе данных iris, корневой узел имеет
value = [0.33, 0.304, 0.366] указывая, что в корневом узле 33% образцов класса 0,
30.4% образцов класса 1 и 36.6% образцов класса 2. Это можно
преобразовать в абсолютное количество образцов, умножив на количество
образцов, достигающих корневого узла, которое равно tree_.weighted_n_node_samples[0].
Тогда корневой узел имеет value = [37, 34, 41], указывая, что в корневом узле есть 37 образцов класса 0, 34 образца класса 1 и 41 образец класса 2.
При обходе дерева образцы разделяются, и в результате value массив
достигающий каждого узла изменяется. Левый дочерний узел корневого узла имеет value = [1., 0, 0]
(или value = [37, 0, 0] при преобразовании в абсолютное количество выборок)
потому что все 37 выборок в левом дочернем узле относятся к классу 0.
Примечание: в этом примере n_outputs=1, но классификатор дерева также может обрабатывать
многомерные задачи. The value массив в каждом узле будет просто двумерным
массивом.
Мы можем сравнить приведенный выше вывод с графиком дерева решений.
Здесь мы показываем пропорции образцов каждого класса, которые достигают каждого
узла, соответствующие фактическим элементам tree_.value массив.
tree.plot_tree(clf, proportion=True)
plt.show()
Путь решения#
Мы также можем получить путь принятия решений для интересующих выборок.
decision_path метод выводит индикаторную матрицу, которая позволяет нам извлекать узлы, через которые проходят интересующие выборки. Ненулевой элемент в индикаторной матрице на позиции (i, j) указывает, что выборка i проходит через узел j. Или, для одной выборки i, позиции ненулевых элементов в строке i матрицы индикаторов обозначают идентификаторы узлов, через которые проходит выборка.
Идентификаторы листьев, достигнутые интересующими выборками, можно получить с помощью
apply метод. Это возвращает массив идентификаторов узлов листьев, достигнутых каждым интересующим образцом. Используя идентификаторы листьев и
decision_path мы можем получить условия разделения, которые использовались для
предсказания одного образца или группы образцов. Сначала сделаем это для одного образца.
Обратите внимание, что node_index является разреженной матрицей.
node_indicator = clf.decision_path(X_test)
leaf_id = clf.apply(X_test)
sample_id = 0
# obtain ids of the nodes `sample_id` goes through, i.e., row `sample_id`
node_index = node_indicator.indices[
node_indicator.indptr[sample_id] : node_indicator.indptr[sample_id + 1]
]
print("Rules used to predict sample {id}:\n".format(id=sample_id))
for node_id in node_index:
# continue to the next node if it is a leaf node
if leaf_id[sample_id] == node_id:
continue
# check if value of the split feature for sample 0 is below threshold
if X_test[sample_id, feature[node_id]] <= threshold[node_id]:
threshold_sign = "<="
else:
threshold_sign = ">"
print(
"decision node {node} : (X_test[{sample}, {feature}] = {value}) "
"{inequality} {threshold})".format(
node=node_id,
sample=sample_id,
feature=feature[node_id],
value=X_test[sample_id, feature[node_id]],
inequality=threshold_sign,
threshold=threshold[node_id],
)
)
Rules used to predict sample 0:
decision node 0 : (X_test[0, 3] = 2.4) > 0.800000011920929)
decision node 2 : (X_test[0, 2] = 5.1) > 4.950000047683716)
Для группы выборок мы можем определить общие узлы, через которые проходят выборки.
sample_ids = [0, 1]
# boolean array indicating the nodes both samples go through
common_nodes = node_indicator.toarray()[sample_ids].sum(axis=0) == len(sample_ids)
# obtain node ids using position in array
common_node_id = np.arange(n_nodes)[common_nodes]
print(
"\nThe following samples {samples} share the node(s) {nodes} in the tree.".format(
samples=sample_ids, nodes=common_node_id
)
)
print("This is {prop}% of all nodes.".format(prop=100 * len(common_node_id) / n_nodes))
The following samples [0, 1] share the node(s) [0 2] in the tree.
This is 40.0% of all nodes.
Общее время выполнения скрипта: (0 минут 0.114 секунд)
Связанные примеры
Построить дендрограмму иерархической кластеризации

Пост-обрезка деревьев решений с обрезкой по стоимости сложности
Построить поверхность решений деревьев решений, обученных на наборе данных ирисов