Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Пост-обрезка деревьев решений с обрезкой по стоимости сложности#
The DecisionTreeClassifier предоставляет параметры, такие как
min_samples_leaf и max_depth чтобы предотвратить переобучение дерева. Обрезка по стоимости сложности предоставляет другой вариант для контроля размера дерева. В
DecisionTreeClassifierЭта техника обрезки параметризуется параметром сложности стоимости, ccp_alpha. Большие значения ccp_alpha
увеличить количество обрезанных узлов. Здесь мы показываем только эффект от
ccp_alpha регуляризации деревьев и как выбрать ccp_alpha
на основе валидационных оценок.
Смотрите также Минимальная обрезка по стоимости-сложности для подробностей об обрезке.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
Общая примесь листьев vs эффективные альфа-значения обрезанного дерева#
Минимальное стоимостное обрезание рекурсивно находит узел со «слабым звеном».
Слабое звено характеризуется эффективным альфа, где
узлы с наименьшим эффективным альфа обрезаются первыми. Чтобы понять,
какие значения ccp_alpha может быть уместным, scikit-learn предоставляет
DecisionTreeClassifier.cost_complexity_pruning_path который возвращает эффективные альфа-значения и соответствующие общие примеси листьев на каждом этапе процесса обрезки. По мере увеличения альфа-значения больше дерева обрезается, что увеличивает общую примесь его листьев.
X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities
На следующем графике максимальное эффективное значение альфа удалено, потому что это тривиальное дерево только с одним узлом.
fig, ax = plt.subplots()
ax.plot(ccp_alphas[:-1], impurities[:-1], marker="o", drawstyle="steps-post")
ax.set_xlabel("effective alpha")
ax.set_ylabel("total impurity of leaves")
ax.set_title("Total Impurity vs effective alpha for training set")
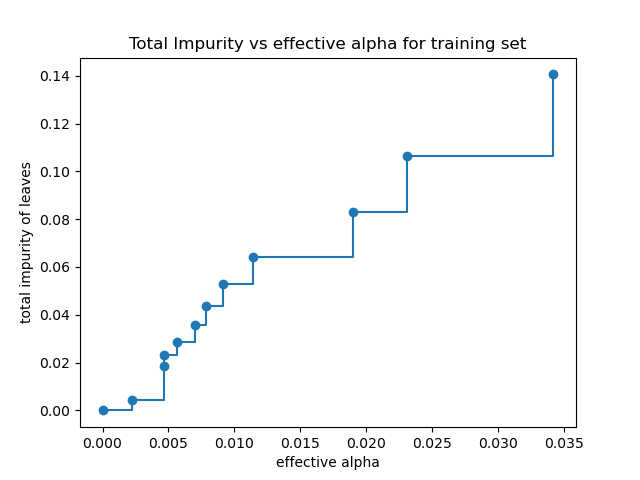
Text(0.5, 1.0, 'Total Impurity vs effective alpha for training set')
Далее мы обучаем дерево решений, используя эффективные альфы. Последнее значение
в ccp_alphas это значение alpha, которое обрезает всё дерево,
оставляя дерево, clfs[-1], с одним узлом.
clfs = []
for ccp_alpha in ccp_alphas:
clf = DecisionTreeClassifier(random_state=0, ccp_alpha=ccp_alpha)
clf.fit(X_train, y_train)
clfs.append(clf)
print(
"Number of nodes in the last tree is: {} with ccp_alpha: {}".format(
clfs[-1].tree_.node_count, ccp_alphas[-1]
)
)
Number of nodes in the last tree is: 1 with ccp_alpha: 0.3272984419327777
Для оставшейся части этого примера мы удаляем последний элемент в
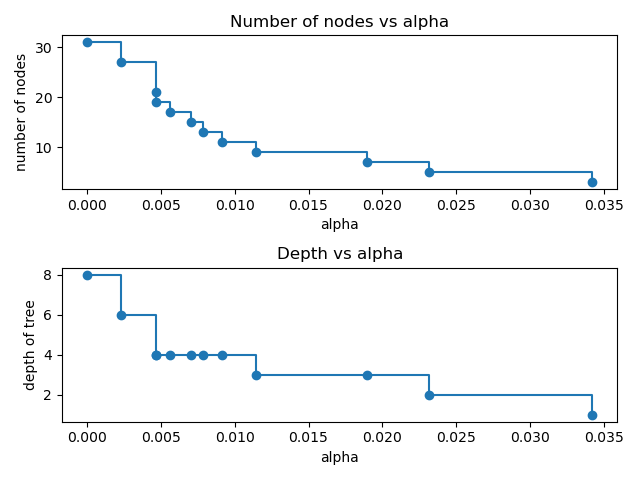
clfs и ccp_alphas, потому что это тривиальное дерево только с одним узлом. Здесь мы показываем, что количество узлов и глубина дерева уменьшаются с увеличением alpha.
clfs = clfs[:-1]
ccp_alphas = ccp_alphas[:-1]
node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
fig, ax = plt.subplots(2, 1)
ax[0].plot(ccp_alphas, node_counts, marker="o", drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[0].set_title("Number of nodes vs alpha")
ax[1].plot(ccp_alphas, depth, marker="o", drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[1].set_title("Depth vs alpha")
fig.tight_layout()
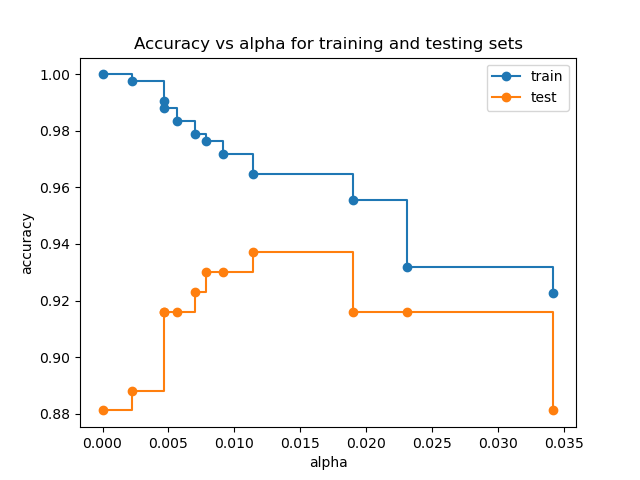
Точность в зависимости от alpha для обучающей и тестовой выборок#
Когда ccp_alpha установлен в ноль с сохранением остальных параметров по умолчанию DecisionTreeClassifier, дерево переобучается, что приводит к 100% точности обучения и 88% точности тестирования. По мере увеличения alpha больше дерева обрезается, создавая дерево решений, которое лучше обобщает. В этом примере установка ccp_alpha=0.015 максимизирует точность тестирования.
train_scores = [clf.score(X_train, y_train) for clf in clfs]
test_scores = [clf.score(X_test, y_test) for clf in clfs]
fig, ax = plt.subplots()
ax.set_xlabel("alpha")
ax.set_ylabel("accuracy")
ax.set_title("Accuracy vs alpha for training and testing sets")
ax.plot(ccp_alphas, train_scores, marker="o", label="train", drawstyle="steps-post")
ax.plot(ccp_alphas, test_scores, marker="o", label="test", drawstyle="steps-post")
ax.legend()
plt.show()
Общее время выполнения скрипта: (0 минут 0.408 секунд)
Связанные примеры
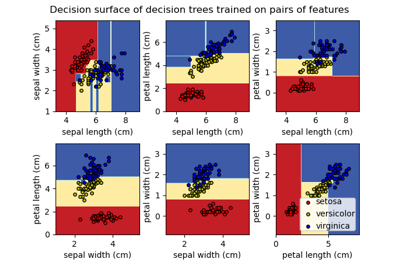
Построить поверхность решений деревьев решений, обученных на наборе данных ирисов