Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Регрессия дерева решений#
В этом примере мы демонстрируем влияние изменения максимальной глубины дерева решений на то, как оно подгоняется к данным. Мы выполняем это один раз для задачи одномерной регрессии и один раз для задачи многомерной регрессии.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Дерево решений для задачи одномерной регрессии#
Здесь мы обучаем дерево на задаче одномерной регрессии.
The деревья решений используется для подбора синусоидальной кривой с добавлением шумных наблюдений. В результате он изучает локальные линейные регрессии, аппроксимирующие синусоиду.
Мы видим, что если максимальная глубина дерева (контролируемая параметром
max_depth параметр) установлен слишком высоко, деревья решений изучают слишком мелкие детали обучающих данных и учатся на шуме, то есть переобучаются.
Создать случайный одномерный набор данных#
import numpy as np
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
Обучить модель регрессии#
параметр
from sklearn.tree import DecisionTreeRegressor
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
Predict#
Получите предсказания на тестовом наборе
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
Построить график результатов#
import matplotlib.pyplot as plt
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
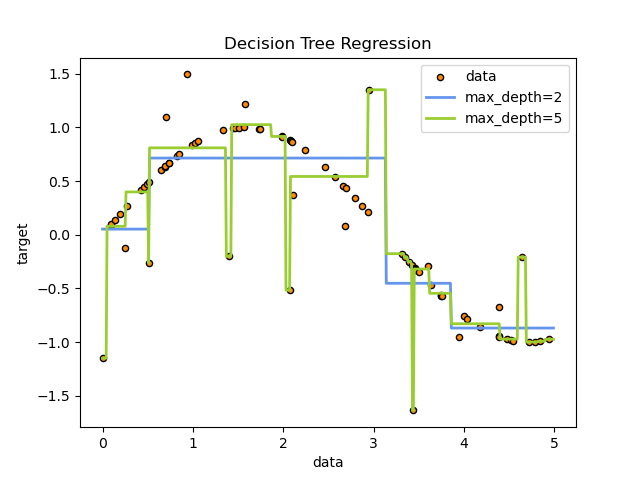
Как видите, модель с глубиной 5 (желтая) изучает детали обучающих данных до такой степени, что переобучается на шум. С другой стороны, модель с глубиной 2 (синяя) хорошо изучает основные тенденции в данных и не переобучается. В реальных случаях использования необходимо убедиться, что дерево не переобучается на обучающих данных, что можно сделать с помощью перекрестной проверки.
Регрессия дерева решений с многомерными целевыми переменными#
Здесь деревья решений
используется для одновременного предсказания зашумленных x и y наблюдения окружности
при наличии одного базового признака. В результате он изучает локальные линейные
регрессии, аппроксимирующие окружность.
Мы видим, что если максимальная глубина дерева (контролируемая параметром
max_depth параметр) установлен слишком высоко, деревья решений изучают слишком мелкие детали обучающих данных и учатся на шуме, то есть переобучаются.
Создать случайный набор данных#
Обучить модель регрессии#
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)
Predict#
Получите предсказания на тестовом наборе
X_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)
Построить график результатов#
plt.figure()
s = 25
plt.scatter(y[:, 0], y[:, 1], c="yellow", s=s, edgecolor="black", label="data")
plt.scatter(
y_1[:, 0],
y_1[:, 1],
c="cornflowerblue",
s=s,
edgecolor="black",
label="max_depth=2",
)
plt.scatter(y_2[:, 0], y_2[:, 1], c="red", s=s, edgecolor="black", label="max_depth=5")
plt.scatter(y_3[:, 0], y_3[:, 1], c="blue", s=s, edgecolor="black", label="max_depth=8")
plt.xlim([-6, 6])
plt.ylim([-6, 6])
plt.xlabel("target 1")
plt.ylabel("target 2")
plt.title("Multi-output Decision Tree Regression")
plt.legend(loc="best")
plt.show()
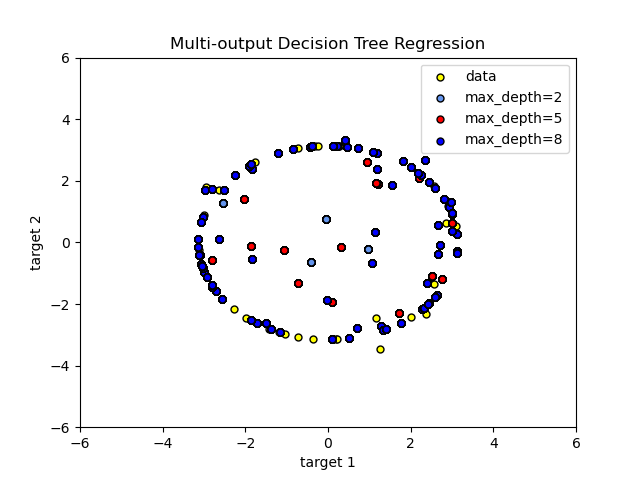
Как видите, чем выше значение max_depth, тем больше деталей данных
улавливается моделью. Однако модель также переобучается на данных и
подвержена влиянию шума.
Общее время выполнения скрипта: (0 минут 0.300 секунд)
Связанные примеры

Сравнение случайных лесов и мета-оценщика с множественным выходом

Построить поверхности решений ансамблей деревьев на наборе данных ирисов