Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Аппроксимация явного отображения признаков для RBF-ядер#
Пример, иллюстрирующий аппроксимацию карты признаков ядра RBF.
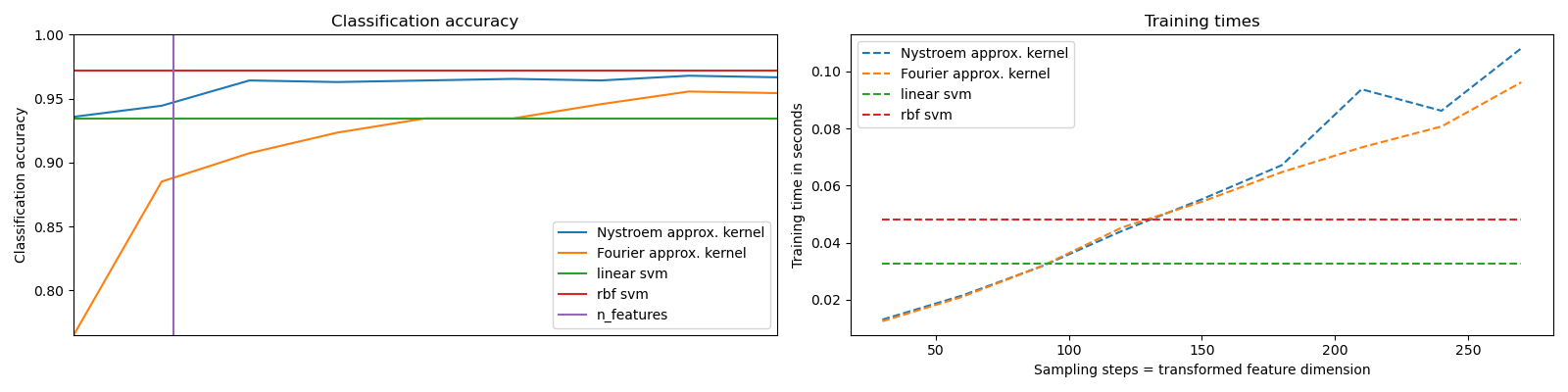
Показывает, как использовать RBFSampler и Nystroem для аппроксимации карты признаков ядра RBF для классификации с SVM на наборе данных digits. Сравниваются результаты использования линейного SVM в исходном пространстве, линейного SVM с использованием приближенных отображений и SVM с ядром. Время выполнения и точность для различного количества выборок Монте-Карло (в случае RBFSampler, который использует случайные признаки Фурье) и подмножества обучающей выборки разного размера (для Nystroem) для приближенного отображения показаны.
Обратите внимание, что набор данных здесь недостаточно велик, чтобы показать преимущества аппроксимации ядра, так как точный SVM все еще достаточно быстр.
Выборка большего количества измерений явно приводит к лучшим результатам классификации, но обходится дороже. Это означает, что существует компромисс между временем выполнения и точностью, задаваемый параметром n_components. Обратите внимание, что решение линейного SVM, а также приближенного ядерного SVM может быть значительно ускорено с использованием стохастического градиентного спуска через SGDClassifier.
Это нелегко сделать в случае ядерного SVM.
Импорт пакетов Python и наборов данных, загрузка набора данных#
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
# Standard scientific Python imports
from time import time
import matplotlib.pyplot as plt
import numpy as np
# Import datasets, classifiers and performance metrics
from sklearn import datasets, pipeline, svm
from sklearn.decomposition import PCA
from sklearn.kernel_approximation import Nystroem, RBFSampler
# The digits dataset
digits = datasets.load_digits(n_class=9)
Графики времени выполнения и точности#
Чтобы применить классификатор к этим данным, нам нужно сгладить изображение, чтобы преобразовать данные в матрицу (образцы, признаки):
n_samples = len(digits.data)
data = digits.data / 16.0
data -= data.mean(axis=0)
# We learn the digits on the first half of the digits
data_train, targets_train = (data[: n_samples // 2], digits.target[: n_samples // 2])
# Now predict the value of the digit on the second half:
data_test, targets_test = (data[n_samples // 2 :], digits.target[n_samples // 2 :])
# data_test = scaler.transform(data_test)
# Create a classifier: a support vector classifier
kernel_svm = svm.SVC(gamma=0.2)
linear_svm = svm.LinearSVC(random_state=42)
# create pipeline from kernel approximation
# and linear svm
feature_map_fourier = RBFSampler(gamma=0.2, random_state=1)
feature_map_nystroem = Nystroem(gamma=0.2, random_state=1)
fourier_approx_svm = pipeline.Pipeline(
[
("feature_map", feature_map_fourier),
("svm", svm.LinearSVC(random_state=42)),
]
)
nystroem_approx_svm = pipeline.Pipeline(
[
("feature_map", feature_map_nystroem),
("svm", svm.LinearSVC(random_state=42)),
]
)
# fit and predict using linear and kernel svm:
kernel_svm_time = time()
kernel_svm.fit(data_train, targets_train)
kernel_svm_score = kernel_svm.score(data_test, targets_test)
kernel_svm_time = time() - kernel_svm_time
linear_svm_time = time()
linear_svm.fit(data_train, targets_train)
linear_svm_score = linear_svm.score(data_test, targets_test)
linear_svm_time = time() - linear_svm_time
sample_sizes = 30 * np.arange(1, 10)
fourier_scores = []
nystroem_scores = []
fourier_times = []
nystroem_times = []
for D in sample_sizes:
fourier_approx_svm.set_params(feature_map__n_components=D)
nystroem_approx_svm.set_params(feature_map__n_components=D)
start = time()
nystroem_approx_svm.fit(data_train, targets_train)
nystroem_times.append(time() - start)
start = time()
fourier_approx_svm.fit(data_train, targets_train)
fourier_times.append(time() - start)
fourier_score = fourier_approx_svm.score(data_test, targets_test)
nystroem_score = nystroem_approx_svm.score(data_test, targets_test)
nystroem_scores.append(nystroem_score)
fourier_scores.append(fourier_score)
# plot the results:
plt.figure(figsize=(16, 4))
accuracy = plt.subplot(121)
# second y axis for timings
timescale = plt.subplot(122)
accuracy.plot(sample_sizes, nystroem_scores, label="Nystroem approx. kernel")
timescale.plot(sample_sizes, nystroem_times, "--", label="Nystroem approx. kernel")
accuracy.plot(sample_sizes, fourier_scores, label="Fourier approx. kernel")
timescale.plot(sample_sizes, fourier_times, "--", label="Fourier approx. kernel")
# horizontal lines for exact rbf and linear kernels:
accuracy.plot(
[sample_sizes[0], sample_sizes[-1]],
[linear_svm_score, linear_svm_score],
label="linear svm",
)
timescale.plot(
[sample_sizes[0], sample_sizes[-1]],
[linear_svm_time, linear_svm_time],
"--",
label="linear svm",
)
accuracy.plot(
[sample_sizes[0], sample_sizes[-1]],
[kernel_svm_score, kernel_svm_score],
label="rbf svm",
)
timescale.plot(
[sample_sizes[0], sample_sizes[-1]],
[kernel_svm_time, kernel_svm_time],
"--",
label="rbf svm",
)
# vertical line for dataset dimensionality = 64
accuracy.plot([64, 64], [0.7, 1], label="n_features")
# legends and labels
accuracy.set_title("Classification accuracy")
timescale.set_title("Training times")
accuracy.set_xlim(sample_sizes[0], sample_sizes[-1])
accuracy.set_xticks(())
accuracy.set_ylim(np.min(fourier_scores), 1)
timescale.set_xlabel("Sampling steps = transformed feature dimension")
accuracy.set_ylabel("Classification accuracy")
timescale.set_ylabel("Training time in seconds")
accuracy.legend(loc="best")
timescale.legend(loc="best")
plt.tight_layout()
plt.show()
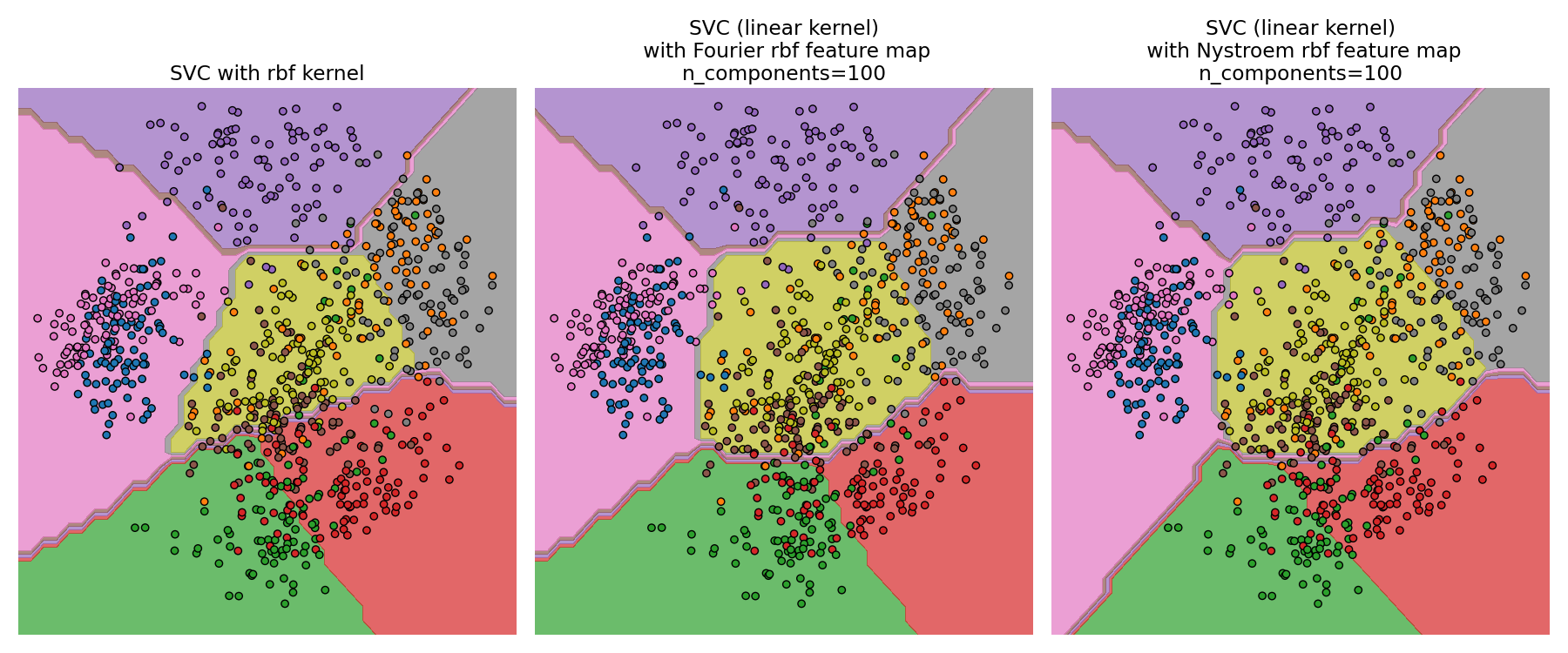
Поверхности решений SVM с RBF ядром и линейного SVM#
Второй рисунок визуализирует поверхности решений SVM с ядром RBF и
линейного SVM с приближёнными отображениями ядра.
На рисунке показаны поверхности решений классификаторов, спроецированные на
первые две главные компоненты данных. Эту визуализацию следует
воспринимать с осторожностью, так как это лишь интересный срез
поверхности решения в 64 измерениях. В частности, обратите внимание, что
точка данных (представленная точкой) не обязательно классифицируется
в регион, в котором она лежит, поскольку она может не лежать на плоскости,
которую охватывают первые две главные компоненты.
Использование RBFSampler и Nystroem подробно описан
в Аппроксимация ядра.
# visualize the decision surface, projected down to the first
# two principal components of the dataset
pca = PCA(n_components=8, random_state=42).fit(data_train)
X = pca.transform(data_train)
# Generate grid along first two principal components
multiples = np.arange(-2, 2, 0.1)
# steps along first component
first = multiples[:, np.newaxis] * pca.components_[0, :]
# steps along second component
second = multiples[:, np.newaxis] * pca.components_[1, :]
# combine
grid = first[np.newaxis, :, :] + second[:, np.newaxis, :]
flat_grid = grid.reshape(-1, data.shape[1])
# title for the plots
titles = [
"SVC with rbf kernel",
"SVC (linear kernel)\n with Fourier rbf feature map\nn_components=100",
"SVC (linear kernel)\n with Nystroem rbf feature map\nn_components=100",
]
plt.figure(figsize=(18, 7.5))
plt.rcParams.update({"font.size": 14})
# predict and plot
for i, clf in enumerate((kernel_svm, nystroem_approx_svm, fourier_approx_svm)):
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
plt.subplot(1, 3, i + 1)
Z = clf.predict(flat_grid)
# Put the result into a color plot
Z = Z.reshape(grid.shape[:-1])
levels = np.arange(10)
lv_eps = 0.01 # Adjust a mapping from calculated contour levels to color.
plt.contourf(
multiples,
multiples,
Z,
levels=levels - lv_eps,
cmap=plt.cm.tab10,
vmin=0,
vmax=10,
alpha=0.7,
)
plt.axis("off")
# Plot also the training points
plt.scatter(
X[:, 0],
X[:, 1],
c=targets_train,
cmap=plt.cm.tab10,
edgecolors=(0, 0, 0),
vmin=0,
vmax=10,
)
plt.title(titles[i])
plt.tight_layout()
plt.show()
Общее время выполнения скрипта: (0 минут 1.630 секунд)
Связанные примеры
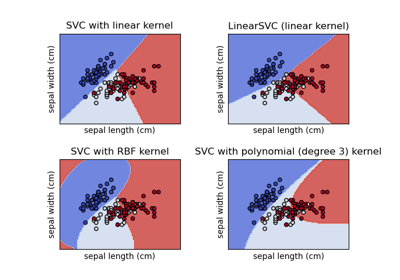
Построение различных классификаторов SVM на наборе данных iris

Масштабируемое обучение с полиномиальной аппроксимацией ядра