Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Инженерия временных признаков#
Эта записная книжка представляет различные стратегии использования временных признаков для задачи регрессии спроса на прокат велосипедов, которая сильно зависит от бизнес-циклов (дни, недели, месяцы) и годовых сезонных циклов.
В процессе мы представляем, как выполнять периодическое конструирование признаков с использованием sklearn.preprocessing.SplineTransformer класс и его
extrapolation="periodic" опция.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Исследование данных на наборе Bike Sharing Demand#
Начнем с загрузки данных из репозитория OpenML.
from sklearn.datasets import fetch_openml
bike_sharing = fetch_openml("Bike_Sharing_Demand", version=2, as_frame=True)
df = bike_sharing.frame
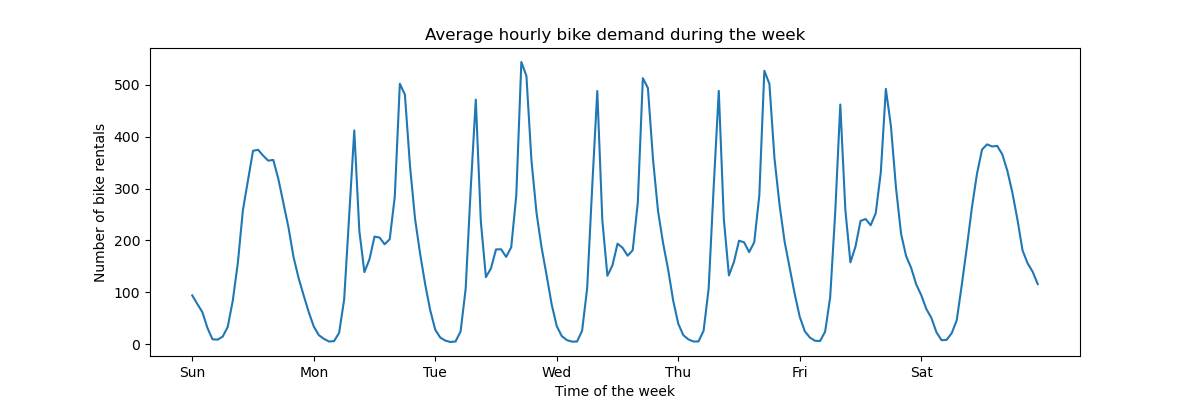
Чтобы быстро понять периодические закономерности данных, давайте посмотрим на средний спрос в час в течение недели.
Обратите внимание, что неделя начинается в воскресенье, в выходные дни. Мы можем четко различить модели поездок утром и вечером в рабочие дни и использование велосипедов для отдыха в выходные с более широким пиком спроса в середине дня:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
average_week_demand = df.groupby(["weekday", "hour"])["count"].mean()
average_week_demand.plot(ax=ax)
_ = ax.set(
title="Average hourly bike demand during the week",
xticks=[i * 24 for i in range(7)],
xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
xlabel="Time of the week",
ylabel="Number of bike rentals",
)
Целью задачи прогнозирования является абсолютное количество аренд велосипедов в почасовом разрезе:
df["count"].max()
np.int64(977)
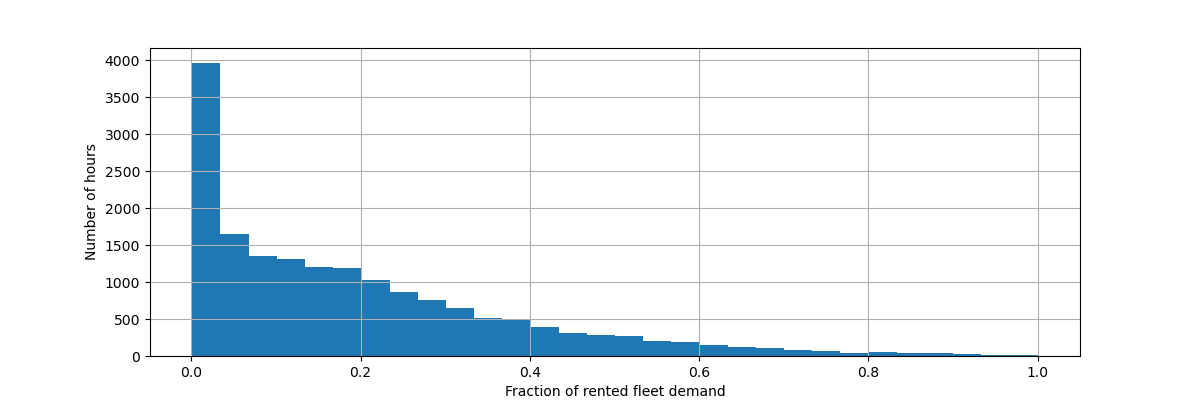
Давайте масштабируем целевую переменную (количество почасовых аренд велосипедов), чтобы предсказывать относительный спрос, чтобы средняя абсолютная ошибка интерпретировалась как доля от максимального спроса.
Примечание
Метод fit моделей, используемых в этом блокноте, минимизирует среднеквадратичную ошибку для оценки условного среднего. Однако абсолютная ошибка оценивала бы условную медиану.
Тем не менее, при представлении метрик производительности на тестовом наборе в обсуждении мы предпочитаем фокусироваться на средней абсолютной ошибке вместо (корня) средней квадратичной ошибки, поскольку её интерпретация более интуитивна. Однако обратите внимание, что в этом исследовании лучшие модели для одной метрики также являются лучшими и для другой метрики.
y = df["count"] / df["count"].max()
fig, ax = plt.subplots(figsize=(12, 4))
y.hist(bins=30, ax=ax)
_ = ax.set(
xlabel="Fraction of rented fleet demand",
ylabel="Number of hours",
)
Входной фрейм данных признаков представляет собой почасовой журнал переменных с временными аннотациями, описывающих погодные условия. Он включает как числовые, так и категориальные переменные. Обратите внимание, что временная информация уже была развернута в несколько дополнительных столбцов.
X = df.drop("count", axis="columns")
X
| сезон | год | month | hour | праздник | день недели | workingday | погода | temp | ощущаемая температура | влажность | скорость ветра | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | spring | 0 | 1 | 0 | False | 6 | False | clear | 9.84 | 14.395 | 0.81 | 0.0000 |
| 1 | spring | 0 | 1 | 1 | False | 6 | False | clear | 9.02 | 13.635 | 0.80 | 0.0000 |
| 2 | spring | 0 | 1 | 2 | False | 6 | False | clear | 9.02 | 13.635 | 0.80 | 0.0000 |
| 3 | spring | 0 | 1 | 3 | False | 6 | False | clear | 9.84 | 14.395 | 0.75 | 0.0000 |
| 4 | spring | 0 | 1 | 4 | False | 6 | False | clear | 9.84 | 14.395 | 0.75 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | spring | 1 | 12 | 19 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | spring | 1 | 12 | 20 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | spring | 1 | 12 | 21 | False | 1 | True | clear | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | spring | 1 | 12 | 22 | False | 1 | True | clear | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | spring | 1 | 12 | 23 | False | 1 | True | clear | 10.66 | 13.635 | 0.65 | 8.9981 |
17379 строк × 12 столбцов
Примечание
Если временная информация присутствовала только в виде столбца с датой или датой-временем, мы могли бы разложить её на час дня, день недели, день месяца, месяц года с помощью pandas: https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#time-date-components
Теперь мы исследуем распределение категориальных переменных, начиная с "weather":
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1419
heavy_rain 3
Name: count, dtype: int64
Поскольку есть только 3 "heavy_rain" события, мы не можем использовать эту категорию для
обучения моделей машинного обучения с перекрестной проверкой. Вместо этого мы упрощаем
представление, объединяя их в "rain" категория.
X["weather"] = (
X["weather"]
.astype(object)
.replace(to_replace="heavy_rain", value="rain")
.astype("category")
)
X["weather"].value_counts()
weather
clear 11413
misty 4544
rain 1422
Name: count, dtype: int64
Как и ожидалось, "season" переменная хорошо сбалансирована:
X["season"].value_counts()
season
fall 4496
summer 4409
spring 4242
winter 4232
Name: count, dtype: int64
Кросс-валидация на основе времени#
Поскольку набор данных представляет собой упорядоченный по времени журнал событий (почасовой спрос), мы будем использовать чувствительный ко времени разделитель перекрестной проверки для максимально реалистичной оценки нашей модели прогнозирования спроса. Мы используем разрыв в 2 дня между обучающей и тестовой частями разбиений. Мы также ограничиваем размер обучающего набора, чтобы сделать производительность фолдов CV более стабильной.
1000 тестовых точек данных должно быть достаточно для оценки производительности модели. Это представляет собой чуть меньше полутора месяцев непрерывных тестовых данных:
from sklearn.model_selection import TimeSeriesSplit
ts_cv = TimeSeriesSplit(
n_splits=5,
gap=48,
max_train_size=10000,
test_size=1000,
)
Давайте вручную проверим различные разделения, чтобы убедиться, что
TimeSeriesSplit работает, как мы ожидаем, начиная с первого разделения:
all_splits = list(ts_cv.split(X, y))
train_0, test_0 = all_splits[0]
X.iloc[test_0]
| сезон | год | month | hour | праздник | день недели | workingday | погода | temp | ощущаемая температура | влажность | скорость ветра | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12379 | лето | 1 | 6 | 0 | False | 2 | True | clear | 22.14 | 25.760 | 0.68 | 27.9993 |
| 12380 | лето | 1 | 6 | 1 | False | 2 | True | misty | 21.32 | 25.000 | 0.77 | 22.0028 |
| 12381 | лето | 1 | 6 | 2 | False | 2 | True | дождь | 21.32 | 25.000 | 0.72 | 19.9995 |
| 12382 | лето | 1 | 6 | 3 | False | 2 | True | дождь | 20.50 | 24.240 | 0.82 | 12.9980 |
| 12383 | лето | 1 | 6 | 4 | False | 2 | True | дождь | 20.50 | 24.240 | 0.82 | 12.9980 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 13374 | осень | 1 | 7 | 11 | False | 1 | True | clear | 34.44 | 40.150 | 0.53 | 15.0013 |
| 13375 | осень | 1 | 7 | 12 | False | 1 | True | clear | 34.44 | 39.395 | 0.49 | 8.9981 |
| 13376 | осень | 1 | 7 | 13 | False | 1 | True | clear | 34.44 | 39.395 | 0.49 | 19.0012 |
| 13377 | осень | 1 | 7 | 14 | False | 1 | True | clear | 36.08 | 40.910 | 0.42 | 7.0015 |
| 13378 | осень | 1 | 7 | 15 | False | 1 | True | clear | 35.26 | 40.150 | 0.47 | 16.9979 |
1000 строк × 12 столбцов
X.iloc[train_0]
| сезон | год | month | hour | праздник | день недели | workingday | погода | temp | ощущаемая температура | влажность | скорость ветра | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2331 | лето | 0 | 4 | 1 | False | 2 | True | misty | 25.42 | 31.060 | 0.50 | 6.0032 |
| 2332 | лето | 0 | 4 | 2 | False | 2 | True | misty | 24.60 | 31.060 | 0.53 | 8.9981 |
| 2333 | лето | 0 | 4 | 3 | False | 2 | True | misty | 23.78 | 27.275 | 0.56 | 8.9981 |
| 2334 | лето | 0 | 4 | 4 | False | 2 | True | misty | 22.96 | 26.515 | 0.64 | 8.9981 |
| 2335 | лето | 0 | 4 | 5 | False | 2 | True | misty | 22.14 | 25.760 | 0.68 | 8.9981 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 12326 | лето | 1 | 6 | 19 | False | 6 | False | clear | 26.24 | 31.060 | 0.36 | 11.0014 |
| 12327 | лето | 1 | 6 | 20 | False | 6 | False | clear | 25.42 | 31.060 | 0.35 | 19.0012 |
| 12328 | лето | 1 | 6 | 21 | False | 6 | False | clear | 24.60 | 31.060 | 0.40 | 7.0015 |
| 12329 | лето | 1 | 6 | 22 | False | 6 | False | clear | 23.78 | 27.275 | 0.46 | 8.9981 |
| 12330 | лето | 1 | 6 | 23 | False | 6 | False | clear | 22.96 | 26.515 | 0.52 | 7.0015 |
10000 строк × 12 столбцов
Теперь мы исследуем последнее разделение:
train_4, test_4 = all_splits[4]
X.iloc[test_4]
| сезон | год | month | hour | праздник | день недели | workingday | погода | temp | ощущаемая температура | влажность | скорость ветра | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16379 | зима | 1 | 11 | 5 | False | 2 | True | misty | 13.94 | 16.665 | 0.66 | 8.9981 |
| 16380 | зима | 1 | 11 | 6 | False | 2 | True | misty | 13.94 | 16.665 | 0.71 | 11.0014 |
| 16381 | зима | 1 | 11 | 7 | False | 2 | True | clear | 13.12 | 16.665 | 0.76 | 6.0032 |
| 16382 | зима | 1 | 11 | 8 | False | 2 | True | clear | 13.94 | 16.665 | 0.71 | 8.9981 |
| 16383 | зима | 1 | 11 | 9 | False | 2 | True | misty | 14.76 | 18.940 | 0.71 | 0.0000 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 17374 | spring | 1 | 12 | 19 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17375 | spring | 1 | 12 | 20 | False | 1 | True | misty | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17376 | spring | 1 | 12 | 21 | False | 1 | True | clear | 10.66 | 12.880 | 0.60 | 11.0014 |
| 17377 | spring | 1 | 12 | 22 | False | 1 | True | clear | 10.66 | 13.635 | 0.56 | 8.9981 |
| 17378 | spring | 1 | 12 | 23 | False | 1 | True | clear | 10.66 | 13.635 | 0.65 | 8.9981 |
1000 строк × 12 столбцов
X.iloc[train_4]
| сезон | год | month | hour | праздник | день недели | workingday | погода | temp | ощущаемая температура | влажность | скорость ветра | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6331 | зима | 0 | 9 | 9 | False | 1 | True | misty | 26.24 | 28.790 | 0.89 | 12.9980 |
| Ке и др. | зима | 0 | 9 | 10 | False | 1 | True | misty | 26.24 | 28.790 | 0.89 | 12.9980 |
| 6333 | зима | 0 | 9 | 11 | False | 1 | True | clear | 27.88 | 31.820 | 0.79 | 15.0013 |
| 6334 | зима | 0 | 9 | 12 | False | 1 | True | misty | 27.88 | 31.820 | 0.79 | 11.0014 |
| 6335 | зима | 0 | 9 | 13 | False | 1 | True | misty | 28.70 | 33.335 | 0.74 | 11.0014 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 16326 | зима | 1 | 11 | 0 | False | 0 | False | misty | 12.30 | 15.150 | 0.70 | 11.0014 |
| 16327 | зима | 1 | 11 | 1 | False | 0 | False | clear | 12.30 | 14.395 | 0.70 | 12.9980 |
| 16328 | зима | 1 | 11 | 2 | False | 0 | False | clear | 11.48 | 14.395 | 0.81 | 7.0015 |
| 16329 | зима | 1 | 11 | 3 | False | 0 | False | misty | 12.30 | 15.150 | 0.81 | 11.0014 |
| 16330 | зима | 1 | 11 | 4 | False | 0 | False | misty | 12.30 | 14.395 | 0.81 | 12.9980 |
10000 строк × 12 столбцов
Всё хорошо. Теперь мы готовы заняться прогнозным моделированием!
Градиентный бустинг#
Градиентный бустинг регрессии с деревьями решений часто достаточно гибок, чтобы эффективно обрабатывать неоднородные табличные данные со смесью категориальных и числовых признаков, если количество выборок достаточно велико.
Здесь мы используем современный
HistGradientBoostingRegressor с нативной поддержкой
категориальных признаков. Поэтому нам нужно только установить
categorical_features="from_dtype" таким образом, что признаки с категориальным типом данных считаются категориальными признаками. Для справки мы извлекаем категориальные признаки из датафрейма на основе типа данных. Внутренние деревья используют специальное правило разделения для этих признаков.
Числовые переменные не требуют предварительной обработки, и для простоты мы пробуем только гиперпараметры по умолчанию для этой модели:
from sklearn.compose import ColumnTransformer
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import cross_validate
from sklearn.pipeline import make_pipeline
gbrt = HistGradientBoostingRegressor(categorical_features="from_dtype", random_state=42)
categorical_columns = X.columns[X.dtypes == "category"]
print("Categorical features:", categorical_columns.tolist())
Categorical features: ['season', 'holiday', 'workingday', 'weather']
Давайте оценим нашу модель градиентного бустинга со средней абсолютной ошибкой относительного спроса, усредненной по нашим 5 временным кросс-валидационным разбиениям:
import numpy as np
def evaluate(model, X, y, cv, model_prop=None, model_step=None):
cv_results = cross_validate(
model,
X,
y,
cv=cv,
scoring=["neg_mean_absolute_error", "neg_root_mean_squared_error"],
return_estimator=model_prop is not None,
)
if model_prop is not None:
if model_step is not None:
values = [
getattr(m[model_step], model_prop) for m in cv_results["estimator"]
]
else:
values = [getattr(m, model_prop) for m in cv_results["estimator"]]
print(f"Mean model.{model_prop} = {np.mean(values)}")
mae = -cv_results["test_neg_mean_absolute_error"]
rmse = -cv_results["test_neg_root_mean_squared_error"]
print(
f"Mean Absolute Error: {mae.mean():.3f} +/- {mae.std():.3f}\n"
f"Root Mean Squared Error: {rmse.mean():.3f} +/- {rmse.std():.3f}"
)
evaluate(gbrt, X, y, cv=ts_cv, model_prop="n_iter_")
Mean model.n_iter_ = 100.0
Mean Absolute Error: 0.044 +/- 0.003
Root Mean Squared Error: 0.068 +/- 0.005
Мы видим, что мы установили max_iter достаточно большим, чтобы произошла ранняя остановка.
Эта модель имеет среднюю ошибку около 4–5% от максимального спроса. Это довольно хорошо для первого испытания без какой-либо настройки гиперпараметров! Нам просто нужно было сделать категориальные переменные явными. Обратите внимание, что временные признаки передаются как есть, т.е. без их обработки. Но это не является большой проблемой для моделей на основе деревьев, так как они могут изучить немонотонную связь между порядковыми входными признаками и целевой переменной.
Это не относится к моделям линейной регрессии, как мы увидим далее.
Наивная линейная регрессия#
Как обычно для линейных моделей, категориальные переменные должны быть закодированы методом one-hot. Для согласованности мы масштабируем числовые признаки до того же диапазона 0-1, используя
MinMaxScaler, хотя в данном случае это не
сильно влияет на результаты, поскольку они уже находятся в сопоставимых масштабах:
from sklearn.linear_model import RidgeCV
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder
one_hot_encoder = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
alphas = np.logspace(-6, 6, 25)
naive_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(
naive_linear_pipeline, X, y, cv=ts_cv, model_prop="alpha_", model_step="ridgecv"
)
Mean model.alpha_ = 2.7298221281347037
Mean Absolute Error: 0.142 +/- 0.014
Root Mean Squared Error: 0.184 +/- 0.020
Утвердительно видеть, что выбранный alpha_ Значение наименьшего коэффициента между 0 и 1.
Производительность неудовлетворительна: средняя ошибка составляет около 14% от максимального спроса. Это более чем в три раза выше, чем средняя ошибка модели градиентного бустинга. Можно предположить, что наивное исходное кодирование (просто масштабированное по минимуму-максимуму) периодических временных признаков может препятствовать линейной регрессионной модели должным образом использовать временную информацию: линейная регрессия не моделирует автоматически немонотонные связи между входными признаками и целевой переменной. Нелинейные члены должны быть сконструированы во входных данных.
Например, исходное числовое кодирование "hour" особенность предотвращает распознавание линейной моделью того, что увеличение часа утром с 6 до 8 должно сильно положительно влиять на количество аренд велосипедов, в то время как увеличение аналогичной величины вечером с 18 до 20 должно сильно отрицательно влиять на прогнозируемое количество аренд велосипедов.
Временные шаги как категории#
Поскольку временные признаки закодированы дискретным образом с использованием целых чисел (24 уникальных значения в признаке "часы"), мы можем решить обрабатывать их как категориальные переменные с использованием one-hot кодирования и тем самым игнорировать любые предположения, подразумеваемые упорядочиванием значений часов.
Использование one-hot кодирования для временных признаков дает линейной модели гораздо больше гибкости, так как мы вводим один дополнительный признак на каждый дискретный уровень времени.
one_hot_linear_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder=MinMaxScaler(),
),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.099 +/- 0.011
Root Mean Squared Error: 0.131 +/- 0.011
Средняя ошибка этой модели составляет 10%, что намного лучше, чем использование исходного (ординального) кодирования временного признака, подтверждая нашу интуицию о том, что модель линейной регрессии выигрывает от дополнительной гибкости, позволяющей не рассматривать прогрессию времени монотонным образом.
Однако это вводит очень большое количество новых признаков. Если бы время
дня было представлено в минутах с начала дня вместо
часов, one-hot кодирование создало бы 1440 признаков вместо 24.
Это может вызвать значительное переобучение. Чтобы избежать этого, мы можем использовать
sklearn.preprocessing.KBinsDiscretizer вместо этого для перераспределения количества уровней мелкозернистых порядковых или числовых переменных, при этом все еще получая преимущества немонотонной выразительности one-hot кодирования.
Наконец, мы также наблюдаем, что one-hot encoding полностью игнорирует порядок уровней часа, хотя это может быть интересным индуктивным смещением, которое стоит сохранить до некоторой степени. Далее мы попытаемся исследовать гладкое, немонотонное кодирование, которое локально сохраняет относительный порядок временных признаков.
Тригонометрические признаки#
В качестве первой попытки мы можем попробовать закодировать каждый из этих периодических признаков с использованием преобразования синуса и косинуса с соответствующим периодом.
Каждый порядковый временной признак преобразуется в 2 признака, которые вместе кодируют эквивалентную информацию не монотонным способом, и, что более важно, без любого скачка между первым и последним значением периодического диапазона.
from sklearn.preprocessing import FunctionTransformer
def sin_transformer(period):
return FunctionTransformer(lambda x: np.sin(x / period * 2 * np.pi))
def cos_transformer(period):
return FunctionTransformer(lambda x: np.cos(x / period * 2 * np.pi))
Давайте визуализируем эффект этого расширения признаков на некоторых синтетических данных о часах с небольшой экстраполяцией за пределы hour=23:
import pandas as pd
hour_df = pd.DataFrame(
np.arange(26).reshape(-1, 1),
columns=["hour"],
)
hour_df["hour_sin"] = sin_transformer(24).fit_transform(hour_df)["hour"]
hour_df["hour_cos"] = cos_transformer(24).fit_transform(hour_df)["hour"]
hour_df.plot(x="hour")
_ = plt.title("Trigonometric encoding for the 'hour' feature")
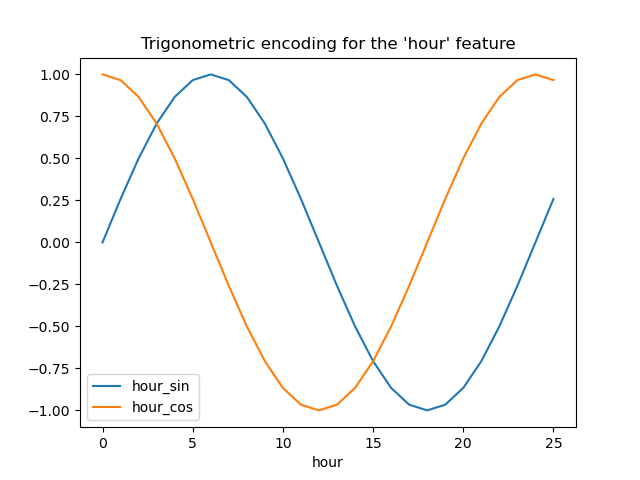
Давайте используем двумерную диаграмму рассеяния с кодировкой часов в виде цветов, чтобы лучше увидеть, как это представление отображает 24 часа суток в двумерное пространство, подобно 24-часовой версии аналоговых часов. Обратите внимание, что "25-й" час отображается обратно на 1-й час из-за периодической природы синусоидального/косинусоидального представления.
fig, ax = plt.subplots(figsize=(7, 5))
sp = ax.scatter(hour_df["hour_sin"], hour_df["hour_cos"], c=hour_df["hour"])
ax.set(
xlabel="sin(hour)",
ylabel="cos(hour)",
)
_ = fig.colorbar(sp)
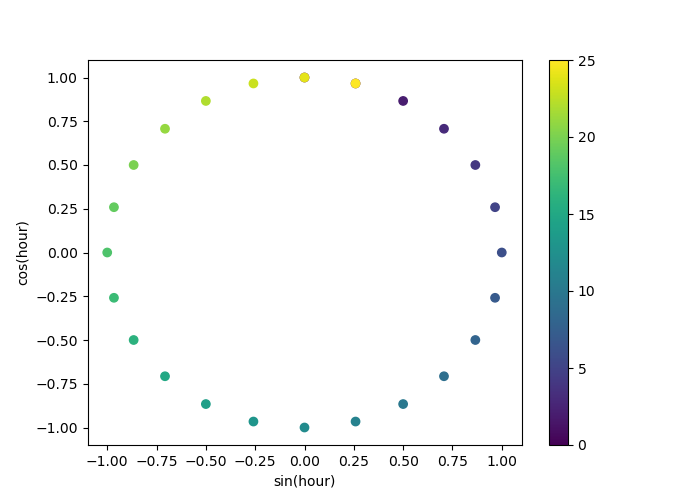
Теперь мы можем построить конвейер извлечения признаков, используя эту стратегию:
cyclic_cossin_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("month_sin", sin_transformer(12), ["month"]),
("month_cos", cos_transformer(12), ["month"]),
("weekday_sin", sin_transformer(7), ["weekday"]),
("weekday_cos", cos_transformer(7), ["weekday"]),
("hour_sin", sin_transformer(24), ["hour"]),
("hour_cos", cos_transformer(24), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_cossin_linear_pipeline = make_pipeline(
cyclic_cossin_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_cossin_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.125 +/- 0.014
Root Mean Squared Error: 0.166 +/- 0.020
Производительность нашей модели линейной регрессии с этой простой инженерией признаков немного лучше, чем при использовании исходных порядковых временных признаков, но хуже, чем при использовании one-hot кодированных временных признаков. Мы далее проанализируем возможные причины этого разочаровывающего результата в конце этой тетради.
Периодические сплайновые признаки#
Мы можем попробовать альтернативное кодирование периодических временных признаков с использованием сплайн-преобразований с достаточно большим количеством сплайнов, и как результат большим количеством расширенных признаков по сравнению с синусно-косинусным преобразованием:
from sklearn.preprocessing import SplineTransformer
def periodic_spline_transformer(period, n_splines=None, degree=3):
if n_splines is None:
n_splines = period
n_knots = n_splines + 1 # periodic and include_bias is True
return SplineTransformer(
degree=degree,
n_knots=n_knots,
knots=np.linspace(0, period, n_knots).reshape(n_knots, 1),
extrapolation="periodic",
include_bias=True,
)
Снова визуализируем эффект этого расширения признаков на некоторых синтетических данных о часах с небольшой экстраполяцией за пределы hour=23:
hour_df = pd.DataFrame(
np.linspace(0, 26, 1000).reshape(-1, 1),
columns=["hour"],
)
splines = periodic_spline_transformer(24, n_splines=12).fit_transform(hour_df)
splines_df = pd.DataFrame(
splines,
columns=[f"spline_{i}" for i in range(splines.shape[1])],
)
pd.concat([hour_df, splines_df], axis="columns").plot(x="hour", cmap=plt.cm.tab20b)
_ = plt.title("Periodic spline-based encoding for the 'hour' feature")
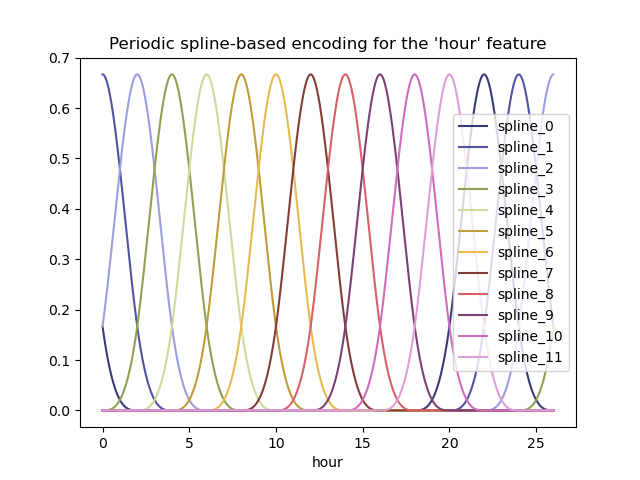
Благодаря использованию extrapolation="periodic" параметр, мы наблюдаем, что кодирование признаков остается гладким при экстраполяции за пределы полуночи.
Теперь мы можем построить прогнозный конвейер, используя эту альтернативную стратегию создания периодических признаков.
Можно использовать меньше сплайнов, чем дискретных уровней для этих порядковых значений. Это делает кодирование на основе сплайнов более эффективным, чем one-hot кодирование, сохраняя при этом большую часть выразительности:
cyclic_spline_transformer = ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("cyclic_month", periodic_spline_transformer(12, n_splines=6), ["month"]),
("cyclic_weekday", periodic_spline_transformer(7, n_splines=3), ["weekday"]),
("cyclic_hour", periodic_spline_transformer(24, n_splines=12), ["hour"]),
],
remainder=MinMaxScaler(),
)
cyclic_spline_linear_pipeline = make_pipeline(
cyclic_spline_transformer,
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_linear_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.097 +/- 0.011
Root Mean Squared Error: 0.132 +/- 0.013
Сплайн-признаки позволяют линейной модели успешно использовать периодические временные признаки и снизить ошибку с ~14% до ~10% от максимального спроса, что аналогично наблюдениям с one-hot кодированными признаками.
Качественный анализ влияния признаков на предсказания линейных моделей#
Здесь мы хотим визуализировать влияние выбора инженерии признаков на временную форму прогнозов.
Для этого мы рассматриваем произвольное разделение по времени, чтобы сравнить прогнозы на диапазоне удержанных точек данных.
naive_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
naive_linear_predictions = naive_linear_pipeline.predict(X.iloc[test_0])
one_hot_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_linear_predictions = one_hot_linear_pipeline.predict(X.iloc[test_0])
cyclic_cossin_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_cossin_linear_predictions = cyclic_cossin_linear_pipeline.predict(X.iloc[test_0])
cyclic_spline_linear_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_linear_predictions = cyclic_spline_linear_pipeline.predict(X.iloc[test_0])
Мы визуализируем эти прогнозы, увеличив последние 96 часов (4 дня) тестового набора, чтобы получить качественные инсайты:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by linear models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(naive_linear_predictions[last_hours], "x-", label="Ordinal time features")
ax.plot(
cyclic_cossin_linear_predictions[last_hours],
"x-",
label="Trigonometric time features",
)
ax.plot(
cyclic_spline_linear_predictions[last_hours],
"x-",
label="Spline-based time features",
)
ax.plot(
one_hot_linear_predictions[last_hours],
"x-",
label="One-hot time features",
)
_ = ax.legend()
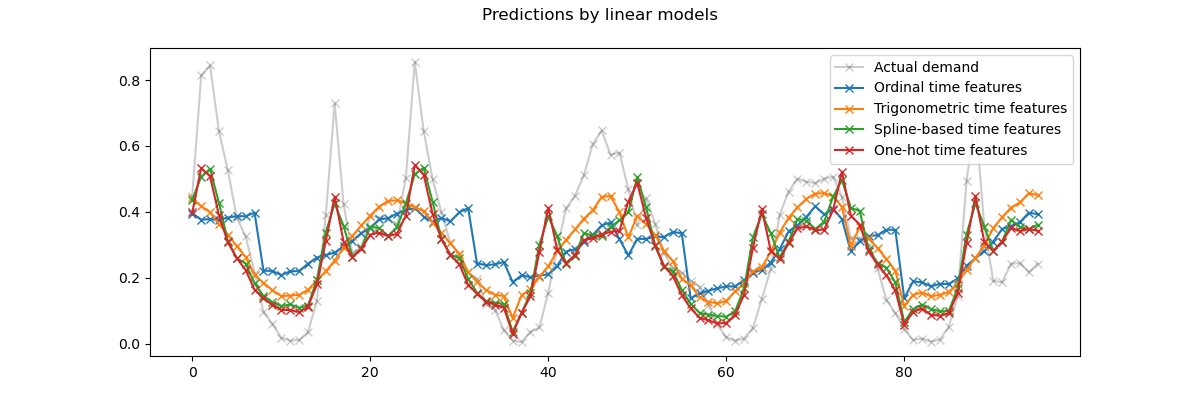
Из приведенного выше графика можно сделать следующие выводы:
The сырые порядковые временные признаки проблематичны, потому что они не учитывают естественную периодичность: мы наблюдаем большой скачок в предсказаниях в конце каждого дня, когда признак часа переходит с 23 обратно на 0. Можно ожидать аналогичных артефактов в конце каждой недели или года.
Как и ожидалось, тригонометрические признаки (синус и косинус) не имеют этих разрывов в полночь, но модель линейной регрессии не может использовать эти признаки для правильного моделирования внутридневных вариаций. Использование тригонометрических признаков для высших гармоник или дополнительных тригонометрических признаков для естественного периода с разными фазами может потенциально решить эту проблему.
the периодические сплайн-признаки решают эти две проблемы одновременно: они дают линейной модели большую выразительность, позволяя фокусироваться на определенных часах благодаря использованию 12 сплайнов. Кроме того,
extrapolation="periodic"опция обеспечивает плавное представление междуhour=23иhour=0.The one-hot закодированные признаки ведут себя аналогично периодическим сплайн-признакам, но являются более острыми: например, они могут лучше моделировать утренний пик в будние дни, поскольку этот пик длится менее часа. Однако далее мы увидим, что то, что является преимуществом для линейных моделей, не обязательно является таковым для более выразительных моделей.
Мы также можем сравнить количество признаков, извлеченных каждым конвейером инженерии признаков:
naive_linear_pipeline[:-1].transform(X).shape
(17379, 19)
one_hot_linear_pipeline[:-1].transform(X).shape
(17379, 59)
cyclic_cossin_linear_pipeline[:-1].transform(X).shape
(17379, 22)
cyclic_spline_linear_pipeline[:-1].transform(X).shape
(17379, 37)
Это подтверждает, что стратегии кодирования one-hot и сплайнов создают гораздо больше признаков для представления времени, чем альтернативы, что, в свою очередь, дает последующей линейной модели больше гибкости (степеней свободы) для избежания недообучения.
Наконец, мы наблюдаем, что ни одна из линейных моделей не может аппроксимировать реальный спрос на аренду велосипедов, особенно для пиков, которые могут быть очень резкими в часы пик в рабочие дни, но гораздо более пологими в выходные: наиболее точные линейные модели на основе сплайнов или one-hot кодирования склонны прогнозировать пики аренды велосипедов, связанные с поездками на работу, даже в выходные дни и недооценивать события, связанные с поездками на работу, в рабочие дни.
Эти систематические ошибки прогнозирования выявляют форму недообучения и могут быть объяснены отсутствием членов взаимодействия между признаками, например, 'workingday' и признаков, производных от 'hours'. Эта проблема будет рассмотрена в следующем разделе.
Моделирование парных взаимодействий со сплайнами и полиномиальными признаками#
Линейные модели не захватывают автоматически эффекты взаимодействия между входными признаками. Не помогает то, что некоторые признаки являются маргинально нелинейными, как в случае с признаками, построенными с помощью SplineTransformer (или one-hot кодирование или бининг).
Однако возможно использовать PolynomialFeatures класс на грубо
закодированных сплайнами часах для моделирования взаимодействия "рабочий день"/"часы"
явно без введения слишком большого количества новых переменных:
from sklearn.pipeline import FeatureUnion
from sklearn.preprocessing import PolynomialFeatures
hour_workday_interaction = make_pipeline(
ColumnTransformer(
[
("cyclic_hour", periodic_spline_transformer(24, n_splines=8), ["hour"]),
("workingday", FunctionTransformer(lambda x: x == "True"), ["workingday"]),
]
),
PolynomialFeatures(degree=2, interaction_only=True, include_bias=False),
)
Эти признаки затем объединяются с уже вычисленными в предыдущем конвейере на основе сплайнов. Мы можем наблюдать значительное улучшение производительности за счет явного моделирования этого попарного взаимодействия:
cyclic_spline_interactions_pipeline = make_pipeline(
FeatureUnion(
[
("marginal", cyclic_spline_transformer),
("interactions", hour_workday_interaction),
]
),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_interactions_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.078 +/- 0.009
Root Mean Squared Error: 0.104 +/- 0.009
Моделирование нелинейных взаимодействий признаков с помощью ядер#
Предыдущий анализ подчеркнул необходимость моделирования взаимодействий между
"workingday" и "hours". Другой пример такого нелинейного взаимодействия, которое мы хотели бы смоделировать, может быть влияние дождя, которое может быть неодинаковым в рабочие дни и в выходные и праздничные дни, например.
Чтобы смоделировать все такие взаимодействия, мы могли бы использовать полиномиальное разложение на все маргинальные признаки сразу после их сплайнового разложения. Однако это создаст квадратичное количество признаков, что может вызвать проблемы переобучения и вычислительной сложности.
В качестве альтернативы мы можем использовать метод Нюстрёма для вычисления приближенного разложения полиномиального ядра. Попробуем последнее:
from sklearn.kernel_approximation import Nystroem
cyclic_spline_poly_pipeline = make_pipeline(
cyclic_spline_transformer,
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(cyclic_spline_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.053 +/- 0.002
Root Mean Squared Error: 0.076 +/- 0.004
Мы наблюдаем, что эта модель почти может соперничать с производительностью градиентного бустинга деревьев со средней ошибкой около 5% от максимального спроса.
Обратите внимание, что хотя последним шагом этого конвейера является модель линейной регрессии, промежуточные шаги, такие как извлечение сплайн-признаков и аппроксимация ядра Нюстрёма, сильно нелинейны. В результате составной конвейер гораздо более выразителен, чем простая модель линейной регрессии с сырыми признаками.
Для полноты картины мы также оцениваем комбинацию one-hot кодирования и аппроксимации ядра:
one_hot_poly_pipeline = make_pipeline(
ColumnTransformer(
transformers=[
("categorical", one_hot_encoder, categorical_columns),
("one_hot_time", one_hot_encoder, ["hour", "weekday", "month"]),
],
remainder="passthrough",
),
Nystroem(kernel="poly", degree=2, n_components=300, random_state=0),
RidgeCV(alphas=alphas),
)
evaluate(one_hot_poly_pipeline, X, y, cv=ts_cv)
Mean Absolute Error: 0.082 +/- 0.006
Root Mean Squared Error: 0.111 +/- 0.011
Хотя one-hot кодированные признаки были конкурентоспособны со сплайн-базированными признаками при использовании линейных моделей, это больше не так при использовании низкоранговой аппроксимации нелинейного ядра: это можно объяснить тем, что сплайн-признаки более гладкие и позволяют аппроксимации ядра найти более выразительную решающую функцию.
Давайте теперь качественно рассмотрим прогнозы ядерных моделей и градиентного бустинга деревьев, которые должны лучше моделировать нелинейные взаимодействия между признаками:
gbrt.fit(X.iloc[train_0], y.iloc[train_0])
gbrt_predictions = gbrt.predict(X.iloc[test_0])
one_hot_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
one_hot_poly_predictions = one_hot_poly_pipeline.predict(X.iloc[test_0])
cyclic_spline_poly_pipeline.fit(X.iloc[train_0], y.iloc[train_0])
cyclic_spline_poly_predictions = cyclic_spline_poly_pipeline.predict(X.iloc[test_0])
Снова увеличим масштаб на последние 4 дня тестового набора:
last_hours = slice(-96, None)
fig, ax = plt.subplots(figsize=(12, 4))
fig.suptitle("Predictions by non-linear regression models")
ax.plot(
y.iloc[test_0].values[last_hours],
"x-",
alpha=0.2,
label="Actual demand",
color="black",
)
ax.plot(
gbrt_predictions[last_hours],
"x-",
label="Gradient Boosted Trees",
)
ax.plot(
one_hot_poly_predictions[last_hours],
"x-",
label="One-hot + polynomial kernel",
)
ax.plot(
cyclic_spline_poly_predictions[last_hours],
"x-",
label="Splines + polynomial kernel",
)
_ = ax.legend()
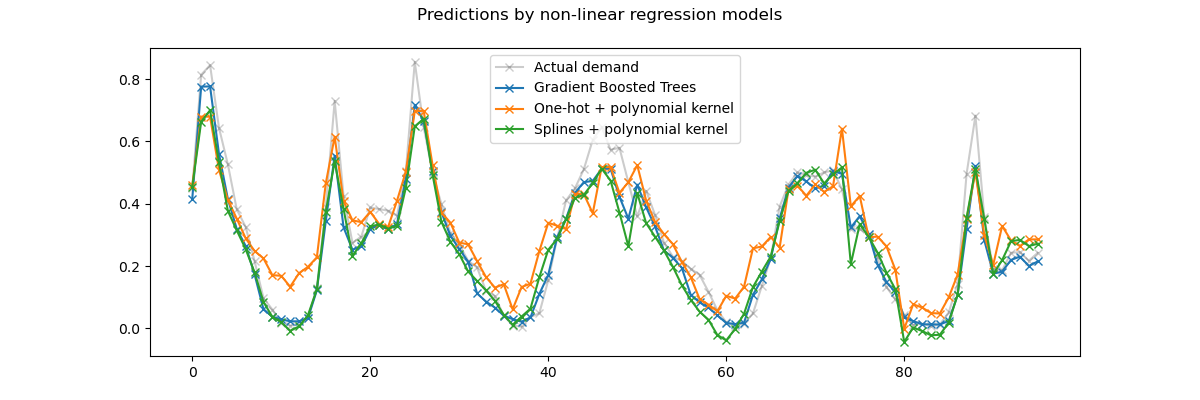
Во-первых, обратите внимание, что деревья могут естественным образом моделировать нелинейные взаимодействия признаков, поскольку по умолчанию деревья решений могут расти глубже 2 уровней.
Здесь мы можем наблюдать, что комбинации сплайновых признаков и нелинейных ядер работают довольно хорошо и могут почти соперничать с точностью деревьев градиентного бустинга для регрессии.
Напротив, one-hot кодированные временные признаки не так хорошо работают с моделью низкорангового ядра. В частности, они значительно переоценивают часы низкого спроса больше, чем конкурирующие модели.
Мы также наблюдаем, что ни одна из моделей не может успешно предсказать некоторые пиковые аренды в часы пик в рабочие дни. Возможно, для дальнейшего повышения точности прогнозов потребуется доступ к дополнительным признакам. Например, может быть полезно иметь доступ к географическому распределению парка в любой момент времени или к доле велосипедов, которые обездвижены из-за необходимости обслуживания.
Давайте наконец посмотрим более количественно на ошибки предсказания этих трех моделей, используя графики рассеяния истинного и предсказанного спроса:
from sklearn.metrics import PredictionErrorDisplay
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(13, 7), sharex=True, sharey="row")
fig.suptitle("Non-linear regression models", y=1.0)
predictions = [
one_hot_poly_predictions,
cyclic_spline_poly_predictions,
gbrt_predictions,
]
labels = [
"One hot +\npolynomial kernel",
"Splines +\npolynomial kernel",
"Gradient Boosted\nTrees",
]
plot_kinds = ["actual_vs_predicted", "residual_vs_predicted"]
for axis_idx, kind in enumerate(plot_kinds):
for ax, pred, label in zip(axes[axis_idx], predictions, labels):
disp = PredictionErrorDisplay.from_predictions(
y_true=y.iloc[test_0],
y_pred=pred,
kind=kind,
scatter_kwargs={"alpha": 0.3},
ax=ax,
)
ax.set_xticks(np.linspace(0, 1, num=5))
if axis_idx == 0:
ax.set_yticks(np.linspace(0, 1, num=5))
ax.legend(
["Best model", label],
loc="upper center",
bbox_to_anchor=(0.5, 1.3),
ncol=2,
)
ax.set_aspect("equal", adjustable="box")
plt.show()
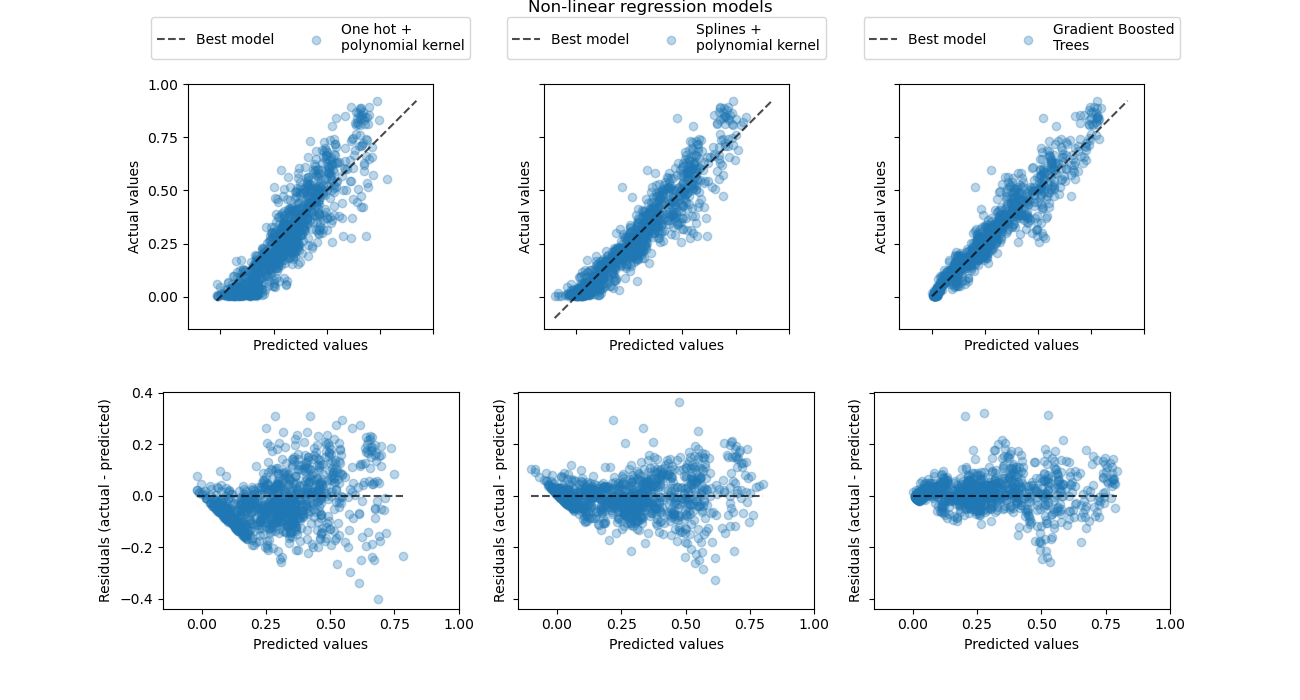
Эта визуализация подтверждает выводы, сделанные на предыдущем графике.
Все модели недооценивают события высокого спроса (часы пик в рабочие дни), но градиентный бустинг немного меньше. События низкого спроса хорошо предсказываются в среднем градиентным бустингом, в то время как конвейер полиномиальной регрессии с one-hot кодированием, кажется, систематически переоценивает спрос в этом режиме. В целом предсказания деревьев с градиентным бустингом ближе к диагонали, чем для ядерных моделей.
Заключительные замечания#
Отметим, что мы могли бы получить немного лучшие результаты для ядерных моделей,
используя больше компонентов (более высокий ранг аппроксимации ядра) за счет
более длительного времени подгонки и прогнозирования. Для больших значений n_components, производительность
признаков с one-hot кодированием могла бы даже соответствовать сплайновым
признакам.
The Nystroem + RidgeCV регрессор также можно было бы заменить на
MLPRegressor с одним или двумя скрытыми слоями
и мы получили бы довольно похожие результаты.
Набор данных, использованный в этом случае, был взят почасово. Однако циклические сплайновые признаки могли бы моделировать время в течение дня или недели очень эффективно с более мелким временным разрешением (например, с измерениями, взятыми каждую минуту вместо каждого часа) без введения большего количества признаков. One-hot кодирование временных представлений не предлагает такой гибкости.
Наконец, в этом ноутбуке мы использовали RidgeCV поскольку он очень эффективен с вычислительной точки зрения. Однако он моделирует целевую переменную как гауссовскую случайную величину с постоянной дисперсией. Для задач положительной регрессии, вероятно, использование распределения Пуассона или Гамма было бы более логичным. Этого можно достичь, используя
GridSearchCV(TweedieRegressor(power=2), param_grid({"alpha": alphas}))
вместо RidgeCV.
Общее время выполнения скрипта: (0 минут 16.827 секунд)
Связанные примеры
Лаггированные признаки для прогнозирования временных рядов
Поддержка категориальных признаков в градиентном бустинге