Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Линейный и квадратичный дискриминантный анализ с эллипсоидом ковариации#
Этот пример строит ковариационные эллипсоиды каждого класса и границу решения, изученную LinearDiscriminantAnalysis (LDA) и
QuadraticDiscriminantAnalysis (QDA).
Эллипсоиды показывают двойное стандартное отклонение для каждого класса. С LDA стандартное
отклонение одинаково для всех классов, в то время как каждый класс имеет свое стандартное
отклонение с QDA.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Генерация данных#
Сначала определим функцию для генерации синтетических данных. Она создаёт два кластера с центрами в (0, 0) и (1, 1)Каждому blob присваивается определенный класс. Дисперсия blob контролируется параметрами cov_class_1 и cov_class_2, которые являются ковариационными матрицами, используемыми при генерации выборок из гауссовских распределений.
import numpy as np
def make_data(n_samples, n_features, cov_class_1, cov_class_2, seed=0):
rng = np.random.RandomState(seed)
X = np.concatenate(
[
rng.randn(n_samples, n_features) @ cov_class_1,
rng.randn(n_samples, n_features) @ cov_class_2 + np.array([1, 1]),
]
)
y = np.concatenate([np.zeros(n_samples), np.ones(n_samples)])
return X, y
Мы генерируем три набора данных. В первом наборе данных два класса имеют одинаковую ковариационную матрицу, и эта ковариационная матрица обладает спецификой сферичности (изотропности). Второй набор данных похож на первый, но не требует, чтобы ковариация была сферической. Наконец, третий набор данных имеет несферическую ковариационную матрицу для каждого класса.
covariance = np.array([[1, 0], [0, 1]])
X_isotropic_covariance, y_isotropic_covariance = make_data(
n_samples=1_000,
n_features=2,
cov_class_1=covariance,
cov_class_2=covariance,
seed=0,
)
covariance = np.array([[0.0, -0.23], [0.83, 0.23]])
X_shared_covariance, y_shared_covariance = make_data(
n_samples=300,
n_features=2,
cov_class_1=covariance,
cov_class_2=covariance,
seed=0,
)
cov_class_1 = np.array([[0.0, -1.0], [2.5, 0.7]]) * 2.0
cov_class_2 = cov_class_1.T
X_different_covariance, y_different_covariance = make_data(
n_samples=300,
n_features=2,
cov_class_1=cov_class_1,
cov_class_2=cov_class_2,
seed=0,
)
Функции построения графиков#
Приведенный ниже код используется для построения нескольких частей информации из используемых оценщиков,
т.е., LinearDiscriminantAnalysis (LDA) и
QuadraticDiscriminantAnalysis (QDA). Отображаемая информация включает:
границу решения на основе вероятностной оценки оценщика;
диаграмма рассеяния с кругами, представляющими правильно классифицированные образцы;
диаграмма рассеяния с крестиками, представляющими неправильно классифицированные образцы;
среднее каждого класса, оцененное оценщиком, отмечено звездочкой;
оцененная ковариация, представленная эллипсом на расстоянии 2 стандартных отклонений от среднего.
import matplotlib as mpl
from matplotlib import colors
from sklearn.inspection import DecisionBoundaryDisplay
def plot_ellipse(mean, cov, color, ax):
v, w = np.linalg.eigh(cov)
u = w[0] / np.linalg.norm(w[0])
angle = np.arctan(u[1] / u[0])
angle = 180 * angle / np.pi # convert to degrees
# filled Gaussian at 2 standard deviation
ell = mpl.patches.Ellipse(
mean,
2 * v[0] ** 0.5,
2 * v[1] ** 0.5,
angle=180 + angle,
facecolor=color,
edgecolor="black",
linewidth=2,
)
ell.set_clip_box(ax.bbox)
ell.set_alpha(0.4)
ax.add_artist(ell)
def plot_result(estimator, X, y, ax):
cmap = colors.ListedColormap(["tab:red", "tab:blue"])
DecisionBoundaryDisplay.from_estimator(
estimator,
X,
response_method="predict_proba",
plot_method="pcolormesh",
ax=ax,
cmap="RdBu",
alpha=0.3,
)
DecisionBoundaryDisplay.from_estimator(
estimator,
X,
response_method="predict_proba",
plot_method="contour",
ax=ax,
alpha=1.0,
levels=[0.5],
)
y_pred = estimator.predict(X)
X_right, y_right = X[y == y_pred], y[y == y_pred]
X_wrong, y_wrong = X[y != y_pred], y[y != y_pred]
ax.scatter(X_right[:, 0], X_right[:, 1], c=y_right, s=20, cmap=cmap, alpha=0.5)
ax.scatter(
X_wrong[:, 0],
X_wrong[:, 1],
c=y_wrong,
s=30,
cmap=cmap,
alpha=0.9,
marker="x",
)
ax.scatter(
estimator.means_[:, 0],
estimator.means_[:, 1],
c="yellow",
s=200,
marker="*",
edgecolor="black",
)
if isinstance(estimator, LinearDiscriminantAnalysis):
covariance = [estimator.covariance_] * 2
else:
covariance = estimator.covariance_
plot_ellipse(estimator.means_[0], covariance[0], "tab:red", ax)
plot_ellipse(estimator.means_[1], covariance[1], "tab:blue", ax)
ax.set_box_aspect(1)
ax.spines["top"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
ax.spines["right"].set_visible(False)
ax.set(xticks=[], yticks=[])
Сравнение LDA и QDA#
Мы сравниваем два оценщика LDA и QDA на всех трех наборах данных.
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import (
LinearDiscriminantAnalysis,
QuadraticDiscriminantAnalysis,
)
fig, axs = plt.subplots(nrows=3, ncols=2, sharex="row", sharey="row", figsize=(8, 12))
lda = LinearDiscriminantAnalysis(solver="svd", store_covariance=True)
qda = QuadraticDiscriminantAnalysis(solver="svd", store_covariance=True)
for ax_row, X, y in zip(
axs,
(X_isotropic_covariance, X_shared_covariance, X_different_covariance),
(y_isotropic_covariance, y_shared_covariance, y_different_covariance),
):
lda.fit(X, y)
plot_result(lda, X, y, ax_row[0])
qda.fit(X, y)
plot_result(qda, X, y, ax_row[1])
axs[0, 0].set_title("Linear Discriminant Analysis")
axs[0, 0].set_ylabel("Data with fixed and spherical covariance")
axs[1, 0].set_ylabel("Data with fixed covariance")
axs[0, 1].set_title("Quadratic Discriminant Analysis")
axs[2, 0].set_ylabel("Data with varying covariances")
fig.suptitle(
"Linear Discriminant Analysis vs Quadratic Discriminant Analysis",
y=0.94,
fontsize=15,
)
plt.show()
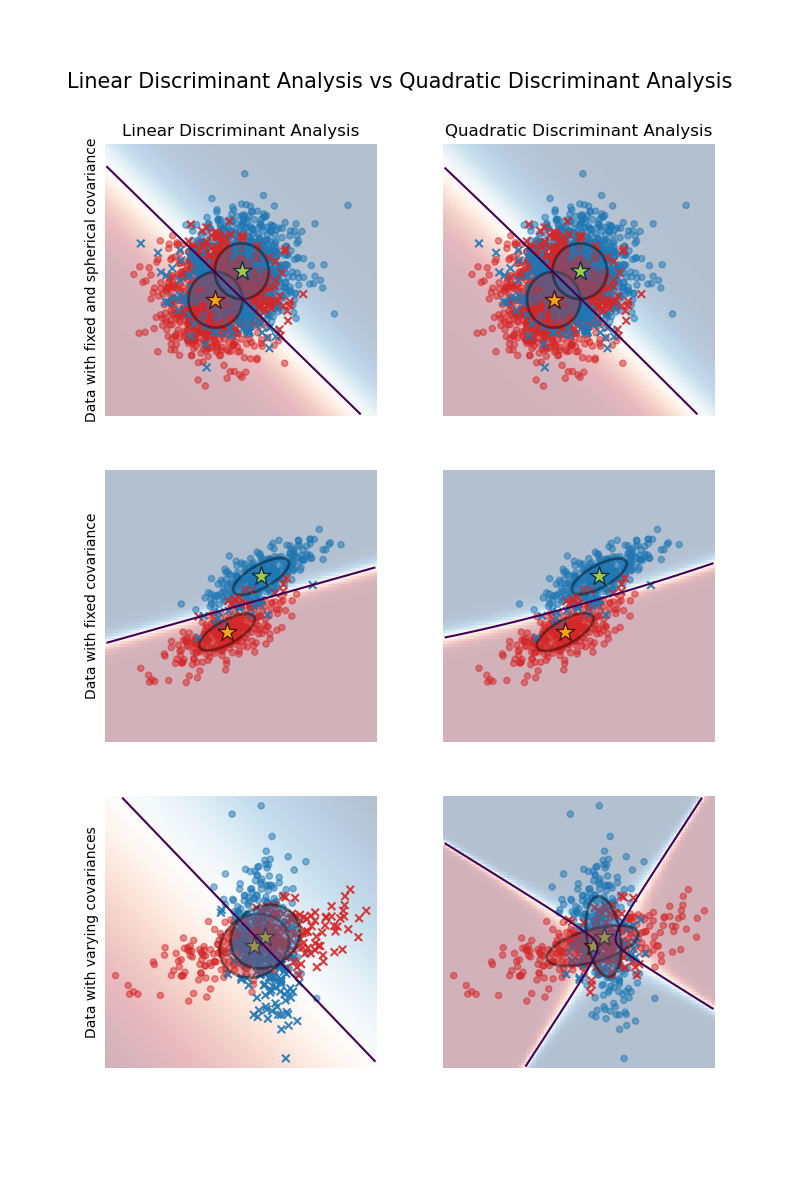
Первое важное замечание: LDA и QDA эквивалентны для первого и второго наборов данных. Действительно, основное различие в том, что LDA предполагает, что ковариационная матрица каждого класса одинакова, а QDA оценивает ковариационную матрицу для каждого класса. Поскольку в этих случаях процесс генерации данных имеет одинаковую ковариационную матрицу для обоих классов, QDA оценивает две ковариационные матрицы, которые (почти) равны и, следовательно, эквивалентны ковариационной матрице, оцененной LDA.
В первом наборе данных ковариационная матрица, используемая для генерации данных, является сферической, что приводит к дискриминантной границе, совпадающей с перпендикулярной биссектрисой между двумя средними. Это уже не так для второго набора данных. Дискриминантная граница проходит только через середину двух средних.
Наконец, в третьем наборе данных мы наблюдаем реальную разницу между LDA и QDA. QDA подгоняет две ковариационные матрицы и предоставляет нелинейную дискриминантную границу, тогда как LDA недообучается, поскольку предполагает, что оба класса используют одну ковариационную матрицу.
Общее время выполнения скрипта: (0 минут 0.482 секунды)
Связанные примеры
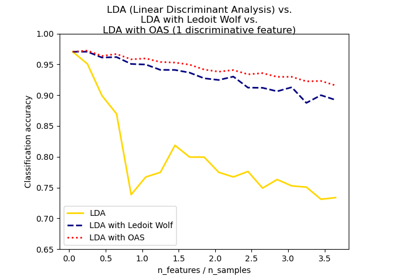
Нормальный, Ledoit-Wolf и OAS линейный дискриминантный анализ для классификации