Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Сравнение LDA и PCA 2D проекции набора данных Iris#
Набор данных Iris представляет 3 вида цветов ириса (Setosa, Versicolour и Virginica) с 4 атрибутами: длина чашелистика, ширина чашелистика, длина лепестка и ширина лепестка.
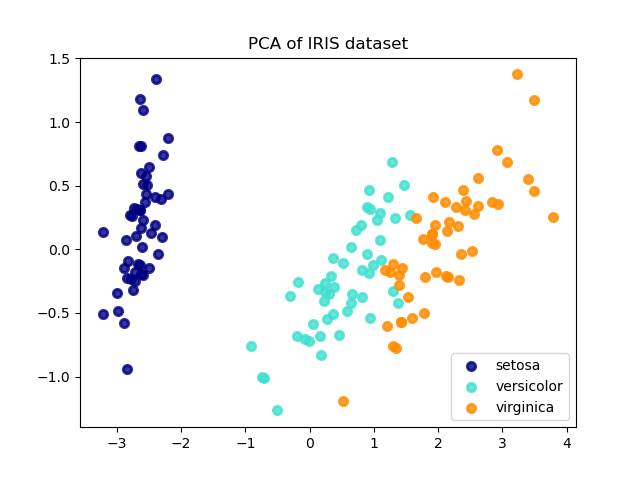
Метод главных компонент (PCA), применённый к этим данным, определяет комбинацию атрибутов (главные компоненты или направления в пространстве признаков), которые объясняют наибольшую дисперсию в данных. Здесь мы отображаем различные образцы на первых двух главных компонентах.
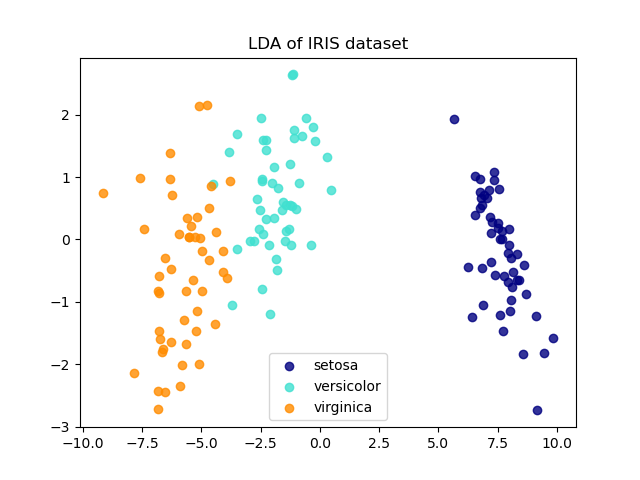
Линейный дискриминантный анализ (LDA) пытается идентифицировать атрибуты, которые объясняют наибольшую дисперсию между классами. В частности, LDA, в отличие от PCA, является контролируемым методом, использующим известные метки классов.
explained variance ratio (first two components): [0.92461872 0.05306648]
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
pca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)
lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
# Percentage of variance explained for each components
print(
"explained variance ratio (first two components): %s"
% str(pca.explained_variance_ratio_)
)
plt.figure()
colors = ["navy", "turquoise", "darkorange"]
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(
X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=0.8, lw=lw, label=target_name
)
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("PCA of IRIS dataset")
plt.figure()
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(
X_r2[y == i, 0], X_r2[y == i, 1], alpha=0.8, color=color, label=target_name
)
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.title("LDA of IRIS dataset")
plt.show()
Общее время выполнения скрипта: (0 минут 0.174 секунд)
Связанные примеры
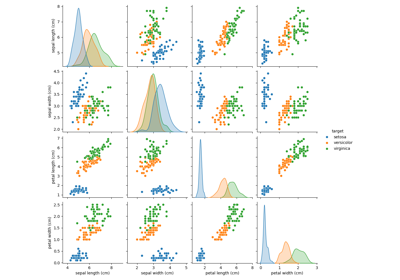
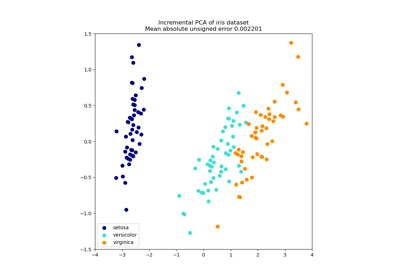
Анализ главных компонент (PCA) на наборе данных Iris
Снижение размерности с помощью анализа компонентов соседства
Построить поверхность решений деревьев решений, обученных на наборе данных ирисов