Рабочая характеристика приёмника (ROC) с перекрёстной проверкой

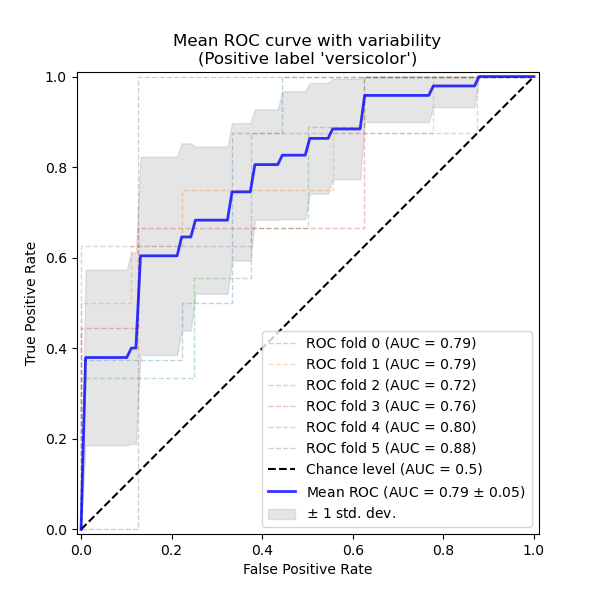
В этом примере показано, как оценить и визуализировать дисперсию метрики Receiver Operating Characteristic (ROC) с использованием перекрестной проверки.

Кривые ROC обычно имеют истинно положительную частоту (TPR) на оси Y и ложноположительную частоту (FPR) на оси X. Это означает, что верхний левый угол графика является «идеальной» точкой — FPR равен нулю, а TPR равен единице. Это не очень реалистично, но означает, что большая площадь под кривой (AUC) обычно лучше. «Крутизна» кривых ROC также важна, поскольку идеально максимизировать TPR, минимизируя FPR.

Этот пример показывает ROC-отклик различных наборов данных, созданных с помощью K-кратной перекрестной проверки. Используя все эти кривые, можно вычислить среднее значение AUC и увидеть дисперсию кривой, когда обучающая выборка разбивается на различные подмножества. Это примерно показывает, как выход классификатора зависит от изменений в обучающих данных и насколько различны разбиения, сгенерированные K-кратной перекрестной проверкой.

Примечание

См. Многоклассовая рабочая характеристика приемника (ROC) для дополнения текущего примера, объясняющего стратегии усреднения для обобщения метрик для многоклассовых классификаторов.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Загрузка и подготовка данных

Мы импортируем Набор данных о растениях ириса который содержит 3 класса, каждый из которых соответствует типу растения ирис. Один класс линейно отделим от двух других; последние не линейно разделимы друг от друга.

Далее мы бинаризируем набор данных, удалив класс 'virginica' (class_id=2). Это означает, что класс "versicolor" (class_id=1) считается положительным классом, а "setosa" — отрицательным классом (class_id=0).

import numpy as np

from sklearn.datasets import load_iris

iris = load_iris()
target_names = iris.target_names
X, y = iris.data, iris.target
X, y = X[y != 2], y[y != 2]
n_samples, n_features = X.shape

Мы также добавляем шумовые признаки, чтобы усложнить задачу.

random_state = np.random.RandomState(0)
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)

Классификация и ROC-анализ

Здесь мы запускаем cross_validate на SVC классификатор, затем используйте вычисленные результаты перекрестной проверки для построения ROC-кривых по фолдам. Обратите внимание, что базовый уровень для определения уровня случайности (пунктирная ROC-кривая) — это классификатор, который всегда предсказывает наиболее частый класс.

import matplotlib.pyplot as plt

from sklearn import svm
from sklearn.metrics import RocCurveDisplay, auc
from sklearn.model_selection import StratifiedKFold, cross_validate

n_splits = 6
cv = StratifiedKFold(n_splits=n_splits)
classifier = svm.SVC(kernel="linear", probability=True, random_state=random_state)
cv_results = cross_validate(
    classifier, X, y, cv=cv, return_estimator=True, return_indices=True
)

prop_cycle = plt.rcParams["axes.prop_cycle"]
colors = prop_cycle.by_key()["color"]
curve_kwargs_list = [
    dict(alpha=0.3, lw=1, color=colors[fold % len(colors)]) for fold in range(n_splits)
]
names = [f"ROC fold {idx}" for idx in range(n_splits)]

mean_fpr = np.linspace(0, 1, 100)
interp_tprs = []

_, ax = plt.subplots(figsize=(6, 6))
viz = RocCurveDisplay.from_cv_results(
    cv_results,
    X,
    y,
    ax=ax,
    name=names,
    curve_kwargs=curve_kwargs_list,
    plot_chance_level=True,
)

for idx in range(n_splits):
    interp_tpr = np.interp(mean_fpr, viz.fpr[idx], viz.tpr[idx])
    interp_tpr[0] = 0.0
    interp_tprs.append(interp_tpr)

mean_tpr = np.mean(interp_tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(viz.roc_auc)

ax.plot(
    mean_fpr,
    mean_tpr,
    color="b",
    label=r"Mean ROC (AUC = %0.2f $\pm$ %0.2f)" % (mean_auc, std_auc),
    lw=2,
    alpha=0.8,
)

std_tpr = np.std(interp_tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
ax.fill_between(
    mean_fpr,
    tprs_lower,
    tprs_upper,
    color="grey",
    alpha=0.2,
    label=r"$\pm$ 1 std. dev.",
)

ax.set(
    xlabel="False Positive Rate",
    ylabel="True Positive Rate",
    title=f"Mean ROC curve with variability\n(Positive label '{target_names[1]}')",
)
ax.legend(loc="lower right")
plt.show()

Связанные примеры

Многоклассовая рабочая характеристика приемника (ROC)

Многоклассовая рабочая характеристика приемника (ROC)

Кривая ROC с API визуализации

Кривая ROC с API визуализации

Кривая компромисса ошибок обнаружения (DET)

Кривая компромисса ошибок обнаружения (DET)

Построение многоклассового SGD на наборе данных iris

Построение многоклассового SGD на наборе данных iris