Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Эллипсоиды гауссовской смеси#
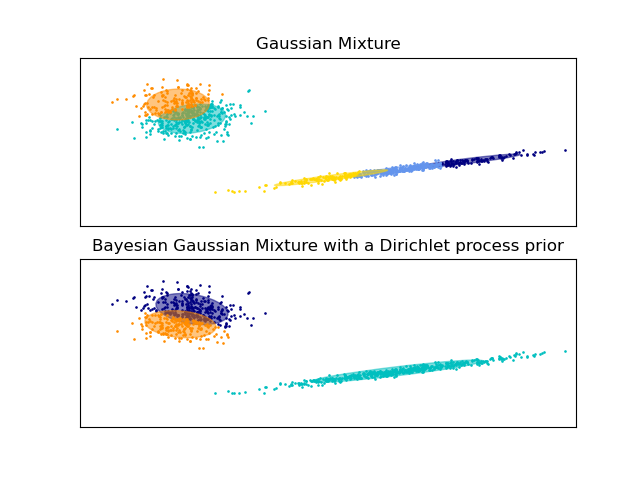
Постройте доверительные эллипсоиды смеси двух гауссовых распределений,
полученных с помощью алгоритма максимизации ожидания (GaussianMixture класс) и Вариационный вывод (BayesianGaussianMixture классовые модели с априорным распределением Дирихле).
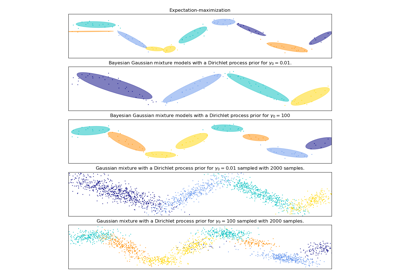
Обе модели имеют доступ к пяти компонентам для подгонки данных. Обратите внимание, что модель Expectation Maximisation обязательно использует все пять компонентов, в то время как модель Variational Inference фактически использует только столько, сколько необходимо для хорошей подгонки. Здесь мы видим, что модель Expectation Maximisation произвольно разделяет некоторые компоненты, потому что она пытается подогнать слишком много компонентов, в то время как модель Dirichlet Process автоматически адаптирует количество состояний.
Этот пример не показывает этого, так как мы находимся в пространстве низкой размерности, но ещё одно преимущество модели процесса Дирихле заключается в том, что она может эффективно обучать полные ковариационные матрицы даже когда примеров на кластер меньше, чем размерностей в данных, благодаря регуляризационным свойствам алгоритма вывода.
/home/circleci/project/sklearn/mixture/_base.py:293: ConvergenceWarning:
Best performing initialization did not converge. Try different init parameters, or increase max_iter, tol, or check for degenerate data.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import itertools
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
from sklearn import mixture
color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])
def plot_results(X, Y_, means, covariances, index, title):
splot = plt.subplot(2, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y_ == i):
continue
plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180.0 * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-9.0, 5.0)
plt.ylim(-3.0, 6.0)
plt.xticks(())
plt.yticks(())
plt.title(title)
# Number of samples per component
n_samples = 500
# Generate random sample, two components
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
X = np.r_[
np.dot(np.random.randn(n_samples, 2), C),
0.7 * np.random.randn(n_samples, 2) + np.array([-6, 3]),
]
# Fit a Gaussian mixture with EM using five components
gmm = mixture.GaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Gaussian Mixture")
# Fit a Dirichlet process Gaussian mixture using five components
dpgmm = mixture.BayesianGaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(
X,
dpgmm.predict(X),
dpgmm.means_,
dpgmm.covariances_,
1,
"Bayesian Gaussian Mixture with a Dirichlet process prior",
)
plt.show()
Общее время выполнения скрипта: (0 минут 0.216 секунд)
Связанные примеры
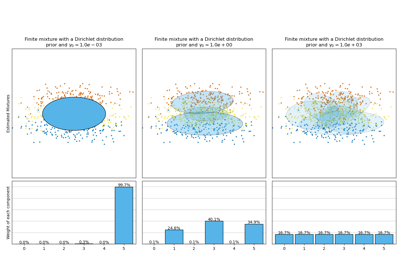
Анализ вариации байесовской гауссовой смеси с априорным типом концентрации