Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Гауссова смесь моделей синусоидальной кривой#

Этот пример демонстрирует поведение моделей гауссовских смесей, обученных на данных, которые не были получены из смеси гауссовских случайных величин. Набор данных состоит из 100 точек, свободно расположенных вдоль зашумленной синусоидальной кривой. Следовательно, нет истинного значения для количества гауссовских компонент.

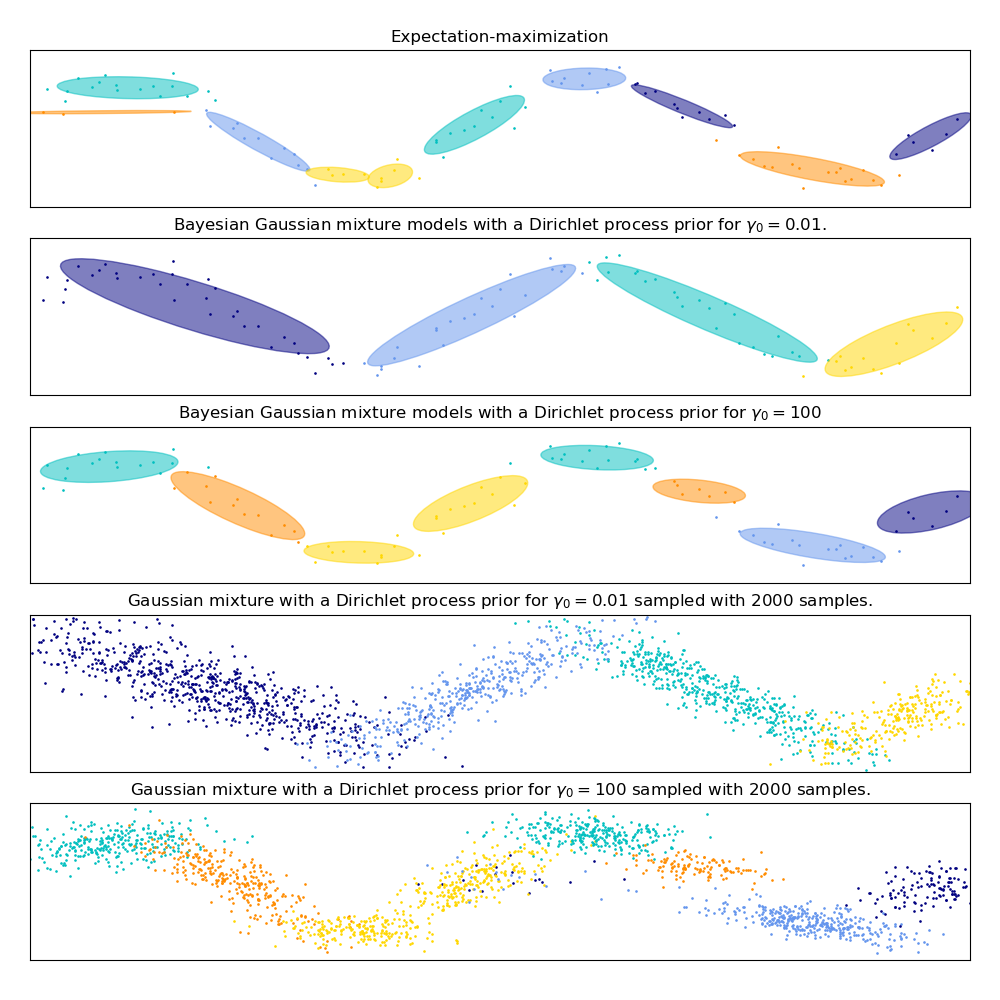
Первая модель - классическая гауссовская смесь с 10 компонентами, обученная алгоритмом максимизации ожидания.

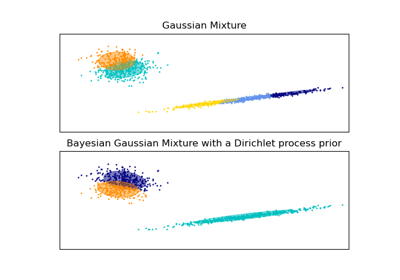
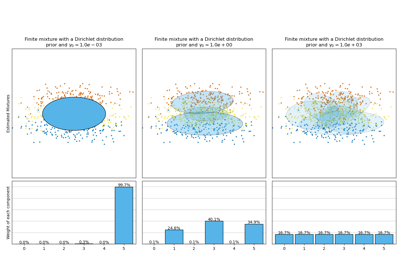
Вторая модель — это байесовская гауссовская смесь с априорным распределением Дирихле, обученная с использованием вариационного вывода. Низкое значение априорной концентрации заставляет модель предпочитать меньшее количество активных компонентов. Эта модель «решает» сосредоточить свою мощность моделирования на общей структуре набора данных: группы точек с чередующимися направлениями, моделируемые недиагональными ковариационными матрицами. Эти чередующиеся направления примерно отражают чередующуюся природу исходного синусоидального сигнала.

Третья модель также является байесовской гауссовской смесью с априорным распределением Дирихле, но на этот раз значение априорной концентрации выше, что дает модели больше свободы для моделирования детальной структуры данных. Результатом является смесь с большим количеством активных компонентов, которая похожа на первую модель, где мы произвольно решили зафиксировать количество компонентов на 10.

Какая модель лучше — вопрос субъективного суждения: хотим ли мы отдавать предпочтение моделям, которые захватывают только общую картину, чтобы обобщить и объяснить большую часть структуры данных, игнорируя детали, или мы предпочитаем модели, которые тесно следуют областям высокой плотности сигнала?

Последние две панели показывают, как мы можем сэмплировать из последних двух моделей. Полученные распределения сэмплов не выглядят точно как исходное распределение данных. Разница в основном возникает из-за ошибки аппроксимации, которую мы допустили, используя модель, предполагающую, что данные были сгенерированы конечным числом гауссовых компонент вместо непрерывной зашумлённой синусоидальной кривой.

$Expectation-maximization, Bayesian Gaussian mixture models with a Dirichlet process prior for $\gamma_0=0.01$., Gaussian mixture with a Dirichlet process prior for $\gamma_0=0.01$ sampled with $2000$ samples., Bayesian Gaussian mixture models with a Dirichlet process prior for $\gamma_0=100$, Gaussian mixture with a Dirichlet process prior for $\gamma_0=100$ sampled with $2000$ samples.$

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import itertools

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg

from sklearn import mixture

color_iter = itertools.cycle(["navy", "c", "cornflowerblue", "gold", "darkorange"])


def plot_results(X, Y, means, covariances, index, title):
    splot = plt.subplot(5, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)

        # Plot an ellipse to show the Gaussian component
        angle = np.arctan(u[1] / u[0])
        angle = 180.0 * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-6.0, 4.0 * np.pi - 6.0)
    plt.ylim(-5.0, 5.0)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


def plot_samples(X, Y, n_components, index, title):
    plt.subplot(5, 1, 4 + index)
    for i, color in zip(range(n_components), color_iter):
        # as the DP will not use every component it has access to
        # unless it needs it, we shouldn't plot the redundant
        # components.
        if not np.any(Y == i):
            continue
        plt.scatter(X[Y == i, 0], X[Y == i, 1], 0.8, color=color)

    plt.xlim(-6.0, 4.0 * np.pi - 6.0)
    plt.ylim(-5.0, 5.0)
    plt.title(title)
    plt.xticks(())
    plt.yticks(())


# Parameters
n_samples = 100

# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4.0 * np.pi / n_samples

for i in range(X.shape[0]):
    x = i * step - 6.0
    X[i, 0] = x + np.random.normal(0, 0.1)
    X[i, 1] = 3.0 * (np.sin(x) + np.random.normal(0, 0.2))

plt.figure(figsize=(10, 10))
plt.subplots_adjust(
    bottom=0.04, top=0.95, hspace=0.2, wspace=0.05, left=0.03, right=0.97
)

# Fit a Gaussian mixture with EM using ten components
gmm = mixture.GaussianMixture(
    n_components=10, covariance_type="full", max_iter=100
).fit(X)
plot_results(
    X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Expectation-maximization"
)

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10,
    covariance_type="full",
    weight_concentration_prior=1e-2,
    weight_concentration_prior_type="dirichlet_process",
    mean_precision_prior=1e-2,
    covariance_prior=1e0 * np.eye(2),
    init_params="random",
    max_iter=100,
    random_state=2,
).fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    1,
    "Bayesian Gaussian mixture models with a Dirichlet process prior "
    r"for $\gamma_0=0.01$.",
)

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
    X_s,
    y_s,
    dpgmm.n_components,
    0,
    "Gaussian mixture with a Dirichlet process prior "
    r"for $\gamma_0=0.01$ sampled with $2000$ samples.",
)

dpgmm = mixture.BayesianGaussianMixture(
    n_components=10,
    covariance_type="full",
    weight_concentration_prior=1e2,
    weight_concentration_prior_type="dirichlet_process",
    mean_precision_prior=1e-2,
    covariance_prior=1e0 * np.eye(2),
    init_params="kmeans",
    max_iter=100,
    random_state=2,
).fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    2,
    "Bayesian Gaussian mixture models with a Dirichlet process prior "
    r"for $\gamma_0=100$",
)

X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(
    X_s,
    y_s,
    dpgmm.n_components,
    1,
    "Gaussian mixture with a Dirichlet process prior "
    r"for $\gamma_0=100$ sampled with $2000$ samples.",
)

plt.show()