Выбор модели гауссовской смеси

Этот пример показывает, что выбор модели может быть выполнен с Гауссовыми смесями (GMM) с использованием информационно-теоретические критерии. Выбор модели касается как типа ковариации, так и количества компонентов в модели.

В этом случае как информационный критерий Акаике (AIC), так и байесовский информационный критерий (BIC) дают правильный результат, но мы демонстрируем только последний, так как BIC лучше подходит для идентификации истинной модели среди набора кандидатов. В отличие от байесовских процедур, такие выводы не требуют априорных предположений.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Генерация данных

Мы генерируем две компоненты (каждая содержит n_samples) путем случайного выборки из стандартного нормального распределения, возвращаемого numpy.random.randn. Один компонент остаётся сферическим, но смещённым и перемасштабированным. Другой деформируется, чтобы иметь более общую ковариационную матрицу.

import numpy as np

n_samples = 500
np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
component_1 = np.dot(np.random.randn(n_samples, 2), C)  # general
component_2 = 0.7 * np.random.randn(n_samples, 2) + np.array([-4, 1])  # spherical

X = np.concatenate([component_1, component_2])

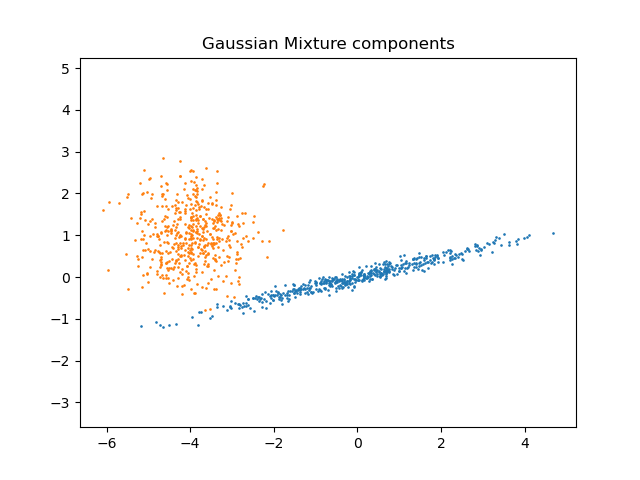
Мы можем визуализировать различные компоненты:

import matplotlib.pyplot as plt

plt.scatter(component_1[:, 0], component_1[:, 1], s=0.8)
plt.scatter(component_2[:, 0], component_2[:, 1], s=0.8)
plt.title("Gaussian Mixture components")
plt.axis("equal")
plt.show()

Обучение и выбор модели

Мы варьируем количество компонентов от 1 до 6 и тип используемых параметров ковариации:

• "full": каждый компонент имеет свою общую ковариационную матрицу.

• "tied": все компоненты используют одну и ту же общую ковариационную матрицу.

• "diag": каждый компонент имеет свою собственную диагональную ковариационную матрицу.

• "spherical": каждый компонент имеет свою собственную единичную дисперсию.

Мы оцениваем различные модели и сохраняем лучшую модель (с наименьшим BIC). Это делается с помощью GridSearchCV и пользовательская функция оценки, которая возвращает отрицательный балл BIC, как GridSearchCV разработан для максимизировать оценка (максимизация отрицательного BIC эквивалентна минимизации BIC).

Лучший набор параметров и оценщик хранятся в best_parameters_ и best_estimator_, соответственно.

from sklearn.mixture import GaussianMixture
from sklearn.model_selection import GridSearchCV


def gmm_bic_score(estimator, X):
    """Callable to pass to GridSearchCV that will use the BIC score."""
    # Make it negative since GridSearchCV expects a score to maximize
    return -estimator.bic(X)


param_grid = {
    "n_components": range(1, 7),
    "covariance_type": ["spherical", "tied", "diag", "full"],
}
grid_search = GridSearchCV(
    GaussianMixture(), param_grid=param_grid, scoring=gmm_bic_score
)
grid_search.fit(X)

GridSearchCV(estimator=GaussianMixture(),
             param_grid={'covariance_type': ['spherical', 'tied', 'diag',
                                             'full'],
                         'n_components': range(1, 7)},
             scoring=)

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Построить график оценок BIC

Чтобы упростить построение графика, мы можем создать pandas.DataFrame из результатов кросс-валидации, выполненной при поиске по сетке. Мы обратно инвертируем знак оценки BIC, чтобы показать эффект её минимизации.

import pandas as pd

df = pd.DataFrame(grid_search.cv_results_)[
    ["param_n_components", "param_covariance_type", "mean_test_score"]
]
df["mean_test_score"] = -df["mean_test_score"]
df = df.rename(
    columns={
        "param_n_components": "Number of components",
        "param_covariance_type": "Type of covariance",
        "mean_test_score": "BIC score",
    }
)
df.sort_values(by="BIC score").head()

	Количество компонент	Тип ковариации	оценка BIC
19	2	полный	1046.829429
20	3	полный	1084.038689
21	4	полный	1114.517272
22	5	полный	1148.512281
23	6	полный	1179.977890

import seaborn as sns

sns.catplot(
    data=df,
    kind="bar",
    x="Number of components",
    y="BIC score",
    hue="Type of covariance",
)
plt.show()

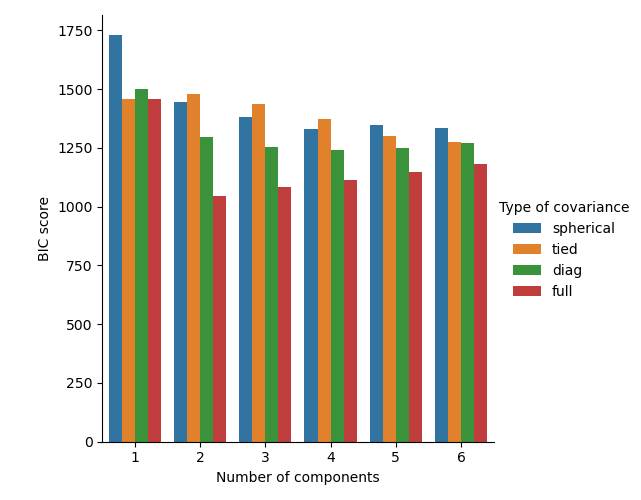
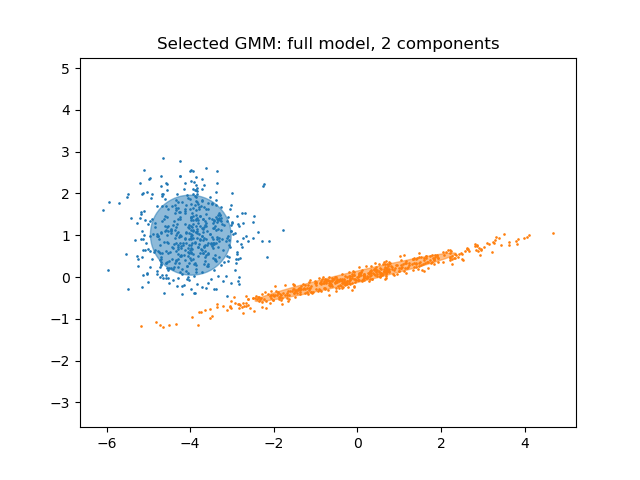
В данном случае модель с 2 компонентами и полной ковариацией (что соответствует истинной генеративной модели) имеет наименьший показатель BIC и поэтому выбрана при поиске по сетке.

Построить график лучшей модели

Мы строим эллипс, чтобы показать каждую гауссову компоненту выбранной модели. Для этой цели необходимо найти собственные значения ковариационных матриц, как возвращённые covariances_ атрибут. Форма таких матриц зависит от covariance_type:

• "full": (n_components, n_features, n_features)

• "tied": (n_features, n_features)

• "diag": (n_components, n_features)

• "spherical": (n_components,)

from matplotlib.patches import Ellipse
from scipy import linalg

color_iter = sns.color_palette("tab10", 2)[::-1]
Y_ = grid_search.predict(X)

fig, ax = plt.subplots()

for i, (mean, cov, color) in enumerate(
    zip(
        grid_search.best_estimator_.means_,
        grid_search.best_estimator_.covariances_,
        color_iter,
    )
):
    v, w = linalg.eigh(cov)
    if not np.any(Y_ == i):
        continue
    plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)

    angle = np.arctan2(w[0][1], w[0][0])
    angle = 180.0 * angle / np.pi  # convert to degrees
    v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
    ellipse = Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
    ellipse.set_clip_box(fig.bbox)
    ellipse.set_alpha(0.5)
    ax.add_artist(ellipse)

plt.title(
    f"Selected GMM: {grid_search.best_params_['covariance_type']} model, "
    f"{grid_search.best_params_['n_components']} components"
)
plt.axis("equal")
plt.show()

Связанные примеры

Эллипсоиды гауссовской смеси

Эллипсоиды гауссовской смеси

Выбор модели Lasso с помощью информационных критериев

Выбор модели Lasso с помощью информационных критериев

Линейный и квадратичный дискриминантный анализ с эллипсоидом ковариации

Линейный и квадратичный дискриминантный анализ с эллипсоидом ковариации

Гауссова смесь моделей синусоидальной кривой

Гауссова смесь моделей синусоидальной кривой