Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Калибровка вероятностей для классификации на 3 класса#
Этот пример иллюстрирует, как сигмоида калибровка изменяет предсказанные вероятности для задачи классификации с 3 классами. Проиллюстрирован стандартный 2-симплекс, где три угла соответствуют трём классам. Стрелки указывают от векторов вероятностей, предсказанных некалиброванным классификатором, к векторам вероятностей, предсказанным тем же классификатором после сигмоидной калибровки на валидационной выборке. Цвета указывают истинный класс экземпляра (красный: класс 1, зелёный: класс 2, синий: класс 3).
Данные#
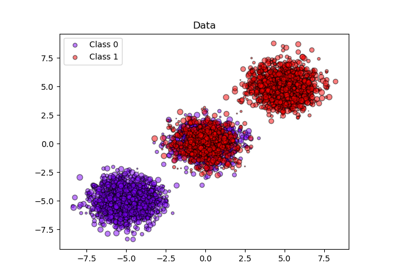
Ниже мы генерируем набор данных для классификации с 2000 образцами, 2 признаками и 3 целевыми классами. Затем мы разделяем данные следующим образом:
обучение: 600 образцов (для обучения классификатора)
валидация: 400 образцов (для калибровки предсказанных вероятностей)
тест: 1000 образцов
Обратите внимание, что мы также создаем X_train_valid и y_train_valid, который включает как обучающую, так и валидационную подвыборки. Используется, когда нужно только обучить классификатор без калибровки предсказанных вероятностей.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from sklearn.datasets import make_blobs
np.random.seed(0)
X, y = make_blobs(
n_samples=2000, n_features=2, centers=3, random_state=42, cluster_std=5.0
)
X_train, y_train = X[:600], y[:600]
X_valid, y_valid = X[600:1000], y[600:1000]
X_train_valid, y_train_valid = X[:1000], y[:1000]
X_test, y_test = X[1000:], y[1000:]
Обучение и калибровка#
Сначала мы обучим RandomForestClassifier
с 25 базовыми оценщиками (деревьями) на объединенных обучающих и валидационных данных (1000 образцов). Это некалиброванный классификатор.
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train_valid, y_train_valid)
Для обучения калиброванного классификатора мы начинаем с того же
RandomForestClassifier но обучить его используя только
подмножество обучающих данных (600 образцов), затем откалибровать, с method='sigmoid',
используя допустимое подмножество данных (400 образцов) в двухэтапном процессе.
from sklearn.calibration import CalibratedClassifierCV
from sklearn.frozen import FrozenEstimator
clf = RandomForestClassifier(n_estimators=25)
clf.fit(X_train, y_train)
cal_clf = CalibratedClassifierCV(FrozenEstimator(clf), method="sigmoid")
cal_clf.fit(X_valid, y_valid)
Сравнить вероятности#
Ниже мы строим 2-симплекс со стрелками, показывающими изменение предсказанных вероятностей тестовых выборок.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
colors = ["r", "g", "b"]
clf_probs = clf.predict_proba(X_test)
cal_clf_probs = cal_clf.predict_proba(X_test)
# Plot arrows
for i in range(clf_probs.shape[0]):
plt.arrow(
clf_probs[i, 0],
clf_probs[i, 1],
cal_clf_probs[i, 0] - clf_probs[i, 0],
cal_clf_probs[i, 1] - clf_probs[i, 1],
color=colors[y_test[i]],
head_width=1e-2,
)
# Plot perfect predictions, at each vertex
plt.plot([1.0], [0.0], "ro", ms=20, label="Class 1")
plt.plot([0.0], [1.0], "go", ms=20, label="Class 2")
plt.plot([0.0], [0.0], "bo", ms=20, label="Class 3")
# Plot boundaries of unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
# Annotate points 6 points around the simplex, and mid point inside simplex
plt.annotate(
r"($\frac{1}{3}$, $\frac{1}{3}$, $\frac{1}{3}$)",
xy=(1.0 / 3, 1.0 / 3),
xytext=(1.0 / 3, 0.23),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.plot([1.0 / 3], [1.0 / 3], "ko", ms=5)
plt.annotate(
r"($\frac{1}{2}$, $0$, $\frac{1}{2}$)",
xy=(0.5, 0.0),
xytext=(0.5, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $\frac{1}{2}$, $\frac{1}{2}$)",
xy=(0.0, 0.5),
xytext=(0.1, 0.5),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($\frac{1}{2}$, $\frac{1}{2}$, $0$)",
xy=(0.5, 0.5),
xytext=(0.6, 0.6),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $0$, $1$)",
xy=(0, 0),
xytext=(0.1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($1$, $0$, $0$)",
xy=(1, 0),
xytext=(1, 0.1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
plt.annotate(
r"($0$, $1$, $0$)",
xy=(0, 1),
xytext=(0.1, 1),
xycoords="data",
arrowprops=dict(facecolor="black", shrink=0.05),
horizontalalignment="center",
verticalalignment="center",
)
# Add grid
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Change of predicted probabilities on test samples after sigmoid calibration")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
_ = plt.legend(loc="best")
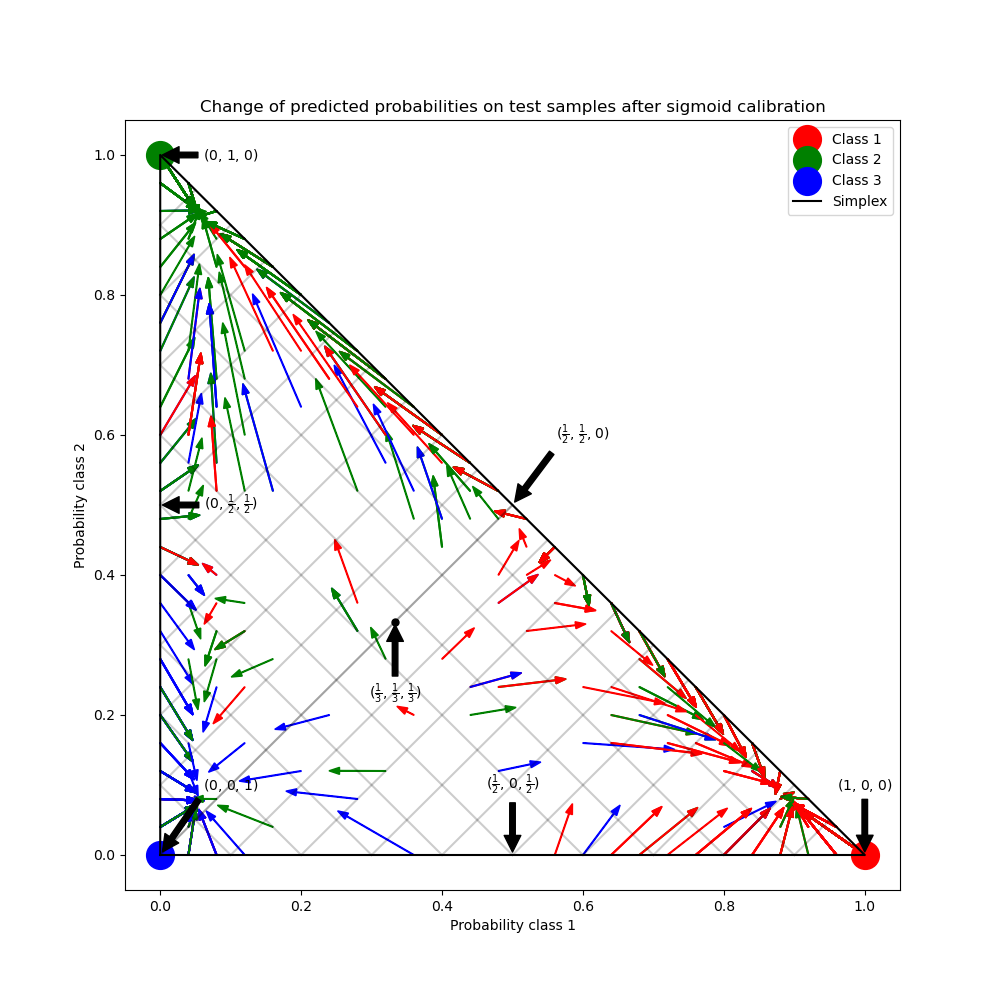
На рисунке выше каждая вершина симплекса представляет идеально предсказанный класс (например, 1, 0, 0). Средняя точка внутри симплекса представляет предсказание трех классов с равной вероятностью (т.е., 1/3, 1/3, 1/3). Каждая стрелка начинается от некалиброванных вероятностей и заканчивается на калиброванной вероятности. Цвет стрелки представляет истинный класс этого тестового образца.
Некорректированный классификатор излишне уверен в своих предсказаниях и несёт большие логарифмические потери. Калиброванный классификатор имеет более низкую логарифмические потери из-за двух факторов. Во-первых, обратите внимание на рисунок выше, что стрелки обычно указывают от краёв симплекса, где вероятность одного класса равна 0. Во-вторых, большая часть стрелок указывает на истинный класс, например, зелёные стрелки (образцы, где истинный класс — 'зелёный') обычно указывают на зелёную вершину. Это приводит к меньшему количеству излишне уверенных предсказанных вероятностей, равных 0, и одновременно увеличению предсказанных вероятностей правильного класса. Таким образом, калиброванный классификатор даёт более точные предсказанные вероятности, которые приводят к меньшей логарифмические потери
Мы можем показать это объективно, сравнив логарифмические потери некалиброванных и калиброванных классификаторов на предсказаниях 1000
тестовых образцов. Обратите внимание, что альтернативой могло бы быть увеличение количества
базовых оценщиков (деревьев) в
RandomForestClassifier что привело бы к аналогичному снижению логарифмические потери.
Log-loss of:
- uncalibrated classifier: 1.327
- calibrated classifier: 0.549
Мы также можем оценить калибровку с помощью оценки Брайера для вероятностных предсказаний (ниже — лучше, возможный диапазон [0, 2]):
from sklearn.metrics import brier_score_loss
loss = brier_score_loss(y_test, clf_probs)
cal_loss = brier_score_loss(y_test, cal_clf_probs)
print("Brier score of")
print(f" - uncalibrated classifier: {loss:.3f}")
print(f" - calibrated classifier: {cal_loss:.3f}")
Brier score of
- uncalibrated classifier: 0.308
- calibrated classifier: 0.310
Согласно оценке Брайера, калиброванный классификатор не лучше исходной модели.
Наконец, мы генерируем сетку возможных некалиброванных вероятностей над 2-симплексом, вычисляем соответствующие калиброванные вероятности и строим стрелки для каждой. Стрелки окрашены в соответствии с наибольшей некалиброванной вероятностью. Это иллюстрирует изученную карту калибровки:
plt.figure(figsize=(10, 10))
# Generate grid of probability values
p1d = np.linspace(0, 1, 20)
p0, p1 = np.meshgrid(p1d, p1d)
p2 = 1 - p0 - p1
p = np.c_[p0.ravel(), p1.ravel(), p2.ravel()]
p = p[p[:, 2] >= 0]
# Use the three class-wise calibrators to compute calibrated probabilities
calibrated_classifier = cal_clf.calibrated_classifiers_[0]
prediction = np.vstack(
[
calibrator.predict(this_p)
for calibrator, this_p in zip(calibrated_classifier.calibrators, p.T)
]
).T
# Re-normalize the calibrated predictions to make sure they stay inside the
# simplex. This same renormalization step is performed internally by the
# predict method of CalibratedClassifierCV on multiclass problems.
prediction /= prediction.sum(axis=1)[:, None]
# Plot changes in predicted probabilities induced by the calibrators
for i in range(prediction.shape[0]):
plt.arrow(
p[i, 0],
p[i, 1],
prediction[i, 0] - p[i, 0],
prediction[i, 1] - p[i, 1],
head_width=1e-2,
color=colors[np.argmax(p[i])],
)
# Plot the boundaries of the unit simplex
plt.plot([0.0, 1.0, 0.0, 0.0], [0.0, 0.0, 1.0, 0.0], "k", label="Simplex")
plt.grid(False)
for x in [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
plt.plot([0, x], [x, 0], "k", alpha=0.2)
plt.plot([0, 0 + (1 - x) / 2], [x, x + (1 - x) / 2], "k", alpha=0.2)
plt.plot([x, x + (1 - x) / 2], [0, 0 + (1 - x) / 2], "k", alpha=0.2)
plt.title("Learned sigmoid calibration map")
plt.xlabel("Probability class 1")
plt.ylabel("Probability class 2")
plt.xlim(-0.05, 1.05)
plt.ylim(-0.05, 1.05)
plt.show()
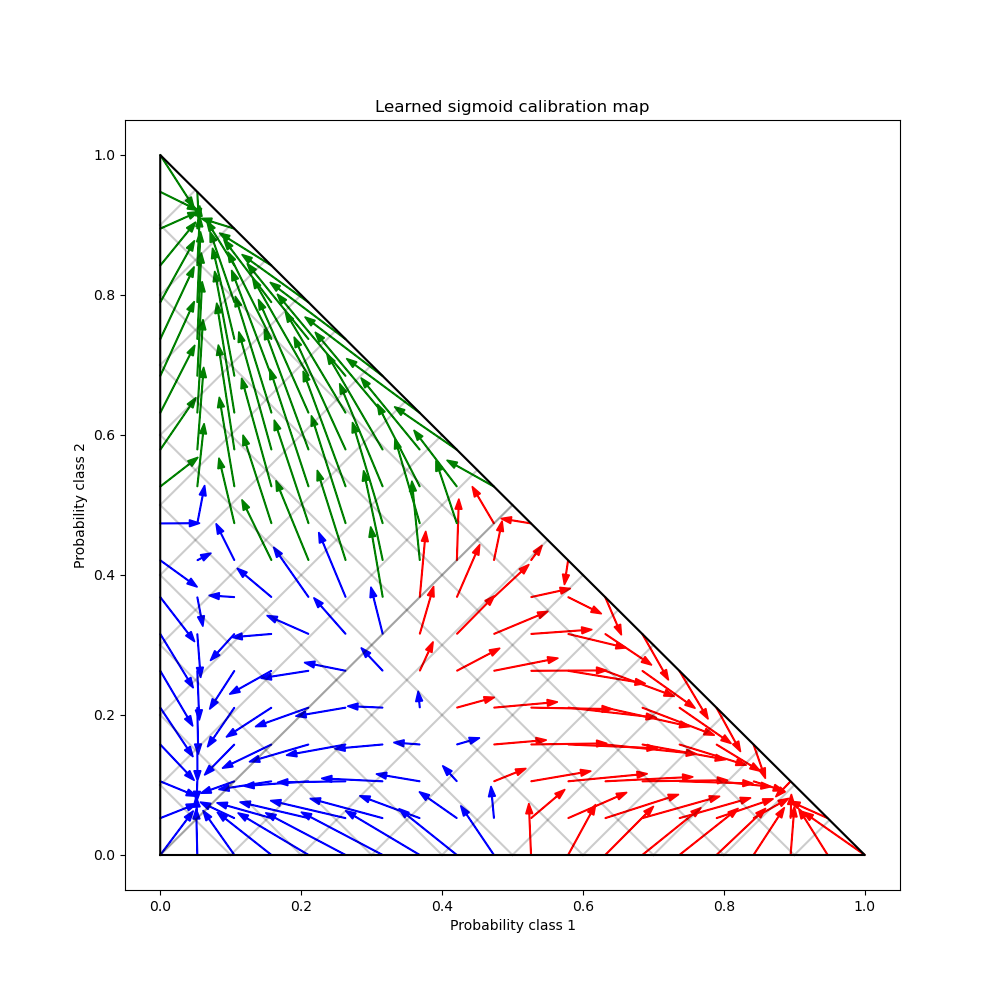
Можно заметить, что в среднем калибратор отталкивает высокоуверенные предсказания от границ симплекса, одновременно приближая неуверенные предсказания к одному из трех мод, по одной для каждого класса. Также можно заметить, что отображение несимметрично. Более того, некоторые стрелки, кажется, пересекают границы назначения классов, что не обязательно ожидается от карты калибровки, так как это означает, что некоторые предсказанные классы изменятся после калибрации.
В целом, стратегия многоклассовой калибровки «Один против остальных», реализованная в
CalibratedClassifierCV не следует слепо доверять.
Общее время выполнения скрипта: (0 минут 1.240 секунд)
Связанные примеры