Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Сравнение калибровки классификаторов#
Хорошо калиброванные классификаторы — это вероятностные классификаторы, для которых выход predict_proba может быть напрямую интерпретирован как уровень доверия. Например, хорошо калиброванный (бинарный) классификатор должен классифицировать образцы таким образом, что для образцов, которым он присвоил predict_proba значение близко к 0.8, примерно 80% фактически принадлежат положительному классу.
В этом примере мы сравним калибровку четырех различных моделей: Логистическая регрессия, Наивный байесовский классификатор с гауссовским распределением, Random Forest Classifier и Линейный SVM.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
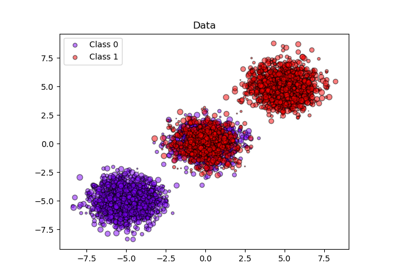
Набор данных#
Мы будем использовать синтетический набор данных для бинарной классификации с 100 000 образцов и 20 признаками. Из 20 признаков только 2 являются информативными, 2 - избыточными (случайные комбинации информативных признаков), а оставшиеся 16 - неинформативными (случайные числа).
Из 100 000 образцов 100 будут использованы для обучения модели, а оставшиеся для тестирования. Обратите внимание, что такое разделение довольно необычно: цель — получить стабильные оценки калибровочных кривых для моделей, которые потенциально склонны к переобучению. На практике следует использовать перекрестную проверку с более сбалансированными разбиениями, но это усложнило бы код данного примера.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=100_000, n_features=20, n_informative=2, n_redundant=2, random_state=42
)
train_samples = 100 # Samples used for training the models
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
shuffle=False,
test_size=100_000 - train_samples,
)
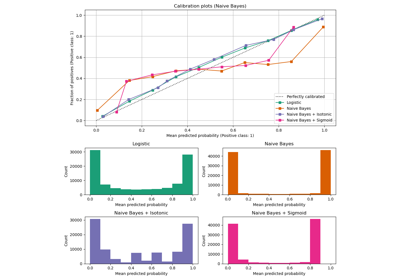
Кривые калибровки#
Ниже мы обучаем каждую из четырёх моделей на небольшом обучающем наборе данных, затем строим калибровочные кривые (также известные как диаграммы надёжности), используя прогнозируемые вероятности тестового набора данных. Калибровочные кривые создаются путём разбиения прогнозируемых вероятностей на бины, затем построения средней прогнозируемой вероятности в каждом бине против наблюдаемой частоты ('доля положительных'). Под калибровочной кривой мы строим гистограмму, показывающую распределение прогнозируемых вероятностей или, более конкретно, количество образцов в каждом бине прогнозируемой вероятности.
import numpy as np
from sklearn.svm import LinearSVC
class NaivelyCalibratedLinearSVC(LinearSVC):
"""LinearSVC with `predict_proba` method that naively scales
`decision_function` output."""
def fit(self, X, y):
super().fit(X, y)
df = self.decision_function(X)
self.df_min_ = df.min()
self.df_max_ = df.max()
def predict_proba(self, X):
"""Min-max scale output of `decision_function` to [0,1]."""
df = self.decision_function(X)
calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
proba_pos_class = np.clip(calibrated_df, 0, 1)
proba_neg_class = 1 - proba_pos_class
proba = np.c_[proba_neg_class, proba_pos_class]
return proba
from sklearn.calibration import CalibrationDisplay
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegressionCV
from sklearn.naive_bayes import GaussianNB
# Define the classifiers to be compared in the study.
#
# Note that we use a variant of the logistic regression model that can
# automatically tune its regularization parameter.
#
# For a fair comparison, we should run a hyper-parameter search for all the
# classifiers but we don't do it here for the sake of keeping the example code
# concise and fast to execute.
lr = LogisticRegressionCV(
Cs=np.logspace(-6, 6, 101),
cv=10,
l1_ratios=(0,),
scoring="neg_log_loss",
max_iter=1_000,
use_legacy_attributes=False,
)
gnb = GaussianNB()
svc = NaivelyCalibratedLinearSVC(C=1.0)
rfc = RandomForestClassifier(random_state=42)
clf_list = [
(lr, "Logistic Regression"),
(gnb, "Naive Bayes"),
(svc, "SVC"),
(rfc, "Random forest"),
]
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
markers = ["^", "v", "s", "o"]
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
marker=markers[i],
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
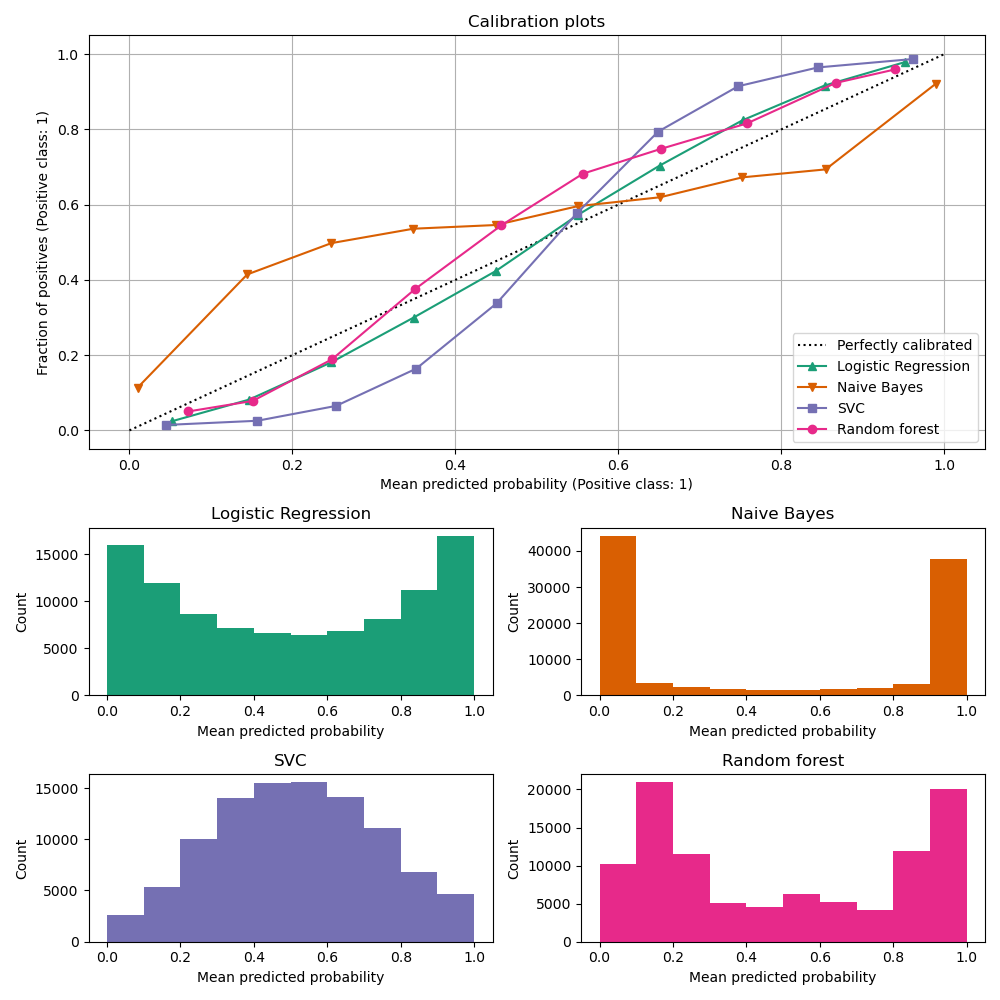
Анализ результатов#
LogisticRegressionCV возвращает достаточно хорошо
калиброванные предсказания, несмотря на небольшой размер обучающей выборки: его кривая надежности
наиболее близка к диагонали среди четырех моделей.
Логистическая регрессия обучается минимизацией лог-потерь, которые являются строго правильным правилом оценки: в пределе бесконечных обучающих данных строго правильные правила оценки минимизируются моделью, предсказывающей истинные условные вероятности. Эта (гипотетическая) модель, следовательно, была бы идеально калибрована. Однако использование правильного правила оценки в качестве цели обучения само по себе недостаточно для гарантии хорошо калиброванной модели: даже с очень большим обучающим набором логистическая регрессия всё ещё может быть плохо калибрована, если она была слишком сильно регуляризована или если выбор и предобработка входных признаков сделали эту модель неверно специфицированной (например, если истинная граница решения набора данных является сильно нелинейной функцией входных признаков).
В этом примере обучающая выборка была намеренно оставлена очень маленькой. В такой настройке оптимизация логарифмической потери всё ещё может приводить к плохо калиброванным моделям из-за переобучения. Чтобы смягчить это,
LogisticRegressionCV класс был настроен для настройки C параметр регуляризации также минимизирует лог-потери через внутреннюю
кросс-валидацию, чтобы найти наилучший компромисс для этой модели в условиях
малого обучающего набора.
Из-за конечного размера обучающей выборки и отсутствия гарантии хорошей спецификации мы наблюдаем, что калибровочная кривая модели логистической регрессии близка, но не идеально лежит на диагонали. Форму калибровочной кривой этой модели можно интерпретировать как слегка недостаточно уверенную: предсказанные вероятности немного слишком близки к 0.5 по сравнению с истинной долей положительных выборок.
Другие методы выводят менее хорошо калиброванные вероятности:
GaussianNBсклонен подталкивать вероятности к 0 или 1 (см. гистограмму) на этом конкретном наборе данных (чрезмерная уверенность). Это в основном потому, что уравнение наивного Байеса дает правильную оценку вероятностей только тогда, когда предположение, что признаки условно независимы, выполняется [2]. Однако признаки могут быть коррелированы, что и происходит с этим набором данных, который содержит 2 признака, сгенерированных как случайные линейные комбинации информативных признаков. Эти коррелированные признаки фактически 'учитываются дважды', что приводит к смещению предсказанных вероятностей к 0 и 1 [3]. Однако обратите внимание, что изменение сида, используемого для генерации набора данных, может привести к сильно различающимся результатам для наивного байесовского оценщика.LinearSVCне является естественным вероятностным классификатором. Чтобы интерпретировать его предсказание как таковое, мы наивно масштабировали выход decision_function в [0, 1] путем применения min-max масштабирования вNaivelyCalibratedLinearSVCкласс-обертка, определенный выше. Этот оценщик показывает типичную сигмоидальную калибровочную кривую на этих данных: предсказания больше 0,5 соответствуют образцам с еще большей эффективной долей положительного класса (выше диагонали), в то время как предсказания ниже 0,5 соответствуют еще меньшим долям положительного класса (ниже диагонали). Эти недостаточно уверенные предсказания типичны для методов максимального запаса [1].RandomForestClassifierгистограмма предсказаний показывает пики примерно при вероятностях 0.2 и 0.9, в то время как вероятности, близкие к 0 или 1, встречаются очень редко. Объяснение этому дано [1]: «Методы, такие как бэггинг и случайные леса, которые усредняют предсказания из базового набора моделей, могут испытывать трудности с предсказаниями около 0 и 1, потому что дисперсия в базовых моделях будет смещать предсказания, которые должны быть около нуля или единицы, от этих значений. Поскольку предсказания ограничены интервалом [0, 1], ошибки, вызванные дисперсией, имеют тенденцию быть односторонними около нуля и единицы. Например, если модель должна предсказать p = 0 для случая, единственный способ, которым бэггинг может достичь этого, — если все деревья в бэггинге предсказывают ноль. Если мы добавим шум к деревьям, которые усредняет бэггинг, этот шум заставит некоторые деревья предсказывать значения больше 0 для этого случая, таким образом смещая среднее предсказание ансамбля бэггинга от 0. Мы наблюдаем этот эффект наиболее сильно в случайных лесах, потому что базовые деревья, обученные в случайных лесах, имеют относительно высокую дисперсию из-за подвыборки признаков.» Этот эффект может сделать случайные леса недостаточно уверенными. Несмотря на это возможное смещение, обратите внимание, что сами деревья обучаются путем минимизации либо критерия Джини, либо энтропии, оба из которых приводят к разбиениям, минимизирующим правильные оценочные правила: соответственно, оценку Брайера или логарифмическую потерю. См. руководство пользователя для получения дополнительных подробностей. Это может объяснить, почему эта модель показывает достаточно хорошую калибровочную кривую на этом конкретном примере набора данных. Действительно, модель Random Forest не является значительно более недоуверенной, чем модель Logistic Regression.
Не стесняйтесь повторно запускать этот пример с разными случайными начальными значениями и другими параметрами генерации набора данных, чтобы увидеть, насколько разными могут быть графики калибровки. Как правило, логистическая регрессия и случайный лес стремятся быть наиболее хорошо калиброванными классификаторами, в то время как SVC часто демонстрирует типичную недостоверную некорректную калибровку. Наивный байесовский классификатор также часто плохо калиброван, но общая форма его кривой калибровки может сильно варьироваться в зависимости от набора данных.
Наконец, обратите внимание, что для некоторых начальных значений набора данных все модели плохо откалиброваны, даже при настройке параметра регуляризации, как указано выше. Это неизбежно происходит, когда размер обучающей выборки слишком мал или когда модель серьёзно неправильно специфицирована.
Ссылки#
Общее время выполнения скрипта: (0 минут 3.184 секунды)
Связанные примеры
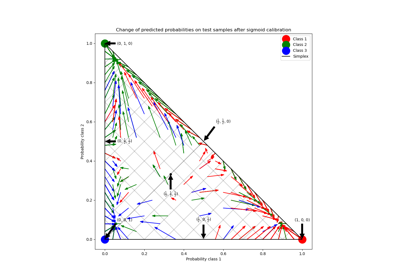
Калибровка вероятностей для классификации на 3 класса