Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Кривые калибровки вероятности#
При выполнении классификации часто хочется предсказать не только метку класса, но и связанную с ней вероятность. Эта вероятность дает некоторую уверенность в прогнозе. Этот пример демонстрирует, как визуализировать, насколько хорошо откалиброваны предсказанные вероятности, используя кривые калибровки, также известные как диаграммы надежности. Также будет продемонстрирована калибровка некалиброванного классификатора.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Набор данных#
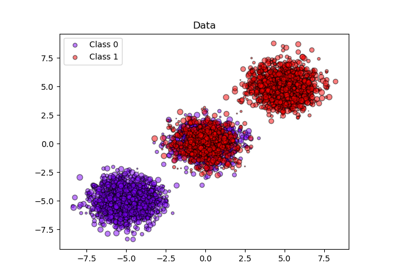
Мы будем использовать синтетический набор данных для бинарной классификации с 100 000 образцов и 20 признаками. Из 20 признаков только 2 являются информативными, 10 — избыточными (случайные комбинации информативных признаков), а оставшиеся 8 — неинформативными (случайные числа). Из 100 000 образцов 1 000 будет использовано для обучения модели, а остальные — для тестирования.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
X, y = make_classification(
n_samples=100_000, n_features=20, n_informative=2, n_redundant=10, random_state=42
)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.99, random_state=42
)
Кривые калибровки#
Наивный байесовский классификатор с гауссовским распределением#
Сначала мы сравним:
LogisticRegression(используется как базовый уровень, поскольку очень часто правильно регуляризованная логистическая регрессия хорошо калибрована по умолчанию благодаря использованию логарифмической потери)Некалиброванный
GaussianNBGaussianNBс изотонической и сигмоидальной калибровкой (см. Руководство пользователя)
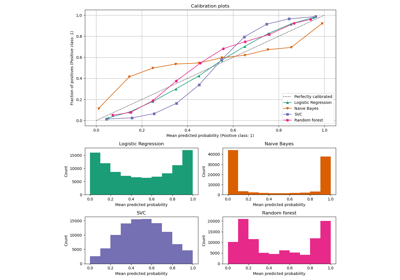
Кривые калибровки для всех 4 условий построены ниже, со средним прогнозируемым вероятностью для каждого бина по оси x и долей положительных классов в каждом бине по оси y.
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
lr = LogisticRegression(C=1.0)
gnb = GaussianNB()
gnb_isotonic = CalibratedClassifierCV(gnb, cv=2, method="isotonic")
gnb_sigmoid = CalibratedClassifierCV(gnb, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(gnb, "Naive Bayes"),
(gnb_isotonic, "Naive Bayes + Isotonic"),
(gnb_sigmoid, "Naive Bayes + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
colors = plt.get_cmap("Dark2")
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (Naive Bayes)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
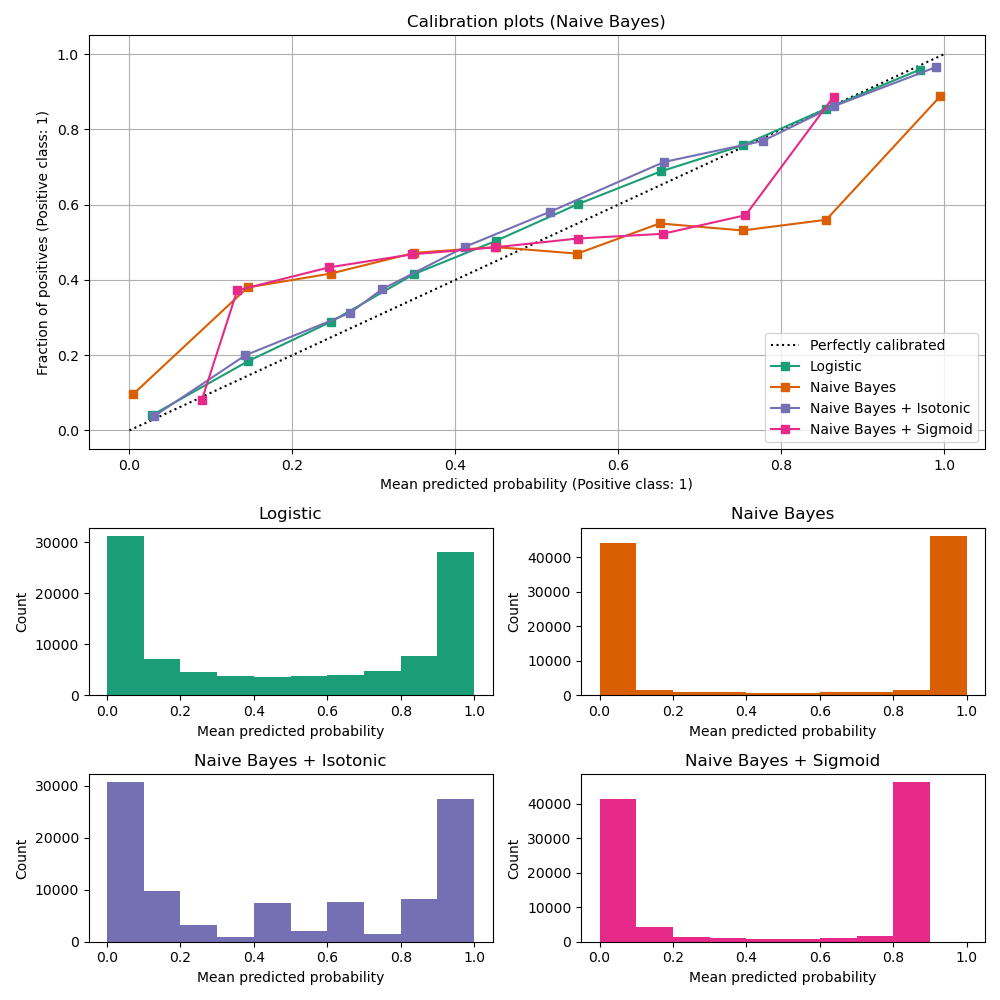
Некалиброванный GaussianNB плохо откалиброван из-за избыточных признаков, которые нарушают предположение о независимости признаков и приводят к излишне уверенному классификатору, что указывается типичной транспонированной сигмоидной кривой. Калибровка вероятностей
GaussianNB с Изотоническая регрессия может исправить эту проблему, как видно из почти диагональной калибровочной кривой.
Сигмоидная регрессия также немного улучшает калибровку, хотя и не так сильно, как непараметрическая изотоническая регрессия. Это можно объяснить тем, что у нас достаточно данных для калибровки, так что можно использовать большую гибкость непараметрической модели.
Ниже мы проведем количественный анализ с учетом нескольких метрик классификации: Потеря по шкале Брайера, Логарифмическая потеря, точность, полнота, F1-мера и ROC AUC.
from collections import defaultdict
import pandas as pd
from sklearn.metrics import (
brier_score_loss,
f1_score,
log_loss,
precision_score,
recall_score,
roc_auc_score,
)
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
Обратите внимание, что хотя калибровка улучшает Потеря по шкале Брайера (метрика, состоящая из калибровочного члена и уточняющего члена) и Логарифмическая потеря, это не значительно изменяет метрики точности прогнозирования (точность, полноту и F1-оценку). Это происходит потому, что калибровка не должна значительно изменять вероятности прогнозирования в точке порога принятия решения (при x = 0.5 на графике). Однако калибровка должна делать предсказанные вероятности более точными и, следовательно, более полезными для принятия решений о распределении в условиях неопределенности. Кроме того, ROC AUC не должен изменяться вообще, поскольку калибровка является монотонным преобразованием. Действительно, ранговые метрики не затрагиваются калибровкой.
Линейный классификатор методом опорных векторов#
Далее мы сравним:
LogisticRegression(базовая линия)Некалиброванный
LinearSVC. Поскольку SVC по умолчанию не выводит вероятности, мы наивно масштабируем выходные данные decision_function в [0, 1] путем применения min-max масштабирования.LinearSVCс изотонической и сигмоидальной калибровкой (см. Руководство пользователя)
import numpy as np
from sklearn.svm import LinearSVC
class NaivelyCalibratedLinearSVC(LinearSVC):
"""LinearSVC with `predict_proba` method that naively scales
`decision_function` output for binary classification."""
def fit(self, X, y):
super().fit(X, y)
df = self.decision_function(X)
self.df_min_ = df.min()
self.df_max_ = df.max()
def predict_proba(self, X):
"""Min-max scale output of `decision_function` to [0, 1]."""
df = self.decision_function(X)
calibrated_df = (df - self.df_min_) / (self.df_max_ - self.df_min_)
proba_pos_class = np.clip(calibrated_df, 0, 1)
proba_neg_class = 1 - proba_pos_class
proba = np.c_[proba_neg_class, proba_pos_class]
return proba
lr = LogisticRegression(C=1.0)
svc = NaivelyCalibratedLinearSVC(max_iter=10_000)
svc_isotonic = CalibratedClassifierCV(svc, cv=2, method="isotonic")
svc_sigmoid = CalibratedClassifierCV(svc, cv=2, method="sigmoid")
clf_list = [
(lr, "Logistic"),
(svc, "SVC"),
(svc_isotonic, "SVC + Isotonic"),
(svc_sigmoid, "SVC + Sigmoid"),
]
fig = plt.figure(figsize=(10, 10))
gs = GridSpec(4, 2)
ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
display = CalibrationDisplay.from_estimator(
clf,
X_test,
y_test,
n_bins=10,
name=name,
ax=ax_calibration_curve,
color=colors(i),
)
calibration_displays[name] = display
ax_calibration_curve.grid()
ax_calibration_curve.set_title("Calibration plots (SVC)")
# Add histogram
grid_positions = [(2, 0), (2, 1), (3, 0), (3, 1)]
for i, (_, name) in enumerate(clf_list):
row, col = grid_positions[i]
ax = fig.add_subplot(gs[row, col])
ax.hist(
calibration_displays[name].y_prob,
range=(0, 1),
bins=10,
label=name,
color=colors(i),
)
ax.set(title=name, xlabel="Mean predicted probability", ylabel="Count")
plt.tight_layout()
plt.show()
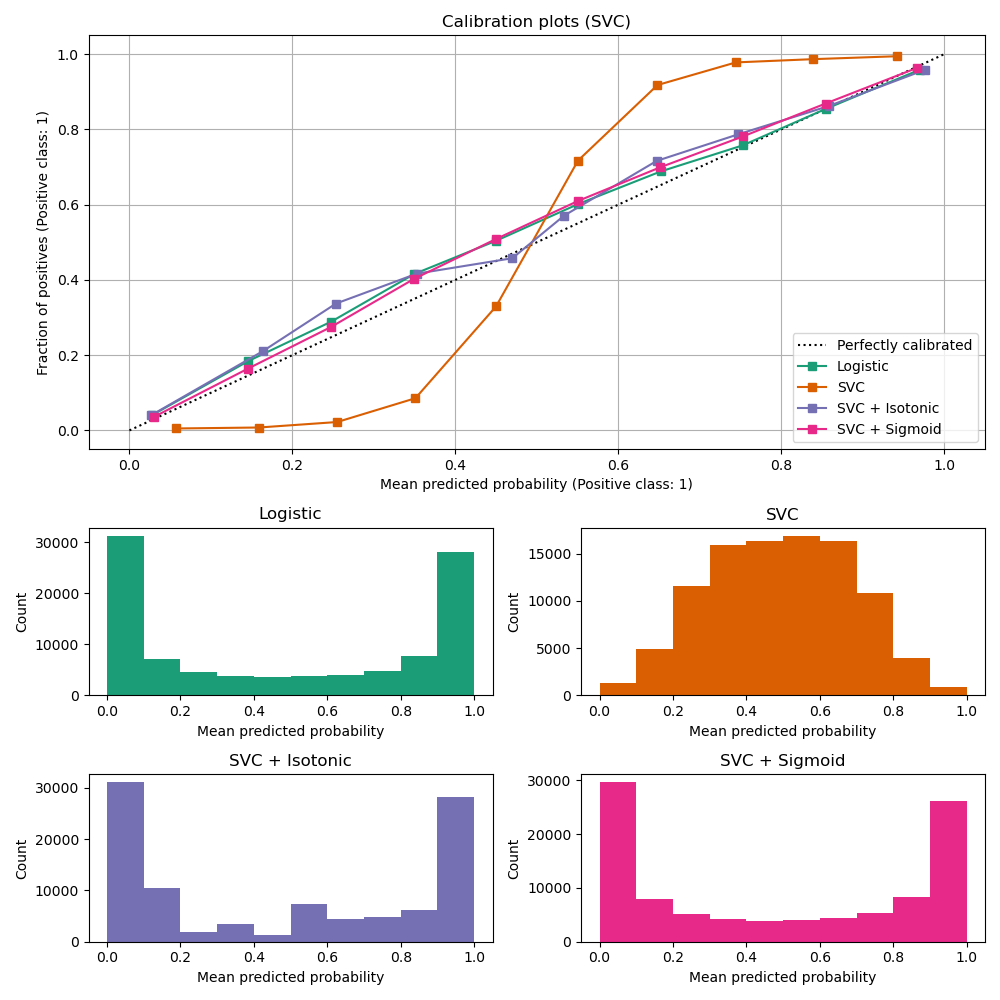
LinearSVC показывает противоположное поведение по сравнению с GaussianNB; калибровочная
кривая имеет сигмоидную форму, что типично для недостаточно уверенного
классификатора. В случае LinearSVC, это вызвано свойством запаса функции потерь hinge, которая фокусируется на образцах, близких к границе решения (опорным векторам). Образцы, далёкие от границы решения, не влияют на потерю hinge. Таким образом, логично, что LinearSVC не пытается разделить выборки в регионах с высокой уверенностью. Это приводит к более плоским калибровочным кривым около 0 и 1 и эмпирически показано на различных наборах данных в Niculescu-Mizil & Caruana [1].
Оба вида калибровки (сигмоидная и изотоническая) могут исправить эту проблему и дать схожие результаты.
Как и раньше, мы показываем Потеря по шкале Брайера, Логарифмическая потеря, точность, полнота, F1-мера и ROC AUC.
scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)
y_pred = clf.predict(X_test)
scores["Classifier"].append(name)
for metric in [brier_score_loss, log_loss, roc_auc_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_prob[:, 1]))
for metric in [precision_score, recall_score, f1_score]:
score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
scores[score_name].append(metric(y_test, y_pred))
score_df = pd.DataFrame(scores).set_index("Classifier")
score_df.round(decimals=3)
score_df
Как и с GaussianNB выше, калибровка улучшает как Потеря по шкале Брайера и Логарифмическая потеря но не сильно изменяет
метрики точности предсказания (precision, recall и F1 score).
Сводка#
Параметрическая сигмоидальная калибровка может работать с ситуациями, когда калибровочная кривая базового классификатора является сигмоидальной (например, для
LinearSVC), но не там, где он транспонированно-сигмоидальный (например, GaussianNB). Непараметрическая
изотоническая калибровка может справиться с обеими ситуациями, но может потребовать больше
данных для получения хороших результатов.
Ссылки#
Общее время выполнения скрипта: (0 минут 2.562 секунды)
Связанные примеры
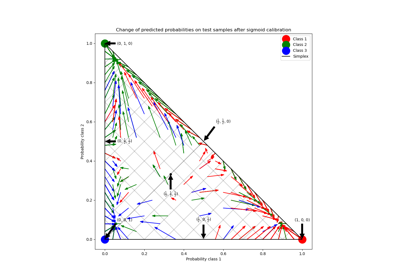
Калибровка вероятностей для классификации на 3 класса