Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Робастная оценка ковариации и релевантность расстояний Махаланобиса#

Этот пример показывает оценку ковариации с расстояниями Махаланобиса на данных с гауссовским распределением.

Для данных, распределенных по Гауссу, расстояние наблюдения \(x_i\) к моде распределения можно вычислить с использованием расстояния Махаланобиса:

\[d_{(\mu,\Sigma)}(x_i)^2 = (x_i - \mu)^T\Sigma^{-1}(x_i - \mu)\]

где \(\mu\) и \(\Sigma\) являются местоположением и ковариацией лежащих в основе распределений Гаусса.

На практике, \(\mu\) и \(\Sigma\) заменяются некоторыми оценками. Стандартная оценка максимального правдоподобия (MLE) для ковариации очень чувствительна к наличию выбросов в наборе данных, и, следовательно, последующие расстояния Махаланобиса также. Лучше использовать устойчивый оценщик ковариации, чтобы гарантировать, что оценка устойчива к "ошибочным" наблюдениям в наборе данных и что рассчитанные расстояния Махаланобиса точно отражают истинную организацию наблюдений.

Оценщик Minimum Covariance Determinant (MCD) является устойчивым, с высокой точкой разрыва (т.е. его можно использовать для оценки ковариационной матрицы сильно загрязнённых наборов данных, до \(\frac{n_\text{samples}-n_\text{features}-1}{2}\) выбросов) estimator ковариации. Идея MCD заключается в том, чтобы найти \(\frac{n_\text{samples}+n_\text{features}+1}{2}\) наблюдения, эмпирическая ковариация которых имеет наименьший определитель, что дает «чистое» подмножество наблюдений, из которого можно вычислить стандартные оценки местоположения и ковариации. MCD был введен П.Ж.Руссеу в [1].

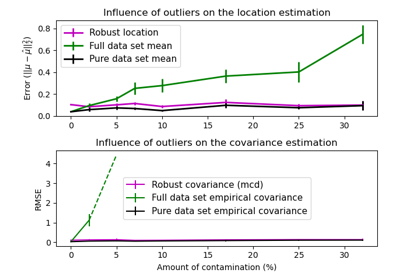
Этот пример иллюстрирует, как расстояния Махаланобиса подвержены влиянию выбросов. Наблюдения, взятые из загрязняющего распределения, неотличимы от наблюдений, полученных из реального гауссовского распределения, при использовании расстояний Махаланобиса на основе ММП-оценки ковариации. При использовании расстояний Махаланобиса на основе MCD две популяции становятся различимыми. Связанные приложения включают обнаружение выбросов, ранжирование наблюдений и кластеризацию.

Примечание

Ссылки

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Сгенерировать данные#

Сначала мы генерируем набор данных из 125 образцов и 2 признаков. Оба признака распределены по Гауссу со средним значением 0, но признак 1 имеет стандартное отклонение, равное 2, а признак 2 имеет стандартное отклонение, равное 1. Затем 25 образцов заменяются выбросами с гауссовым распределением, где признак 1 имеет стандартное отклонение, равное 1, а признак 2 имеет стандартное отклонение, равное 7.

import numpy as np

# for consistent results
np.random.seed(7)

n_samples = 125
n_outliers = 25
n_features = 2

# generate Gaussian data of shape (125, 2)
gen_cov = np.eye(n_features)
gen_cov[0, 0] = 2.0
X = np.dot(np.random.randn(n_samples, n_features), gen_cov)
# add some outliers
outliers_cov = np.eye(n_features)
outliers_cov[np.arange(1, n_features), np.arange(1, n_features)] = 7.0
X[-n_outliers:] = np.dot(np.random.randn(n_outliers, n_features), outliers_cov)

Сравнение результатов#

Ниже мы подгоняем к нашим данным ковариационные оценки на основе MCD и MLE и выводим оцененные ковариационные матрицы. Обратите внимание, что оцененная дисперсия признака 2 значительно выше с оценщиком на основе MLE (7.5), чем с робастным оценщиком MCD (1.2). Это показывает, что робастный оценщик на основе MCD гораздо более устойчив к выбросам, которые были специально созданы с гораздо большей дисперсией в признаке 2.

import matplotlib.pyplot as plt

from sklearn.covariance import EmpiricalCovariance, MinCovDet

# fit a MCD robust estimator to data
robust_cov = MinCovDet().fit(X)
# fit a MLE estimator to data
emp_cov = EmpiricalCovariance().fit(X)
print(
    "Estimated covariance matrix:\nMCD (Robust):\n{}\nMLE:\n{}".format(
        robust_cov.covariance_, emp_cov.covariance_
    )
)

Estimated covariance matrix:
MCD (Robust):
[[ 3.60075119 -0.07640781]
 [-0.07640781  1.51855963]]
MLE:
[[ 3.23773583 -0.24640578]
 [-0.24640578  7.51963999]]

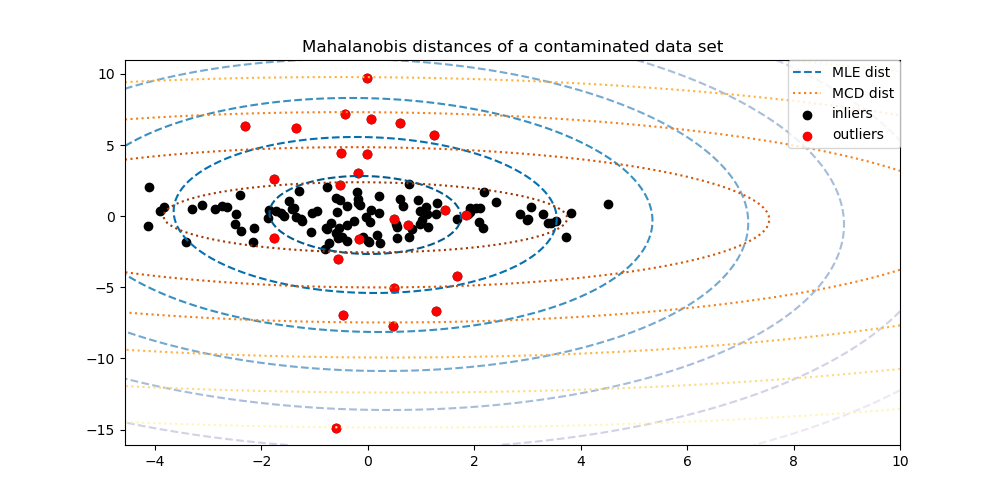
Чтобы лучше визуализировать разницу, мы строим контуры расстояний Махаланобиса, рассчитанных обоими методами. Заметьте, что устойчивые расстояния Махаланобиса на основе MCD гораздо лучше соответствуют чёрным точкам-выбросам, тогда как расстояния на основе MLE больше подвержены влиянию красных точек-выбросов.

import matplotlib.lines as mlines

fig, ax = plt.subplots(figsize=(10, 5))
# Plot data set
inlier_plot = ax.scatter(X[:, 0], X[:, 1], color="black", label="inliers")
outlier_plot = ax.scatter(
    X[:, 0][-n_outliers:], X[:, 1][-n_outliers:], color="red", label="outliers"
)
ax.set_xlim(ax.get_xlim()[0], 10.0)
ax.set_title("Mahalanobis distances of a contaminated data set")

# Create meshgrid of feature 1 and feature 2 values
xx, yy = np.meshgrid(
    np.linspace(plt.xlim()[0], plt.xlim()[1], 100),
    np.linspace(plt.ylim()[0], plt.ylim()[1], 100),
)
zz = np.c_[xx.ravel(), yy.ravel()]
# Calculate the MLE based Mahalanobis distances of the meshgrid
mahal_emp_cov = emp_cov.mahalanobis(zz)
mahal_emp_cov = mahal_emp_cov.reshape(xx.shape)
emp_cov_contour = plt.contour(
    xx, yy, np.sqrt(mahal_emp_cov), cmap=plt.cm.PuBu_r, linestyles="dashed"
)
# Calculate the MCD based Mahalanobis distances
mahal_robust_cov = robust_cov.mahalanobis(zz)
mahal_robust_cov = mahal_robust_cov.reshape(xx.shape)
robust_contour = ax.contour(
    xx, yy, np.sqrt(mahal_robust_cov), cmap=plt.cm.YlOrBr_r, linestyles="dotted"
)

# Add legend
ax.legend(
    [
        mlines.Line2D([], [], color="tab:blue", linestyle="dashed"),
        mlines.Line2D([], [], color="tab:orange", linestyle="dotted"),
        inlier_plot,
        outlier_plot,
    ],
    ["MLE dist", "MCD dist", "inliers", "outliers"],
    loc="upper right",
    borderaxespad=0,
)

plt.show()

Mahalanobis distances of a contaminated data set

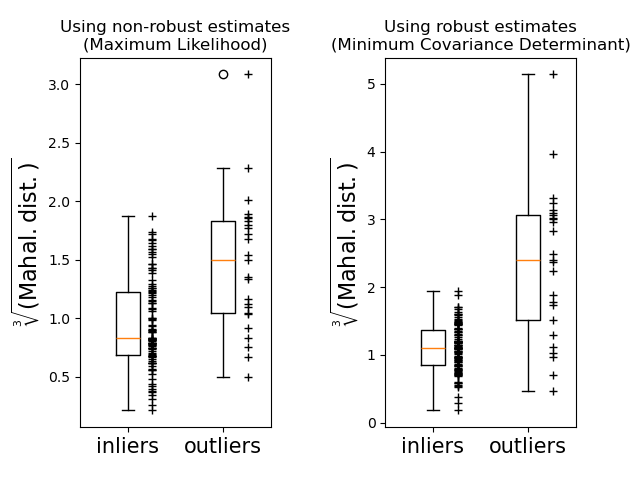
Наконец, мы подчеркиваем способность расстояний Махаланобиса на основе MCD различать выбросы. Мы извлекаем кубический корень из расстояний Махаланобиса, получая приблизительно нормальные распределения (как предложили Уилсон и Хилферти [2]), затем постройте значения выбросов и невыбросов с помощью ящичковых диаграмм. Распределение выбросов более отделено от распределения невыбросов для робастных расстояний Махаланобиса на основе MCD.

fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=0.6)

# Calculate cubic root of MLE Mahalanobis distances for samples
emp_mahal = emp_cov.mahalanobis(X - np.mean(X, 0)) ** (0.33)
# Plot boxplots
ax1.boxplot([emp_mahal[:-n_outliers], emp_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax1.plot(
    np.full(n_samples - n_outliers, 1.26),
    emp_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax1.plot(np.full(n_outliers, 2.26), emp_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax1.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax1.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax1.set_title("Using non-robust estimates\n(Maximum Likelihood)")

# Calculate cubic root of MCD Mahalanobis distances for samples
robust_mahal = robust_cov.mahalanobis(X - robust_cov.location_) ** (0.33)
# Plot boxplots
ax2.boxplot([robust_mahal[:-n_outliers], robust_mahal[-n_outliers:]], widths=0.25)
# Plot individual samples
ax2.plot(
    np.full(n_samples - n_outliers, 1.26),
    robust_mahal[:-n_outliers],
    "+k",
    markeredgewidth=1,
)
ax2.plot(np.full(n_outliers, 2.26), robust_mahal[-n_outliers:], "+k", markeredgewidth=1)
ax2.axes.set_xticklabels(("inliers", "outliers"), size=15)
ax2.set_ylabel(r"$\sqrt[3]{\rm{(Mahal. dist.)}}$", size=16)
ax2.set_title("Using robust estimates\n(Minimum Covariance Determinant)")

plt.show()