Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
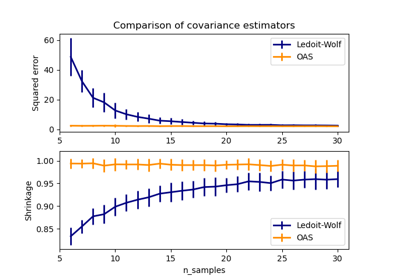
Оценка ковариации сжатием: LedoitWolf vs OAS и максимальное правдоподобие#
При работе с оценкой ковариации обычный подход заключается в использовании
оценки максимального правдоподобия, такой как
EmpiricalCovarianceОн является несмещённым, т.е. сходится к истинной (генеральной) ковариации при наличии большого количества наблюдений. Однако также может быть полезно его регуляризовать, чтобы уменьшить дисперсию; это, в свою очередь, вносит некоторое смещение. Этот пример иллюстрирует простую регуляризацию, используемую в
Сжатая ковариация оценщиков. В частности, он фокусируется на том, как
установить степень регуляризации, т.е. как выбрать компромисс между
смещением и дисперсией.
Ссылки
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Сгенерировать тестовые данные#
import numpy as np
n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))
# Color samples
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)
Вычислить правдоподобие на тестовых данных#
from scipy import linalg
from sklearn.covariance import ShrunkCovariance, empirical_covariance, log_likelihood
# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [
-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test) for s in shrinkages
]
# under the ground-truth model, which we would not have access to in real
# settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))
Сравнение различных подходов к установке параметра регуляризации#
Здесь мы сравниваем 3 подхода:
Установка параметра путем кросс-валидации правдоподобия на трех фолдах в соответствии с сеткой потенциальных параметров сжатия.
Закрытая формула, предложенная Ледойтом и Вольфом для вычисления асимптотически оптимального параметра регуляризации (минимизирующего критерий MSE), дающая
LedoitWolfоценка ковариации.Улучшение сжатия Ледойта-Вольфа,
OAS, предложенный Ченом и др. [1]. Его сходимость значительно лучше в предположении, что данные имеют гауссово распределение, особенно для малых выборок.
from sklearn.covariance import OAS, LedoitWolf
from sklearn.model_selection import GridSearchCV
# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{"shrinkage": shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)
# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)
# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)
Построить результаты#
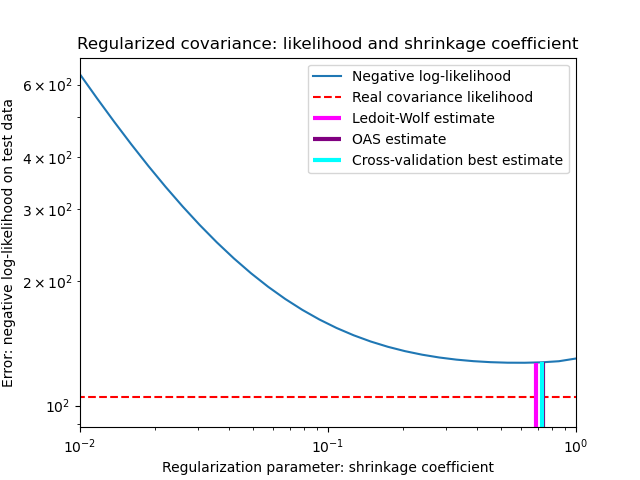
Чтобы количественно оценить ошибку оценки, мы строим график правдоподобия невидимых данных для различных значений параметра сжатия. Мы также показываем выбор с помощью перекрестной проверки или с оценками LedoitWolf и OAS.
import matplotlib.pyplot as plt
fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel("Regularization parameter: shrinkage coefficient")
plt.ylabel("Error: negative log-likelihood on test data")
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")
plt.plot(plt.xlim(), 2 * [loglik_real], "--r", label="Real covariance likelihood")
# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6.0 * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10.0 * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(
lw.shrinkage_,
ymin,
-loglik_lw,
color="magenta",
linewidth=3,
label="Ledoit-Wolf estimate",
)
# OAS likelihood
plt.vlines(
oa.shrinkage_, ymin, -loglik_oa, color="purple", linewidth=3, label="OAS estimate"
)
# best CV estimator likelihood
plt.vlines(
cv.best_estimator_.shrinkage,
ymin,
-cv.best_estimator_.score(X_test),
color="cyan",
linewidth=3,
label="Cross-validation best estimate",
)
plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()
plt.show()
Примечание
Оценка максимального правдоподобия соответствует отсутствию сжатия и поэтому работает плохо. Оценка Ледойта-Вольфа работает действительно хорошо, так как она близка к оптимальной и не требует больших вычислительных затрат. В этом примере оценка OAS находится немного дальше. Интересно, что оба подхода превосходят перекрестную проверку, которая требует значительно больших вычислительных затрат.
Общее время выполнения скрипта: (0 минут 0.402 секунды)
Связанные примеры
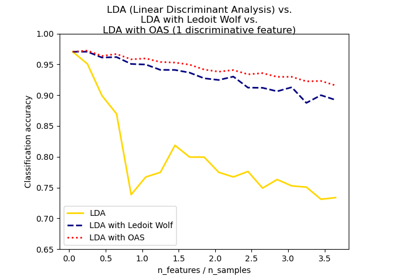
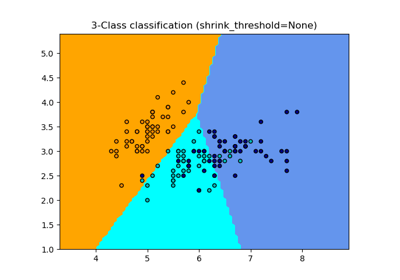
Нормальный, Ledoit-Wolf и OAS линейный дискриминантный анализ для классификации