Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Оценка разреженной обратной ковариации#
Использование оценщика GraphicalLasso для обучения ковариации и разреженной точности из небольшого числа выборок.
Для оценки вероятностной модели (например, гауссовской модели) оценка матрицы точности, то есть обратной матрицы ковариации, так же важна, как и оценка матрицы ковариации. Действительно, гауссовская модель параметризуется матрицей точности.
Чтобы быть в благоприятных условиях восстановления, мы сэмплируем данные из модели с разреженной обратной ковариационной матрицей. Кроме того, мы обеспечиваем, чтобы данные не были слишком коррелированы (ограничивая наибольший коэффициент матрицы точности) и чтобы не было малых коэффициентов в матрице точности, которые невозможно восстановить. Кроме того, при небольшом количестве наблюдений легче восстановить корреляционную матрицу, а не ковариационную, поэтому мы масштабируем временные ряды.
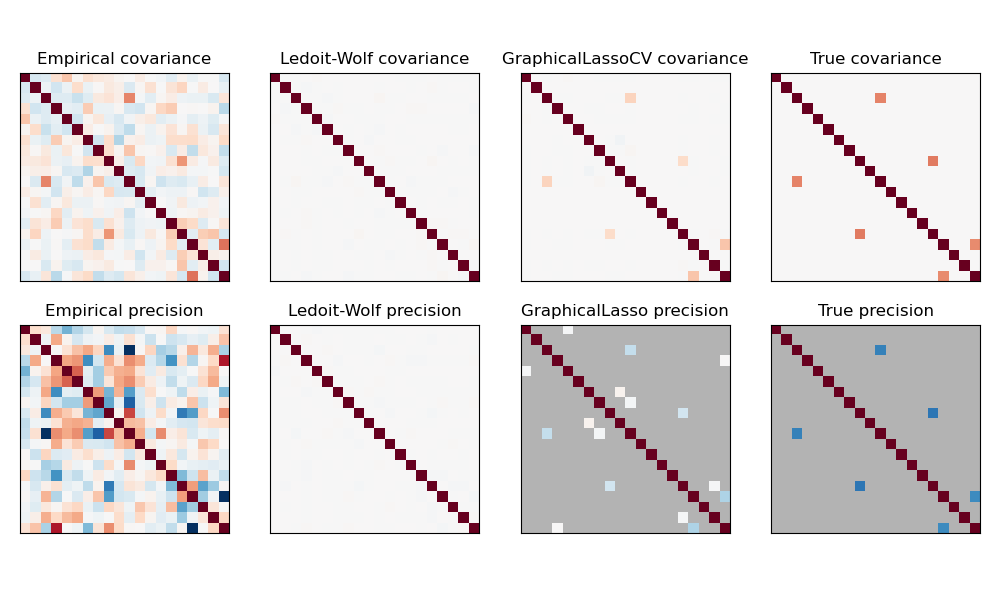
Здесь количество образцов немного больше количества измерений, поэтому эмпирическая ковариация всё ещё обратима. Однако, поскольку наблюдения сильно коррелированы, эмпирическая матрица ковариации плохо обусловлена, и в результате её обратная — эмпирическая матрица точности — сильно отличается от истинной.
Если мы используем l2-сжатие, как в оценщике Ледойта-Вольфа, то при малом количестве образцов нам нужно сильно сжимать. В результате точность Ледойта-Вольфа довольно близка к истинной точности, которая недалека от диагональной, но внедиагональная структура теряется.
Оценщик с L1-штрафом может восстановить часть этой внедиагональной структуры. Он изучает разреженную точность. Он не способен восстановить точный шаблон разреженности: он обнаруживает слишком много ненулевых коэффициентов. Однако самые высокие ненулевые коэффициенты L1 оценки соответствуют ненулевым коэффициентам в истинном распределении. Наконец, коэффициенты L1 оценки точности смещены в сторону нуля: из-за штрафа они все меньше, чем соответствующие значения истинного распределения, как видно на рисунке.
Обратите внимание, что диапазон цветов матриц точности настроен для улучшения читаемости рисунка. Полный диапазон значений эмпирической точности не отображается.
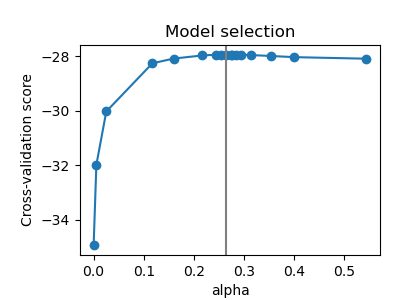
Параметр alpha в GraphicalLasso, задающий разреженность модели, устанавливается внутренней кросс-валидацией в GraphicalLassoCV. Как можно увидеть на рисунке 2, сетка для вычисления оценки кросс-валидации итеративно уточняется в окрестности максимума.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Сгенерировать данные#
import numpy as np
from scipy import linalg
from sklearn.datasets import make_sparse_spd_matrix
n_samples = 60
n_features = 20
prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(
n_features, alpha=0.98, smallest_coef=0.4, largest_coef=0.7, random_state=prng
)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)
Оценить ковариацию#
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf
emp_cov = np.dot(X.T, X) / n_samples
model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_
lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)
Построить график результатов#
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)
# plot the covariances
covs = [
("Empirical", emp_cov),
("Ledoit-Wolf", lw_cov_),
("GraphicalLassoCV", cov_),
("True", cov),
]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
plt.subplot(2, 4, i + 1)
plt.imshow(
this_cov, interpolation="nearest", vmin=-vmax, vmax=vmax, cmap=plt.cm.RdBu_r
)
plt.xticks(())
plt.yticks(())
plt.title("%s covariance" % name)
# plot the precisions
precs = [
("Empirical", linalg.inv(emp_cov)),
("Ledoit-Wolf", lw_prec_),
("GraphicalLasso", prec_),
("True", prec),
]
vmax = 0.9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
ax = plt.subplot(2, 4, i + 5)
plt.imshow(
np.ma.masked_equal(this_prec, 0),
interpolation="nearest",
vmin=-vmax,
vmax=vmax,
cmap=plt.cm.RdBu_r,
)
plt.xticks(())
plt.yticks(())
plt.title("%s precision" % name)
if hasattr(ax, "set_facecolor"):
ax.set_facecolor(".7")
else:
ax.set_axis_bgcolor(".7")
# plot the model selection metric
plt.figure(figsize=(4, 3))
plt.axes([0.2, 0.15, 0.75, 0.7])
plt.plot(model.cv_results_["alphas"], model.cv_results_["mean_test_score"], "o-")
plt.axvline(model.alpha_, color=".5")
plt.title("Model selection")
plt.ylabel("Cross-validation score")
plt.xlabel("alpha")
plt.show()
Общее время выполнения скрипта: (0 минут 0.581 секунды)
Связанные примеры
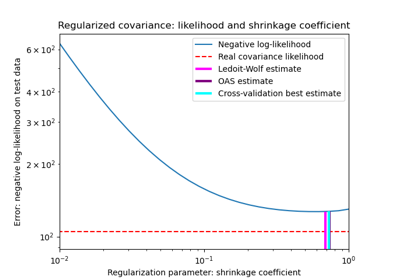
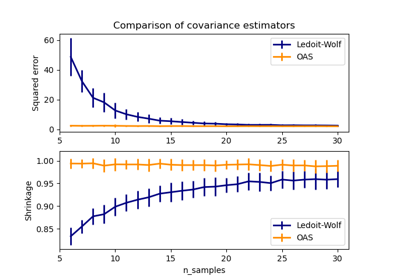
Оценка ковариации сжатием: LedoitWolf vs OAS и максимальное правдоподобие
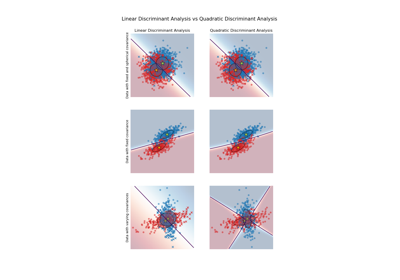
Линейный и квадратичный дискриминантный анализ с эллипсоидом ковариации