Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Снижение размерности Swiss Roll и Swiss-Hole#

Эта записная книжка стремится сравнить две популярные нелинейные техники снижения размерности, стохастическое вложение соседей с t-распределением (t-SNE) и локально линейное вложение (LLE), на классическом наборе данных Swiss Roll. Затем мы исследуем, как они обе справляются с добавлением отверстия в данных.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Швейцарский рулет#

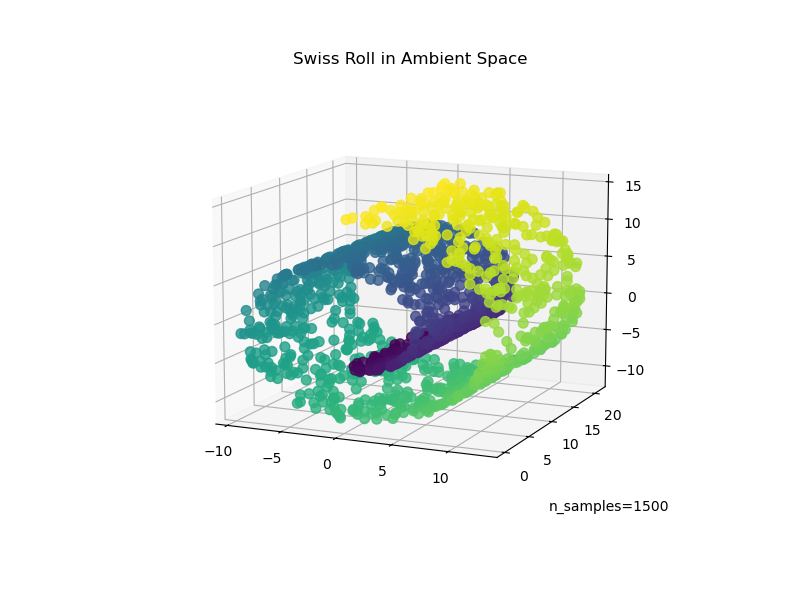
Начнем с генерации набора данных Swiss Roll.

import matplotlib.pyplot as plt

from sklearn import datasets, manifold

sr_points, sr_color = datasets.make_swiss_roll(n_samples=1500, random_state=0)

Теперь давайте посмотрим на наши данные:

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sr_points[:, 0], sr_points[:, 1], sr_points[:, 2], c=sr_color, s=50, alpha=0.8
)
ax.set_title("Swiss Roll in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

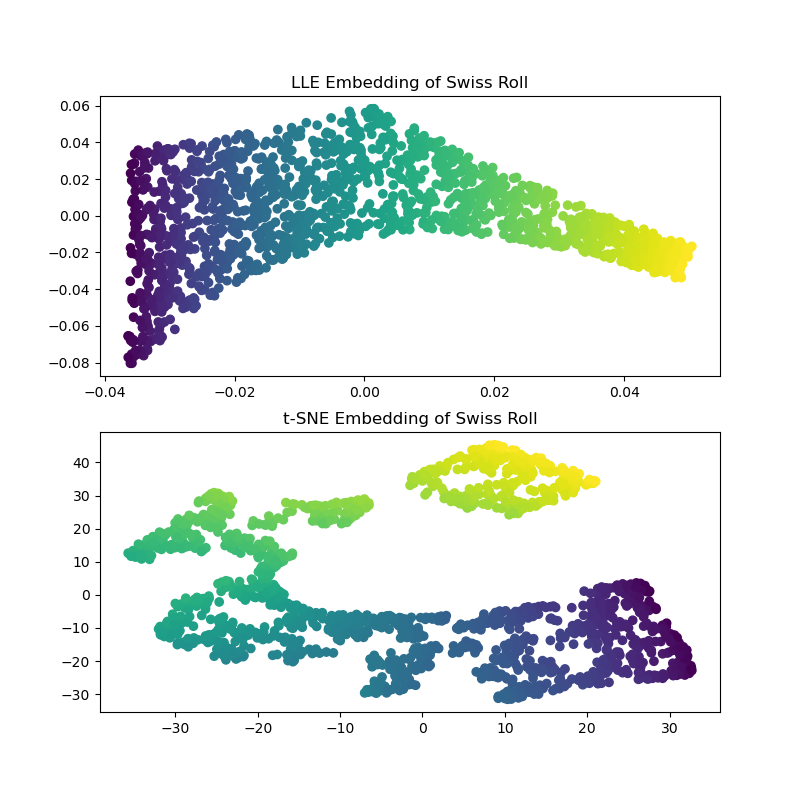
Вычисляя вложения LLE и t-SNE, мы обнаруживаем, что LLE, кажется, довольно эффективно разворачивает Швейцарский рулет. t-SNE, с другой стороны, способен сохранить общую структуру данных, но плохо представляет непрерывную природу наших исходных данных. Вместо этого он, кажется, ненужным образом собирает участки точек вместе.

sr_lle, sr_err = manifold.locally_linear_embedding(
    sr_points, n_neighbors=12, n_components=2
)

sr_tsne = manifold.TSNE(n_components=2, perplexity=40, random_state=0).fit_transform(
    sr_points
)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sr_lle[:, 0], sr_lle[:, 1], c=sr_color)
axs[0].set_title("LLE Embedding of Swiss Roll")
axs[1].scatter(sr_tsne[:, 0], sr_tsne[:, 1], c=sr_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss Roll")

LLE Embedding of Swiss Roll, t-SNE Embedding of Swiss Roll

Примечание

LLE, кажется, растягивает точки от центра (фиолетового) швейцарского рулета. Однако мы наблюдаем, что это просто побочный продукт того, как были сгенерированы данные. Существует более высокая плотность точек около центра рулета, что в конечном итоге влияет на то, как LLE восстанавливает данные в более низком измерении.

Swiss-Hole#

Теперь давайте посмотрим, как оба алгоритма справляются с добавлением отверстия в данные. Сначала мы генерируем набор данных Swiss-Hole и строим его график:

sh_points, sh_color = datasets.make_swiss_roll(
    n_samples=1500, hole=True, random_state=0
)

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
fig.add_axes(ax)
ax.scatter(
    sh_points[:, 0], sh_points[:, 1], sh_points[:, 2], c=sh_color, s=50, alpha=0.8
)
ax.set_title("Swiss-Hole in Ambient Space")
ax.view_init(azim=-66, elev=12)
_ = ax.text2D(0.8, 0.05, s="n_samples=1500", transform=ax.transAxes)

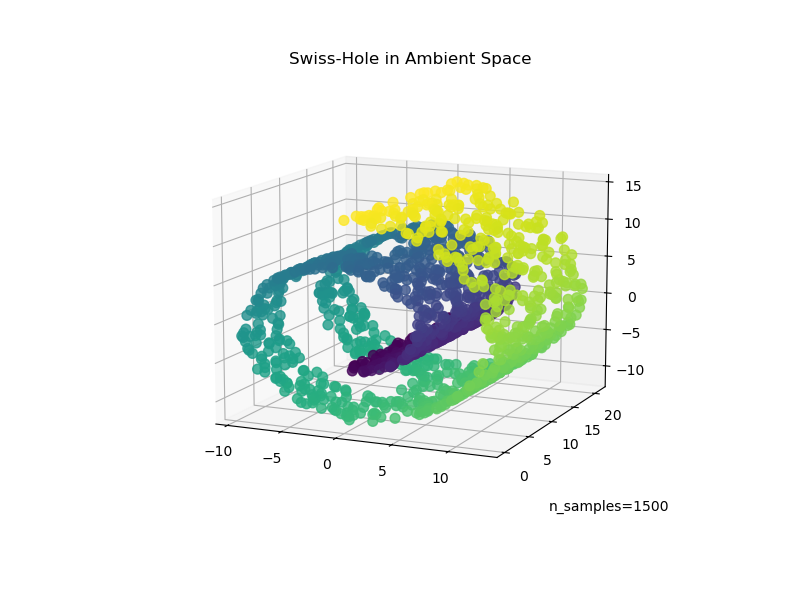
Вычисляя вложения LLE и t-SNE, мы получаем результаты, аналогичные Швейцарскому рулету. LLE очень способно разворачивает данные и даже сохраняет отверстие. t-SNE, опять же, кажется, группирует участки точек вместе, но мы отмечаем, что он сохраняет общую топологию исходных данных.

sh_lle, sh_err = manifold.locally_linear_embedding(
    sh_points, n_neighbors=12, n_components=2
)

sh_tsne = manifold.TSNE(
    n_components=2, perplexity=40, init="random", random_state=0
).fit_transform(sh_points)

fig, axs = plt.subplots(figsize=(8, 8), nrows=2)
axs[0].scatter(sh_lle[:, 0], sh_lle[:, 1], c=sh_color)
axs[0].set_title("LLE Embedding of Swiss-Hole")
axs[1].scatter(sh_tsne[:, 0], sh_tsne[:, 1], c=sh_color)
_ = axs[1].set_title("t-SNE Embedding of Swiss-Hole")

LLE Embedding of Swiss-Hole, t-SNE Embedding of Swiss-Hole

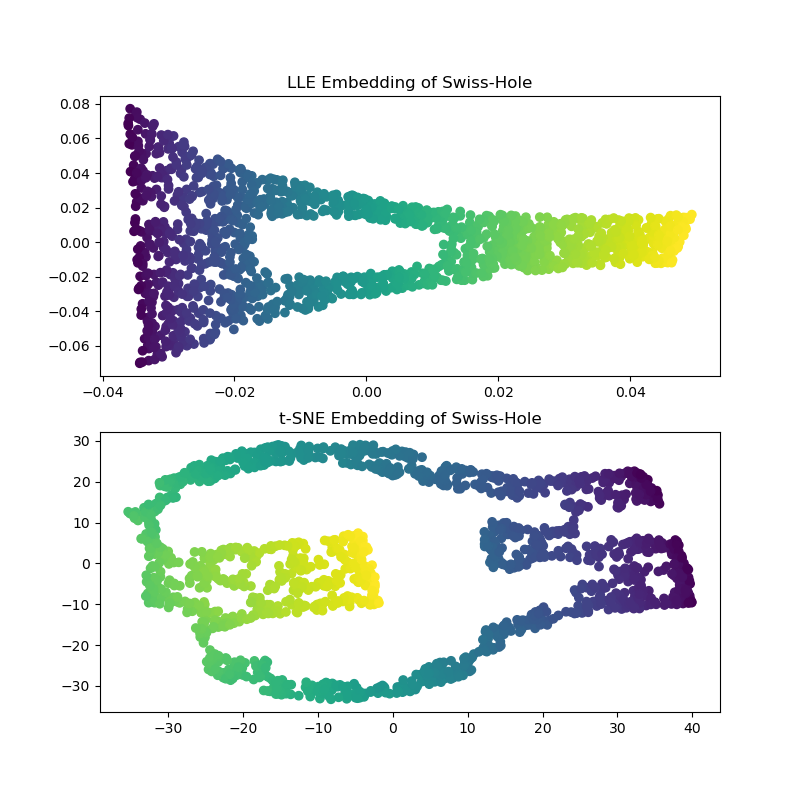
Заключительные замечания#

Отмечаем, что t-SNE выигрывает от тестирования большего количества комбинаций параметров. Лучшие результаты, вероятно, могли бы быть получены путем лучшей настройки этих параметров.

Мы наблюдаем, что, как видно в примере "Обучение многообразий на рукописных цифрах", t-SNE обычно работает лучше, чем LLE на реальных данных.

Общее время выполнения скрипта: (0 минут 18.346 секунд)